|
تضامنًا مع حق الشعب الفلسطيني |
دائرة
دائرة
|
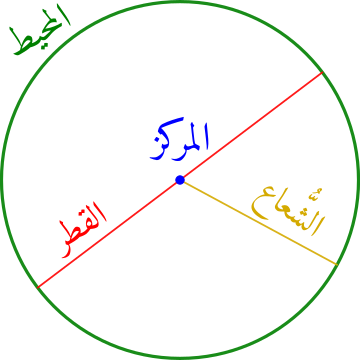
في الهَندسِةِ الرّياضِيّةِ، الدَّائرَة هي شكلٌ هَندَسيٌّ مُستوٍ، تُعرَّفُ على أنّها المحلُّ الهندسيُّ لنقاطِ تقع على سطح مُستوٍ وتَبعدُ بُعداً ثابتاً من نقطةٍ ما.[ملاحظة 1][ِ 1][ِ 2][ِ 3] تُسمَّى هَذه المجمُوعةُ غَيرُ المُنتَهيةِ من النقاطِ مُحيط الدائرةِ أو «المُحيطُ» اختصاراً. بينما النُّقطةُ الثابتةُ تُسمَّى مركزَ الدائرةِ. وأخيراً، تُسمّى المَسافةُ من أيِّ نُقطَةٍ على المُحيطِ إلى المركزِ نصفَ قُطْرِ أو شعاعاً، والقطرُ هو قِطعةٌ مُستقيمةٌ تمرُ بمركز الدائرة وتصل بين نقطتين على المحيط. تُصنُّفُ الدائرةُ على أنَّها قطعٌ ناقصٌ تلاشت بؤرتاهُ في نُقطةٍ واحدة أو قطع مخروطي مُنعدِمُ الاختلافِ المركزيّ؛ وعلى ذلك، فإنَّ الدائرةَ قطعٌ مخروطيٌّ ينتج عن تقاطع المخروط مع مستوىً مُوازٍ لقاعدتهِ. كما عُرِّفتِ الدائرةُ بوصفها مُضلَّعاً مُنتظماً لانهائي الأضلاع.[ِ 4][1][2]
ارتبطتِ الدائرةُ قديماً بالعديدِ منِ المسائل الرياضية، كما أنَّ لها ارتباطاً وثيقاً ببقيةِ الأشكالِ الهندسيّةِ من الزوايا والقطعِ المستقيمةِ والمُضلّعاتِ. يُطلق على المُضلعات التي توجَدُ دائرةٌ تُحيطها صفة «الدائرية»، أي أنَّ رؤوسَها مُشتَرِكَةٌ بِدَائِرَةٍ. ولهذهِ المُضلعاتُ قوانينُ ومبرهناتٌ خاصّةٌ تنطبق عليها. كانت الدائرةُ محطَّ اهتمامٍ بالأخصِّ عِندَ الإغريقِ القدماء. يَنتُجُ عن قِسْمَةِ طولِ مُحيطِ الدّائرةِ على طولِ قطرِها الثّابت الرّياضي أو ط. وقد ابتكر أَرْخَمِيدِس طريقةً لتقريبِ قيمة عبر حصر الدائرة بين مُضلّعين[3] وحَاوَلَ -في مسألةٍ عُرفَت بمسألة «تربيع الدائرة»- تَحويلَ الدّائرةِ إلى مربعٍ ذي المِساحَةِ ذاتها باستِعْمالِ فِرْجَارٍ ومَسطَرَةٍ فقطْ ولكنّه فشلَ في ذلك.[4] قاسَ أبولونيوس وغياث الدين الكاشي قيمة بدقةٍ عاليةٍ.[5] وحَاولَ المَصريُّونَ القُدماءُ والبابليّون إيجادَ مساحةِ الدائرةِ. تُحسَبُ مساحةُ الدائرةِ بضرب في مُربَّعِ نصف قطرها. وتختصُّ الدائرةُ عن غيرها من الأشكال الهندسية الأخرى بأنَّ لها أكبر مساحةٍ بالنِّسبةِ لطولِ مُحيطِها.[6]
وضع فلاسفة الأغريق القدماء نموذج مركزية الأرض الذي استندوا فيه على أنَّ الأرض كرةٌ تقع في مركز الكونِ والسماوات وتدور حولها بقية الأجرام السماوية في دوائرَ. وعندما قدَّم نيكولاس كوبرنيكوس نظرية مركزية الشمس، اعتبر أن نسيج الكون يتكون من حلقات دائرية حول الشمس. إلى أن توصَّلَ كيبلر إلى حقيقة شكل مدارات الأجرام السماوية، وهي قطوع ناقصة بدلاً من كونها دوائرَ، وحدد نيوتن الشروط التي يجب أن تتوفر في الجسم حتى يحذو مساراً دائرياً.[7][8]
تُعتبرُ الدائرةُ أحد أكملِ الأشكال الهندسية وأكثرها مثاليةً، وكان لها أهميَّة في التقنية والفنون والأديان والثقافات.[9][ِ 5] تُرسَمُ الدوائرَ باستعمال الفرجار. والفرجار هو الأداة الوحيدة إلى جانب المسطرة المسموح باستخدامها في الهندسة الإقليدية؛ وهذا ما جعلها تُسمَّى «هندسة المسطرة والفرجار».[10][11] تربيع الدائرة، تثليث الزاوية ومضاعفة المُكعَّب كانت من أبرز المسائل الرياضية والمواضيع التي حاول فيها الرياضيون على مر التاريخ، إلى أن أثبت بيير وانتزل وفيردينوند فون ليندمان استحالة تِلكُمُ المسائل.[12]
| هذه المقالةُ جزءٌ من سلسلةِ القطوع المخروطية | |
 | |
| قطع مكافئ | |
|---|---|
| المعادلة | |
| الانحراف المركزي() | |
| البعد البؤري() | |
  | |
| قطع زائد | |
| المعادلة | |
| الانحراف المركزي () | |
| البعد البؤري() | |
  | |
| قطع ناقص | |
| المعادلة | |
| الانحراف المركزي () | |
| البعد البؤري () | |
  | |
| دائرة (حالة خاصة من القطع الناقص) | |
| المعادلة | |
| الانحراف المركزي () | |
| البعد البؤري () | |
 | |
| • • • | |
مصطلحات أساسية
| هذهِ المقالةُ مُدَعَّمةٌ بِصوَرٍ ورُسومٍ تَوضِيحيةٍ تُرافِقُ بعضَ التَّعاريفِ والمُعادلاتِ الرِِّياضيَّة. فضلاً، تأكَّد من ظُهورِ الصوَرِ. |
يُرمز للدائرة التي مركزها النقطة ونصف قطرها [ملاحظة 2] رياضيَّاً بالرموز: «» و«» أو يُكتَفى بذكر «الدائرة » للإشارة إليها.[ِ 2] ويُرمز لها في الترميز العلمي العربي بحرف «د»[ِ 4]

| ||||
|---|---|---|---|---|
| المصطلح | التّعريف | الترميز العربي | التّرميز اللاتيني | ملاحظة |
| مركز | نقطة ثابتة تبعد البعد نفسه عن جميع النقاط الواقعة على المحيط. | م | أو | [ملاحظة 3] |
| محيط | مسار المحل الهندسي لنقطة مُتحرّكة في مستوٍ تبعد بعداً ثابتاً عن المركز. | مح | [ملاحظة 4] | |
| مساحة | منطقة السطح المحصور بمحيط الدَّائرة. | م | [ملاحظة 5] | |
| نصف قطر | أو الشعاع: قطعة مستقيمة تصل بين المركز وأي نقطة واقعة على المحيط. | نق | [ملاحظة 6] | |
| وتر | قطعة مستقيمة تصل بين أي نقطتين على محيط الدائرة. | |||
| قطر | وتر مار بمركز الدائرة. | ق | [ملاحظة 7] | |
| الجزء | التّعريف | الرمز | صورة |
|---|---|---|---|
| قوس | جزء متّصل من محيط الدائرة. | ︵ | 
|
| قطاع | مساحة منحصرة بين نصفي قطر وقوسٍ واصلٌ بينهما. | ⌔ | |
| قطعة | مساحة منحصرة بين وتر وقوسٍ يحصره. | ⌓ | |
| قرص | مساحة تحصرها دائرة. | 
| |
| نصف قرص | مساحة منحصرة بين قطر وقوسٍ يحصره.[ملاحظة 8] |
التعريف
تعودُ تسمية وتعريفُ الدائرةِ في بعض اللغات إلى أشكال كانت في الطبيعة أو صنعها الإنسان كالخواتم، الحلقات والعجلات، بينما في اللّغة العربيّةِ، تعود لفظة «دائرة» إلى الفعل «دار» أو الجذر «د ور»، والدائرة هي ما أحاط بالشّيء وتعني أيضاً «الحلقة». جاء في لسان العرب لابن منظور: «دار الشيء، يدور دَوراً ودَوَراناً، واستدار، وأدرتُه أنا. والدهر دوَّار بالإنسان. وتدوير الشيء جعله مدوّراً، وفي الحديث: إن الزمان قد استدار كهيئته يوم خلقَ الله السموات والأرض. استدار بمعنى إذا طاف حول الشيء، وإذا عاد إلى الموضع الذي ابتدأ منه...». يضيف ابن منظور: «والدائرة والدارة كلاهما: ما أحاط بالشيء. والدارةُ: دارة القمر التي حوله، وهي الهالة. ودارت عليه الدوائر: أي نزلت به الدواهي، والدائرة: الهزيمة والسوء، يقال: عليهم دائرة السوء... والدَّوَّار والدُّوَّار من أسماء البيت الحرام، لأنهم يطوفون به في شبه دائرة...».[14][ِ 6] وفي اللّغة الإنجليزيّة يعود أصل تسمية الدائرة (بالإنجليزية: Circle) إلى الكلمة الإغريقيّة κίρκος/κύκλος (تُنطق: كيركوس/كوكلس) المُحرَّفة من الكلمة الإغريقية الهومرية κρίκος (كريكوس)، والتي تعني «الطّوق» أو«الخاتم».[15]
وفقاً لتعريف الدّائرة الذي ينصُّ على أنها مجموعة نقاط على مستوى واحد تبعد البعد ذاته عن نقطة ثابتة ما، فَيُمكِنُ إعادةُ صياغةِ التّعريفِ إلى أنَّ الدائرة هي منحنى مغلق أحادي البُعد، وبشكل مكافئ هي مُنحنى ترسمه نّقطةٌ متحرّكة تبعد بُعداً ثابتاً عن نقطة ثابتةٍ أخرى.[ملاحظة 9] وكونها كذلك فهي تقسم المستوى إلى جزأين: داخل الدائرة وخارجها. في الاستعمال اليومي المتداول، قد يستعمل مصطلح «دائرة» للإشارة إلى محيط الدائرة[16]، كما أنه قد يستعمل للإشارة إلى ما يوجد بداخل الدائرة؛ لكن في الاستعمال التّقني الدّقيق، الدائرة هي المحيط فقط ويُسمّى ما داخلها قُرصاً. غالباً ما يُفرّق الرَّياضيُّونَ بين السطح الدائري المغلق أو القرص والسطح الدائري المفتوح (يُسمّى بالدائرة الداخلية) اعتماداً على وقوع خط الدائرة في الاعتبار من عدمه.[1][17]
تعريف إقليدس
عرَّف إقليدس الدائرة في كتابه: الأصول، كما يأتي:[ِ 4]
يُعبِّرُ الرياضيون عن تعريف إقليدس للدائرة أيضاً باستخدام نظرية المجموعات على النحو الآتي:[18]
تعريف إقليدس في نظرية المجموعات — إذا وقعت النقطة على المستوى فإن الدائرة التي مركزها ونصف قطرها هي مجموعة جميع النقاط التي تنتمي إلى المستوى ، وتبعد عن النقطة مسافةً مقدارها .
- ويمكن صياغة التعريف السابق رياضيَّاً بالشكل التالي:
تعريف أبولونيوس

أثبت أبولونيوس أن الدائرة بالإمكان التعبير عنها على أنها المحل الهندسي لجميع النقاط التي نسبة بعدها عن نقطتين ثابتتين ثابتة. أو رياضياً: بفرض أنَّ نقطتين ثابتتين على المستوى، فإنَّ الدائرةَ التي بُؤرَتَيْها هي المحل الهندسي لجميع النقاط التي تُحقِّقُ أنَّ:[19][20][21]
النسبة التبادلية لدائرة
تُعرف النسبة التبادلية للقطعتين المستقيمتين أو لرباعية النقاط المتسامتة على الترتيب: حيث أنَّ النّسب نسبٌ مُوجّهةٌ. وتُعمم النسبة التبادلية لتشمل الدائرة بتعريف المستوى العقدي بالصيغة الآتية: . إذا كانت النقاط مُتسامتةً في المستوى العقدي كما الشكل، فإنَّ دائرة أبولونيوس لهذه الثلاث نقاط هي مجموعة النقاط التي تحقق أن معيار النسبة التبادلية مساوية لواحد.. بمعنىً آخر: هي نقطة على دائرة أبولونيوس للنقاط إذا وفقط إذا كان معيار النسبة التبادلية مساوياً للواحد.[22][23][24]
تُعرّفُ النقطة على أنّها المرافق التوافقي للنقطة بالنسبة لـ و. إذا كانت النسبة التوافقية للنقاط الأربع تساوي . وتُسمَّى حينئذٍ نسبةً توافقية. ونتيجةً لذلك، فإنَّ النسبة التبادلية بالإمكان اعتبارها على أنها مدى بُعدِ الأربع نقاط عن النسبة التوافقية.[25] النسبة التبادلية مُعرّفة منذ القِدَم، حيث يرجّح أن إقليدس هو أوّل من ذكرها، كما استعملها ببس الرومي الذي لاحظ خاصيّة ثباتها تحت التحويلات الخطية. فالنسبة التبادلية لأيِّ قطعةٍ مُستقيمةٍ تقطع 4 مستقيمات متلاقية هي ثابتة. بشكلٍ مُكافئ، يُعرّفُ ذلكَ في الهندسة الإسقاطية على أنَّ النسبة التبادلية ثابتةٌ تحت أي تحويلٍ خطيٍ كسريٍ.[25] في تعريفِ أبولونيوس للدائرة، تُسمَّى الخطوط «حُزمة توافقية» وهي كل مجموعة خطوط متلاقية نسبتها توافقية (أي: نسبتها التبادلية تساوي ). إنَّ نقاطَ تقاطعِ دائرةٍ مع حُزمةٍ توافقيةٍ رأسها يقع على الدائرة أيضاً يُنتجُ رباعياً توافقياً.[26]
تعريف الدائرة المعممة

في حال ما كانت منتصف القطعة فعندئذٍ يُسمّى المحل الهندسي للنقاط التي تحقق الشرط أعلاه، «دائرة مُعمّمة». الدائرة المعممة قد تكون دائرةً فعليةً وقد تكون خطاً مُستقيماً. وبهذا، فإنَّ التعريف المعمم للدائرة يضمُّ الخطَّ المستقيمَ على أنه دائرة مركزها هو نقطة في اللانهاية أو دائرة ذات نصف قطر لانهائي. وتستعمل فروع هندسة أخرى كالهندسة التعاكسية والهندسة الإسقاطية في المستوى العقدي هذا التعريف للدائرة على أنها خط مستقيم.[27][28] هُناك أيضاً إعادة تعريف للنقطة على أنَها دائرةٌ مُنعدمة. يُستعمل هذا التعريف افتراضياً في المسائل المتعلقة بالمحور الأساسي.[29][30]
تأويل لانهائي

بالإمكان تعريف الدائرة على أنها مُضلّعٌ منتظمٌ بنصف قطر مماسي (بالإنجليزية: Inradius)[ملاحظة 10] يُرمز إليه بالرمز أو نصف قطر محيطي (بالإنجليزية: Circumradius)[ملاحظة 11] يُرمز إليه بالرمز باعتبار أن عدد أضلاع المضلع المنتظم يؤول إلى اللانهاية. بناءً على هذا التعريف بالإمكان اشتقاق طول محيط المضلع عبر العلاقة الجبرية الآتية:[31] والمساحة، عبر العلاقة:[31]والنتيجتان تظهران مُتساويتين سواءً باستخدام نصف القطر المماسي أو نصف القطر المحيطي، لأن نصفي القطرين يؤولان للقيمة نفسها عند المالانهاية.[31]
الدائرة بوصفها حالة حدية
تُوصف الدائرة على أنها حالة حدية خاصة باستعمال أكثر من مُقاربةٍ رياضيةٍ: من أشهرها هي وصفها قطعاً مخروطيّاً. تُصنّف الدائرة على أنها بيضاوي ديكارتي، نسبةً إلى رينيه ديكارت، وهو منحنى مستو ومجموعة النقاط في المستوى التي لها نفس التركيب الخطي (ويُعبّر عنه أيضاً بمجموعٍ موزونٍ) بالنسبة لنقطتين ثابتتين في المستوى. وهي بذلكَ حالةٌ خاصّةٌ منه تكون عند انعدام أحد الأوزان وتؤوُّلِه للصفر.[32] البيضاوي الفائق هو مجموعة نقاط في المستوى تحقق: حيث أنَّ أعدادٌ مُوجبة. تُعرَفُ «الدّائرةُ الفائقة» على أنها بيضاوي فائق يكون فيه . والدّائرةُ هي حالةٌ خاصّة من الدائرة الفائقة تكون عندما .[33]
القطوع المخروطية
تُوصَفُ الدائرةُ باعتبارها حالةً خاصةً من القطع الناقص، حيث تكونُ حينَ تنطبقا البؤرتان معاً لِتُكوِّنَ مركزَ الدّائرةِ؛ حينئذٍ، يكون الاختلاف المركزي مُساوٍ للصفر () ويتساوى المحور الأكبر مع المحور الأصغر ليُكوِّنا قُطرَيْ الدائرةِ. وعلى الوجه المقابل فهي قطع مخروطي ينتج من تقاطع مخروط قائم مع مستوى عمودي على محوره.[31]
استيفاء المساحة
تعود مسألة المحيط الثابت إلى القِدمِ، وتصاغ كالآتي: «من بين جميعِ المُنحنياتِ المُغلَقةِ ذات مُحيطٍ مُعطىً، أيُّها يجعلُ مساحتها أكبر ما يُمكن؟» وُجِدَ أنّ هذه المسألةَ مُكافئةٌ لمسألة شبيهة: «من بين جميع المنحنيات المُغلقة ذات مساحةٍ مُعطاةٍ، أيُّها يجعلُ محيطَها أكبرُ ما يُمكن؟». وتختصُّ الدائرةُ بأنها الحل لهذا المسألة. إذ توصف على أنَّها الشكلُ الذي يحصر أكبر مساحةٍ نسبةً إلى طول مُحيطه.[34]
ترتبط هذه المسألةُ بمفهومِ مبدأِ الفعلِ الأدنى في الفيزياء، والذي بالإمكان صياغته على الصورة: ما «الفعلُ الذي يجعل المساحة أكبر ما يُمكن بأقلّ جهدٍ ممكن؟» على الرغم من أنَّ الدائرةَ كانت الحل الأوضح لهذه المسألة، إلا أنّ إثباتَ ذلكَ كان صعباً. أوّل محاولة أنَجَزَتْ في السؤالِ كانت سنة 1838م عندما استعمل المهندس الرياضياتي السويسري ياكوب شتاينر طريقةً هندسيةً أُسميَت لاحقاً بطريقةِ شتاينر للاستنظار. أثبت شتاينر أنَّه إذا وُجِدَ حلٌّ لهذه المسألةِ فلا بُدّ وأن يكون دائرةً. استئنف رياضيّون حلّ شتاينر لاحقاً وأكملوه.[35]
بدأ شتاينر بأول الإنشاءات الهندسية التي عُرفت جيداً؛ فعلى سبيلِ المثالِ، إن كان هناك منحنى مغلق ليس محدباً بالكامل، فبالإمكان إيجاد منحنى أكثر تحدباً منه وأعلى في المساحة عن طريق طَيّ الأجزاء المقعرة لجعلها محدبة. وبُرهِنَ أيضاً أن أي شكل لامتماثل بالإمكان تمديده بحيث يُغطي مساحةً أكبر. ولأن الشكل الوحيد المُحدب والمتناظر تماماً هو الدائرة فإن الحل كان لا بد وأن يكون هو. مع ذلك، هذا الحل بمفرده لا يُقدّمُ بُرهاناً صارماً للمسألة، إذ أنَّه مليءٌ بالثغرات التي تحتاج إلى المراجعة.[35]
غالباً ما يُعبّرُ عن مسألة المحيط الثابت بمتباينةٍ تربطُ طولَ منحنىً مغلقٍ بمساحته. تنص متباينة المحيط الثابت على أنَّ:[35][36]
وتحقّق المساواةُ إذا وفقط إذا كان المنحنى دائرةً. مساحة القرص ذو الشعاع هو ومُحيطُ الدائرةِ هو بِهذا فإنّ كلا الطرفين يصبحان . وُجدت عشرات البراهين المختلفة لمتباينة المحيط الثابت، ففي 1902، نَشَرَ أدولف هرفيتز بُرهاناً قصيراً باستخدام متسلسلة فورييه التي تُطبّق لأي منحنى محدود الطول حتى ولو كان مقعراً. في عام 1938م، قدّم شميت حلّاً أنيقاً للمسألةِ بناءً على مقارنةٍ بين منحنىً بسيط مغلق سَوِيٌّ مع دائرة معطاة. استخدم الحل صيغة طول القوس، صيغة مساحة السطح من مبرهنة غرين ومتباينة كاوشي شفارتز.[35] لأي منحنى مغلق، كسر المحيط المغلق يُعرف على أنه النسبة بين مساحته وبين مساحة الدائرة ذات المحيط نفسه. رياضياً:[35]
تنص متباينة ثباتية المحيط على أنَّ بالتكافؤ، فإنّ نسبة ثباتيّةُ المحيط هي على الأقل لكل منحنى.[36] أما بالنسبة للمضلعات المنتظمة النونية، فإنّ نسبة ثباتية المحيط هي:[36] . إذا كان منحنى مغلقاً محدباً سَويَّاً فإنَّ متباينة ثباتية المحيط المُطوَّرة تنص على أنَّ:[35]
حيث أن ترمز إلى طول والمساحة التي يحصرها، والمساحة المتجهة له، على الترتيب. تحقق المساواة فقط وإذا فقط كان منحنى ثابت العرض.[35]
دوائر بإعادة تعريف المسافة

تعريفُ دائرةٍ على أنها مجرد مجموعة نقاط ذات بعد ثابت عن نقطة يُؤدِّي إلى ضمّ أشكالٍ أخرى إلى هذا التعريف. تُعدّ هذه الأشكالُ دوائرَ بسبب يعود إلى تعاريفٍ مُختلفةٍ للمسافة عن التعريف الإقليدي لها المُعتاد. ففي المعيار- (بالإنجليزية: p-norm)، تُعرَّفُ المسافة بالقانون:[37][38]
بينما في الهندسة الإقليدية، وكحالةٍ خاصةٍ، تكون ، وبهذا تكون الصيغة المعروفة:[37][38]
في هندسة سيارة الأجرة، تكون . دوائر سيارة الأجرة تُعرّف على أنها مربعات مدوّرة بزاوية 45 بالنسبة إلى محاورها الإحداثية. على الوجه المقابل، فاعتماداً على تعريف المسافة الشبشفية، فإنَّ الدائرة ذات الشعاع في المستوى هي أيضاً مُربّع ذو ضلع . لكنها خلاف دائرة سيارة الأجرة، توازي المحاور الإحداثية.[37][38]
النَّتائِجُ التَّحليليَّة
يرتبط الشّعاع مع القطر بالعلاقة . يُعتبر القطر حالةً خاصةً من الوتر[ملاحظة 12] يقسم فيها الدائرة إلى جزئين متناظرين ومتطابقين. ويُوصف أيضاً على أنه أطول قطعة مستقيمة بين أي نقطتين تقعان على محيط الدائرة.[ِ 2][ِ 7][39] وتُصنّف جميعُ الدوائرَ على أنها مُتشابهة.[40]
المُحِيطُ وثَابِتُ النّسبة

| جزء من سلسلة مقالات حول |
| الثابت الرياضي π |
|---|
يتناسبُ طولُ مُحيطِ الدائرةِ مع طول قطرِها.[ملاحظة 13] ويُرمز لهذه النسبة بـ«»[ملاحظة 14] أو «ط». يُربَطُ بينَ ثابتِ النّسبة وبينَ القطرِ والمُحيطِ بالمُعادلة التّالية، مع اختلافِ بعضِ الصّيغِ المُشتّقة منها:[ِ 7][ِ 4]في مسائل الدّائرة وإيجاد المجاهيل منها، غالباً ما يُستعملُ تَقريبٌ لقيمة ، وهو مُشتَقٌّ من مُتباينة أرخميدس التي أوجدها عبر حصر مُحيط الدائرة بين مُضلَّعين. الفقرة الآتية توضح التقريبات الشّائعة لقيمة :[41]
- على الرغم من تعريف الأساسي على أنه نسبة المحيط إلى القطر، إلا أن لدى تعريفاتٍ متكافئة أخرى تظهر في العديد من الصيغ في جميع مجالات الرياضيات والفيزياء. ويُمَثلُ بالحرف اليوناني منذ منتصف القرن الثامن عشر. على الرغم من أنه يُنطَق باي، إلا أنه يسمى أيضاً ثابت أرخميدس. بسبب كونه عدداً غير نسبي، لا يمكن التعبير عنه ككسر، أي لا يمكن كتابته على صورة . بالمقابل، تمثيله العشري لا ينتهي ولا يستقر أبدًا في نمط تكراري منتظم. مع ذلك، فإن الكسور مثل 22/7 والأرقام الحقيقية الأخرى تستخدم عادة لتقريب . كما أن عدد متسامٍ؛ بمعنى أنه ليس جذراً لأي كثيرة حدود ذات معاملات حقيقية. هذه الخاصيَّة حلت المسألة القديمة المتمثلة في تربيع الدائرة باستخدام إنشاءات الفرجار والمسطرة.[42][43] في القرنين العشرين والواحد والعشرين، اكتشف علماء الرياضيات وعلماء الحاسوب مقاربات جديدة، عندما اقترنت بزيادة القدرة الحسابية، وسعت التمثيل العشري لـ إلى العديد من تريليونات من الأرقام بعد العلامة العشرية.[44][45] تعلق الثابت بالدائرة، جعله يوجد في العديد من الصيغ في علم المثلثات والهندسة، وخاصة تلك المتعلقة بالدوائر، والقطوع الناقصة، ومجالات التحليل الرياضي.
المِساحَةُ

تَتَناسبُ مِسَاحةُ الدّائرةِ طرديّاً مع مُربّع نصفِ القطرِ بثابتِ تناسبٍ يُطلق عليهِ . ومِسَاحةُ الدائرةِ هي أكبرُ مساحةٍ من بين الأشكالِ نسبةً إلى محيطها. وهذا يربِطُ الدائرةَ بِمُعْضِلَةٍ في مجالِ حسابِ التغيراتِ تُسمَّى مُتَباينةَ المُحيطِ الثَّابِتِ. استُعمل مفهوم النّهايات المُتتالية للحصول على قانون مساحة الدّائرة. وهذا المفهومُ قائمٌ على تقسيمِ قِرْصِ الدّائرةِ إلى قِطاعاتٍ ثمَّ جَمعِها. بعدَ التقسيمِ، ينتجُ مستطيلٌ طُولُه وعَرْضُه . وعلى هذا، تَكونُ مساحةُ الدّائرةِ مُكافئةً لمساحة المُستطيلِ بالقانون:[ِ 7]
الأقْواسُ
يُعبِّرُ مصطلحُ «قياس القوس» إلى قياسِ الزاويةِ المركزيةِ التي تَحصِرُ القوسَ. وباعتبار أن الدائرة قوساً مُتَّصِلَ الطَّرفَينِ فإن قياسُها بالدرجاتِ . وعلى ذلكَ، فإن قياسَ الأقواسِ الناتجةِ عنْ قَطْعِ زاويةٍ مركزيةٍ لدائرتينِ متحدتَيْ المركزِ لهُمَا القياسَ نَفْسَهُ؛ لاشتراكِهِما في قياسِ الزاويةِ المركزيةِ. ويتطابقُ قوسانِ من دائرةٍ واحدةٍ إذا وفقط إذا كان لهُما القياسَ نَفسه. وهُناكَ قياسانِ شهيرانِ للقوسِ:[ِ 2]
| الدرجة | الراديان |
|---|---|

|
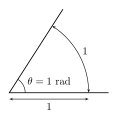
|
| يُعرَّف القوس الذي قياسه درجة واحدة على أنه من قياس الدائرة كاملةً. | يُعرَّف القوس الذي قياسه راديان واحد على أنه القوس الذي طوله نصف قطر الدائرة الأصلية . |
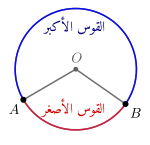
كانت
نقطتين مختلفتين على الدائرة
فإنهما يقسمان الدائرة إلى قوسين: قوس أصغر
، وقوس أكبر
يتممان بعضهما بعضاً. يُرمَز إلى القوس الأكبر
أحياناً بالرمز
عِوَضاً عن ذكر «
الأكبر». يُعرّف القوس الأصغر
على أنَّه مجموعةُ النّقاط الناتجةِ عن تقاطعِ الدائرةِ مع نقاطِ الزاويةِ المركزية
الداخلية[ملاحظة 15] ويُعبَّرُ عنه أيضاً بأنه القوس الأقصر طولاً الذي يصل بين النقطتين
على الدَّائرة، حيثُ يُساوي قياسه قياسَ الزَّاويةِ المركزيةِ المُقابلةِ لَهُ، ويقل عن
. على الوجه المقابل، فإن القوس الأكبر
هو مجموعةُ النّقاط الناتجةِ عن تقاطعِ الدائرةِ مع نقاطِ الزاويةِ المركزية
المُنعكِسة ويُعبَّرُ عنه أيضاً بأنه القوس الأقصر طولاً الذي يصل بين النقطتين
على الدَّائرة، حيثُ يُساوي قياسه قياسَ الزَّاويةِ المركزيةِ المُقابلةِ لَهُ، ويزيد عن
. تُسمَّى النقطتان
طرفا القوس
أو طرفا الوتر
. في حالِ كَوْنِ النُّقطتينِ
نقطتينِ متقابلتينِ قُطريَّاً، فإن كُلاً مِن القَوسَيْنِ المُقَابِلَيْنِ لَهُمَا القياس نفسه، ويُسمَّى القوسُ الواحدُ نِصفَ دَائرةٍ. وكُلُّ قِطْرٍ في دائرةٍ ما يُحدِّدُ نِصفَيْ دائرةٍ.[ِ 2]
إذا كانَ طُولُ القوْسِ يُساوي ، فإنَّ النسبةَ بينَ طولِ القوسِ إلى مُحيطِ الدَّائرةِ يُساوي نسبةَ قياسِ القوسِ إلى قِياسِ الدَّائرةِ كاملةً.[13][46]
| القوس الأصغر | القوس الأكبر (أو اختصاراً ) | نصف الدَّائرة |

|
|

|
القطع والجزئيات
القرص

هو منطقة المستوى التي تحصرها الدّائرة. ويعرَّف رياضيَّاً:[ِ 2].
القطاع
يعتمد حجم قطاع الدائرة على قياس الزاوية المركزية التي يحصرها ونصف قطر الدائرة. حيث يُمثِّل القطاع نسبةً من مساحة الدّائرة الكُلّية هي نفسها نسبة قياس زاويته المركزية على قياس الدائرة الكُلّية. أي أن: مساحة القطاع مُساوية لحاصل ضرب نسبة زاويته المركزية لزاوية الدائرة الكلية في مساحة الدائرة الكُلّية.[ِ 7][47]تُستعمل القطاعات كذلك في الإحصاء لتمثيل البيانات. وبطريقةٍ مُشابهة، يُؤخذ تناسب زاوية القطاع المركزية إلى مع النسبة المئوية للبيانات، حيث تُمثّل الدائرة الكاملة في الإحصاء نسبة .[48]
الزوايا

|

|

|
|---|
| الزاوية | التّعريف | موقع رأس الزَّاوية | قياس الزَّاوية | ملاحظة |
|---|---|---|---|---|
| زاوية مركزية | زاوية محصورة بين نصفي قطرين ويُرمز لها بـ | مركز الدَّائرة | قياس القوس المقابل | [ملاحظة 16] |
| زاوية محيطية | زاوية محصورة بين وترين متلاقيين على المحيط | محيط الدَّائرة | نصف قياس القوس المقابل | [ملاحظة 17] |
| زاوية مماسية | زاوية محصورة بين مماس ووتر يمر بنقطة التماس | محيط الدائرة | نصف قياس القوس المَحصُور. | [ملاحظة 18] |
| زاوية خارجة | زاوية امتداد أحد زوايا رباعي دائري المحيطة | محيط الدائرة | قياس الزاوية المقابلة لها من الرباعي. | |
| زاوية داخلية | زاوية محصورة بين قاطعين داخل الدَّائرة | داخل الدَّائرة | نصف مجموع قياسي القوس المقابل للزاوية والقوس المقابل للزاوية التي تقابلها بالرأس | |
| زاوية خارجيَّة | زاوية محصورة بين قاطعين خارج الدَّائرة | خارج الدَّائرة | نصف الفرق المطلق بين قياسي القوسين المقابلين لها |
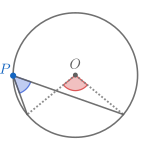
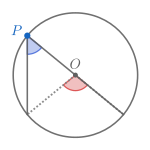
| الحالة الأولى | الحالة الثَّانية | الحالة الثَّالثة | مبرهنةُ طالس (حالة خاصَّة) |
|---|---|---|---|
|
|

|

|
| يَقَعُ مَرْكَزُ الدَّائِرَةِ خَارِجَ الزَّاويةِ المُحيطيَّةِ. | يَقَعُ مَرْكَزُ الدَّائرةِ على أحدِ ضِلْعَيْ الزَّاويةِ المُحيطيةِ. | يَقعُ مَركَزُ الدَّائرةِ دَاخلَ مَنطقةِ الزَّاوية المُحيطيَّة. | الزَّاويةُ المُحيطيةُ زَاوِيةٌ مُستقيمةٌ. |
| جزء من سلسلة مقالات حول |
| الزوايا |
|---|
 |
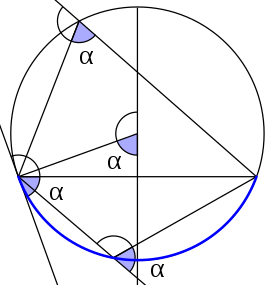
مبرهنة الزوايا المماسية والمحيطية — الزَّاويةُ المركزيةُ تُساوي ضِعفَ الزاويةِ المُحيطيةِ المُشتركةِ معها على القوسِ نفسه وضِعفَ الزاويةِ المماسية التي تحصر القوس نفسه.
المُبرهنة السابقة تُعطي علاقةً بين الزوايا المركزية وبين الزوايا المماسية والمحيطية. كنتيجة، عند تثبيت قوسٍ ما في دائرة، فإنَّ الزوايا المحيطية التي تحصر هذا القوس متساوية. والعكس صحيحٌ أيضاً، فالمحل الهندسي لرؤوس الزوايا متساوية القياسات التي تحصر قطعةً مُستقيمةً ثابتةَ الطول هي قوس دائري. وينتج عن هذه المبرهنة أيضاً مبرهنة طالس: والتي تنص على أنَّ الزاويةَ المُحيطيةَ التي تَحصِرُ قطراً قائمةٌ.[49][ِ 3][ِ 8]
مبرهنة الزاوية الداخلية — الزاوية الداخلية تُساوي نصف مجموع قياسي القوسين المَحصُورَينِ بين ضلعيها.
مبرهنة الزاوية الخارجية — الزاوية الخارجية تساوي نصف الفرق المطلق بين قياسي القوسين المحصورين بين ضلعيها.
النقاط

|
|
|---|---|
| النِّقاطُ هِيَ نِقاطٌ دَاخليةٌ ومُحيطيَّةٌ وخَارِجَةٌ على التَّرْتيبِ. | النقطتانِ نُقطَتانِ مُتقَابَلَتان قطْرياً. |
هُناك ثلاثُ حالات ممكنةٍ لموقعِ نُقطةٍ ما بالنسبةِ إلى دائرةٍ مُعطاةٍ في المستوى نَفسِهِ تُصنّفُ حَسب بُعدِها من مركز الدائرة: نقاط داخليَّة ومُحيطيَّة وخارجيَّة:[ِ 2][ِ 1]
| التصنيف | التعريف | الترميز | مراجع |
|---|---|---|---|
| نقطة داخلية | نقطة تقع داخل الدائرة، أي: تبعد عن المركز مسافةً أقل من نصف القطر. | [ملاحظة 19] | |
| نقطة مُحيطيَّة | نقطة تقع على محيط الدائرة، أي: تبعد عن المركز مسافةً مساوية لنصف القطر. | ||
| نقطة خارجيَّة | نقطة تقع خارج الدائرة، أي: تبعد عن المركز مسافةً أكبر من نصف القطر. | [ملاحظة 20] | |
| نقطتان متقابلتان | أو النقطتان المتقابلتان قطريَّاً هما نقطتا طرفي قطر ما في الدَّائرة |
إنَّ التعريفَ الرياضيَّ المُقابلَ للجدول السابق بالإمكان التعبير عنه بمبرهنة المجموعات كالآتي: إذا كانت الدائرة مركزها والنقطة المتغيِّرةُ ، فإنَّ مجموعة نقاط في المستوى تُعرَّف على أنَّها:[ِ 1][ِ 2][39] تُصنَّفُ مجموعةُ النقاطِ الداخليةِ على أنَّها مجموعة محدبة: أي أن الضلع الواصل بين أي نقطتين داخل الدائرة لا يقطعها.[ِ 2]
لتكن ولتكن من تعريف مجموعة النقاط الداخلية فإن ، ولأن على القطعة المستقيمة فهذا يعني أن إحدى الزاويتين غير منفرجة.[ملاحظة 21] بفرض - دون فقد العموميَّة - أنَّ ، بتطبيق متباينة المثلث في المثلث : إذن .
يُعرف زوج النقاط التي تمثل طرفي قطر في دائرة على أنهما نقطتان متقابلتان، وهما متماثلتان بالنسبة لمركز الدائرة. تُعرَّف مجموعة أزواج النقاط التي تحقق ذلك رياضياً:.[ِ 2]

قوة النقطة
تُعرّفُ قوةُ نقطة ما بالنسبة لدائرة ثابتة على أنها مربع المسافة بين النقطة ومركزِ الدائرة مطروحاً من مربع نصف قطر الدائرة. رياضيّاً: في قوة النقطة بالنسبة للدائرة هي المقدار:. نتيجةً لذلك، إنَّ قوةَ النُقطةِ تكونُ مقداراً سالباً عندما أي أّنها نقطةٌ داخليةٌ للدائرة، وتكون مقداراً مُنعدماً عند وقوعها نقطةً مُحيطيّةً، ومقداراً موجباً عندما تقع خارج الدائرة. في الصيغِ الرياضيةِ لمبرهنات قطع الوتر والقاطع وقاطع التماس، يظهرُ في جميعِها مقدار قوة النقطة؛ لذا فإنها تُسمّى جميعها بمبرهنات قوة النقطة. أيّ أنَّ هو مقدارٌ ثابت لكل نقطة ودائرة ثابتتين، وأنَّ أي خط مستقيم يمر بهذه النقطة فإن الصيغ الرياضية المرتبطة به تساوي .[ِ 8][50][51]
كما تُعرّفُ قوة النقطة الواقعة خارج دائرة على أنّها مُربّعُ المماس الخارج من هذه النقطة إلى الدائرة. وتُثبت هذه العلاقات باستخدام مبرهنة فيثاغورس ومبرهنة تعامد شعاع الدائرة مع المماس عند نقطة التماس: لتكن نقطة تماس المماس الخارج من إلى الدائرة . من مبرهنة التعامد: ، بتطبيق فيثاغورس في المثلث القائم: ، فإنَّ أو بشكلٍ مكافئ:.[ِ 8][ِ 3]
| الاسم | الصيغة الرياضية | النص |
|---|---|---|
| مبرهنة قِطَع الوتر | إذا تَقاطعَ وَتَرانِ في دائرةٍ فَإنَّ حَاصلَ ضَرْبِ طُولَيْ جُزأيْ الوَتَرِ الأوَّلِ يُساوي حَاصِلَ ضَرْبِ طُولَيْ جُزْأيْ الوَتَرِ الثَّانِي. | |
| مبرهنة القاطع | إذا رُسِمَ قَاطِعَانِ لدائرةٍ من نُقطَةٍ خَارِجها، فإنَّ حَاصِلَ ضَرْبِ طُولِ القاطِعِ الأوَّلِ في طُولِ الجُزْءِ الخَارِجِيِّ مِنهُ، يُساوي حَاصِلَ ضَرْبِ طُولِ القَاطِعِ الثَّانِي فِي طُولِ الجُزْءِ الخَارِجِيِّ مِنهُ. | |
| مبرهنة قاطعُ التَّماسِ | إذا رُسِمَ مَمَاسٌّ وقَاطِعٌ لدائِرَةٍ من نُقطَةٍ خَارِجها فإنَّ مُربَّعَ طُولِ المَماسِ يُساوي حَاصِلَ ضَرْبِ طُولِ القَاطِعِ في طُولِ الجُزءِ الخَارِجِيِّ مِنْه.تEعرف في الهندسة المستوية بأنها عدد حقيقي يعبر عن المسافة النسبية لنقطة معطاة في دائرة.[52] |
 |
 |
| مبرهنتا قِطَعِ الوترِ والقاطع. | مبرهنة قاطعِ التَّماسِّ. |
أزواج الدوائر
| دائرتان متباعدتان | دائرتان متماستان | دائرتان متقاطعتان | |||
|---|---|---|---|---|---|
| دائرتان لا تشتركان في أي نقطةٍ | دائران تمسان مستقيماً في نقطةٍ مشتركةٍ | أعلى عدد ممكن من التقاطعات بين دائرتين هو تقاطعان. | |||

|

|
خارجيَّاً | داخليَّاً | 
|

|
| دائرتان متماسَّتان يقع مركز كلِّ منهُما خارج مُحيط الأخرى | دائرتان متماسَّتان يقع مركز إحداهما في قرص الأخرى | ||||

|

| ||||
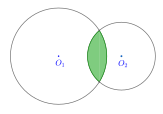
الدائرتان المتقاطعتان هما دائرتان تشتركان بنقطتين وهو أعلى عدد من النقاط الممكن اشتراكه بين دائرتين. يُعبّر عن ذلك رياضياً كالآتي: باعتبار نصف قطر الدائرة الأولى و نصف قطر الدائرة الأخرى فإن المستقيم الواصل بين المركزين يحقق المعادلة:[54]

|
 |
 |
 |
| الدائرتان المُتعامدتان: في الهندسة التعاكسية، هما دائرتان، المماسان لهما في نقطتَيْ تقاطُعِهِما يمر بمركزِ كُلٍّ منهُما. | الدائرتان المتطابقتان: دائرتان لهما نصف القطر نفسه. | الدائرتان متحدتا المركز أو في الهندسة التعاكسية: الدائرتان المتوازيتان هما دائرتان يشتركان في المركز نفسه. | الدائرتان المنطبقتان: دائرتان متحدتان مركزياً لهما الشعاع نفسه. |
الدائرتان متحدتا المركز: التي نصف قطرها و التي نصف قطرها دائرتان متحدتا المركز. تُعرف الدَّائرة على أنها مُطابقةٌ إلى دائرةٍ أُخرى إذا وفقط إذا تطابقت أنصاف أقطارهما، ويحققان: .[ِ 2]

|
|

|
|
| الحلقة: شكل شبيه بالخاتم محصور بدائرتين متحدتيّ المركز. | العدسة: تقاطع قرصين. الهلال: جزء الدائرة غير المتقاطع. | مثلث رولو: تقاطع 3 دوائر تمر كل منهم في مركز الأخرى | الأربيلوس: أنصاف دوائرَ تشترك في قاعدة ما |


تُسمَّى العدسة الناتجة عن تقاطع دائرتين متطابقتين عدسة متناظرة، عدا ذلكَ فتُسمّى عدسة جامعة أو غير متناظرة. تُقاس مساحة العدسة المتناظرة بدلالة زاوية القوس المحصورة به بالراديان ونصف قطر الدائرتين بالصيغة الآتية:[57][58]بإزالة العدسة من إحدى الدوائر المُتقاطعة يتكوَّن شكل الهلال. وبشكل أكثر عمومية، فإن تقاطع أي دائرتين يُنتج عدسةً وهلالينِ. هلال أبقراط هو هلال مُتكوِّن من تقاطع دائرتين، قُطر إحداهما هو وترٌ في الأخرى.[59][60]
الأوتار والمستقيمات

| المستقيم | التعريف | رياضياً | ملاحظة |
|---|---|---|---|
| مستقيمٌ قاطِعٌ | مستقيم يقطع الدائرة في نقطتين. | مُستقيمٌ يبعدُ عنِ المركزِ مَسافَةً أصغر من نِصْفِ قِطرِ الدَّائرةِ () | [ملاحظة 22] |
| مستقيمٌ مَاسٌّ | مستقيم يُمسّ الدَّائرة في نقطة وحيدة. | مُستقيمٌ يبعدُ عنِ المركزِ مَسافَةً مساويةً لنِصْفِ قِطرِ الدَّائرةِ () | [ملاحظة 23] |
| مستقيمٌ مَارٌّ | مستقيم لا يمس ولا يقطع الدائرة في أي نقطة. | مُستقيمٌ يبعدُ عنِ المركزِ مَسافَةً أكبر من نِصْفِ قِطرِ الدَّائرةِ () | [ملاحظة 22] |
| مستقيمٌ مُنَصِّفٌ | مستقيم يمر بمركز الدائرة. | مستقيم يمر بنقطة المركز، أو بُعدُه عن المركز معدومٌ. () | [ملاحظة 22] |

|

|

|
| المستقيم | التَّعريف | الترميز |
|---|---|---|
| خطُّ مركزين | مستقيم يصل بين مركزي دائرتين | |
| وتر مُشترك | وتر طرفاه هما نقطتا تقاطع دائرتين | |
| مَماسٌ مشتركٌ خارجيّ | أو مماس خارجي، مستقيم يمس كلتا الدائرتين ويقطعُ امتدادَ خَطِّ المَركزين. | |
| مماسٌ مشتركٌ داخليّ | أو مماس داخلي، مستقيم يمس كلتا الدائرتين ويقطع القطعة الواصلة بين المركزين. | |
| قطعة تماس | قطعة من مماس مشترك طرفاها نقطتا تماس الدَّائرين | |
| محور أساسي | المحل الهندسي لمجموعة النقاط في المُستوى التي لها نفس القوة بالنِّسبة لدائرتين مُتباعِدَتين. |
التناظر في الدائرة

في نظرية الزمر، الدائرة هي أكثرُ الأشكالِ تناظراً. أيُّ مُستقيمٍ مُنصِّفٍ (خطٍّ مُستقيمٍ يمرُ بمركزِ الدائرةِ) يُحَقِّقُ خاصيةَ التناظر الانعكاسي وخاصيةَ التناظر الدوراني. زُمرة تماثل الدائرة هي زمرةٌ متعامدةٌ . زمرة الاستدارات الخاصة بالدائرة تُسمى زمرة الدائرة () وتُعرّف على أنها زمرة ضربية تحتوي على جميع الأعداد المركبة التي معيارها مساوٍ لـ1.[61]
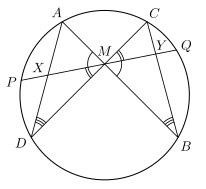
في الدائرة ذات المركز والوتر ، المثلث متطابق الضلعين. إذا كانت نقطة منتصف فإنَّ من تطابق (SSS)، وعليه فإنَّ وكذلك . أيضاً الزاويتان . إذا كانت نقطتا تقاطعِ المستقيمِ مع الدائرة، فإنَّ من تطابق (SSS) والذي يُنتج . كنتيجة، القوسان متطابقان أيضاً. بالمثل، (من تطابق SAS) و. وهذا يعني أن الدائرةَ ونقطتي مُنتصفي القوس الأكبر والقوس الأصغر جميعهم يقعون على العمود المنصف للوتر . إذن، مركز أي دائرة هو تقاطع المنصفين العموديين لأي وترين على الدائرة.[49][ِ 8]
إذا كانت تقاطع مماسات الدائرة عند ، فمن مبرهنة فيثاغورس، . مما يعني أنَّ . بعبارةٍ أخرى، قطعتا التماس المنطلقة من نقطة إلى دائرة متطابقانِ. من تطابق (SSS تطابق) فإنَّ ، إذن، الزاوية ، ومن النتيجة السابقة، فإنَّ تقع على المنصف العمودي لـ. إذا قطع مُستقيمان مُتوازيان الدائرة في فإنَّ الشكلَ الناتج هُو شبه مُنحرف متطابق الساقين. والعكس صحيحٌ أيضاً، فإن كُلَّ شبهِ مُنحرفٍ متطابق الساقين يُعدُّ رباعيَّاً دائريَّاً.[49][ِ 8]
تتلخَّصُ النتائج السابقة في ما يلي:[49][ِ 3][ِ 2]
- أي مستقيم يمر بمنتصف وتر، يتعامد عليه إذا وفقط إذا نصَّف القوسين اللذين يحصرهما الوتر. وهذا يكافئ أن يمر بمركز الدائرة.
- يتساوى وتران في الدائرة إذا وفقط إذا وقعا على مسافةٍ متساويةٍ من مركز الدائرة.
- الوتران في دائرة يتوازيان إذا وفقط إذا حصرا قوسين متساويي القياس.
- المماس عند نقطة التماس يتعامد مع نصف القطر الواصل بينها وبين المركز.
- المماسان من نقطة واحدة خارج الدائرة متطابقان.
التطابق في الدائرة
ليكن وتراً في الدائرة . بتطبيقِ متباينة المثلث: لكنَّ ، إذن بالتعويض ينتجُ . أي أنّ: «طول أي وتر داخل الدائرة لا يزيد عن طول القطر». وتحصل المساواة عند تلاشي المثلث وانتماء مركز الدائرة إلى الوتر أي كون قطراً في الدائرة.[ملاحظة 24] في الدَّائرة نفسها أو في الدَّوائر المُتطابقة، يتطابق قوسان إذا وفقط إذا تطابقت الزاويتان المركزيَّتان المتقابلتان معهما. والعكس صحيحٌ أيضاً، أي أنَّ أطوال أوتار الدائرة الواحدة أو الدوائر المتطابقة، تتساوى إذا وفقط إذا تساوت قياسات أقواسهما المتناظرة. بفرض أن الوترين لهما الطول نفسه في الدائرة ، من تساوي أشعة الدائرة الواحدة يكون: . وعلى ذلك ، وبما أن الزوايا المتناظرة لمثلثين متطابقين متطابقة ينتج المطلوب. مبرهنة: الوتر الأكبر يحصر قوساً ذا قياسٍ أكبر من قياس القوس الذي يحصره الوتر الأصغر. والعكس صحيح. كما أنَّ الوترَ الأكبرَ يبعُدُ بعداً عن مركز الدائرة أقل من بعد الوتر الأصغر.[ِ 2]
العمق وطول الوتر

عمق القوس (بالإنجليزية: Sagitta) هو قطعة مستقيمة تصل بين منتصف قوسٍ ومنتصف وتره.[62] تُستعمل حسابات عمق القوس بكثافة في العمارة. يُحسب عمق القوس ذي الزاوية في الدائرة التي نصف قطرها بالصيغة:[ملاحظة 25]
بشكلٍ مُماثل، يُقاسُ طول الوتر المحصور في قوس قياس زاويته بالصيغة .[63] أما إذا أُعطي وترٌ طوله وقوسٌ يحصر الوتر ذو عمقٍ مساوٍ لـ فباستعمال مبرهنة فيثاغورس يُقاس نصف قطر الدائرة المارَّة بالوتر وعمق القوس كالآتي:[64][65]
خط القوة

 .
.خط القوة أو المحور الأساسي (بالإنجليزية: Radical axis) لدائرتين ما، هو المحل الهندسي للنقاط في المستوى التي تتساوى قُوَّتها بالنسبة لهما.![]() وبشكل مكافئ، إذا كانت الدائرتان متباعدتان ولا تحتوي إحداهما الأخرى فبالإمكان تعريف خط القوة على أنه المحل الهندسي للنقاط في المستوى التي يكون طول المماسين المارين بها والمماسين للدائرتين متساوٍ. المحور الأساسي دائماً يتَّخذ خطّاً مستقيماً تكون نقاطه متساوية القوى بالنسبة للدائرتين؛ ولذلك فإنه يُسمَّى بخط القوة. عدا أنه في حالة اتحاد الدائرتين مركزياً يصبح خط القوة غير مُعرَّف. وفي حالة تقاطع الدائرتين، فإن خط القوة يمر بنقطتي تقاطعهما أو تماسهما. خط القوة عمودي دائماً على الخط الواصل بين مركزي الدائرتين وهو أقرب لمحيط الدائرة الأكبر. ومن خصائصه:[66][ِ 3]
وبشكل مكافئ، إذا كانت الدائرتان متباعدتان ولا تحتوي إحداهما الأخرى فبالإمكان تعريف خط القوة على أنه المحل الهندسي للنقاط في المستوى التي يكون طول المماسين المارين بها والمماسين للدائرتين متساوٍ. المحور الأساسي دائماً يتَّخذ خطّاً مستقيماً تكون نقاطه متساوية القوى بالنسبة للدائرتين؛ ولذلك فإنه يُسمَّى بخط القوة. عدا أنه في حالة اتحاد الدائرتين مركزياً يصبح خط القوة غير مُعرَّف. وفي حالة تقاطع الدائرتين، فإن خط القوة يمر بنقطتي تقاطعهما أو تماسهما. خط القوة عمودي دائماً على الخط الواصل بين مركزي الدائرتين وهو أقرب لمحيط الدائرة الأكبر. ومن خصائصه:[66][ِ 3]
- خط القوة لدائرتين عمودي على المُستقيم المار بمركزيهما ويُنصِّفُ وترَهُما المُشتركَ.
- خط القوة لدائرتين متقاطعتين يمر بنقطتي تقاطعهما.
- خط القوة لدائرتين متماسَّتين يمر بنقطة تماسّهما ويكون حينئذٍ مماسَّاً مُشتركاً لهما.
- خط القوة لدائرتين مُتماسّتين من الخارج يمر بمنتصف قطعة المماس المُشترك الآخر لهما.
- لأي ثلاث دوائر مراكزها ليست على استقامةٍ واحدةٍ، فإن محاورها الرَّئيسيَّة مثنى مثنى تتقاطع في نقطة واحدة تُسمَّى المركز الأساسي أو مركز القوة للدوائر الثلاث.
مركز القوة
لتكن دوائرَ غير متحدةٍ مركزياً مثنىً مثنىً. فإنَّ مبرهنة خط القوة تنصُّ على أنَّ الثلاثَ خطوط القوة لكل زوجِ دوائرَ إما أن تتوازى أو تلتقي في نقطة تُسمَّى: مركز قوة الدوائر. ويُقال تقنياً أيضاً عن خطوط القوى عندما تتوازى بأنّها تلتقي في نقطة في اللانهاية.[66]
وبُرهانُ ذلك: من خواصّ خط القوة لزوجِ دوائرَ، أنَّ المماسات المنطلقة من نقطة تقع عليه لدائرتين تتطابق. فإذا التقى خطّ قوة الدائرتين مع محور الأساسي الدائرتين في نقطة فإنَّ المماسات المنطلقة من لجميعِ الدوائرَ تتطابق، أي أنَّ: وأيضاً فبالتعدّي، يُصبح وبتطبيق عكسِ مبرهنة خط القوة، فإنّ النقطة تقعُ على خط القوة للدائرتين وبذلكَ يحصل تلاقي جميع خطوط القوة في النقطة . من البرهانِ السابق، تَصيرُ النقطة مركزاً لدائرةٍ تقطعُ الدوائر الثلاث. وتُعدّ هذه الدائرةُ دائرةً وحيدةً لكُلِّ 3 أزواج من الدوائر وتكون مُتعامِدةً عليهم جميعاً.[66]
العلاقات مع المضلعات
| حالات وعلاقات الكائنات الهندسية فيما بينها | |
|---|---|
| تسامُتٌ | تلاقٍ |
| توازٍ | تعامد |
| تنصيف | انطباقٌ |
| دَائريَّةٌ | تماس |

| |
| السعي نحو اللانهاية | انعدامٌ |
| مُخالَفَةٌ | اشتراك في مستوى |
لِكلّ مثلثٍ[ملاحظة 26] ثمَّةَ دائرةٌ وحيدةٌ تمرُّ برؤوسه. وتُسمَّى هذه الخاصيَّة التي تتمتع بها المُضلعات من أن تقع رؤوسها على دائرة ما «الدّائريَّة»، فيُقال عن المُضلّع أنه «دائري» إذا وُجدت دائرة تمر بجميع رؤوسه. أما النقاط التي تتمتع بهذه الخاصية فتُسمَّى نقاطاً مُشتركةً بدائرةٍ. على الرغم من ان جميع المثلثات دائرية، إلا أنّ ليست جميع المُضلَّعات الأخرى تتمتع بنفس هذه الخاصية. فعلى سبيلِ المثال، جميعُ المضلّعات المُحدَّبة تستحيل وجود دائرة تمر بجميع رؤوسها، وليست جميعُ الرباعيات لها دوائرَ مُحيطة. فجميعُ المُعيَّنات غير المربعة لا يُمكن أن تقع رؤوسها على دائرة. هناك أشكال شهيرة تُصنَّف دائماً على أنها دائرية، من ضمنها المستطيل وشبه منحرف متساوي الساقين، واللذان يُصنّف من ضمنهما المُربّع أيضاً وكذلك المُضلَّعات المُنتظِمة. للرباعيات الدائرية والمضلعات الدائرية الأخرى عموماً نظريات خاصة تنطبق عليها.[ِ 2][67]
هُناك علاقة أخرى تربط الدائرة بالمضلعات، وهي التّماسُّ. تُعرَفُ المضلعاتُ المماسيَّة على أنها مُضلّعات توجد لها دائرة تمسُّ جميعَ أضلاعها أو امتداداتها. جميع المُثلَّثات والمُضلّعات المنتظمة مُضلعات مماسية. ولها خواص ونظريات خاصة تنطبق عليها أيضاً.[67]
المُثلَّث

تُصنّف مراكز الدوائر الخاصة بالمثلث على أنها من مراكز المثلث. من أبرزها: دائرة المثلث الداخلية، دائرة المثلث المحيطة، دائرة النقاط التسع و3 دوائرَ خارجية للمثلث.[ِ 3][ِ 8] لكل مثلث يُوجد دائرة وحيدة تمس جميع أضلاعه تُسمَّى الدَّائرة الدَّاخلية أو الدَّاخلة. الدَّوائر الخارجيَّة لمثلث لكل مثلث توجد ثلاث دوائر خارجية تمس امتدادات أضلاعه. تُنشأُ الدوائر الماسة للمثلث[ملاحظة 27] بأخذ منصفات الزوايا الخارجية والداخلية للمثلث، إذ تتقاطع هذه المنصفات في مراكز الدوائر الماسة. يمرُّ خط أويلر ![]() بمركزَي الدائرتين البارزتين في المثلث: دائرة النقاط التسع ودائرته المحيطة، بالإضافة إلى نقطتي ملتقى ارتفاعات المثلث وملتقى متوسطاته. كما تربط مبرهنة فويرباخ
بمركزَي الدائرتين البارزتين في المثلث: دائرة النقاط التسع ودائرته المحيطة، بالإضافة إلى نقطتي ملتقى ارتفاعات المثلث وملتقى متوسطاته. كما تربط مبرهنة فويرباخ![]() بين أبرز دوائر المثلث: دائرة النقاط التسع ودوائره الماسة: الدائرة الداخلية والدوائر الخارجية الثلاث.[68][ِ 8]
بين أبرز دوائر المثلث: دائرة النقاط التسع ودوائره الماسة: الدائرة الداخلية والدوائر الخارجية الثلاث.[68][ِ 8]
-
يقع مركز محيطة مثلثٍ ما داخلَه إذا وفقط إذا كانت جميع زوايا المثلث حادة.
-
يقع مركز مُحيطة مثلث قائم على وتره (مبرهنة طاليس).
-
يقع مركز محيطة مثلث حاد خارجه.
تُعطى الإحداثيات الخطية الثلاثية لمركز دائرة المثلث المُحيطة بالصيغة:[24][ِ 8]يرتبطُ نصفُ قطرِ مُحيطةِ الُمثلَّثِ بعلاقةٍ هامّة تُسمّى قانون الجيوب أو قانون الجيوب المُوسَّع:[ِ 3][ِ 8]كما يُعبّرُ عنه في علاقاتٍ أخرى مُشتقّةٍ من قانون الجيب الموسّع وصيغة هيرون لمساحة المثلث:[24][ِ 8]

والصيغةُ المُثلَّثية المكافئة لما سبق تكون كالآتي:[24][ِ 8]
تربط مبرهنة أويلر في الهندسة بين شُعاعَي الدائرة المحيطة والدائرة الداخلية بالعلاقة:[69][70][ِ 8]تُقاسُ المسافةُ بين مركز محيطة المثلث ونقطة تقاطع ارتفاعاته بالصيغة:[71][72]

تنص مبرهنة كارنو على أنَّ مجموع الأبعاد المُؤشّرة من مركز محيطة المثلث إلى أضلاعه يساوي مجموع شعاعَيْ دائرتَيْ المثلث المحيطة والداخلية:[73]دائرة النقاط التسع هي دائرةٌ في المثلث تَمُرُّ بتسعِ نقاطٍ مُهمّةٍ فيه. تحديداً:[74][75][76][ِ 8]
- منتصف كل ضلع المثلث.
- مسقط كل رأس المثلث.
- منتصف كل قطعة واصلة بين رأس المثلث وملتقى ارتفاعاته.
من تعريفات دائرة النقاط التسع أنَّها صورة دائرة المثلث المحيطة بعد تحاكٍ مركزه ملتقى الارتفاعات ومعامل تصغير النصف. وكنتيجة، فإنَّ قطر دائرة النقاط التسع يساوي نصف قطر الدائرة المحيطة. وكذلكَ فإنَّ دائرة النقاط التسع تمر بمنتصف أيّ وتر يمر بنقطة ملتقى ارتفاعات المثلث. بينما بشكلٍ مُشابه، يُنصّف مركز دائرة النقاط التسع (والذي يُرمز إليه بالنقطة ) القطعة المستقيمة الواصلة بين مركز محيطته ونقطة ملتقى ارتفاعاته أي أنَّ: .[68][ِ 8]
الرباعي الدائري

الرباعي الدائري هو مُضلع رباعي تُوجَدُ دائرةٌ تمرُّ بجميعِ رؤوسِه.[ملاحظة 28] الشروط المذكورة للرباعي الدائري هي شروط مُتكافئة، أي أنَّ تَحقُّقَ أحد الشروط يُؤدي إلى تحقُّقِ بقيةِ الشروط. تُعرَف أيضاً الشروط على أنها شروطٌ كافية وضرورية أي أنَّ تحقُّقَ عكسِ الشرط المذكور يُؤدّي إلى أن يكونَ الرباعيُّ دائرياً. يُعدُّ الشكلُ الرُّباعيُّ دائريَّاً إذا وفقط إذا:[ِ 3][77]
- تقاطعت مُنصَِفاتُ أضلاعِه العموديةِ في نُقطَةٍ واحدةٍ.
- وُجِدَت زاويتان مُتقابلتان فيه مُتكاملتان.
- وُجِدَت زاويتان متساويتان رأسهما إحدى رأسي الرُّباعي على جهةٍ واحدةٍ من قاعدته. (رياضيّاً: )
- انطبقَ عليه عكسُ مبرهنة بطليموس.

- انطبقت عليه عكس مبرهنة قوة النقطة.

جميعُ المربعات، المستطيلات، أشباه المنحرف متطابقة الساقين وأضداد متوازي الأضلاع رباعيات دائرية. بينما الطائرة الورقية تُعدُّ دائريةً إذا وفقط إذا احتوت على زاويتين قائمتين. والرباعي التوافقي هو دائري يكون فيه حاصل ضرب أطوال أضلاعه المتقابلة متساوٍ.[78][ِ 8]
بحسب صيغة مساحة براهماغوبتا، تُحسَب مساحة الرباعي الدائري الذي أطوال أضلاعه: ونصف محيطه حيث بالصيغة الآتية:[ِ 8][79]
في القرن الخامس عشر الميلادي، استنتج العالم الهندي ڤاتاسِّيري پاراميشڤارا صيغة إيجاد نِصفِ قُطرِ الدَّائرةِ المُحِيطَةِ بدلالةِ أطوالِ الأضلاعِ ونصف المحيط:[79][ِ 8]
مُضلَّعاتٌ مماسيَّة

المُضلَّع المماسي هو مضلع تُوجد دائرة ما تمس جميع أضلاعه. تُسمَّى هذه الدَّائرة: الدَّائرةَ الدَّاخليَّةَ للمضلَّع. الرُّباعي المُحيط بدائرة يختص بأن كل مجموع طولي كل ضلعين متقابلين منه متساوٍ. فإذا كان الرباعي المُحيط دائرياً أيضاً سُميَّ رباعيّاً ثُنائيَّ المركزِ.و يُختص الرباعي ثنائي المركز (بالإنجليزية: Bicentric quadrilateral) على أنه رباعي مماسي ودائري ومن خواصه أنَّ مجموعَ أطوالِ أضلاعِه المتقابلةِ مُتساوٍ. بينما الرباعي ثنائي المركز الخارجي (بالإنجليزية: Ex-bicentric quadrilateral) هو رباعي مماسي خارجي ودائري في الوقت نفسه.[78][80][ِ 8]
يحتوي المضلع المحدب على دائرةٍ داخليةٍ إذا وفقط إذا التقت جميع منصفات زواياه في نقطة وحيدة. تُعرف هذه النقطة على أنها مركز دائرته الداخلية. أما إذا كانت أضلاع مضلع ذو رأس هي ومساحته ونصف محيطه فإنَّ نصف قطر دائرته الداخلية يُحسب بالصيغة:[81]
مبرهنات
بالإضافة إلى مبرهنتَيْ خطُّ القوة![]() وقوة النقطة
وقوة النقطة![]() اللتين ذُكرتا وبقية مبرهنات الزوايا الخاصة بالدائرة
اللتين ذُكرتا وبقية مبرهنات الزوايا الخاصة بالدائرة![]() ، فإنّ هناك مبرهناتٌ أخرى مُتعلقةٌ بالدائرةِ، من أبرزها وأكثرها استعمالاً:
، فإنّ هناك مبرهناتٌ أخرى مُتعلقةٌ بالدائرةِ، من أبرزها وأكثرها استعمالاً:
مبرهنة بطليموس
مبرهنة بطليموس هي مبرهنة تربط بين أضلاع الرباعي الدائري وقطريه. سميت هذه المبرهنة نسبةً لعالم الفلك والرياضيات الإغريقي بطليموس. وتنص على أنَّ مجموع جداء كُلٌّ من ضلعي رباعي متقابلين مُساوٍ لجداء قُطرَيْه إذا وفقط إذا كان الرباعيُّ دائريّاً. يُعبَّرُ عن العلاقةِ السابقة رياضياً كالآتي: . كما أنَّ عكسَ المبرهنةِ صحيحٌ أيضاً.[82][83][ِ 8]
خط أويلر
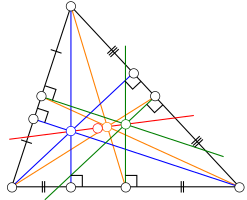
خط أويلر، نسبةً إلى ليونهارد أويلر، هو مُستقيمٌ مُعرّفٌ لكلِّ مثلثِ مختلف الأضلاع. يمرُّ بعدّة مراكز بارزة للمثلث. حيث يمر من عدة نقاط هامة محددة في المثلث. برهن أويلر في عام 1767م أن أربعة من مراكز المثلث تتسامت، وهي: ملتقى الارتفاعات ، ملتقى المتوسطات ، مركزَي الدائرتين المحيطية ودائرة النقاط التسع . تنطبق هذه النقاط عند كَوْنِ المثلث متطابقَ الأضلاعِ. يمكن رسم مستقيم أويلر بإيجاد أي نقطتين من النقاط الأربعة والوصل بينهما.[84]
خط سيمسون
خط سيمسون (بالإنجليزية: Simson line) هو مستقيمٌ يمُرّ بمساقط نقطةٍ مشتركةٍ مع مثلثٍ في دائرته المحيطة على أضلاعه. رياضياً: إذا كان مثلثاً ذو دائرةٍ محيطةٍ والنّقطةُ واقعةٌ عليها ومساقطها على مستقيمات المثلث هي على الترتيب، فإنّ النقاط هي نقاطٌ متسامتةٌ ويُسمّى خطّها خط سيمسون. كما أنَّ عكسَ المبرهنة صحيحٌ أيضاً؛ إذا تسامتت مساقطُ نقطةٍ على أضلاع مثلث، فلا بدَّ أنَّ تقع هذه النقطة على دائرة المثلث المحيطة. بالإمكان التعبير عن ذلك أيضاً بأنَّ نقطةً ينعدمُ عندها مثلث المساقط إذا وفقط إذا وقعت على دائرته المحيطة.[85][86][87]
مبرهنة باسكال

في الهندسةِ الإسقاطية، تنصُّ مُبرهنةُ باسكال (بالإنجليزية: Pascal's theorem) على أنَّ لأيّ ستِّ نقاطٍ على قطعٍ مخروطيٍّ (أي: قطع ناقص، مكافئ أو زائد) وُصِلَت بينَهم قطعٌ مستقيمةٌ بأيّ ترتيبٍ بحيث تُشكّل سداسياً، فإنَّ أزواجَ الأضلاع المتقابلة من السداسي (أو امتداداتها) تتتلاقى في نقاطٍ تتسامتُ على خطّ يُسمّى خطَّ باسكال للسداسي. أسميت المبرهنة نسبةً إلى بليز باسكال، وتصحُّ أيضاً في الهندسةِ الإقليدية إلا أن هناك حالة خاصة من أن تتوازى المستقيمات ينبغي أن تؤخذ بعينِ الاعتبار.[88]
الصيغة الرياضية لمبرهنة باسكال هي كالآتي: لأي سداسي تقع رؤوسه على قطعٍ مخروطيٍّ فإنّ ملتقياتِ أزواج المستقيمات الآتية مُتسامتة:[89][ملاحظة 29]
.
كنتيجة لمبرهنة باسكال، تنتج العلاقة الآتية بين أطوال الأضلاع:[89]
مبرهنة مونج

تنصُّ مبرهنة مونج (بالإنجليزية: Monge's theorem)، نسبةً إلى غاسبار مونج، على أنَّ لأيِّ 3 دوائر في المستوى لا تقع إحداهن داخل الأخرى تماماً، فإن ملتقيات أزواج المماسات المشتركة الخارجية تُسمّى مراكز التشابه الخارجية لأزواج الدوائر![]() لها متسامتة.[90] بالإمكان إثبات مبرهنة مونج باستعمال مبرهنة ديزارغ وكذلك بمبرهنة مينيلاوس، حيث تُحسَب النسب الداخلة في المبرهنة باستعمال بدلالة أشعة الدوائر.[90]
لها متسامتة.[90] بالإمكان إثبات مبرهنة مونج باستعمال مبرهنة ديزارغ وكذلك بمبرهنة مينيلاوس، حيث تُحسَب النسب الداخلة في المبرهنة باستعمال بدلالة أشعة الدوائر.[90]
مبرهنة فويرباخ
تنص مبرهنة فويرباخ (بالإنجليزية: Feuerbach's theorem) على أنّ دائرةَ النقاط التسع لمثلثٍ ما تمسُّ دوائرَه الخارجية والداخلية. تُسمّى نقطة تماس دائرة النقاط التسع مع الدائرة الداخلية نقطة فويرباخ بينما نقاط تماس دائرة النقاط التسع مع دوائر المثلث الخارجية فتُسمّى مُثلثَ فويرباخ. وتُعدُّ نقطة فويرباخ مركزاً للمثلث. أي أن تعريفها لا يعتمد على أطوال أضلاع المثلث أو موضعه. أسميت النقطة نسبةً إلى المهندس الرياضي الألماني كارل فويرباخ والذي نشر مبرهنته عام 1822م. أقصر بُرهانٍ لمبرهنة فويرباخ هي باستخدام مبرهنة كايزي التي نشرها جون كايزي عام 1866م،[91] وذلك بتطبيقها على المماسات لدوائر المثلث الخارجية والداخلية الأربع تمسُّ الدائرة الخامسة.[92][93]
مبرهنة ميكيل
مبرهنة ميكيل (بالإنجليزية: Miquel's theorem) هي مبرهنة تخص تقاطع 3 دوائر تمر برؤوس مثلثٍ ما.[94] ورياضياً: إذا كان مثلثاً واختيرت النقاط على أضلاعه فإنَّ الدوائر المحيطة بالمثلثات تُسمّى دوائرَ ميكيل، وهي دوائرٌ متلاقية في نقطة وحيدة تُسمّى نقطة ميكيل. ينطبقُ عكس مبرهنة ميكيل أيضاً، وتُبرهن باستخدام خصائص الرباعيات الدائرية الناتجة عن تقاطع الدوائر مع بعضها بعضاً ومع المثلث.[95][96]
مبرهنة كايزي

مبرهنة كايزي (بالإنجليزية: Casey's theorem) وتُعرَفُ أيضاً على أنها تعميمُ مبرهنة بطليموس ![]() ، هي مبرهنةٌ في الهندسة الإقليدية أسميت نسبةً إلى الرياضياتي جون كايزي.[97] تعريفها الرياضي هو كالآتي: لتكن دائرةً شعاعها . ولتكن أربعَ دوائرٍ غير متقاطعةٍ تقع داخل وتمسها على الترتيب. وليرمز إلى المماس المشترك الخارجي للدائرتين ذواتي المركزين ، فإنَّ مبرهنة كايزي تنصُّ على أنَّ:[98]
، هي مبرهنةٌ في الهندسة الإقليدية أسميت نسبةً إلى الرياضياتي جون كايزي.[97] تعريفها الرياضي هو كالآتي: لتكن دائرةً شعاعها . ولتكن أربعَ دوائرٍ غير متقاطعةٍ تقع داخل وتمسها على الترتيب. وليرمز إلى المماس المشترك الخارجي للدائرتين ذواتي المركزين ، فإنَّ مبرهنة كايزي تنصُّ على أنَّ:[98]
لاحظ أنَّ الحالةَ المُنعدمةَ لمبرهنة كايزي هي مبرهنة بطليموس. وعكسُ المبرهنةِ صحيحٌ أيضاً، أي إذا وجدت 4 دوائر تُحقق العلاقة السابقة فإنَّ هناكَ دائرةٌ تمسُّهم جميعاً.[97]
مبرهنة الفراشة
تنصُ مبرهنة الفراشة على أن الأوتار الواصلة بين طرفي وترين في دائرة يمران بمنتصف وتر ثالث يقطعان الوتر الثالث في نقطتين متناظرتين بالنسبة لمنتصفه. تُوصف هذه العلاقة رياضياً كالآتي: إذا كانت النقطة هي منتصف الوتر في دائرة، وُرسم وتران آخران يمران خلالها. فإنَّ المُستقيمان يقطعان الوتر في نقطتين متماثلتين حول ، أي أنَّ النقطة هي منتصف القطعة المستقيمة .[99][100]
التحويلات الهندسية
هُناكَ تحويلان هندسيانِ رئيسانِ بالنسبةِ للدوائر:
التحاكي
| مركز التشابه الخارجي لدائرتين | مركز التشابه الداخلي لدائرتين |

|

|

التحاكي (بالإنجليزية: Homothety) هو تحويل هندسي ينقل الخطوط المُستقيمة المتوازية إلى خطوط مُتوازية بمعامل تكبير عدد حقيقي غير صفري. للدائرتان المُتباعدتان مركزا تشابهٍ (أو تحاكٍ) اثنان: مركز التشابه الخارجي ومركز التشابه الداخلي. ولأنَّ جميعَ الدوائرِ مُتشابهةٌ، فإنَّه يُوجد مركز تشابهٍ (أو تحاكٍ) واحدٍ على الأقل لكل دائرتين. بالإمكان إيجاد مركزَيْ التحاكي لدائرة بعدد من الطرق. في الهندسة التحليلية، مركز التشابه الداخلي يُحسَبُ بالمتوسط الموزون لمركزي الدائرتين موزوناً بنصفي قطري الدائرتين. رياضياً، لتكن مركَزَيْ الدائرتين و هما نصفَيْ قُطريهما. فإنَّ مركز التشابه الداخلي يُحسَب عبر الصيغة:[101][102]
بينما يُحسب مركز التشابه الخارجي بصيغةٍ مُماثلة عدا أنَ الإشارة مُختلفة.[101]
كنتيجةٍ من خصائص التحاكي، يمر خط المركزين لدائرتين بمركزَيْ تشابههما الخارجي والداخلي. بالنسبة للدائرتين المُتماستين خارجياً، فإنّ طول قطعة التماس لهما مُساوٍ لوسط شعاعيهما التوافقي.[101] تربط مبرهنة مونج![]() بين مراكز التشابه الخاصة بثلاثٍ من الدوائر مثنىً مثنىً. وتنصُّ على أنَّ كلَّ ثلاثَةِ مراكزِ تشابهٍ لزوجٍ من الدوائر حاصل ضرب إشاراتها [ملاحظة 30]، فإنّ هذه المراكز متسامتة.
بين مراكز التشابه الخاصة بثلاثٍ من الدوائر مثنىً مثنىً. وتنصُّ على أنَّ كلَّ ثلاثَةِ مراكزِ تشابهٍ لزوجٍ من الدوائر حاصل ضرب إشاراتها [ملاحظة 30]، فإنّ هذه المراكز متسامتة.
التعاكس

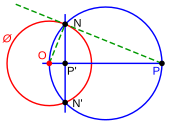
التعاكس (بالإنجليزية: Inversion) هو تحويل هندسي يعكِسُ كلَّ نُقطةٍ على المُستوى حول دائرةٍ ثابتة. يُعرّف انعكاسُ النقطة المُختلفة عن المركز حول الدائرة على أنه نُقطةٌ تقع على الشّعاع تُحقّق العلاقة: . هُناك اختلاف حول صورة المركز ، هناك من يُعرِّفُه على أن صورة هي نفسها، لكن في الغالب فإنَّه يُعرّف على أنه نقطة في اللانهاية. إنّ التعاكسَ الذي ينقلُ النقطةَ إلى صورتها أيضاً ينقل الصورة إلى الأصل ؛ وبهذا تكون دالة التحويل الهندسي الخاصة بالتعاكس دالةً ارتداديَّة، أي بعبارةٍ أخرى: الأصل يؤدي إلى الصورة والصورة تؤدي إلى الأصل.[55][103][104]
-
انعكاس دائرة مارة بمركز الدائرة أخرى حول الأخيرة، يُنتج خطاً مُستقيماً.
-
انعكاس الدائرة الخضراء هو الدائرة الزرقاء بالنسبة للدائرة الحمراء.
-
التعاكس لا ينقل مراكز الدوائر إلى بعضها بعضاً.
ينقل التعاكس كُل نقطة داخل الدائرة إلى صورةٍ نظيرةٍ لها خارجها، وكل نقطة تقع على محيط الدائرة فإنَّها تبقى كما هي. يُعبِّر هذا التحويل الهندسي عن اختزالٍ للصورة المستوى اللا نهائي الواقعة عليه الدائرة، بمعنى أنه كلما قربت النقطة من مركز الدائرة كُلمَّا كانت صورتها أبعد عن الدائرة، وكلَّما كانت النقطة بعيدة من مركز الدائرة فإن صورتها تُصبح أقرب لمركز الدائرة.[55][103]
الهندسة التحليلية
دائرة الوحدة والدوال المثلثية

يمكنُ تعريفِ الدوالِ المثلثيةِ: الجيب وجيب التمام والظل ومقلوباتها، بقيمِ إحداثياتِ النقاطِ على المستوى الإقليدي المرتبطةِ بدائرة الوحدة.[ملاحظة 31] دائرة الوحدة هي دائرة نصف قطرها وحدةٌ واحدةٌ ومركزها نقطة الأصل. رغم أن تعريفات المثلثِ قائمِ الزاوية للدول المثلثية تسمحُ بتعريفِها للزوايا بينَ 0 و راديان فقط، إلا أنَّ تعريفاتِ دائرةِ الوِحدةِ تُعمّمُ ذلك وتمدد مجال الدوال المثلثية لتسمحَ بجميع الأعداد الحقيقية الموجبةِ والسالبةِ.[105][106]
| جزء من سلسلة مقالات حول |
| حساب المثلثات |
|---|
 |
| بوابة رياضيات |
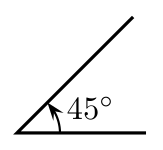
تُعطى تعريفات الدوال المثلثية من تقاطع مستقيمات مرتبطة بزاوية واقعةٍ على نقطة الأصل. إذا قطعَ الشعاعُ المنطلق من نقطة الأصل بزاويةَ
[ملاحظة 32] دائرةَ الوحدةِ في النقطة
فإنّ الدالةُ
تُعرّف على أنها الإحداثي
والدالة
هي الإحداثي
لنقطة التقاطع، وبمعنى آخر فإنَّ:
. وبرسم مماس من النقطة
يقطع محورَي السينات والصادات في النقطتين
على الترتيب، فإنَّ
.

يتطابقُ هذا التعريفُ مع تعريفِ المثلث قائم الزاوية في الفترة باعتبار أنَّ نصفَ قطرِ دائرة الوحدة هو وترٌ للمثلث القائم. ولأنّ كل نقطة على دائرة الوحدة تُحقّق أنَّ من مبرهنة فيثاغورس في المثلث القائم . فإنَّ تعريف الدوال المثلثية على أنها الإحداثيات يُنتِجُ متطابقة فيثاغورس: .[107][108] وأخيراً فإنَّ المسافات تُعرّفُ على أنّها الدوال المثلثية: على الترتيب. بشكلٍ مُشابهٍ للاستنتاج السابق، يمكن تطبيق مبرهنة فيثاغورس في بقية المثلثات القائمة للوصول إلى متطابقات فيثاغورس الخاصة ببقية المتطابقات المثلثية. ومن تشابه هذه المثلثات القائمة السابقة، تُعطى العلاقات التي تربط بين جميع الدوال المثلثية كالآتي:[109]
بما أنَّ دوراناً بزاوية لا يُغير موضعَ الشكلِ ولا حجمَهُ، فإن النقاط ستبقى نفسها بالنسبة لزاويتين فرقَهُما مضاعف صحيح لـ . وعلى ذلكَ، فإنَّ المساواةَ و صالحةٌ لأي زاوية ولأي عدد صحيح . تنطبق الخاصية ذاتها على الدوال المثلثية الأربع الأخرى.
الإحداثيات الديكارتية

في النظام الإحداثي الديكارتي، إذا كانت النقطة مركزاً لدائرةٍ نصف قطرها ، والنُّقطةُ مُتغيّرةً على مُحيطِ الدائرةِ، فإنَّ من تعريف الدائرة الذي ينص على أن البُعد بين النقطتين هو بُعدٌ ثابت مُساوٍ إلى ، فإنَّ مُعادلة تمثيل الدائرة في النظام الإحداثي الديكارتي هي الآتي:[ِ 1]
تنبثقُ هذه المعادلةُ أيضاً من مبرهنة فيثاغورس عند تطبيقها بإنشاء ضلعي القائمة على الوتر . عندئذٍ، تُصبحُ المسافتان و طُولَينِ للضلعين الآخرين في المثلث قائم الزاوية. هناك ثلاثةُ مواضعٍ للدائرةِ بالنّسبةِ للمحاورِ الإحداثيَّةِ: دائرةُ المركزِ ودائرة مماسة للمحور الأفقي ودائرة مماسة للمحور الرأسي. تُعتبرُ مُعادلة كلٌّ منها عن حالة خاصّة من مُعادلة تمثيل الدائرة في الإحداثيات الديكارتية الأصلية.
كحالة خاصّة، تُحسب معادلة دائرة المركز، وهي الدائرة التي مركزها نقطة تقاطع المحورين، عند انطباق مركز الدائرة على نقطة الأصل تُصبح المُعادلة بتعويض قيم : كالآتي[ِ 1]وبالإمكانِ كتابةُ هذهِ المعادلةِ على شكل معادلة وسيطية[ملاحظة 33] (بالإنجليزية: Parametric equation) باستعمال الدوال المثلثية: جيب وجيب تمام على الشكل الآتي:حيث أن هو وَسِيطٌ (بالإنجليزية: Parameter) تتغيرُ قيمتُه بين العددين و . هندسيَّاً، يُمثّل هذا الوسيطُ الزاويةَ التي يُكَوِّنُها الشَّعاعُ المَارُّ بالنقطتين و مع المحور الأفقي. المعادلة الوسيطية التالية تمثل أيضاً دائرة:
إذا كانت الدائرة تمس المحور الأفقي فتُسمّى دائرة مماسة للمحور الأفقي وتُصبح المُعادلة على الصورة: . وبصورةٍ مماثلةٍ، إذا كانت الدائرة مماسةً للمحور الرأسي فتُصبح المُعادلة على الصورة: .[ِ 1]
كما أنه بالإمكان أيضاً إيجاد مُعادلة الدائرة بمعلوميَّة إحداثيات طرفي قطر فيها. إذا كان قطراً في الدائرة، وكانت إحداثيَّات النقطتين هي بحيث أنهما نقطتان معلومتان عليها. تُؤخذ نقطة ثالثة على مُحيط الدائرة وبما أن قُطر في الدائرة، فإن وعليه فإن ، ليكن ميل المستقيمين هما على الترتيب، حيث:[ِ 1]
ولِكَوْن فإن وعليه تكون مُعادلة الدائرة بمعلومية طرفي قطر فيها تُصبح على الصورة:[ِ 1]إذا كانت نقطةً على دائرةٍ نصف قطرها على المستوى الإحداثيّ، فإنَّ المماسَ المنطلقَ منها تُكتَب مُعادلَتُه على الشكل:
صيغة الثلاث نقاط
بالإمكان تحديد مُعادلة الدائرة من أي ثلاثِ نقاطٍ ليست على استقامةٍ واحدةٍ: عبر المعادلة الآتية:
يُعبَّر عن المُعادلة أحياناً بالمصفوفة الصفرية الآتية أيضاً:[31]
وبالإمكان كتابتها أيضاً على صورة المعادلة التربيعية:[31]
حيثُ أنَّ
وَ:
وعلى ذلك، تُصبح إحداثيات مركز الدائرة: ونصف قطرها:[31]
الإحداثيات القطبية
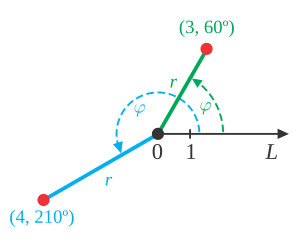
في النظام الإحداثي القطبي، المعادلة القطبية للدائرة التي نصف قطرها ومركزها عن النقطة يُمكن الحصول عليها باستخدام قانون جيب تمام الزاوية للمثلث ، حيث أنَّ النقطةَ تُعبّرُ عن أيِّ نقطةٍ على الدائرةِ وذلك على الصورة:[ِ 1]
حيث أنّ هي الإحداثية القطبية لنقطةٍ ما من الدائرة و هي الإحداثية القطبية لمركزِ الدائرةِ. حالة خاصّة من ذلك عند كون مركز الدائرة عند النقطة فإن وَ وعندئذٍ تأخذُ معادلة الدائرة في الصورة القطبية الصورة: .[ِ 1] وعند موقوع مركز الدائرة على النقطة تأخذ المعادلة الصورة: .[ِ 1]
المستوى العَقَدي

في المستوى العقدي، الدائرة ذات المركز ونصف قطر تُمَثَّلُ بالمعادلةِ . وقد تُكتب أيضاً على الصورة الوسيطية الآتية: . تُستخدم جذور الوحدة أو أعداد دي موافر أو الجذور النونية للعدد 1 من ضمن استعمالات الأعداد المركبة لإيجاد قيم دوال مثلثية وحل المسائل المتعلقة بالدائرة في الهندسة التحليلية. جذر الوحدة النوني هو عدد عقدي يقع على دائرة الوحدة، وعند رفعه للقوة ينتج واحداً.[110][111][112] تستعمل جذور الوحدة في عدة مجالات ولها أهمية كبيرة في نظرية الأعداد وحروف الزمر ونظرية الحقول وتحويل فوريي المنقطع.
التفاضل والتكامل
في الدائرة ذات القطر والشعاع ، يكون مُحيطها :[31]

بالإمكان الوصول إلى هذه النتيجة باستعمال صيغة طول القوس بالإحداثيات القطبية في التفاضل والتكامل:[31]
استعمل أرخميدس طريقةَ استنفادٍ لحساب مساحة الدائرة. قطَّع فيها الدائرةَ إلى أربعةِ قطاعاتٍ مُتساوية، ثمَّ أعاد ترتيبها وأعاد تقطيها إلى قطاعاتٍ مُتساويةٍ مُجدداً، واستمرَّ في ذلك إلى أن وصل إلى شكلٍ مُشابهٍ لمتوازي الأضلاع:[31]
| خطوة1 | خطوة2 | خطوة3 |
|---|---|---|
 |
 |
 |
| النتيجة النهائية (قبل وبعد) | ||

| ||
بُنيَت طريقةُ الاستنفادِ بناءً على افتراض أن الدائرة قُسمَّت إلى قطاعات مُتساوية، وأن الشكل الناتج الأخير سيكون قريباً جداً من متوازي الأضلاع. وعلى ذلكَ فتكونُ مساحة الدائرةِ مُساويةً لمساحةِ مُتوازي الأضلاع، والتي يُمكنُ حسابها بقانون المساحة الخاص بمتوازي الأضلاع: وهو جداء القاعدة في الارتفاع. قاعدة متوازي الأضلاع ستكون نصف المُحيط () بينما ارتفاعه هو . وعلى ذلك تُصبح المساحة الكلية . حل طريقة الاستنفاد بالإمكان إعادة صياغته لجعله أكثرَ رسميةٍ في البراهين الرياضية عبر صيغة التكامل الآتية:[31]
في الأبعاد الأخرى

الكرة
الكرة أو الفلكة هي سطح هندسي ثنائي تام التناظر، ينتج عن دوران دائرة حول أحد أقطارها.[113][114][115] تختص الدائرة في تعريفها أن تكون النقاط التي تبعد البعد نفسه عن المركز على أن تكون في المستوى نفسه أيضاً، وبهذا فإن النظير الثلاثي الأبعاد للدائرة هو الكرة، حيث أنها مجموعة النقاط التي تبعد البعد نفسه عن نقطة ثابتة في الفضاء. يتكون المقطع الجانبي للكرة من دوائر.
إذا قطع المستوى الكرةَ ، فانَّ المقطع الناتج سيكون دائرةً تُسمى دائرة المقطع. تكون دائرة المقطع أكبر ما یمكن عند مرور المستوى القاطع بمركز الكرة. وفي هذه الحالة، یكونُ نصف قطرِ الدائرة مساویاً لنصف قطر الكرة وتُسمَّى دائرة الكرة الكبرى. عدا ذلك، تسمى دائرة المقطع دائرة صغرى، لأن نصف قطرها أصغر من نصف قطر الكرة ومركزها یختلف عن مركز الكرة.[ِ 5]
الأُسطوانة
هي مجسم ينتج عن دوران المستطيل حول أحد أضلاعه دورة كاملة فتكون قاعدة الاسطوانة دائرة. وبالإمكان تعريفه أيضاً على أنه مجسم يتشكل سطحه من جميع النقاط التي تبعد مسافة معينة عن قطعة مستقيمة معطاة.[116][117][118]
الكرة الفائقة
في الهندسة الرياضية متعددة الأبعاد، الهايبرسفير أو الكرة الفائقة (بالإنجليزية: Hypersphere) هي مجموعة نقاط تبعد مسافةً ثابتةً عن نقطة مُعطاة تُسمى المركز. تُعد الهايبرسفير متعددة الشعب. ومع زيادة نصف قطرها، يزداد انحناؤها. المستويات الفائقة والكرات الفائقة هي مثال على السطوح الفائقة.[119]
إنشاءات المسطرة والفرجار


الفرجار من أكثر الأدوات شيوعاً التي تُستخدم لِرسمِ دوائرَ أو أقواسٍ دائريةٍ. والفرجار هو أداة هندسية تقنية بالإمكانِ استعمالُها أيضاً لقياس المسافات على الخرائط والمخططات المعمارية. غالباً ما يُصنع الفرجار من بلاستيك أو معدن، ويتَكوَّنُ من طرفين: أحدُهما رأسُ إبرةٍ مُدبّبةٍ والآخرُ قلم رصاصٍ أو حِبْرٍ. إلا أنه في الفترة الحالية، بعد تطور تقنيات التصوير والتصميم الحاسوبي، اختُزِلَ استِعمالُ الفرجار والمرسام كاستعمالٍ دارجٍ المدارس والجامعات لتعليم التصميم والهندسة الرياضية. تُرسَم الدائرة بتثبيت رأس الفرجار المدبب (أو الإبرة) على الورقة ووضع رأس القلم على الورقة وتدويره حول القطعة المثبتة. كما يُتَحكَّمُ بقياسٍ نصفِ قطرِ الدائرةِ عن طريق تعديل قياس الفتحة بين القطعتين: الرأس المدبب والقلم، باستخدام المفصل العلوي للفرجار.[120]
الإنشاء بمسطرة وفرجار هو إنشاء أضلاع، زوايا، وأشكال هندسية أخرى عبر استعمال المسطرة والفرجار فقط. وفي الهندسةِ الإقليدية، هاتان الأداتان هُما الوحيدتان المسموح باستخدامهما. وهو ما جعلها تُسمَّى «هندسة المسطرة والفرجار».[10][11] تربيع الدائرة، تثليث الزاوية ومضاعفة المُكعَّب كانت من أبرز المسائل الرياضية والمواضيع التي حاول فيها الرياضيون على مر التاريخ. إلى أن أثبت بيير وانتزل وفيردينوند فون ليندمان استحالة تِلكُمُ المسائل.[12]
القائمة الآتية تستعرض أبرز وأهم الإنشاءات الهندسية بالمسطرة والفرجار التي تدخل فيها الدائرة بوصفها عنصراً أساسيّاً:
- إنشاء عمود منصف لقطعةٍ مُستقيمةٍ: بافتراض أنَّ قطعة مستقيمة، ارسم الدائرتين وافترض أنهما يتقاطعان في . إنَّ هُو المنصف العمودي للقطعة المستقيمة .[ِ 5]
- إنشاء مُنصِّف لزاوية: يُنشئ منصف الزاوية كالآتي:[ِ 5]
- أنشئ الدائرة وافترض أنها تقطع شعاعا الزاوية في على الترتيب.
- ارسم الدائرتين بأيِّ نصفِ قُطرٍ ، وافترض أن إحدى نقطتي تقاطعهما هي .
- إن منصفَ الزاويةِ هو .
- لإنشاء المنصف الخارجي للزاوية، طبق الخطوات السابقة لكن مع أخذ الشعاعين: .
| إنشاء عمود منصف | إنشاء منصف زاوية | إنشاء سداسي منتظم | إنشاء مربع |
|---|---|---|---|
 |
 |
 |
 |
- إنشاء مركز مُحيطة المثلث: لتكن ، ، ثلاث نقاط ليست على استقامة واحدة. عندئذ، يكون المُنصّفان العموديّان للقطعتين وَ غير متوازيين لانعدام تَسامُتِ النقاط؛ ولذا لتكن نقطة تقاطعهما هي ، وبما أن فإن الدائرة التي تمر بالنقاط الثلاث يكون مركزها . بالإمكان تعميم هذه الطريقة لأي مُضلّع دائري، وذلك بأخذ ضلعين منه وإنشاء العمودين المنصفين له.[ِ 2][ِ 5]

إنشاءات المسطرة والفرجار هي التي ميّزت الهندسةَ الإقليدية. ولهذا كانت تُسمّى: «هندسة المسطرة والفرجار». - إنشاء مماس من نقطة خارج الدائرة: إذا كانت دائرةً، و نُقطةً خارجَها، فإنّ إنشاء مماس من النقطة إلى الدائرة يكون كالآتي:[ِ 5]
- صِلْ ولتكن نقطة تقاطعه مع الدائرة.
- خُذ نقطة منتصف ولتكن .
- ارسم الدائرة التي قطرها أو بترميز الدائرة: .
- تقاطع الدائرة مع الدائرة الأصلية هما نقطتا تماس النقطة مع الدائرة .
- إنشاء المماس المشترك الداخلي لدائرتين: لتكن دائرتين معلومتين مركزاهما على الترتيب. إنشاء المماس المشترك لهما من الداخل، يكون كالآتي:[ِ 5]
- صِل وارسم الدائرة ذات القطر ولتكن .
- ارسم الدائرتين وافرض أن نقطة تقاطعهما مع أحد نصفي الدائرة هما على الترتيب.
- صل وليقطعا الدائرتين في على الترتيب.
- كرِّر العملية مع نصف الدائرة الآخر ولتكن نقاط التقاطع هي .
- المستقيمان هما مماسان مشتركان داخليان للدائرتين الأصليتين .
إنشاءات مستحيلة
تربيع الدائرة
تربيع دائرة هي معضلةٌ وضعَها علماء الهندسة القدامى. تتمثل في إنشاء مربع مساحته تساوي مساحة دائرة معينة باستعمال عدد منته من الخطوات فقط بواسطة الفرجار والمسطرة. في عام 1882، أُثبت أن هذه المهمة مستحيلة، نتيجة لمبرهنة ليندمان-فايرشتراس التي تُبرهن على أن عدد متسام بدلا من أن يكون مجرد عدد جبري غير كسري (عدد جبري هو عدد يكون جذرا لمتعددة حدود عواملها كلها أعداد كسرية).[121]
مضاعفة المكعب
عُرفت مسألة مضاعفة المكعب في العديد من الأجناس كالمصريين، الإغريق، والهنود.[122][123] تتمثل المسألة في تحويل أي مُكعّبٍ مُعطى إلى مُكعّب ذي ضعف الحجم. رياضياً، من المكعب ذي طولِ الضلع والحجم ، المطلوب إنشاء مكعب جديد بحجم . أي أنَّ طول ضلع المكعب الجديد . أثبت استحالة عمل ذلك بإنشاءات الفرجار والمسطرة بعد إثبات استحالة وجود ضلع طوله بالمسطرة والفرجار.[124][125]
تثليث الزاوية
مسألة تثليث الزاوية تبحث حول إيجاد إنشاء بالمسطرة والفرجار برسم 3 مستقيمات تقسم الزاوية إلى 3 زوايا مُتساوية القياس. ثبت استحالة إيجاد حل باستعمال المسطرة والفرجار على صورتها العامة لأي زاوية، لكن هناك زوايا خاصة مثل 90 بالإمكان تثليثها عبر إنشاءات المسطرة والفرجار.[126][127][128]
التاريخ

عُرفت الدّائرة قبل بداية تسجيل التاريخ. ولوحظت الدّوائر في الطبيعيّة، كالقمر، الشمس والنّباتات ذات الأزهار الدّائرية. كانت الدائرة الأساس للعجلة، والتي ارتبطت لاحقاً بابتكارات أخرى كالتروس التي مكّنت من تطور الآلات الحديثة. في الرياضيات، ساعدت دراسة الدائرة في تطوير علوم الهندسة، الفلك، التفاضل والتكامل. بينما ارتبطت العلوم المُبكّرة كالهندسة، التنجيم، والفلك بالأديان عند معظم علماء القرون الوسطى، والعديد منهم اعتقد بأن الدائرة - جوهريّاً - تحمل شيئاً «مُقدّساً» أو «كاملاً مثاليّاً».[129][130] تُلخًّصُ النقاطُ الآتية أبرز الأحداث التّاريخية الهامّة في تاريخ الدائرة:
- في عام 1700 قبل الميلاد، أعطت ورقة قديمة تعود إلى ذلك الزمان طريقة تمكن من إيجاد مساحة الدائرة. تعطي هاته الطريقة قيمة مقربة ل π وهي 256 / 81 (أي 3.16049...).[131]
- في عام 300 قبل الميلاد، تحدث الجزء الثالث من كتاب أصول أقليدس عن خصائص الدوائرَ.
- في الرسالة السابعة لأفلاطون، وُجِدَ تعريفٌ وشرحٌ للدائرةِ.
- في عام 1880، أثبت فيردينوند فون ليندمان أن عدد متسام، ليحل وبشكل نهائي المعضلة المطروحة منذ آلاف السنين والمتمثلة في تربيع الدائرة.[132]
المصريون القدماء
إضافةً للنّقطة والخط المستقيم، عُرفت الدائرة على أنها من أقدم العناصر الهندسية من قبل الأغريق.[133] ففي الألفية الثانية قبل الميلاد، كانت الهندسة من المجالات التي عمل عليها المصريون القدماء، وقدّروا مساحة الدائرة، عن طريق تربيع ثمانية أتساع طول قطرها، فحسبوا المساحة كالآتي:
نسبة الخطأ التي وُجدت في حساباتهم كانت بزيادة 0.6%. ووُجد هذا التّقدير في بردية ريند الرّياضيّة، والّذي جاء بعد تقريب مساحة الدائرة إلى ثُماني غير منتظم.[133]
البابليون
استعمل البابليّون (1,900 حتى 1,600 ق.م) طريقةً مُغايرة لحساب مساحة الدّائرة. خلافاً لما فعله المصريّون، قدّر البابليَّون مُحيط الدّائرة بثلاثة أضعاف قطر الدّائرة.[ملاحظة 34] بينما قُدِّرت مساحة الدّائرة بإنها واحد من اثني عشر من مربع طول المحيط. هي:[133]
بنسبة خطأ نقص حوالي 4.5%. ارتبطت أعمال البابليين بأضلاع الدائرة أيضاً. وكانوا قادرين على إيجاد طول الوتر أو عُمقه. وبهذه الطّريقة هيَّأوا الأساس لهندسة الأوتار التي طوّرها بعدئذ هيبارخوس. ووضع بطليموس كلوديوس أساساتها في كتابه الفلكي «المجسطي».[133]
الإغريق
يُعتبر عهد الإغريق أحد الفترات الزمنية المؤثرة في توثيق الأعمال الهندسية التي من بينها الدائرة. في هذه الفترة انتشرت العديد من المؤلفات الهامة، ونُسبت العديد من النظريات لفلاسفة ورياضيي الإغريق.
طالس
يُعتبر طالس (546-624 ق.م.) أحد الفلاسفة والرياضيين المُؤثرين في فترته. إذ نقل العلوم الهندسية من مصر إلى الإغريق. وتنص المبرهنة المنسوبة إليه على أن الزوايا المحيطية لنصف الدائرة قائمة.[133]
أول تعريف وُضِعَ للدائرة يرجع إلى الفيلسوف الإغريقي أفلاطون (428/427-348/347 ق.م.) الّذي صاغها في حواره بارمنيدس:[134]
إقليدس
لم يُعرف عن الرياضياتي الإغريقي أقليدس الإسكندرية (300 ق.م.) سوى القليل. إلا أن أغلب عمله في مجال الهندسة كان له تأثيراً حتى الوقت الحاضر. إذ لا تزالُ تُنسبُ إليه بعض المفاهيم والأفكار في الرّياضيات. كالفضاء الإقليدي، الهندسة الإقليدية والقياسات الإقليدية. استخلص إقليدس مقترحاتٍ لمسلّمات رياضية، نشرها في كتابه العناصر. كما أنه وثّق أعمال الرياضيين الذين سبقوه في هذا المجال وأدرج البراهين الرياضية لنظرياتهم، يُعرِّف إقليدس الدائرة في كتابه العناصر قائلاً:[56][133]
كان كتاب العناصر لإقليدس أحد أهم أعماله ومن الكتب الرائدة في مجال الهندسة. يتكون الكتاب من 13 فصلاً جمع فيها مقالاتٍ مُلخّصة. نظّم من خلالها وعلوم الحساب والهندسة وأفكارها وقتئذ. في الفصل الثالث من الكتاب جمع إقليدس جميع المفاهيم المُتعلّقة بالدّائرة ونظّمها فيه.
أرخميدس
أثبت أرخميدس في دراساته «كرسيمس» أن مساحة الدائرة مُساوية لنصف المحيط مضروباً في نصف القطر.[135] وبهذا المفهوم فقد طرح مسألة تربيع الدائرة: «كيف تُنشئ المحيط من نصف قطر مُعطىً». وفي ورقته قياس الدّائرة حصر أرخميدس قيمة برسم مُضلّعات مُنتظمة تمس الدائرة من الخارج تارةً ومن الدّاخل تارةً أخرى وإيجادها بنسبة المُحيط إلى القطر: . ومن المتباينة يُستخدم التّقدير الشّائع، والّذي لا زال يُستعمل حتى اليوم بأن . ومن العلاقتين يُمكن استنتاج أن مساحة الدائرة إلى مربع قطرها مُساوٍ تقريباً إلى . وكان أقليدس على علم بأن مساحة الدائرة تتناسب مع مربع قطرها.[ِ 4][134] وبذلك قدَّم أرخميدس تقديراً جيّداً لهذا الثّابت النسبي.
في عمل آخر لأرخميدس «على اللوالب»[135] وصف أرخميدس إنشاءً نُسبَ اسمه إليه لاحقاً بـ«لولب أرخميدس». بهذا الإنشاء استطاع أرخميدس تحويل محيط دائرة ما إلى خط مستقيم. وبهذه الطّريقة، فإنه يستطيع تحديد مساحة الدائرة بدقة. رغم استحالة إنشاء اللولب باستعمال المسطرة والفرجار فقط.[136]
أبولونيوس
فصّل أبولونيوس البرغاوي (262-190ق.م) في قطاعه المخروطي «كونيكي» أن الإهليلج والدّائرة ما هما إلا جزئي قمع مخروطي قائم، والتّي لا زالت حتّى تُتدارس على هذا الأساس في الهندسة الجبرية. عمل على مراجعة أعمال سابقيه في هذا المجال إقليدس وأرسطيوس (حوالي سنة 330 ق.م.) وكثّف الأطروحات والدّراسات حول القطوع المخروطية.[133]
قدَّم أبولونيوس مسألةً عُرِفت لاحقاً بمسألة أبولونيوس طرح من خلالها تساؤلاً حول كيفية إنشاء دائرة تمسّ ثلاث دوائرَ باستعمال الأدوات الإقليديّة: الفرجار والمسطرة فقط. مقارنةً بالعناصر الإقليديّة، لوحِظت أعمال أبولونيوس أكثر في العالم الإسلامي. في أوروبا الغربيّة، أصبحت كتبه أكثر أهمية خلال القرن السابع عشر الميلادي، عندما لاحظ يوهانز كيبلر أن الإهليلج هو المسار الحقيقي التي تتخذه الكواكب حول الشمس.[133]
العصور الوسطى

أثناء حكم المأمون في خراسان (القرن الثالث للهجرة)، ترجم بنو موسى كتاب المخاريط لأبولونيوس من اليونانية إلى العربية. كان بحوزة بني موسى نسخة غير مكتملة من الكتب، لذا فإن القطوع المخروطية لم تنقل كاملةً وقد واجهوا صعوبةً في ترجمة العبارات. بعدئذٍ بفترةٍ، قدّم الحسن ابن موسى نظرية القطوع المخروطية التي وصف فيها بدايات وأساسيات للقطوع المخروطية. مهّد فيها مقدمةً لفهمها. بعد وفاته، أكمل أخوه أحمد الذي كان يعيش في المشرق نسخة مكتملةً من أعماله. سلم أحمد وأخوه محمد النسخة المترجمة من أول 4 فصول من كتاب المخاريط إلى هلال حمصي، ومن الفصل الخامس حتى السابع إلى ثابت بن قرة. النسخة الوحيدة التي تبقت من الترجمة هي التي كانت بحوزة بني موسى واحتوت على الفصول الخامسة والسادسة والسابعة.[137]
قدّم بنو موسى حلاً باستخدام القطوع المخروطية لمسألة تثليث الزاوية. كما قدّم أبو جعفر الخازن وأبو سهل القوهي والسجزي وأبو الريحان البيروني ثلاثَ مسائلَ مُبرهنين على أنه بحل هذه المسائل، ستحل مسألة تثليث الزاوية تباعاً. بطلبٍ من عضد الدولة بن بويه، كتب عبد الرحمن بن عمر الصوفي كتاباً بعنوان:[138] «رسالة فی عمل المتساویة الاضلاع کلها بفتحة واحدة». والذي وضّح فيه طريقةَ رسمِ مضلع منتظم باستعمال المسطرة والفرجار فقط. وفي كتابه: «فیما یحتاج إلیه الصانع من الأعمال الهندسية» أو اختصاراً كتاب «الأعمال الهندسية» بحث أبو الوفاء البوزجاني، استكمالاً على أعمال عبد الرحمن الصوفي، في رسم الأشكال الهندسية بالفرجار والمسطرة. حَسَبَ غياثُ الدين الكاشي نسبةَ محيطِ الدائرة إلى قطرها أو بدقةٍ عالية، وذلك باستعمال حصر مضلعات داخل الدائرة وخارجها. كما كتب في كتابه: «مفتاح الحساب»، رسالةً بعنوان: «رسالة الوتر والجيب»، التي فُقدِت. كما قدّم محاولةً لحل مسألة تثليث الزاوية عن طريق حل المعادلات التكعيبية.[139][140]
في الثقافة والفن
أخذت الدائرةُ الأساسَ في بناء العديد من التكوینات الفنیة وارتبطت بالعديد من المفاهيم فيها. إلا أنه مع ذلك، كان للنظرة المجتمعية والعالمية تجاه الدائرةِ تأثيراً على إدراك ونظرة الفنان لها وجعله منحازاً أكثر تجاه مفهوم معين. فثمّة من يرى أنّ شكل الدائرة المُحيط يُمثّل الوِحدَة والإيحاء بالديموقراطية، ولهذا يُوجد في مجالس الشورى والبرلمانات. بينما ترى بعض المعتقدات الروحانية على أنَّ الدائرة ترمز إلى الاستمراریة واللانهائیة والسرمدیة والتي هي طبيعة هذا العالم. في تقاليدٍ دينيةٍ أخرى، الدائرة تُمثل الأجسام السماوية والأرواح الملائكية وترمز إلى العديد من المفاهيم المُقدّسة، منها الاتحاد، الاكتمال والكون، الألوهية والاتزان، الثبات والمثالية، من بين عديد من المفاهيم. وفي الفن، تُؤوّلُ الدائرة للقدر والمصير، أو الموروث التقليدي للتشاؤم والتفاؤل على حدّ تعبير بعض الفنانيين. كما أن هناك من يربطها بالمفهوم القابع في شعار اليين واليانغ، والذي يربط بين المفاهيم المتضادة: كالخير والشر، الفناء والخلق، الموت والولادة، الفوضى والتناغم، الجمود والحركة. هذا الخليط من المفاهيم أدى إلى انتقالها بين الثقافات، فوُجدت على سبيل المثال في البوصلة، الهالة، الترميز للعين والبصيرة، وقوس القزح والدارما، ونوافذ بعض المعابد والمباني الدينية، والأوربوروس.[9][ِ 9]
في فنون الحضارات القديمة، حضرت الدائرة، للدلالة على الشمس أو القمر، مثل المنحوتات الجدارية الفرعونية، حيث يعلو الرأس قرص مستدير يرمز إلى الشمس. كما ظهرت الكرة السماوية والكرة الأرضية في عدد كبير من اللوحات الأوروبية ما بين عصر النهضة والقرن التاسع عشر. وفي معظم الأحيان للدلالة على المكانة العلمية للشخص المرسوم، أو للإشارة إلى عمله كبحار أو كجغرافي. في عام 1913م، رسم فاسيلي كاندينسكي لوحته «دوائرُ ضمن مربعات»، ليؤسس بها تيار التجريد الهندسي. وحظيت الكرة بدفع كبير في الفن البصري على يد الفنان فيكتور فازاريلي الذي رسم عشرات اللوحات المؤلفة من مربعات هندسية تماماً، تبدأ أضلاعها بالتقوس كلما اقتربت من وسط اللوحة، لتشكِّل ما يبدو كرة أو نصف كرة، ناتئة من اللوحة التي هي في الواقع مسطحة تماماً.كما ظهرت مئات الأعمال الفنية المعاصرة المكوّنة من كرات بسيطة، بعضها معلَّق في سقف إحدى الصالات الفنية كما هو الحال في «مركز هونف فوف» في ميونيخ بألمانيا، وبعضها موضوع في الأماكن العامة كما هو الحال أمام «متحف مارتا» في هيرفورد بألمانيا أيضاً، أو كالكرة التي صاغها الفنان إريك بريدي لحديقة الفاتيكان. ونتيجة لتطور فن التصميم الطباعي خلال القرن الماضي بات هناك مئات الفنانين المتخصصين في رسم الكرة الأرضية بأساليب تعبيرية وجمالية، تأتي الدقة الجغرافية في آخر اهتماماتها.[ِ 6]
حين يكون المؤتمِرون من رتبة واحدة، كرؤساء الدول مثلاً، أو الوزراء النظراء من بلدان مختلفة، فلا تُستعمل الطاولة المستطيلة. إذ أن الطاولة المستديرة ترمز إلى المساواة وطلب الصلح ومضادة للطبقية. ويُعتقد أن هذا الترميز يعود إلى الملك البريطاني آرثر حين ساوى بين الفرسان الذين التمّوا حول محيط الطاولة في عاصمته كاميلوت. إلا أن وينستون تشيرشل حاول إبطال هذا المفهوم بقوله: «أينما أجلس يكون رأس الطاولة».[ِ 6]
في 1655م، استلهم عالِم الرياضيات البريطاني جون وليس رمزاً للإشارة إلى اللانهائية، وهو دائرة منبعجة يحولها إلى دائرتين مرسومتين بخط واحد، يشبه الرقم 8 المقلوب. ومن رمزيته العلمية إلى الأرقام اللامتناهية، استمدَّ هذا الشكل رمزية أخرى، فأصبح اليوم أيضاً شكلاً فنياً، اعتمده كثير من المصمِّمين لصياغة حلي على سبيل المثال ترمز إلى ديمومة العلاقات.[ِ 6]
استخدمت الدائرة في خلق التجانس الزخرفي مع الخط العربي بشكل مكثف بين الخطوط والأشكال.[ِ 9][ِ 5] تُرسم النجوم في الزخارف العربية مُشتقةً من الدائرة وبأخذ مقاييسها. يذكر أبو حیان التوحیدي: «وأما الصورة الفلكیة فداخلة تحت الرسم بالعرض، وللوهم فیها أثر كبیر، ولأنها مأخودة من الجسم الأعظم صارت مشاكهتها مقسومة بین البسیط الذي لا تركیب فیه البتة، وبین المركب الذي لا یخلو من التركیب البتة.». وقد ابتكر المسلمين العرب الصفر على هيئة الدائرة للدلالة على دورها التولیدي في حساب الأرقام. يرى كثيرون أن في الدائرة عاملُ جذبٍ قويّ للعين، استدلالاً على كثرة استعمالها في علامات السلع التجارية وترويجات التخفيضات وغيرها.[ِ 9]
التطبيقات والاستعمالات

الدولاب هو قرص مستدير يُصنع من مادة صلبة ويُستعمل بشكل شائع في العربات للتنقل. ويُصنّف باحثون على أنَّ اختراع الدولاب من أهم ما اخترع البشر، إذ أنه أدى إلى تطوّرهم العلمي والتكنولوجي. وُجد أقدم دولاب بين الآثار الباقية من التاريخ، بعمر يصل إلى 3,000 سنة. كما احتوت النقوش السومرية والفرعونيّة رسوماً لعربات بدواليب، عمرها 5000 سنة. ويُرجح أن الحيّاكين والنسّاجين والخزّافين وصانعي الفخّار والآجرّ، كانوا من أوائل من استعمل الدولاب في مهنتهم.[ِ 6]
إن الأوعية الفخّاريّة التي كان الخزّافون يصنعونها، كانت ضرورية لخزن الماء والمشروبات وحتى الحبوب وغيرها من الأغذية، في المستقرّات الزراعية التي نشأت من حولها القرى والمدن الأولى. وكانت تعتمد آنية الفخّار على أساسٍ طيني على شكل قرص، والذي يديره الخزّاف لصنع آنيته. ومن هذه الدواليب الأولى، طوّر البشر شيئاً فشيئاً صناعة الدولاب، إلى أطر العجلات والعربات ثم المركبات فالسيارات. كما أن الدائرة كانت الأساس للمحرك الكهربائي والمراوح وبقية المحركات الأخرى.[ِ 6]
معرض صور
براهين وعلاقات
-
مساحة الدائرة تساوي: × مساحة المربع الملون. يُوضّح هذا الرّسم أن مساحة الدّائرة ينبغي -قطعاً- أن تكون أقل من .
-
رسم توضيحي لمثلث في المستوى ، مع أبرز دوائره الخاصة. تُشير النقاط إلى مراكز المثلث الرئيسة، ويُسمَّى الخطُ الواصل بينهم بخط أويلر. النقطة هي نقطة تقاطع ارتفاعات المثلث. النقطة هي مركز دائرة النقاط التسع. النقطة هي نقطة تقاطع متوسطات المثلث. النقطة هي مركز الدائرة المحيطة بالمثلث.
-
هلِالا الحسنِ ابنِ الهيثم: مجموع مساحة الهلالين (بالأزرق) مُساوٍ لمساحة المثلث الأخضر.
-
حالات أزواج الدوائر المُختلفة.
-
القيم الشهيرة المُرتبطة بدائرة الوحدة.
-
إنشاء خماسي منتظم باستعمال الفرجار والمسطرة.
-
الزوايا التي يصنعها مماس الدائرة المحيطة لمثلثٍ عند رأسه
-
مُقاربة لتسمية بعض المصطلحات المتعلقة بالدائرة بأسمائها؛ كالقوسِ والوَتر وعمق القوس، ونقطة المنتصف.
-
حالات الزوايا بالنسبة لدائرة.
-
الزوايا المماسية والمركزية والخارجة عن رباعي دائري.
-
الشكل الحقيقي لزوج من المقاطع الدائرية لمخروط إهليجي في الإسقاطات العمودية
الترميز الموحد
| العلامة | تمثيل اليونيكود البرمجي:(Hex) | بالإنجليزية |
|---|---|---|
| ○ | U+25CB | WHITE CIRCLE |
| ● | U+25CF | BLACK CIRCLE |
| ◯ | U+25EF | LARGE CIRCLE |
| ◌ | DOTTED CIRCLE | |
| ◍ | CIRCLE WITH VERTICAL FILL | |
| ◎ | BULLSEYE | |
| ◉ | FISHEYE |
في الأعلام والرموز
-
علم كوريا الجنوبية.
-
شعار الألعاب الأولمبية.
-
شعار ماستركارد إحدى الشعارات التي يظهر فيه استخدام الدَّائرة بوضوح.
-
شعار تويتر مُنشأ بالكامل من مناطق محصورة بين دوائر.
في اللغات والثقافة
-
رسم مأخوذ من مخطوطة آيسلنديَّة تعود إلى حوالي عام 1750م، ويوضح نموذج مركزية الأرض.
-
تُرسم دائرة صغيرة فوق الحُروفِ العربيَّة للتعبير عن سكون الحرف.
-
تستعملُ اللغةُ اليابانيَّةُ الدَّائرة لتفخيم أو تغيير نطق بعض المقاطع الصّوتية برسمها فوقها. كما أنها تستعمل الدَّائرة كنقطة نهاية السَّطر (。 )
-
تُستعمل الدَّائرة فوق الحروف اللاتينية لبعض اللغات الأوروبيَّة مثل النّرويجية، السُّويديَّة والفنلنديَّة.
-
الصِّفر 0 وحرف الـO من حروف الأبجدية اللاتينية من الحروف المُتناظرة والشبيهة جداً بالدائرة.
-
تتميز اللغة الكورية عن غيرها من بقية اللغات الشرق آسيوية بأن حروف أبجديتها تحوي أشكال بيضاوية ودوائر.
-
الماروجيروشي (باليابانية: 丸印) أو الغونجبو (بالكورية: 공표, 空標)، هي اسم للرمز "◯" المستعمل للدلالة على الإيجاب والموافقة في شرق آسيا، وهي مشابهة في استخدام علامة الصح. عكسها هو علامة الشطب ("✗") أو ("×").
-
لعبة إكس-أوه من الألعاب التي تتضمن شكل الدائرة.
-
علامة اليين واليانغ ترمز لكيفية عمل الأشياء في العلم الصيني القديم.
في التقنية والعلوم
-
تّقنيَّاً، الشّكل الدائري للعجلة يُمكّنها من الحركة الدّورانية.
-
الساعات من الأمثلة الشائعة في الحياة اليومية عن توظيف الشكل الدائري في الأشياء المتكررة.
-
التروس هي العناصر الأساسية والبسيطة للحركة في الهندسة الميكانيكية.
-
المراوح تأخذ الشكل الدائري لأنه الشكل الذي تتخذه المُحركات.
-
مُحرِّكات الطيارات دائرية الشكل.
-
الشكل الدائري للكاميرا يُمكِّنها من التقاط الضوء من نواحٍ متعددة.
-
العدسات المقعرة والمُحدّبة تصنع في الغالب على قوالب دائرية.
-
عوامات السباحة تصنع بشكل دائري لتوزيع قوة الطفو على جميع أنحاء الجسم وسهولة تعلقه فيها.
-
تُصنع أغطية المجاري وغيرها بالشَّكل الدَّائري لتوزيع الضّغط. (انظر: إجهاد اسطوانة).
-
ترمز الدائرة إلى انقطاع التيار الكهربائي في مقاليد الأجهزة الإلكترونية.
-
تطور مقود السيارة في فترات مختلفة.
-
تُستعمَلُ الدَّائرةُ كرمز لقياس درجة الحرارة في أغلب المعايير الحراريَّة، منها: الدَّرجة المئويَّة (°C)، والفهرنهايت (°F) والدليزل (°D) والنيوتن (°N) والرومير (°Ré) والرومر (°Rø) والودجوود (°W).
-
يُشار لقياس الزَّوايا والأقواس الدَّائريَّة بدائرة صغيرة وتُنطق: «درجة».
-
في نظام الإحداثيَّات الجُغرافيَّة، تُصنَّف خطوط الطُّول ودوائر العرض بالنَّسبة لبعدها عن خط الاستواء، ويُقاس كُلّ منها بالدرجة التي يرمز لها بالدَّائرة.
-
تُستعمل الدّرجة لقياس تركيز الكحول وتُرسم دائرةً.
-
تُستخدم الدَّوائر لتمثيل علاقات ڤن في نظرية المجموعات.
-
علامة النسبة المئوية «%» تُستخدم للتعبير عن عدد على شكل كسر من مئة.
في العمارة والفنون
-
قبة زجاجية في إحدى مطاعم مدينة باريس.
-
برج طغرل من الدّاخل.
-
قطعة دائريَّة من الحرير مع نقوش منغوليَّة.
-
تتخذ الدوارات المرورية الشكل الدائري المتناظر لتنظيم عملية سير السيارات.
-
دوائر في لوحة فن تجريدي للفنان روبرت ديلواني.
-
طبق أثري يعود تاريخه إلى القرن الثالث عشر الميلادي في متحف شانغهاي.
-
عجلات ملاهي الألعاب ليلاً.
-
زخرفة إسلامية على شكل دائرية لجملة "يا غفَّار".
-
لوحة الفلكي للفنان يوهانس فيرمير.
-
لوحة مربعات في دوائر متعرجة للفنان فاسيلي كاندينسكي.
-
لوحة دوائر في دائرة للفنان فاسيلي كاندينسكي.
-
لوحة عدة دوائر للفنان فاسيلي كاندينسكي.
في الطَّبيعةِ
-
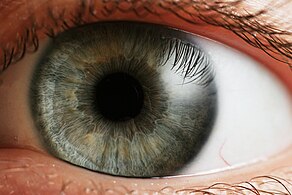
عين إنسان.
-
كريات الدَّم الحمراء هي المسؤولة عن نقل الغذاء والأكسجين لأجهزة الجسم.
-
فوّهة تايكو، واحدة من الأمثلة المتعددة التي تظهر فيها الدوائر في الطبيعة.
-
الشكل الكامل لقوس المطر هو دائرة كاملة، ويُسمَّى الجُزءُ الَّذي يُمكنُ رؤيتهُ منها فوق الأفق قوساً.
-
هالة الشَّمس أثناء الكسوف الكُلِّي.
-
الشَّمس، واحدة من بلايين الأجرام السَّماويَّة التي تظهر بشكل القرص الدَّائريّ.
-
دوائر المحاصيل تحدث عند دهس حقل من المحاصيل، وقد استخدمت للترويج.
-
الموجات الناتجة على سطح الماء دائريَّة.
-
حلقة تكونت بفعل نمو الفطريات.
-
الحلزون أبيض الطرف هو نوع من الحلزونات البرية الشائعة في أوروبا.
-
تباع الشمس هي نبتة بذور زيتية.
انظر أيضًا
| دائرة في المشاريع الشقيقة: | |
- قائمة المواضيع المتعلقة بالدائرة.
- علامة O.
- حلقة
- كرة
- مخروط.
- قطع ناقص أو الشكل البيضاوي.
- بيضاوي ديكارتي.
- قطع مكافئ.
- قطع زائد.
- مثلث.
- حساب مثلثات.
دوائر خاصة
في مثلث
- دائرة داخلية.
- دائرة خارجية.
- دائرة محيطة.
- دائرة محيطة بمثلث قائم.
- دائرة النقاط التسع.
- دائرة ليستر.
- دائرة مالفاتي.
- دائرة بروكار.
في أشكال أخرى
ملاحظات
- ^ في بعض الكُتب يُذكر هذا التّعريف نفسه، مع تقليل المصطلحات لمراعاة المرحلة الدّراسية التي يستهدفها الكتاب. كالتعريف الآتي على سبيل المثال: "الدائرة: هي مجموعة نّقاط على مستوى تبعد البعد ذاته من نقطة ثابتة ما، هي مركز الدّائرة". هذا المحل الهندسي من النّقاط هو مجموعة غير منتهية.
- ^ يُشتَرط لنصف قطر الدائرة أن يكون عدداً حقيقيَّاً موجباً. إلا أن هناك فروع في الهندسة من تُعيد هذا التعريف ليشمل الأعداد الحقيقية السالبةَ أيضاً، مثل الإحداثيات القطبية.
- ^ يُسمّى المركز نقطة المنتصف أو النّقطة المركزية أيضاً. والترميز O جاء من اللاتينية: Origin بمعنى نقطة الأصل. بينما M من الإنجليزية: Midpoint والتي تعني نقطة المنتصف. بينما جاء الترميز العربي للمصطلح من كلمة «مركز».
- ^ من اللاحقة اللاتينية: Circum- والتي تعني يُحيط. ويُقرأ مُحيط الدَّائرة . بينما جاء الترميز العربي من أول حرفين من كلمة «محيط».
- ^ من اللاتينيّة: Area أي: قطعة مستوية وفارغة من مستوى الأرض. بينما جاء الترميز العربي بأخذ أول حرف من «مساحة».
- ^ من اللاتينية: Radius بمعنى شعاع. بينما جاء الترميز العربي من حروف البداية لكلمتي «نصف قطر»
- ^ من اللاتينية المأخوذة من الإغريقية: Diagonios بمعنى من زاوية إلى زاوية (القطر). بينما جاء الترميز العربي من أول حرف من كلمة «قطر»
- ^ نصف القرص هو حالة خاصة من القطعة، ويُعرف أيضاً بأنه أكبر قطعة في الدائرة.
- ^ لاحظ أن تعريف الدّائرة ينص على أنّها "مجموعة نقاط".
- ^ يُعرف نصف القطر المماسي لمضلع منتظم على أنه البعد بين مركز المضلع المنتظم وأحد أضلاعه. (انظر أيضاً: مسافة بين نقطة وخط)
- ^ يُعرف نصف القطر المحيطي لمضلع منتظم على أنه البعد بين مركز المضلع المنتظم وأحد رؤوسه.
- ^ القطر هو حالة خاصّة من الوتر، حيث ينطبق عليه نفس تعريف الوتر ويُمكن القول بإنّ القطر هو أطول وتر ممكن في الدّائرة. يُرمز للقطر بـ"ق" أو "2 نق" حيث أن طوله ضعف طول الشّعاع.
- ^ القياس يكون عبر إحاطة مُحيط الدائرة بخيط ثُمّ قياس طوله بعد فرده مستقيماً لاحقاً.
- ^ يُقرأً پاي.
- ^ الزاوية الداخلية هي عكس الزاوية المُنعكسة. (انظر أيضاً: زاوية)
- ^ سُمِّيت بذلك لأن رأسها يقع على نقطةَ المركز.
- ^ سُمِّيت بذلك لأن رأسها يقع على محيط الدائرة وتحصر جزءاً منه.
- ^ سُمّيت بذلك بسبب انحصارها بين وتر وومماس على الدائرة.
- ^ هو ترميز لمجموعة النقاط الداخلية. وهو اختصار للكلمة الإنگليزيَّة: والتي تعني داخليّ.
- ^ هو ترميز لمجموعة النقاط الخارجية. وهو اختصار للكلمة الإنگليزيَّة: والتي تعني خارجيّ.
- ^ أي: إما أن تكون حادة أو قائمة.
- ^ أ ب ت المسافة بين نُقطة ومُستقيم تُعرف بأنها المسافة العموديّة بين النّقطة والمُستقيم. وتُقاس بقياس طول العمود السّاقط من النقطة على المستقيم، ويُرمز للمسافة بين نقطةٍ ما ومستقيم ما بـ. (انظر أيضاً: مسافة بين نقطة وخط)
- ^ أو يقطع الدائرة في نقطة واحدة.
- ^ لاحظ أن طول قطر الدائرة ثابت ويساوي وأن أي وتر آخر لا يمثل قطراً فإن طوله أصغر من قطر الدائرة.
- ^ تشير إلى دالة السهم
- ^ أو يُعبَّر عنه أحياناً بـ: ثلاث نقاط ليست على استقامة واحدة.
- ^ تتضمن الدوائر الماسة للمثلث الدوائر الداخلية والخارجية.
- ^ أو بشكلٍ مُكافئ، وُجدت نُقطة داخل الرُّباعي بحيث تبعد بعداً متساوٍ عن رؤوسه.
- ^ الرمز يُشير إلى «تقاطع».
- ^ إشارةُ مركز التشابهِ هي كما سبق ذكره: موجبةٌ لمركز التشابه الخارجي، وسالبة لمركز التشابه الداخلي.
- ^ ويطلق عليها أيضاً اسمَ الدائرة المثلثية
- ^ عكس اتجاه عقارب الساعة لأجلِ زاويةٍ موجبةٍ ، وفي اتجاه عقارب الساعة من أجل زاويةٍ سالبةٍ .
- ^ ويُطلق عليها اسم «معادلة بارامترية» أيضاً (بالإنجليزية: Parametric equation).
- ^ وهو في الواقع ضعف طول القطر أي ما يُساوي تقريباً 3.14 ضعف طول القطر، وهو تقدير قريب نوعاً ما نسبةً إلى ذلك الزّمن.
المراجع
باللغة العربية
- ^ أ ب ت ث ج ح خ د ذ ر ز أديب، عادل نسيم (1 يناير 2009). الهندسة التحليلية. المنهل. ISBN:9796500139289. مؤرشف من الأصل في 2020-03-12.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ أ ب ت ث ج ح خ د ذ ر ز س ش ص ض ط ظ ع غ ف ق سمحان، معروف؛ التويجري، نجلاء؛ توبان، ليانا (1437هـ/2016م). رياضيات الأولمبياد - مرحلة الإعداد: الهندسة (ط. الأولى). الرياض: العبيكان للنشر. ISBN:978-603-503-866-9. مؤرشف من الأصل في 2020-03-07. اطلع عليه بتاريخ 6 سبتمبر، 2017م..
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=و|تاريخ=(مساعدة) ويحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ أ ب ت ث ج ح خ د ذ ر ز س ش صابر، طارق؛ أندريكا، دورين (1434هـ). رياضيَّات الأولمبياد، الهندسة، الجزء الأول. مؤرشف من الأصل في 2019-12-18. اطلع عليه بتاريخ 21 سبتمبر، 2018م.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة)،|موقع=تُجوهل (مساعدة)، ويحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ أ ب ت ث ج ح خ كتاب الأصول لإقليدس، ترجمة: الطوسي، نصير الدين محمد بن محمد، 1201-1274 نسخة محفوظة 23 مارس 2019 على موقع واي باك مشين.
- ^ أ ب ت ث ج ح خ د العلاقة التكاملية بين التكوينات الرمزية والأبعاد الرياضية الهندسية للدائرة في الفن التشكيلي، جبريل, جمال الدين محجوب الجاك; مشرف, -سليمان يحي محمد نسخة محفوظة 11 مارس 2020 على موقع واي باك مشين.
- ^ أ ب ت ث ج ح القافلة، فريق. "الدائرة | مجلة القافلة". مؤرشف من الأصل في 2018-02-10. اطلع عليه بتاريخ 2020-03-12.
- ^ أ ب ت ث "الدوائر (العام الدراسي 8, الهندسة والوحدات) – Matteboken". Matteboken. مؤرشف من الأصل في 2017-09-05. اطلع عليه بتاريخ 2017-09-05.
- ^ أ ب ت ث ج ح خ د ذ ر ز س ش ص ض ط ظ ع غ ف ق سعيد سعد الفهمي الزهراني (2013). المرجع في أولمبياد الرياضيات. مطابع الحميضي. ISBN:9786030112494.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ أ ب ت "الرموز الهندسية نموذج الدائرة ومداها المفاهيمي في التجربة التشكيلية". دنيا الرأي. مؤرشف من الأصل في 2020-03-11. اطلع عليه بتاريخ 2020-03-11.
بلغات أجنبية
- ^ أ ب "Circle definition with calculator - Math Open Reference". www.mathopenref.com. مؤرشف من الأصل في 2019-09-06. اطلع عليه بتاريخ 2020-03-11.
- ^ "Conic section - circle - Math Open Reference". www.mathopenref.com. مؤرشف من الأصل في 2019-08-21. اطلع عليه بتاريخ 2020-03-12.
- ^ "Simple proofs: Archimedes' calculation of pi « Math Scholar". mathscholar.org. مؤرشف من الأصل في 2019-08-22. اطلع عليه بتاريخ 2020-03-12.
- ^ "Approximating Pi — NOVA | PBS". www.pbs.org. مؤرشف من الأصل في 2019-07-24. اطلع عليه بتاريخ 2020-03-12.
- ^ approximated 2π to 9 sexagesimal digits. Al-Kashi, author: Adolf P. Youschkevitch, chief editor: Boris A. Rosenfeld, p. 256 O'Connor، John J.؛ Robertson، Edmund F.، "Ghiyath al-Din Jamshid Mas'ud al-Kashi"، تاريخ ماكتوتور لأرشيف الرياضيات. Azarian, Mohammad K. (2010), "al-Risāla al-muhītīyya: A Summary", Missouri Journal of Mathematical Sciences 22 (2): 64–85.
- ^ "A Brief History of Pi (π)". Exploratorium (بEnglish). 23 Jan 2017. Archived from the original on 2020-02-24. Retrieved 2020-03-12.
- ^ Fraser, Craig G. – The Cosmos: A Historical Perspective (2006) – p.14
- ^ Lawson، Russell M. (2004). Science in the Ancient World: An Encyclopedia. أي بي سي-كليو. ص. 29–30. ISBN:1851095349.
{{استشهاد بكتاب}}: صيانة الاستشهاد: ref duplicates default (link) - ^ أ ب Jean-François Charnier, "The Circle from East to West", The Louvre Abu Dhabi: A World Vision of Art, October 29, 2019 نسخة محفوظة 12 مارس 2020 على موقع واي باك مشين.
- ^ أ ب Davis, P.J. (2006). Mathematics & Common Sense: A Case of Creative Tension. CRC Press. ISBN 978-1-4398-6432-6. Archived from the original on 29 March 2019. Retrieved 2019-01-15. نسخة محفوظة 12 مارس 2020 على موقع واي باك مشين.
- ^ أ ب Ball, W.W. Rouse (1960). A Short Account of the History of Mathematics (4th ed. [Reprint. Original publication: London: Macmillan & Co., 1908] ed.). New York: Dover Publications. pp. 50–62. ISBN 0-486-20630-0.
- ^ أ ب Azad, H., and Laradji, A., "Some impossible constructions in elementary geometry", Mathematical Gazette 88, November 2004, 548–551.
- ^ أ ب ت ث ج "Geometry - Circles and Angles". Malin Christersson's Math Site (بEnglish). Archived from the original on 2019-09-11. Retrieved 2020-03-12.
- ^ Muḥammad ibn Mukarram Ibn (1997). لسان العرب. دار بيروت للطباعة والنشر،. مؤرشف من الأصل في 2020-03-12.
- ^ krikos نسخة محفوظة 2013-11-06 على موقع واي باك مشين., Henry George Liddell, Robert Scott, A Greek-English Lexicon, on Perseus
- ^ Ilia Nikolaevich Bronštein: Taschenbuch der Mathematik. Verlag Harri German, 5th edition, Thun and Frankfurt 2001, p. 143.
- ^ Arnold، B. H. (2013)، Intuitive Concepts in Elementary Topology، Dover Books on Mathematics، Courier Dover Publications، ص. 58، ISBN:9780486275765، مؤرشف من الأصل في 2020-03-11.
- ^ "What Is Circle?". www.cut-the-knot.org. مؤرشف من الأصل في 2019-08-21. اطلع عليه بتاريخ 2020-03-12.
- ^ Harkness, James (1898). "Introduction to the theory of analytic functions". Nature. ج. 59 ع. 1530: 30. Bibcode:1899Natur..59..386B. DOI:10.1038/059386a0. مؤرشف من الأصل في 2009-03-07.[وصلة مكسورة]
- ^ أ ب ت ث Ogilvy, C. Stanley , Excursions in Geometry, Dover, 1969, 14–17.
- ^ Altshiller-Court, Nathan, College Geometry, Dover, 2007 (orig. 1952).
- ^ Courant and Robbins 1996, p. 172; Durell 1928, p. 73
- ^ Weisstein, Eric W. "Cross Ratio". mathworld.wolfram.com (بEnglish). Archived from the original on 2018-11-02. Retrieved 2020-03-12.
- ^ أ ب ت ث H. S. M. Coxeter and S. L. Greitzer.Geometry revisited, volume 19 ofNew MathematicalLibrary. Random House, Inc., New York, 1967.
- ^ أ ب Complex analysis : an introduction to the theory of analytic functions of one complex variable (ط. 3d ed). New York: McGraw-Hill. 1979. ISBN:0-07-000657-1. OCLC:4036464. مؤرشف من الأصل في 2020-03-13.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (مساعدة) - ^ The Associated Harmonic Quadrilateral, Paris Pamfilos, Forum Geometricorum, Volume 14 (2014) 15–29.
- ^ Hans Schwerdtfeger, Geometry of Complex Numbers, Courier Dover Publications, 1979
- ^ Michael Henle, "Modern Geometry: Non-Euclidean, Projective, and Discrete", 2nd edition, Prentice Hall, 2001
- ^ Weisstein, Eric W. "Degenerate". mathworld.wolfram.com (بEnglish). Archived from the original on 2019-07-30. Retrieved 2019-11-29.
- ^ "The Most Marvelous Theorem in Mathematics". www.maa.org. مؤرشف من الأصل في 2017-06-24. اطلع عليه بتاريخ 2020-03-12.
- ^ أ ب ت ث ج ح خ د ذ ر ز Weisstein, Eric W. "Circle". mathworld.wolfram.com (بEnglish). Archived from the original on 2019-07-30. Retrieved 2020-03-11.
- ^ O'Connor، John J.؛ Robertson، Edmund F.، "Cartesian Oval"، تاريخ ماكتوتور لأرشيف الرياضيات
- ^ Encyclopaedia of mathematics : an updated and annotated translation of the Soviet "Mathematical encyclopaedia". Dordrecht: Reidel. ©1988-©1994. ISBN:1-55608-010-7. OCLC:16755499. مؤرشف من الأصل في 2020-03-13.
{{استشهاد بكتاب}}: تحقق من التاريخ في:|تاريخ=(مساعدة) - ^ Burago (2001) [1994], "Isoperimetric inequality", in Hazewinkel, Michiel (ed.), Encyclopedia of Mathematics, Springer Science+Business Media B.V. / Kluwer Academic Publishers, ISBN 978-1-55608-010-4
- ^ أ ب ت ث ج ح خ K.، المحرر (31 يناير 1882). Steiner, Jacob: Gesammelte Werke. Band 2. Berlin, New York: DE GRUYTER. ISBN:978-3-11-161171-6. مؤرشف من الأصل في 2018-06-28.
{{استشهاد بكتاب}}:|archive-date=/|archive-url=timestamp mismatch (مساعدة) - ^ أ ب ت Blåsjö, Viktor (2005). "The Evolution of the Isoperimetric Problem". Amer. Math. Monthly. 112 (6): 526–566. doi:10.2307/30037526. JSTOR 30037526.
- ^ أ ب ت "The Unit Circle Deformed". students.rockefeller.edu. مؤرشف من الأصل في 2019-08-26. اطلع عليه بتاريخ 2020-03-12.
- ^ أ ب ت "p-norm in nLab". ncatlab.org. مؤرشف من الأصل في 2019-03-25. اطلع عليه بتاريخ 2020-03-12.
- ^ أ ب Max Koecher, Aloys Krieg: Ebene Geometrie. 3. Auflage. Springer, Berlin Heidelberg New York 2007, ISBN 978-3-540-49327-3, S. 143.
- ^ "IXL | Similarity of circles | Geometry math". IXL Learning (بen-US). Archived from the original on 2015-09-19. Retrieved 2020-03-12.
{{استشهاد ويب}}: صيانة الاستشهاد: لغة غير مدعومة (link) - ^ Katz، Victor J. (1998)، A History of Mathematics / An Introduction (ط. 2nd)، Addison Wesley Longman، ص. 108، ISBN:978-0-321-01618-8، مؤرشف من الأصل في 2020-03-07
- ^ Andrews، George E.؛ Askey، Richard؛ Roy، Ranjan (1999). Special Functions. مطبعة جامعة كامبريدج. ص. 58. ISBN:978-0-521-78988-2.
- ^ Gupta، R.C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati. ج. 14 ع. 1–4: 68–71.
- ^ πe trillion digits of π نسخة محفوظة 6 December 2016 على موقع واي باك مشين.
- ^ Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes’ constant on Google Cloud نسخة محفوظة 19 أكتوبر 2019 على موقع واي باك مشين.
- ^ Weisstein, Eric W. "Arc". MathWorld.
- ^ "معلومات عن قطاع دائري على موقع bigenc.ru". bigenc.ru. مؤرشف من الأصل في 2019-12-12.
- ^ Gerard, L. J. V., The Elements of Geometry, in Eight Books; or, First Step in Applied Logic (London, Longmans, Green, Reader and Dyer, 1874), p. 285.
- ^ أ ب ت ث ج ح خ Stefan Lozanovski. A Beautiful Journey Through Olympiad Geometry (بالإنجليزية). Archived from the original on 2019-08-22.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(help)صيانة الاستشهاد: لغة غير مدعومة (link) - ^ شتاينر (1826). "Einige geometrische Betrachtungen". Journal für die reine und angewandte Mathematik 1: 161–184.
- ^ داربو، غاستون (1872). "Sur les relations entre les groupes de points, de cercles et de sphéres dans le plan et dans l’espace". Annales Scientifique de l'École Normale Superieure 1: 323–392.
- ^ Coxeter، H. S. M. (1969). Introduction to Geometry (الطبعة 2nd). New York: Wiley.
- ^ أ ب "Tangent Circles". whistleralley.com. مؤرشف من الأصل في 2019-08-15. اطلع عليه بتاريخ 2020-03-12.
- ^
Eric W. Weisstein (2007). "circle - circle intersection" (بEnglish). Archived from the original on 19 يونيو 2019. Retrieved 24/12/2019.
{{استشهاد ويب}}: تحقق من التاريخ في:|تاريخ الوصول=(help) - ^ أ ب ت ث Coxeter, H. S. M. "Inversion in a Circle" and "Inversion of Lines and Circles." §6.1 and 6.3 in Introduction to Geometry, 2nd ed. New York: Wiley, pp. 77-83, 1969.
- ^ أ ب Euclid (9 May 2013). The Thirteen Books of the Elements (بEnglish). Courier Corporation. ISBN:9780486157290. Archived from the original on 2020-03-07.
- ^ Pedoe, D. (1995). "Circles: A Mathematical View, rev. ed". Washington, DC: Math. Assoc. Amer.
- ^ Weisstein, Eric W. "Lens". mathworld.wolfram.com (بEnglish). Archived from the original on 2019-07-30. Retrieved 2020-03-12.
- ^ Postnikov، M. M. (2000)، "The problem of squarable lunes"، الرياضيات الأمريكية الشهرية، ج. 107، ص. 645–651، DOI:10.2307/2589121، JSTOR:2589121. Translated from Postnikov's 1963 Russian book on نظرية غالوا.
- ^ Heath، Thomas L. (2003)، A Manual of Greek Mathematics، Courier Dover Publications، ص. 121–132، ISBN:0-486-43231-9، مؤرشف من الأصل في 2023-02-27.
- ^ James، Robert C.؛ James، Glenn (1992). Mathematics Dictionary (ط. Fifth). Chapman & Hall. ص. 436. مؤرشف من "unit%20complex%20number"&pg=PA436#v=onepage&q="unit%20complex%20number"&f=false الأصل في 2019-12-31.
- ^ Woodward، Ernest (ديسمبر 1978). Geometry - Plane, Solid & Analytic Problem Solver. Problem Solvers Solution Guides. Research & Education Association (REA). ص. 359. ISBN:978-0-87891-510-1. مؤرشف من الأصل في 2020-03-11.
- ^ Chakerian, G. D. (1979). "7". In Honsberger, R. (ed.). A Distorted View of Geometry. Mathematical Plums. Washington, DC, USA: Mathematical Association of America. p. 147.
- ^ Mottola, R. M. "Liutaio Mottola Lutherie Information Website". Liutaio Mottola Lutherie Information Website (بEnglish). Archived from the original on 2020-01-05. Retrieved 2020-03-12.
- ^ THE SAGITTA AND ITS APPLICATIONS, Herbert Wertheim College of Engineering; Department of Mechanical & Aerospace Engineering نسخة محفوظة 24 أكتوبر 2018 على موقع واي باك مشين.
- ^ أ ب ت R. A. Johnson (1960). Advanced Euclidean Geometry: An Elementary Treatise on the Geometry of the Triangle and the Circle (ط. reprint of 1929 edition by Houghton Miflin). New York: Dover Publications. ص. 31–43. ISBN:978-0-486-46237-0.
- ^ أ ب Libeskind, Shlomo (2008), Euclidean and Transformational Geometry: A Deductive Inquiry, Jones & Bartlett Learning, p. 21, ISBN 978-0-7637-4366-6/
- ^ أ ب Posamentier, Alfred S., and Lehmann, Ingmar. The Secrets of Triangles, Prometheus Books, 2012.
- ^ Nelson, Roger, "Euler's triangle inequality via proof without words," Mathematics Magazine 81(1), February 2008, 58-61.
- ^ Dragutin Svrtan and Darko Veljan, "Non-Euclidean versions of some classical triangle inequalities", Forum Geometricorum 12 (2012), 197–209. http://forumgeom.fau.edu/FG2012volume12/FG201217index.html نسخة محفوظة 2019-10-28 على موقع واي باك مشين.
- ^ Smith, Geoff, and Leversha, Gerry, "Euler and triangle geometry", Mathematical Gazette 91, November 2007, 436–452.
- ^ Marie-Nicole Gras, "Distances between the circumcenter of the extouch triangle and the classical centers", Forum Geometricorum 14 (2014), 51-61. http://forumgeom.fau.edu/FG2014volume14/FG201405index.html نسخة محفوظة 2019-10-19 على موقع واي باك مشين.
- ^ Altshiller-Court, Nathan, College Geometry, Dover, 2007.
- ^ Altshiller-Court (1925, pp. 103–110)
- ^ Kay (1969, pp. 18,245)
- ^ Casey, John (1886). Nine-Point Circle Theorem, in A Sequel to the First Six Books of Euclid (ط. 4th). London: Longmans, Green, & Co. ص. 58. مؤرشف من الأصل في 2020-03-12.
- ^ Usiskin، Zalman؛ Griffin، Jennifer؛ Witonsky، David؛ Willmore، Edwin (2008)، "10. Cyclic quadrilaterals"، The Classification of Quadrilaterals: A Study of Definition، Research in mathematics education، IAP، ص. 63–65، ISBN:978-1-59311-695-8
- ^ أ ب Bryant، Victor؛ Duncan، John (2010)، "Wheels within wheels"، The Mathematical Gazette، ج. 94، ص. 502–505.
- ^ أ ب Maley، F. Miller؛ Robbins، David P.؛ Roskies، Julie (2005). "On the areas of cyclic and semicyclic polygons" (PDF). Advances in Applied Mathematics. 34 (4): 669–689. doi:10.1016/j.aam.2004.09.008. مؤرشف من الأصل (PDF) في 10 يناير 2020.
- ^ Josefsson، Martin (2011)، "More Characterizations of Tangential Quadrilaterals" (PDF)، Forum Geometricorum، ج. 11، ص. 65–82، مؤرشف من الأصل (PDF) في 2020-03-13.
- ^ Alsina, Claudi and Nelsen, Roger, Icons of Mathematics. An exploration of twenty key images, Mathematical Association of America, 2011, p. 125.
- ^ Wilson, Jim. "Ptolemy's Theorem." link verified 2009-04-08 نسخة محفوظة 15 ديسمبر 2017 على موقع واي باك مشين.
- ^ "Sine, Cosine, and Ptolemy's Theorem". مؤرشف من الأصل في 2018-07-10.
- ^ Euler, Leonhard (1767). "Solutio facilis problematum quorundam geometricorum difficillimorum". Novi Commentarii academiae scientarum imperialis Petropolitanae. ج. 11: 103–123. E325. مؤرشف من الأصل في 2015-04-11.
- ^ "William Wallace (1768 - 1843)" en. مؤرشف من الأصل في 2018-10-01. اطلع عليه بتاريخ 2020-03-15.
{{استشهاد ويب}}: الوسيط غير صالح|script-title=: بادئة مفقودة (مساعدة) - ^ "Gibson History 7 - Robert Simson". 30 يناير 2008. مؤرشف من الأصل في 2016-10-09.
- ^ Todor Zaharinov, "The Simson triangle and its properties", Forum Geometricorum 17 (2017), 373--381. http://forumgeom.fau.edu/FG2017volume17/FG201736.pdf نسخة محفوظة 2019-02-14 على موقع واي باك مشين.
- ^ Biggs، N. L. (1981)، "T. P. Kirkman, mathematician"، جمعية الرياضيات في لندن، ج. 13، ص. 97–120، DOI:10.1112/blms/13.2.97، MR:0608093
- ^ أ ب Pascal 1640, translation Smith 1959، صفحة 326
- ^ أ ب Graham، L. A. (1959). Ingenious Mathematical Problems and Methods. New York: Dover. ISBN:0486205452. مؤرشف من الأصل في 2020-03-17. اطلع عليه بتاريخ 2012-12-01.
- ^ Casey، J. (1866)، "On the Equations and Properties: (1) of the System of Circles Touching Three Circles in a Plane; (2) of the System of Spheres Touching Four Spheres in Space; (3) of the System of Circles Touching Three Circles on a Sphere; (4) of the System of Conics Inscribed to a Conic, and Touching Three Inscribed Conics in a Plane"، Proceedings of the Royal Irish Academy، ج. 9، ص. 396–423، JSTOR:20488927. See in particular the bottom of p. 411.
- ^ Kimberling، Clark (1994)، "Central Points and Central Lines in the Plane of a Triangle"، Mathematics Magazine، ج. 67، ص. 163–187، JSTOR:2690608، MR:1573021.
- ^ Encyclopedia of Triangle Centers نسخة محفوظة April 19, 2012, على موقع واي باك مشين., accessed 2014-10-24.
- ^ A high school teacher in the French countryside (Nantua) according to Ostermann & Wanner 2012، صفحة 94
- ^ Miquel، Auguste (1838)، "Mémoire de Géométrie"، Journal de Mathématiques Pures et Appliquées، ج. 1، ص. 485–487، مؤرشف من الأصل في 2013-02-13، اطلع عليه بتاريخ 2020-03-14
- ^ Wells 1991، صفحة 184 - Wells refers to Miquel's theorem as the pivot theorem
- ^ أ ب Johnson، Roger A. (1929). Modern Geometry. Houghton Mifflin, Boston (republished facsimile by Dover 1960, 2007 as Advanced Euclidean Geometry).
- ^ Casey، J. (1866). "On the Equations and Properties: (1) of the System of Circles Touching Three Circles in a Plane; (2) of the System of Spheres Touching Four Spheres in Space; (3) of the System of Circles Touching Three Circles on a Sphere; (4) of the System of Conics Inscribed to a Conic, and Touching Three Inscribed Conics in a Plane". Proceedings of the Royal Irish Academy. ج. 9: 396–423. JSTOR:20488927.
- ^ Johnson, Roger A., Advanced Euclidean Geometry, Dover Publ., 2007 (orig. 1929).
- ^ Martin Celli, "A Proof of the Butterfly Theorem Using the Similarity Factor of the Two Wings", Forum Geometricorum 16, 2016, 337–338. http://forumgeom.fau.edu/FG2016volume16/FG201641.pdf نسخة محفوظة 2018-04-24 على موقع واي باك مشين.
- ^ أ ب ت Kunkel, Paul (2007), "The tangency problem of Apollonius: three looks" (PDF), BSHM Bulletin: Journal of the British Society for the History of Mathematics, 22 (1): 34–46, doi:10.1080/17498430601148911 نسخة محفوظة 24 مارس 2018 على موقع واي باك مشين.
- ^ Johnson RA (1960). Advanced Euclidean Geometry: An Elementary treatise on the geometry of the Triangle and the Circle. New York: Dover Publications.
- ^ أ ب Weisstein, Eric W. "Inversion". mathworld.wolfram.com (بEnglish). Archived from the original on 2019-12-29. Retrieved 2020-03-11.
- ^ Durell, C. V. "Inversion." Ch. 10 in Modern Geometry: The Straight Line and Circle. London: Macmillan, pp. 105-120, 1928.
- ^ Coxford, Arthur. Trigonometry. ص. 8–12. مؤرشف من الأصل في 2019-11-21.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ Bityutskov, V.I. (7 Feb 2011). "Trigonometric Functions". Encyclopedia of Mathematics (بEnglish). Archived from the original on 2017-12-29. Retrieved 2017-12-29.
- ^ Coxford, Arthur. Trigonometry. ص. 125. مؤرشف من الأصل في 2019-11-21.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ "Clark University". مؤرشف من الأصل في 2017-12-18.
- ^ Weisstein, Eric W. "Circular Functions". mathworld.wolfram.com (بEnglish). Archived from the original on 2017-04-03. Retrieved 2020-03-01.
- ^ "معلومات عن جذور الوحدة (تحليل عقدي) على موقع zthiztegia.elhuyar.eus". zthiztegia.elhuyar.eus. مؤرشف من الأصل في 2019-12-16.
- ^ "معلومات عن جذور الوحدة (تحليل عقدي) على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2018-10-03.
- ^ "معلومات عن جذور الوحدة (تحليل عقدي) على موقع brilliant.org". brilliant.org. مؤرشف من الأصل في 2019-01-14.
- ^ "معلومات عن كرة على موقع babelnet.org". babelnet.org. مؤرشف من الأصل في 2019-12-13.
- ^ "معلومات عن كرة على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2017-04-02.
- ^ "معلومات عن كرة على موقع jstor.org". jstor.org. مؤرشف من الأصل في 2019-05-26.
- ^ Albert 2016، p. 43
- ^ "MathWorld: Cylindric section". مؤرشف من الأصل في 2018-01-15.
- ^ Slaught، H.E.؛ Lennes، N.J. (1919)، Solid Geometry with Problems and Applications (PDF) (ط. Revised)، Allyn and Bacon، ص. 79–81، مؤرشف من الأصل (PDF) في 2019-09-27
- ^ دنكان سومرفيل (1914) Elements of Non-Euclidean Geometry, page 193 via أرشيف الإنترنت
- ^ "Drawing Compass - History, Use and Types". www.historyofpencils.com. مؤرشف من الأصل في 2019-08-24. اطلع عليه بتاريخ 2020-03-07.
- ^ Ammer، Christine. "Square the Circle. Dictionary.com. The American Heritage® Dictionary of Idioms". Houghton Mifflin Company. مؤرشف من الأصل في 2015-09-09. اطلع عليه بتاريخ 2012-04-16.
- ^ Guilbeau، Lucye (1930). "The History of the Solution of the Cubic Equation". Mathematics News Letter. ج. 5 ع. 4: 8–12. DOI:10.2307/3027812. JSTOR:3027812.
- ^ It shows up in Plato's الجمهورية (ق. 380 BC) VII.530
- ^ Lucye Guilbeau (1930). "The History of the Solution of the Cubic Equation", Mathematics News Letter 5 (4), p. 8-12.
- ^ Stewart، Ian. Galois Theory. ص. 75.
- ^ "معلومات عن تثليث زاوية على موقع britannica.com". britannica.com. مؤرشف من الأصل في 2015-09-05.
- ^ "معلومات عن تثليث زاوية على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2019-07-09.
- ^ "معلومات عن تثليث زاوية على موقع id.loc.gov". id.loc.gov. مؤرشف من الأصل في 2019-12-14.
- ^ آرثر كوستلر, The Sleepwalkers: A History of Man's Changing Vision of the Universe (1959)
- ^ برقلس, The Six Books of Proclus, the Platonic Successor, on the Theology of Plato Tr. Thomas Taylor (1816) Vol. 2, Ch. 2, "Of Plato" نسخة محفوظة 13 مارس 2017 على موقع واي باك مشين.
- ^ "Chronology for 30000BC to 500BC". www-history.mcs.st-andrews.ac.uk. مؤرشف من الأصل في 2018-01-23. اطلع عليه بتاريخ 2017-08-14.
- ^ Squaring the circle. History.mcs.st-andrews.ac.uk. Retrieved on 2012-05-03. نسخة محفوظة 20 مايو 2017 على موقع واي باك مشين.
- ^ أ ب ت ث ج ح خ د Christoph J. Scriba, Peter Schreiber: 5000 Jahre Geometrie: Geschichte, Kulturen, Menschen (Vom Zählstein zum Computer). Springer, Berlin, Heidelberg, New York, ISBN 3-540-67924-3.
- ^ أ ب Max Koecher, Aloys Krieg: Ebene Geometrie. Springer, Berlin, Heidelberg, 3. neu bearbeitete und erweiterte Auflage 2007, Korrigierter Nachdruck 2009, ISBN 978-3-540-49327-3, S. 145.
- ^ أ ب بالإنجليزية: Thomas Little Heath : The works of Archimedes, ed. in modern notation, with introductory chapters. University press, Cambridge 1897. Kreismessung: S. 91 ff., Über Spiralen: S. 151 ff., (Digitalisat). نسخة محفوظة 7 نوفمبر 2016 على موقع واي باك مشين.
- ^ Siehe Gericke: Antike und Orient. S. 120 ff.
- ^ یان.پ.هوخندایک؛ امینی، حسن (1392-01-04). "مطالعه مقاطع مخروطی در دوره اسلامی". میراث علمی اسلام و ایران (بفارسی). ج. 3 ع. 2: 86–98. مؤرشف من الأصل في 2020-03-13.
{{استشهاد بدورية محكمة}}: تحقق من التاريخ في:|تاريخ=(مساعدة) - ^ میرابوالقاسمى، سید محمد تقى؛ باقرى، محمد (22 نوفمبر 2003). "رسالهء عبدالرحمان صوفی دربارهء هندسهء پرگاری". مجله تاریخ علم. ج. 1 ع. 1. ISSN:1735-0573. مؤرشف من الأصل في 2017-05-06.
- ^ یان.پ.هوخندایک؛ امینی، حسن (1392-01-04). "مطالعه مقاطع مخروطی در دوره اسلامی". میراث علمی اسلام و ایران (بفارسی). ج. 3 ع. 2: 86–98. مؤرشف من الأصل في 2020-03-13.
{{استشهاد بدورية محكمة}}: تحقق من التاريخ في:|تاريخ=(مساعدة) - ^ عالمزاده، هادی؛ دوستقرین، فاطمه (1387-07-01). "میرزا ابوتراب نطنزی و رویکردی بدیع به مسأله تثلیث زاویه". تاریخ و تمدن اسلامی (بفارسی). ج. 8 ع. 4: 123–140. مؤرشف من الأصل في 2020-03-13.
{{استشهاد بدورية محكمة}}: تحقق من التاريخ في:|تاريخ=(مساعدة)
قراءة موسعة
- الهندسة: دورة تدريبية شاملة (1988م) «بيدو دان». (بالإنجليزية: Geometry: a comprehensive course).
- Hazewinkel، Michiel، المحرر (2001)، "الدائرة"، Encyclopedia of Mathematics، سبرنجر، ISBN:978-1-55608-010-4 (بالإنجليزية)
ملحق: مسرد المصطلحات الإنجليزية
| مَسرد المفردات وفق أقسام المقالة | |
| مصطلحات أساسية | |
| مركز | Center |
| محيط | Circumference |
| مساحة | Area |
| نصف قطر (شعاع) | Radius |
| وتر | Chord |
| قطر | Diameter |
| قوس | Arc |
| قطع وجزئيات | |
| قطاع | Sector |
| قطعة | Circular segment |
| قرص | Disk |
| مصطلحات استعملت في التعاريف | |
| نسبة تبادلية | Cross-ratio |
| دائرة معممة | Generalized circle |
| تأويل لانهائي | Infinite limit |
| حالة حدية | Limitig case |
| قطع مخروطي | Conic secion |
| استيفاء المساحة | Area optimization |
| متباينة المحيط الثابت | Isoperimetric inequality |
| معيار-p | p-norm |
| زوايا | |
| العدد ط | Pi |
| راديان | Radian |
| زاوية مركزية | Centeral angle |
| زاوية محيطية | Inscribed angle |
| زاوية مماسية | Tangential angle |
| زاوية خارجية | External angle |
| زاوية داخلية | Internal angle |
| نقاط | |
| نقطة داخلية | Internal point |
| نقطة محيطيَّة | Circumference point |
| نقطة خارجية | External point |
| قوة نقطة | Power of a point |
| مبرهنة قطع الوتر | Intersecting chord theorem |
| مبرهنة القاطع | Intersecting secants theorem |
| مبرهنة قاطع التماس | Tangent-secant theorem |
| أزواج الدوائر حسب بعدها عن بعضها | |
| دائرتان متباعدتان | Non-intersecting circles |
| دائرتان متقاطعتان | Intersecting circles |
| دائرتان متماستان داخلياً | Internally tangent circles |
| دائرتان متماستان خارجياً | Externally tangent circles |
| أزواج الدوائر حسب مراكزها وأنصاف أقطارها | |
| دائرتان متعامدتان | Orthogonal circles |
| دائرتان متطابقتان | Congruent circles |
| دائرتان متحدتا المركز | Concentric circles |
| دائرتان منطبقتان | coincident circles |
| أشكال مركبة من دوائر | |
| حلقة | Annulus |
| عدسة | Lens |
| مثلث رولو | Reuleaux triangle |
| أربيلوس | Arbelos |
| مستقيمات وأوتار | |
| مستقيم قاطع | Secant line |
| مستقيم مماس | Tangent line |
| مستقيم مار | Non-intersecting line |
| خط التناظر/خط مركزي | Symmetry line/Center line |
| وتر مشترك | Common chord |
| مماس مشترك خارجي | External common tangent |
| مماس مشترك داخلي | Internal common tangent |
| قطعة تماس | Tangency segment |
| محور أساسي | Radical axis |
| عمق القوس أو السهم | Sagitta أو Versine |
| الدائرة في نظرية الزمر | |
| زمرة التناظر | Symmetry group |
| تناظر انعكاسي | Reflection symmetry |
| دوائر مرتبطة بمضلعات | |
| مضلع دائري | Cyclic polygon |
| مضلع مماسي | Tangential polygon |
| دائرة محيطة | Circumcircle |
| دائرة داخلية | Incircle |
| دائرة خارجية | Excircle |
| دائرة النقاط التسع | Nine-point circle |
| دائرة الوحدة | Unit circle |
| مبرهنات وعلاقات أخرى | |
| التحاكي | Homothety |
| التعاكس | Inversion |
| الإحداثيات الخطية الثلاثية | Trilinear coordinates |
| قانون الجيب | Sine law |
| مبرهنة الفراشة | Butterfly theorem |
| مبرهنة يابانية في الرباعي الدائري | Japanese theorem in cyclic quadrilateral |
| الكرة الفائقة | Hypersphere |
| مبرهنة طاليس | Thales theorem |
| مَسرد المفردات الأبجدي | |
| A | |
| حلقة | Annulus |
| أربيلوس | Arbelos |
| قوس | Arc |
| مساحة | Area |
| استيفاء المساحة | Area optimization |
| B | |
| مبرهنة الفراشة | Butterfly theorem |
| C | |
| مركز | Center |
| زاوية مركزية | Centeral angle |
| وتر | Chord |
| قطعة | Circular segment |
| دائرة محيطة | Circumcircle |
| محيط | Circumference |
| نقطة محيطيَّة | Circumference point |
| دائرتان منطبقتان | coincident circles |
| وتر مشترك | Common chord |
| دائرتان متحدتا المركز | Concentric circles |
| دائرتان متطابقتان | Congruent circles |
| قطع مخروطي | Conic secion |
| نسبة تبادلية | Cross-ratio |
| مضلع دائري | Cyclic polygon |
| D | |
| قطر | Diameter |
| قرص | Disk |
| E | |
| دائرة خارجية | Excircle |
| زاوية خارجية | External angle |
| مماس مشترك خارجي | External common tangent |
| نقطة خارجية | External point |
| دائرتان متماستان خارجياً | Externally tangent circles |
| G | |
| دائرة معممة | Generalized circle |
| H | |
| التحاكي | Homothety |
| الكرة الفائقة | Hypersphere |
| I | |
| دائرة داخلية | Incircle |
| تأويل لانهائي | Infinite limit |
| زاوية محيطية | Inscribed angle |
| زاوية داخلية | Internal angle |
| مماس مشترك داخلي | Internal common tangent |
| نقطة داخلية | Internal point |
| دائرتان متماستان داخلياً | Internally tangent circles |
| مبرهنة قطع الوتر | Intersecting chord theorem |
| دائرتان متقاطعتان | Intersecting circles |
| مبرهنة القاطع | Intersecting secants theorem |
| التعاكس | Inversion |
| متباينة المحيط الثابت | Isoperimetric inequality |
| J | |
| مبرهنة يابانية في الرباعي الدائري | Japanese theorem in cyclic quadrilateral |
| L | |
| عدسة | Lens |
| حالة حدية | Limitig case |
| دائرة النقاط التسع | Nine-point circle |
| دائرتان متباعدتان | Non-intersecting circles |
| مستقيم مار | Non-intersecting line |
| O | |
| دائرتان متعامدتان | Orthogonal circles |
| P | |
| معيار-p | p-norm |
| العدد ط | Pi |
| قوة نقطة | Power of a point |
| راديان | Radian |
| R | |
| محور أساسي | Radical axis |
| نصف قطر (شعاع) | Radius |
| تناظر انعكاسي | Reflection symmetry |
| مثلث رولو | Reuleaux triangle |
| S | |
| عمق القوس أو السهم | Sagitta أو Versine |
| مستقيم قاطع | Secant line |
| قطاع | Sector |
| قانون الجيب | Sine law |
| زمرة التناظر | Symmetry group |
| خط التناظر / خط مركزي | Symmetry line/Centerline |
| T | |
| قطعة تماس | Tangency segment |
| مستقيم مماس | Tangent line |
| مبرهنة قاطع التماس | Tangent-secant theorem |
| زاوية مماسية | Tangential angle |
| مضلع مماسي | Tangential polygon |
| مبرهنة طاليس | Thales theorem |
| الإحداثيات الخطية الثلاثية | Trilinear coordinates |
| U | |
| دائرة الوحدة | Unit circle |
وصلات خارجية
- دروس في هندسة الدائرة على منصة إدراك.
- مساحة الدائرة على منصة إدراك.
- كتاب Inventing the circle للكاتب يوهان جيليس.
- الدائرة في أرشيف ماكتوتر لتاريخ الرياضيات.
- "تطبيقات (بُرَيمجات) جافا تفاعلية". مؤرشف من الأصل في 2019-09-07.
لخواص الإنشاءات الأساسية المرتبطة بالدائرة.
- "مسائل ونقاش حول الدائرة". مؤرشف من الأصل في 2019-08-21.
Cut the knot
- "تطبيق تفاعلي لمعادلة الدائرة القياسية". مؤرشف من الأصل في 2019-05-02.
- الدائرة في الهندسة الوصفية. على اليوتيوب.
- الدائرة في الهندسة التحليلية. على اليوتيوب.