سهم (حساب المثلثات)

  لمعانٍ أخرى، طالع سهم (توضيح).

ميز عن قاطع التمام، مقلوب دالة الجيب؛ وقوس الجيب، الدالة العكسية للجيب.

السهم أو الجيب المعكوس (بالإنجليزية: Versed Sine أو Versine)‏ هي دالة مثلثية موجودة في بعض الجداول المثلثية القديمة. سهم زاوية هو فرق بين جيب تمام زاوية نفسها والواحد، بتعبيرٍ آخر: $\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}\theta =1-\cos \theta$

هناك العديد من الدوال ذات الصلة، وأبرزها سهم التمام (Coversine) و نصف السهم (Haversine). هذه الأخيرة، لها أهمية خاصة في صيغة نصف السهم للملاحة.

دائرة الوحدة مع الدوال المثلثية، بين هذا الرسم سبب تسمية دالة السهم.

نظرة عامة

السهم هو عبارة عن دالة مثلثية ظهرت سابقا في بعض الجداول المثلثية القديمة. يرمز إليها بالرموز التالية: versin (θ)، sinver (θ) ، vers(θ)، ver (θ) أو siv (θ). باللغة اللاتينية، يُعرف بالاسماء التالية: sinus versus (جيب معكوس)، versinus ،versus أو sagitta (السهم).

يكافئ سهم الزاوية العبارات التالية: 1 − cos(θ) و 2 sin² (θ/2).

هناك عدة دوال متعلقة بالسهم:

• جيب التمام المعكوس (بالإنجليزية: Versed cosine)‏: يرمز لها بالرمز vercos(θ) أو vcs(θ).
• سهم التمام أو الجيب المعكوس للتمام (بالإنجليزية: Coversed sine)‏: يرمز لها بالرمز coversin(θ)، أو (covers(θ)، أو cosiv(θ) أو cvs(θ).
• جيب التمام المعكوس للتمام (بالإنجليزية: Coversed cosine)‏: يرمز لها بالرمز covercosin(θ) أو covercos(θ) أو cvc(θ).

توجد أيضًا مجموعة أخرى من أربع دوال «نصف القيمة»:

• نصف السهم (بالإنجليزية: Haversine)‏: يرمز إليها بالرمز haversin(θ) أو hav(θ)
• نصف سهم التمام (بالإنجليزية: Hacoversed sine)‏: يرمز إليها بالرمز hacoversin(θ) أو hcv(θ).
• نصف جيب التمام المعكوس (بالإنجليزية: Haversed cosine)‏: يرمز إليها بالرمز havercosin(θ) أو hvc(θ).
• نصف جيب التمام المعكوس للتمام (بالإنجليزية: Hacoversed cosine)‏: يرمز إليها بالرمز hacovercosin(θ) أو hcc(θ).

التاريخ والتطبيقات

السهم وسهم التمام (Coversine)

الجيب وجيب التمام، والسهم للزاوية θ من حيث دائرة الوحدة مع دائرة نصف قطرها 1، مركزها O. كما يوضح هذا الرسم هو السبب في تسمية الدالة بـ «السهم». إذا كان قوس ADB للزاوية المزدوجة Δ = 2θ يُنظر إليها على أنها «قوس المحارب» والقطعة AB كوترها، ومن ثم فإن القطعة المستقيمة CD هو «عمود السهم».

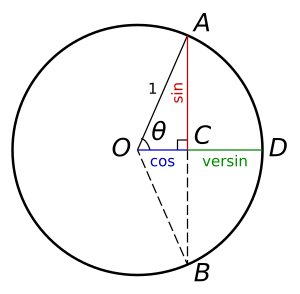
في بعض الأحيان، كانت تسمى تاريخيا دالة الجيب العادية sinus rectus («الجيب المستقيم» بالترجمة الحرفية) للتمييز بينها وبين السهم (sinus versus). يكون معنى هذه المصطلحات واضحًا إذا نظر المرء إلى الدوال في السياق الأصلي لتعريفها، وهي دائرة الوحدة:

بالنسبة للوتر العمودي AB لدائرة الوحدة، يكون جيب الزاوية θ (يمثل نصف الزاوية المقابلة Δ) هو المسافة AC (نصف الوتر). من ناحية أخرى، فإن سهم الزاوية θ هو المسافة CD من مركز الوتر إلى مركز القوس. وبالتالي، فإن مجموع cos (θ) (يساوي طول الخط OC) و versin (θ) (يساوي طول الخط CD) يساوي طول نصف القطر OD (طوله 1). يتضح بهذه الطريقة بأن الجيب عمودي (rectus، حرفيًا «مستقيم») بينما يكون السهم أفقيًا (versus، حرفيًا «مقلوب، خارج الموضع»)؛ كلاهما مسافات من C إلى الدائرة.

كانت التسمية العربية للدالة ترجمة للكلمة الهندية "sara" التي تستخدم للإشارة إلى سهم المحارب. إذا كان القوس ADB للزاوية المزدوجة Δ = 2θ ينظر إليه على أنه «قوس المحارب» واعتبار AB على أنه «وتر»، والسهم CD هو عمود السهم.

نصف السهم (Haversine)

كانت دالة نصف السهم ($\mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}=\frac{\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}x}{2}$) مهمًة خاصة في الملاحة لأنها تظهر في صيغة نصف السهم (Haversine formula)، والتي تستخدم لحساب المسافات بدقة على سطح كروي فلكي (طالع المشكلات المتعلقة بنصف قطر الأرض والشكل الكروي) باعتبار إلى المواضع الزاوية (على سبيل المثال، خط الطول ودائرة العرض). يمكن للمرء أيضًا استخدام ${\sin }^2(\frac{\theta }{2})$ مباشرة، ولكن وجود جدول لنصف السهم أزالت الحاجة إلى حساب المربعات والجذور التربيعية.

المتطابقات الرياضية

التعريفات

$\text{versin}(\theta ):=2{\sin }^2(\frac{\theta }{2})=1-\cos (\theta )$
$\text{coversin}(\theta ):=\text{versin}(\frac{\pi }{2}-\theta )=1-\sin (\theta )$
$\text{vercosin}(\theta ):=2{\cos }^2(\frac{\theta }{2})=1+\cos (\theta )$
$\text{covercosin}(\theta ):=\text{vercosin}(\frac{\pi }{2}-\theta )=1+\sin (\theta )$
$\text{haversin}(\theta ):=\frac{\text{versin}(\theta )}{2}={\sin }^2(\frac{\theta }{2})=\frac{1-\cos (\theta )}{2}$
$\text{hacoversin}(\theta ):=\frac{\text{coversin}(\theta )}{2}=\frac{1-\sin (\theta )}{2}$
$\text{havercosin}(\theta ):=\frac{\text{vercosin}(\theta )}{2}={\cos }^2(\frac{\theta }{2})=\frac{1+\cos (\theta )}{2}$
$\text{hacovercosin}(\theta ):=\frac{\text{covercosin}(\theta )}{2}=\frac{1+\sin (\theta )}{2}$

الدورات الدائرية

$\begin{array}{rr}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(\theta )& =\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\frac{\pi }{2})=\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\pi )=\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\frac{3\pi }{2})\\ \mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(\theta )& =\mathrm{h}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\frac{\pi }{2})=\mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\pi )=\mathrm{h}\mathrm{a}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{c}\mathrm{o}\mathrm{s}\mathrm{i}\mathrm{n}(\theta +\frac{3\pi }{2})\end{array}$

المشتقات والتكاملات

$\frac{\mathrm{d}}{\mathrm{d}x}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(x)=\sin x$	$\int \mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(x)\mathrm{d}x=x-\sin x+C$
$\frac{\mathrm{d}}{\mathrm{d}x}\mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(x)=-\cos x$	$\int \mathrm{c}\mathrm{o}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(x)\mathrm{d}x=x+\cos x+C$
$\frac{\mathrm{d}}{\mathrm{d}x}\mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(x)=\frac{\sin x}{2}$	$\int \mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(x)\mathrm{d}x=\frac{x-\sin x}{2}+C$

خصائص أخرى

يمكن تعبير تلك الدوال بواسطة متسلسلة ماكلورين:

$\begin{array}{rr}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(z)& =\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k-1}{z}^{2k}}{(2k)!}\\ \mathrm{h}\mathrm{a}\mathrm{v}\mathrm{e}\mathrm{r}\mathrm{s}\mathrm{i}\mathrm{n}(z)& =\sum _{k=1}^{\mathrm{\infty }}\frac{(-1{)}^{k-1}{z}^{2k}}{2(2k)!}\end{array}$

طالع أيضًا

• عمق قوس