صيغة نصف السهم

تُحَدِّد صيغة نصف السهم^{[ملاحظة 1]} أو صيغة نصف الجيب المعكوس^{[ملاحظة 1]} (بالإنجليزية: Haversine formula)‏ مسافة الدائرة العظمى بين نقطتين على الكرة المعطاة بخطوط الطول ودوائر العرض. مهمة في الملاحة، إنها حالة خاصة للصيغة الأكثر عمومية في حساب المثلثات الكروية، قانون نصف السهم، الذي يربط جوانب وزوايا المثلثات الكروية.

وقد نشر الجدول الأول لنصف السهم باللغة الإنجليزية من قبل جيمس أندرو في 1805،^[1] ولكن فلوريان كايوري ينسب استخدام سابق إلى جوسيف دي مندوزا إي ريوس في 1801.^[2]^[3] تم صياغة الاسم الإنجليزي "Haversine" في عام 1835 من قبل جيمس إنمان ^[English].^[4]^[5]

هذه الأسماء تتبع من حقيقة أنها مكتوبة عادة بدلالة دالة نصف السهم، التي ادخلها $hav(θ) = sin 2 (θ / 2)$ . ويمكن أن تكون صيغ على قدم المساواة مكتوبة بدلالة أي مضاعف نصف السهم، مثل دالة السهم القديمة. قبل ظهور الحواسيب، كان إزالة القسمة والضرب بعوامل اثنين مناسبين بما فيه الكفاية بحيث تم وضع جداول قيم نصف السهم واللوغاريتمات في النصوص عن الملاحة وحساب المثلثات في القرن التاسع عشر وأوائل القرن العشرين.^[6]^[7]^[8] في هذه الأيام، يكون شكل نصف السهم مناسبًا أيضًا لأنه لا يحتوي على معامل أمام دالة مربع الجيب $sin 2$ .

صياغة

لتكن الزاوية المركزية $Θ$ بين أي نقطتين على الكرة:

$Θ = \frac{d}{r}$

حيث:

$d$ هو المسافة بين النقطتين على طول دائرة عظمى من الكرة
$r$ هو نصف قطر الكرة

تسمح صيغة نصف السهم بحساب نصف سهم الزاوية $Θ$ (أي $hav(Θ)$ )) مباشرة من خط العرض وخط الطول للنقطتين:

h a v (Θ) = h a v (φ_{2} - φ_{1}) + \cos (φ_{1}) \cos (φ_{2}) h a v (λ_{2} - λ_{1})

حيث

$φ 1$ ، $φ 2$ هما خط عرض النقطة 1 والنقطة 2 (بالراديان)،
$λ 1$ ، $λ 2$ هي خط الطول من النقطة 1 وخط طول من النقطة 2 (في راديان).

وأخيرا، فإن دالة نصف السهم $hav(Θ)$ ، المطبقة أعلاه على كل من الزاوية المركزية $Θ$ والفروق في خط العرض وخط الطول، هي:

h a v (θ) = \sin^{2} (\frac{θ}{2}) = \frac{1 - \cos (θ)}{2}

لحل المسافة d، نقوم بتطبيق دالة «قوس نصف السهم» (الدالة العكسية لنصف السهم) على $h = hav(Θ)$ أو استخدام دالة قوس الجيب (دالة عكسية للجيب):

d = r a r c h a v (h) = 2 r \arcsin (\sqrt{h})

أو بشكل أكثر وضوحًا:^[9]

\begin{array}{r} d & = 2 r \arcsin (\sqrt{h a v (φ_{2} - φ_{1}) + (1 - h a v (φ_{1} - φ_{2}) - h a v (φ_{1} + φ_{2})) \cdot h a v (λ_{2} - λ_{1})}) \\ = 2 r \arcsin (\sqrt{\sin^{2} (\frac{φ_{2} - φ_{1}}{2}) + (1 - \sin^{2} (\frac{φ_{2} - φ_{1}}{2}) - \sin^{2} (\frac{φ_{2} + φ_{1}}{2})) \cdot \sin^{2} (\frac{λ_{2} - λ_{1}}{2})}) \\ = 2 r \arcsin (\sqrt{\sin^{2} (\frac{φ_{2} - φ_{1}}{2}) + \cos φ_{1} \cdot \cos φ_{2} \cdot \sin^{2} (\frac{λ_{2} - λ_{1}}{2})}) . \end{array}

عند استخدام هذه الصيغ، يجب على المرء التأكد من أن $h$ لا يتجاوز 1 بسبب خطأ الفاصلة المتحركة ( $d$ هو عدد حقيقي وحيد من أجل $0 \leq h \leq 1$ ). $h$ يقترب فقط من 1 للنقاط المتقابلة قطريًا (على جوانب المتقابلة للكرة) -- في هذه المنطقة، تؤول الأخطاء العددية الكبيرة نسبيًا إلى الظهور في الصيغة عند استخدام المحدودة. (تُكتب الصيغة أعلاه أحيانًا بدلالة دالة قوس الظل، ولكن هذا يعاني من مشاكل رقمية مماثلة بالقرب من $h = 1$ .)

كما هو موضح أدناه، يمكن كتابة صيغة مماثلة باستخدام جيب التمام (يسمى أحيانا قانون جيب للتمام الكروي، لا ينبغي الخلط بينه وبين قانون جيب التمام للهندسة المستوية) بدلا من نصف السهم، ولكن إذا كانت النقطتان متقاربتان (على سبيل المثال كيلومتر واحد، على الأرض) قد ينتهي بك الأمر مع $cos(d / R) = 0.99999999$ ، مما يؤدي إلى إجابة غير دقيقة. بما أن صيغة نصف السهم يستخدم الجيوب، فإنه يتجنب تلك المشكلة.

أي من الصيغتين هو فقط تقريب عند تطبيقه على الأرض، وهي ليست كرة مثالية: يتراوح «نصف قطر الأرض» $R$ من 6356.752 كم عند القطبين إلى 6378.137 كم عند خط الاستواء. والأهم من ذلك، أن نصف قطر انحناء خط شمال-جنوب على سطح الأرض أكبر بنسبة 1% عند القطبين (تساوي تقريبًا 6399.594 كم) منه عند خط الاستواء (تساوي تقريبًا 6335.439 كم) -- وبالتالي لا يمكن ضمان صحة صيغة نصف السهم وقانون جيب التمام إلى أفضل من 0.5%.^{[بحاجة لمصدر]} تعطى طرق أكثر دقة التي تراعي تفلطح الأرض من خلال صيغ فينسنتي ^[English] والصيغ الأخرى.

قانون نصف السهم

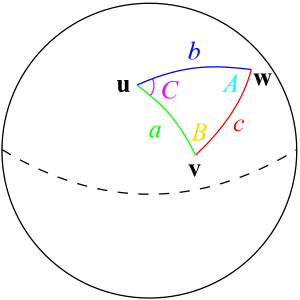
باعتبار كرة الوحدة (كرة نصف قطرها 1)، تعرَّف «المثلث» على سطح الكرة بواسطة الدوائر العظمى التي تربط ثلاث نقاط $u$ و $v$ و $w$ على الكرة. إذا كانت أطوال هذه الأضلاع الثلاثة هي $a$ (من $u$ إلى $v$ )، و $b$ (من $u$ إلى $w$ )، و $c$ (من $v$ إلى $w$ )، والزاوية المقابلة لـ $c$ هي $C$ ، فإن قانون نصف السهم ينص على ما يلي:^[10]

$h a v (c) = h a v (a - b) + \sin (a) \sin (b) h a v (C) .$

بما أن الكرة عبارة عن كرة الوحدة، فإن الأطوال $a$ و $b$ و $c$ تساوي ببساطة الزوايا (بالتقدير الدائري) التي تقابلها تلك الجوانب من مركز الكرة (بالنسبة إلى كرة غير الوحدة، يكون كل من تلك أطوال الأقواس مساويًا لزاويتها المركزية مضروبًا في نصف القطر $R$ للكرة).

من أجل الحصول على صيغة نصف السهم للقسم السابق من هذا القانون، نعتبر ببساطة الحالة الخاصة حيث u هو القطب الشمالي، بينما $v$ و $w$ هما النقطتان اللتان ستحدَّد فصلهما $d$ . في هذه الحالة، $a$ و $b$ هن $π / 2 - φ 1,2$ (أي، تمام العرض)، و $"c"$ هو فصل خط الطول $d / R$ ، و $"c"$ هو $λ 2 - λ 1$ المطلوب. مشيرا إلى أن $sin(π / 2 - φ) = cos(φ)$ ، يتبع صيغة نصف السهم على الفور.

لاشتقاق قانون نصف السهم، نبدأ مع قانون جيب التمام الكروي:

$\cos (c) = \cos (a) \cos (b) + \sin (a) \sin (b) \cos (C) .$

كما ذكرنا أعلاه، فإن هذه الصيغة هي طريقة غير مشروطة لحل $"c"$ عندما تكون $"c"$ صغيرة. بدلاً من ذلك، نعوض المتطابقة $cos(θ) = 1 - 2 hav(θ)$ ، ونستخدم أيضاً متطابقة الفرق $cos(a - b) = cos(a) cos(b) + sin(a) sin(b)$ ، للحصول على قانون نصف السهم المذكور الأعلاه.

انظر أيضًا

مسافة دائرة عظمى

ملاحظات ومراجع

ملاحظات

^ ^أ ^ب المصطلح الإنجليزي Haversine هو الاختصار لعبارة Half a versed sine التي تعني نصف الجيب المعكوس أو نصف السهم، حيث الجيب المعكوس أو السهم هو دالة مثلثية تمثل الفرق بين جيب تمام زاوية محددة والواحد، التسميتان العربيتان مذكورتان في عدة كتب قديمة منها القانون المسعودي للعالم البيروني وكشاف اصطلاحات الفنون للتهانوي

مراجع

^ van Brummelen، Glen Robert (2013). Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry. دار نشر جامعة برنستون. ISBN:9780691148922. 0691148929. مؤرشف من الأصل في 2020-07-23. اطلع عليه بتاريخ 2015-11-10.
^ de Mendoza y Ríos, Joseph (1795). Memoria sobre algunos métodos nuevos de calcular la longitud por las distancias lunares: y aplicacion de su teórica á la solucion de otros problemas de navegacion (بالإسبانية). Madrid, Spain: Imprenta Real. Archived from the original on 2020-06-11.
^ Cajori، Florian (1952) [1929]. A History of Mathematical Notations (ط. 2 (3rd corrected printing of 1929 issue)). Chicago: Open court publishing company. ج. 2. ص. 172. ISBN:978-1-60206-714-1. 1602067147. مؤرشف من الأصل في 2020-07-17. اطلع عليه بتاريخ 2015-11-11. The haversine first appears in the tables of logarithmic versines of جوسيف دي مندوزا إي ريوس (Madrid, 1801, also 1805, 1809), and later in a treatise on navigation of James Inman (1821). (NB. ISBN and link for reprint of second edition by Cosimo, Inc., New York, 2013.)
^ Inman، James (1835) [1821]. Navigation and Nautical Astronomy: For the Use of British Seamen (ط. 3). London, UK: W. Woodward, C. & J. Rivington. مؤرشف من الأصل في 2020-06-11. اطلع عليه بتاريخ 2015-11-09. (Fourth edition: [1].)
^ قالب:OED2
^ H. B. Goodwin, The haversine in nautical astronomy, Naval Institute Proceedings, vol. 36, no. 3 (1910), pp. 735–746: Evidently if a Table of Haversines is employed we shall be saved in the first instance the trouble of dividing the sum of the logarithms by two, and in the second place of multiplying the angle taken from the tables by the same number. This is the special advantage of the form of table first introduced by Professor Inman, of the Portsmouth Royal Navy College, nearly a century ago. نسخة محفوظة 2020-05-10 على موقع واي باك مشين.
^ W. W. Sheppard and C. C. Soule, Practical navigation (World Technical Institute: Jersey City, 1922). نسخة محفوظة 2020-07-23 على موقع واي باك مشين.
^ E. R. Hedrick, Logarithmic and Trigonometric Tables (Macmillan, New York, 1913).
^ Gade، Kenneth (2010). "A Non-singular Horizontal Position Representation". Journal of Navigation. ج. 63 ع. 3: 395–417. DOI:10.1017/S0373463309990415. ISSN:0373-4633.
^ Korn، Grandino Arthur؛ Korn، Theresa M. (2000) [1922]. "Appendix B: B9. Plane and Spherical Trigonometry: Formulas Expressed in Terms of the Haversine Function". Mathematical handbook for scientists and engineers: Definitions, theorems, and formulas for reference and review (ط. 3rd). Mineola, New York: Dover Publications. ص. 892–893. ISBN:978-0-486-41147-7. مؤرشف من الأصل في 2022-06-11.

قراءة متعمقة

U. S. Census Bureau Geographic Information Systems FAQ, (content has been moved to What is the best way to calculate the distance between 2 points?)
R. W. Sinnott, "Virtues of the Haversine", Sky and Telescope 68 (2), 159 (1984).
Deriving the haversine formula, Ask Dr. Math (Apr. 20–21, 1999).
Romuald Ireneus 'Scibor-Marchocki, Spherical trigonometry, Elementary-Geometry Trigonometry web page (1997).
W. Gellert, S. Gottwald, M. Hellwich, H. Kästner, and H. Küstner, The VNR Concise Encyclopedia of Mathematics, 2nd ed., ch. 12 (Van Nostrand Reinhold: New York, 1989).

روابط خارجية

Implementations of the haversine formula in 91 languages at rosettacode.org and in 17 languages on codecodex.com
Other implementations in C++, C (MacOS), Pascal, Python, Ruby, JavaScript, PHP,Matlab, MySQL

[ملاحظة_1-1] أ ^ب المصطلح الإنجليزي Haversine هو الاختصار لعبارة Half a versed sine التي تعني نصف الجيب المعكوس أو نصف السهم، حيث الجيب المعكوس أو السهم هو دالة مثلثية تمثل الفرق بين جيب تمام زاوية محددة والواحد، التسميتان العربيتان مذكورتان في عدة كتب قديمة منها القانون المسعودي للعالم البيروني وكشاف اصطلاحات الفنون للتهانوي

[Brummelen_2013-2] van Brummelen، Glen Robert (2013). Heavenly Mathematics: The Forgotten Art of Spherical Trigonometry. دار نشر جامعة برنستون. ISBN:9780691148922. 0691148929. مؤرشف من الأصل في 2020-07-23. اطلع عليه بتاريخ 2015-11-10.

[Ríos_1795-3] Mendoza y Ríos, Joseph (1795). Memoria sobre algunos métodos nuevos de calcular la longitud por las distancias lunares: y aplicacion de su teórica á la solucion de otros problemas de navegacion (بالإسبانية). Madrid, Spain: Imprenta Real. Archived from the original on 2020-06-11.

[Cajori_1929-4] Cajori، Florian (1952) [1929]. A History of Mathematical Notations (ط. 2 (3rd corrected printing of 1929 issue)). Chicago: Open court publishing company. ج. 2. ص. 172. ISBN:978-1-60206-714-1. 1602067147. مؤرشف من الأصل في 2020-07-17. اطلع عليه بتاريخ 2015-11-11. The haversine first appears in the tables of logarithmic versines of جوسيف دي مندوزا إي ريوس (Madrid, 1801, also 1805, 1809), and later in a treatise on navigation of James Inman (1821). (NB. ISBN and link for reprint of second edition by Cosimo, Inc., New York, 2013.)

[Inman_1835-5] Inman، James (1835) [1821]. Navigation and Nautical Astronomy: For the Use of British Seamen (ط. 3). London, UK: W. Woodward, C. & J. Rivington. مؤرشف من الأصل في 2020-06-11. اطلع عليه بتاريخ 2015-11-09. (Fourth edition: [1].)

[OED_1989_Haversine-6] قالب:OED2

[7] H. B. Goodwin, The haversine in nautical astronomy, Naval Institute Proceedings, vol. 36, no. 3 (1910), pp. 735–746: Evidently if a Table of Haversines is employed we shall be saved in the first instance the trouble of dividing the sum of the logarithms by two, and in the second place of multiplying the angle taken from the tables by the same number. This is the special advantage of the form of table first introduced by Professor Inman, of the Portsmouth Royal Navy College, nearly a century ago. نسخة محفوظة 2020-05-10 على موقع واي باك مشين.

[8] W. W. Sheppard and C. C. Soule, Practical navigation (World Technical Institute: Jersey City, 1922). نسخة محفوظة 2020-07-23 على موقع واي باك مشين.

[9] E. R. Hedrick, Logarithmic and Trigonometric Tables (Macmillan, New York, 1913).

[Gade2010-10] Gade، Kenneth (2010). "A Non-singular Horizontal Position Representation". Journal of Navigation. ج. 63 ع. 3: 395–417. DOI:10.1017/S0373463309990415. ISSN:0373-4633.

[Korn_2000-11] Korn، Grandino Arthur؛ Korn، Theresa M. (2000) [1922]. "Appendix B: B9. Plane and Spherical Trigonometry: Formulas Expressed in Terms of the Haversine Function". Mathematical handbook for scientists and engineers: Definitions, theorems, and formulas for reference and review (ط. 3rd). Mineola, New York: Dover Publications. ص. 892–893. ISBN:978-0-486-41147-7. مؤرشف من الأصل في 2022-06-11.

[ملاحظة 1]

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

بحاجة لمصدر

[10]

صيغة نصف السهم

محتويات

صياغة

قانون نصف السهم

انظر أيضًا

ملاحظات ومراجع

ملاحظات

مراجع

قراءة متعمقة

روابط خارجية

قائمة التصفح

صيغة نصف السهم

صياغة

قانون نصف السهم

انظر أيضًا

ملاحظات ومراجع

ملاحظات

مراجع

قراءة متعمقة

روابط خارجية

قائمة التصفح

بحث