قوس (هندسة)

  لمعانٍ أخرى، طالع قوس (توضيح).

قوس طوله $L$ في دائرة نصف قطرها $r$ محدد بقطاع دائري (بالأخضر) زاويته $\theta$

في الهندسة الإقليدية، القوس هو قطعة من منحني قابل للاشتقاق في المستوي. على سبيل المثال قوس من دائرة هو قطعة من محيط الدائرة.

قوس الدائرة

القوس الأصغر: هو القوس الأقصر طولاً الذي يكون محصوراً بين نصفي قطرين من الدائرة ويساوي طول الزاوية المركزية التي يحصرها ولا يزيد عن $180^{\circ }$.
القوس الأكبر: هو القوس الأكثر طولاً ويكون محصوراً بين نصفي قطرين من الدائرة ويساوي طول الزاوية المركزيَة التي يحصرها ويكون طوله يزيد عن $180^{\circ }$ و يقل عن $360^{\circ }$
قوس نصف الدائرة: هو القوس الذي تكون نقطتاه النهائيتان على طرفي قطر الدائرة ويكون طوله يساوي $180^{\circ }$.

القوس الأكبر والقوس الأصغر	قوس نصف الدائرة
لا إطار

قياس القوس

المقالات الرئيسية: درجة (زاوية) وراديان

يُعبِّرُ مصطلحُ «قياس القوس» إلى قياسِ الزاويةِ المركزيةِ التي تَحصِرُ القوسَ. وباعتبار أن الدائرة قوساً مُتَّصِلَ الطَّرفَينِ فإن قياسُها بالدرجاتِ

$360^{\circ }$

. وعلى ذلكَ، فإن قياسَ الأقواسِ الناتجةِ عنْ قَطْعِ زاويةٍ مركزيةٍ لدائرتينِ متحدتَيْ المركزِ لهُمَا القياسَ نَفْسَهُ؛ لاشتراكِهِما في قياسِ الزاويةِ المركزيةِ. ويتطابقُ قوسانِ من دائرةٍ واحدةٍ إذا وفقط إذا كان لهُما القياسَ نَفسه. وهُناكَ قياسانِ شهيرانِ للقوسِ:

الدرجة	الراديان
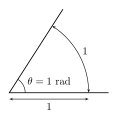
يُعرَّف القوس الذي قياسه درجة واحدة على أنه $\frac{1}{360}$من قياس الدائرة كاملةً.	يُعرَّف القوس الذي قياسه راديان واحد على أنه القوس الذي طوله نصف قطر الدائرة الأصلية $r$.

النقطتان $A,B$تقسمان الدائرة إلى قوسين: قوس أكبر، وقوس أصغر.

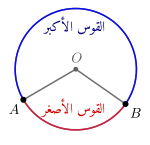
إذا كانت

$A,B$

نقطتين مختلفتين على الدائرة

$C(O,r)$

فإنهما يقسمان الدائرة إلى قوسين: قوس أصغر

$\widehat{AB}$

، وقوس أكبر

$\widehat{AB}$

يتممان بعضهما بعضاً. يُرمَز إلى القوس الأكبر

$\widehat{AB}$

أحياناً بالرمز

$\widehat{ACB}$

عِوَضاً عن ذكر «

$\widehat{AB}$

الأكبر». يُعرّف القوس الأصغر

$\widehat{AB}$

على أنَّه مجموعةُ النّقاط الناتجةِ عن تقاطعِ الدائرةِ مع نقاطِ الزاويةِ المركزية

$\mathrm{\angle }AOB$

الداخلية ويُعبَّرُ عنه أيضاً بأنه القوس الأقصر طولاً الذي يصل بين النقطتين

$A,B$

على الدَّائرة، حيثُ يُساوي قياسه قياسَ الزَّاويةِ المركزيةِ المُقابلةِ لَهُ، ويقل عن

$180^{\circ }$

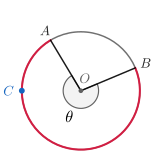
. على الوجه المقابل، فإن القوس الأكبر

$\widehat{AB}$

هو مجموعةُ النّقاط الناتجةِ عن تقاطعِ الدائرةِ مع نقاطِ الزاويةِ المركزية

$\mathrm{\angle }AOB$

المُنعكِسة ويُعبَّرُ عنه أيضاً بأنه القوس الأقصر طولاً الذي يصل بين النقطتين

$A,B$

على الدَّائرة، حيثُ يُساوي قياسه قياسَ الزَّاويةِ المركزيةِ المُقابلةِ لَهُ، ويزيد عن

$180^{\circ }$

. تُسمَّى النقطتان

$A,B$

طرفا القوس

$\widehat{AB}$

أو طرفا الوتر

$\overline{AB}$

. في حالِ كَوْنِ النُّقطتينِ

$A,B$

نقطتينِ متقابلتينِ قُطريَّاً، فإن كُلاً مِن القَوسَيْنِ المُقَابِلَيْنِ لَهُمَا القياس نفسه، ويُسمَّى القوسُ الواحدُ نِصفَ دَائرةٍ. وكُلُّ قِطْرٍ في دائرةٍ ما يُحدِّدُ نِصفَيْ دائرةٍ.

إذا كانَ طُولُ القوْسِ يُساوي $\ell$، فإنَّ النسبةَ بينَ طولِ القوسِ إلى مُحيطِ الدَّائرةِ يُساوي نسبةَ قياسِ القوسِ إلى قِياسِ الدَّائرةِ كاملةً.

$$\frac{l}{C_O}=\frac{l}{2\pi r}=\frac{{\theta }^{\circ }}{360^{\circ }}\iff \ell =\pi r\cdot \frac{{\theta }^{\circ }}{180^{\circ }}$$

القوس الأصغر $\widehat{AB}$	القوس الأكبر $\widehat{AB}$ (أو اختصاراً $\widehat{ACB}$)	نصف الدَّائرة $\widehat{ADB}$

صيغ رياضية

إذا كان طول القوس يساوي $\ell$، فإنَّ النسبة بين طول القوس إلى مُحيط الدَّائرة يُساوي نسبة قياس القوس إلى قياس الدَّائرة كاملةً.

$\frac{l}{C_O}=\frac{l}{2\pi r}=\frac{{\theta }^{\circ }}{360^{\circ }}\iff \ell =\pi r\cdot \frac{{\theta }^{\circ }}{180^{\circ }}$

انظر أيضاً

• طول قوس
• زاوية مركزية
• قطاع دائري
• جزء دائري
• قوس (عمارة)