|
تضامنًا مع حق الشعب الفلسطيني |
توزيع بواسون
دالة الكثافة الاحتمالية 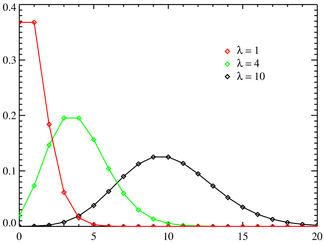
| |
دالة التوزيع التراكمي 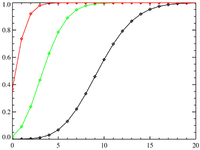 | |
| المؤشرات | |
| الدعم | |
| د۔ك۔ح۔ | |
| د۔ت۔ت | |
| المتوسط الحسابي | |
| الوسيط الحسابي | |
| المنوال | |
| التباين | |
| التجانف | |
| التفرطح | |
| الاعتلاج | |
| د۔م۔ع | |
| الدالة المميزة | |
| معلومات فيشر | {{{معلومات فيشر}}} |
توزيع بواسون (بالإنجليزية: Poisson distribution)(/ˈpwɑːsɒn/; تنطق بالفرنسية: [pwasɔ̃] )،(ويسمى أيضا قانون بواسون للأعداد الصغيرة[1]) هو توزيع احتمالي منفصل يعبر عن احتمالية حدوث عدد من الأحداث ضمن فترة محددة من الوقت إذا حدثت هذه الأحداث بمعدل وسطي معروف وغير متعلقة بزمن حدوث آخر حدث.
في نظرية الاحتمالات والإحصاءات هو التوزيع الاحتمالي المنفصل الذي سمي على اسم عالم الرياضيات الفرنسي سيميون دينيس بواسون، وهو توزيع احتمالي منفصل يعبر عن احتمال حدوث عدد معين من الأحداث في الفاصل الزمني أو المكان إذا حدثت هذه الأحداث بمعدل متوسط ثابت معروف وبشكل مستقل عن الزمن منذ آخر حدث. يمكن أيضًا استخدام توزيع بواسون لعدد الأحداث في فترات زمنية محددة أخرى مثل المسافة أو المنطقة أو الحجم.
على سبيل المثال، يتلقى مركز الاتصال الهاتفي 180 مكالمة في المتوسط في الساعة، 24 ساعة في اليوم. المكالمات مستقلة. استقبال واحد لا يغير من احتمالية وصول الآخر. عدد المكالمات التي يتم تلقيها خلال أي دقيقة له توزيع احتمالية بواسون: الرقم الأكثر احتمالًا هو 3، ولكن من المحتمل أيضًا أن يكون الرقم 2 أو 4 محتملًا؛ وهناك احتمال ضئيل لكونه منخفضًا حتى الصفر وكذلك احتمال صغير جدًا أن يكون 10 .
مثال آخر هو عدد أحداث الانحلال التي تحدث من مصدر مشع في فترة مراقبة معينة قصيرة.
في مدّة زمنية T، يحصل الحدث بمعدل λ مرّات (λ أقل من 5 مثلا). لنرمز ب X المتغير العشوائي الذي يمثل عدد المرّات التي سيحصل فيها الحدث في X. T يمكن أن يساوي 0، 1، 2...
يتبع هذا المتغير العشوائي القانون التالي:
مهما كان العدد الطبيعي k.
- λعدد حقيقي موجب
- (p(k : احتمال حصول الحدث k في T.
هذا ما يدعى توزيع بواسون (أو قانون بواسون) ذا المعلمة λ.
تعريفات
دالة الكتلة الاحتمالية
يعتبر توزيع بواسون شائعًا لنمذجة عدد المرات التي يقع فيها الحدث في فترة زمنية أو مساحة .
يُقال إن المتغير العشوائي X المنفصل له توزيع بواسون مع المعامل المتغير λ> 0 إذا كان لـ k = 0، 1، 2... دالة الكتلة الاحتمالية لـ X تعطى بواسطة:[2]
عندما
الرقم الحقيقي الموجب λ يساوي القيمة المتوقعة لـ X وأيضًا تباينها [3]
يمكن تطبيق توزيع بواسون على الأنظمة التي بها عدد كبير من الأحداث المحتملة، كل منها نادر الحدوث. عدد مثل هذه الأحداث التي تحدث خلال فترة زمنية محددة، في ظل الظروف المناسبة، هو رقم عشوائي مع توزيع بواسون.
يمكن تكييف المعادلة إذا، بدلاً من متوسط عدد الأحداث ، نحصل على معدل زمني لعدد الأحداث يحدث. ثم (عرض عدد الأحداث لكل وحدة زمنية)، و
مثال
قد يكون توزيع بواسون مفيدًا لنمذجة أحداث مثل
- عدد النيازك التي يزيد قطرها عن متر واحد والتي تضرب الأرض في السنة.
- عدد المرضى الذين يصلون إلى غرفة الطوارئ بين الساعة 10 و 11 مساءً.
- عدد فوتونات الليزر التي تصطدم بالكاشف في فترة زمنية معينة.
الافتراضات والصلاحية
يعتبر توزيع بواسون نموذجًا مناسبًا إذا كانت الافتراضات التالية صحيحة: [4]
- k هو عدد المرات التي يقع فيها حدث ما في فترة ما ويمكن لـ k أن تأخذ القيم 0، 1، 2....
- لا يؤثر وقوع حدث واحد على احتمال وقوع حدث ثان. أي أن الأحداث تحدث بشكل مستقل.
- متوسط المعدل الذي تحدث به الأحداث مستقل عن أي تكرارات. من أجل التبسيط، يُفترض عادةً أن يكون هذا ثابتًا، ولكن قد يختلف عمليًا مع مرور الوقت.
- لا يمكن أن يحدث حدثان في نفس اللحظة بالضبط؛ بدلاً من ذلك، في كل فترة فرعية صغيرة جدًا، يحدث حدث واحد بالضبط أو لا يحدث.
إذا كانت هذه الشروط صحيحة، فإن k هو متغير بواسون العشوائي، وتوزيع k هو توزيع بواسون.
توزيع بواسون هو أيضًا حد التوزيع ذي الحدين، حيث يساوي احتمال النجاح لكل تجربة λ مقسومًا على عدد التجارب، حيث يقترب عدد التجارب من اللانهاية (انظر التوزيعات ذات الصلة).
أمثلة على احتمالية توزيعات بواسون
|
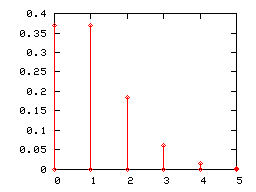
في نهر معين، تحدث فيضانات الفائض مرة كل 100 عام في المتوسط. احسب احتمالk= 0، 1، 2، 3، 4، 5، أو 6 فيضان فيضان في فترة 100 سنة، على افتراض أن نموذج بواسون مناسب. لأن متوسط معدل الحدث هو فيضان فائض واحد لكل 100 عام، λ = 1 |
يعطي الجدول أدناه احتمالية حدوث 0 إلى 6 فيضانات في فترة 100 عام.
|
|
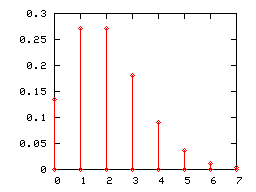
أفاد أوغارتي وزملاؤه أن متوسط عدد الأهداف في إحدى مباريات كأس العالم لكرة القدم يبلغ 2.5 تقريبًا وأن نموذج بواسون مناسب. [5] لأن متوسط معدل الحدث 2.5 هدف لكل مباراة، λ = 2.5. |
يعطي الجدول أدناه الاحتمال من 0 إلى 7 أهداف في المباراة.
|
مرة واحدة في الأحداث الفاصلة: حالة خاصة من λ = 1 و k = 0
لنفترض أن الفلكيين يقدرون أن النيازك الكبيرة (فوق حجم معين) ضربت الأرض في المتوسط مرة كل 100 سنة (λ = 1 حالة لكل 100 سنة)، وأن عدد الزيارات النيزك يتبع توزيع بواسون. ما هو احتمال k = 0 يضرب نيزك في المائة عام القادمة؟
في ظل هذه الافتراضات، فإن احتمال عدم اصطدام أي نيازك كبيرة بالأرض خلال المائة عام القادمة هو 0.37 تقريبًا. الباقي 1 - 0.37 = 0.63 هو احتمال حدوث 1، 2، 3، أو أكثر من ضربات نيزك كبير في المائة عام القادمة. في المثال أعلاه، حدث فيضان فائض مرة كل 100 عام (λ = 1). كان احتمال عدم حدوث فيضانات فائضة خلال 100 عام تقريبًا 0.37، بنفس الحساب.
بشكل عام، إذا حدث حدث ما في المتوسط مرة واحدة لكل فترة زمنية (λ = 1)، وتتبع الأحداث توزيع بواسون، ثم P (0 أحداث في الفترة التالية) & nbsp ؛ = 0.37. بالإضافة إلى ذلك، P (حدث واحد بالضبط في الفترة التالية) = 0.37، كما هو موضح في الجدول لفيضانات الفائض.
أمثلة تنتهك افتراضات بواسون
من المحتمل ألا يتبع عدد الطلاب الذين يصلون إلى اتحاد الطلاب في الدقيقة توزيع بواسون، لأن المعدل ليس ثابتًا (معدل منخفض أثناء وقت الفصل، ومعدل مرتفع بين أوقات الفصل) وقادمات الطلاب الفرديين ليسوا مستقلين (الطلاب تميل إلى المجيء في مجموعات).
قد لا يتبع عدد الزلازل التي تبلغ قوتها 5 درجات سنويًا في بلد ما توزيع بواسون إذا زاد زلزال واحد كبير من احتمال حدوث توابع من نفس الحجم.
الأمثلة التي يتم فيها ضمان حدث واحد على الأقل لا يتم توزيع بواسون؛ ولكن يمكن نمذجتها باستخدام توزيع بواسون بدون اقتطاع.
يمكن نمذجة توزيعات العد التي يكون فيها عدد الفترات ذات الأحداث الصفرية أعلى من المتوقع بواسطة نموذج بواسون باستخدام نموذج مضخم صفري.
تميز
الإحصاء الوصفي
- تساوي القيمة والتباين المتوقعان لمتغير عشوائي موزع بواسون λ.
- معامل الاختلاف هو بينما مؤشر التشتت 1. [6]
- متوسط الانحراف المطلق عن المتوسط هو [6]
- وضع المتغير العشوائي الموزع بواسون مع عدد غير صحيح يساوي ، وهو أكبر عدد صحيح أصغر من أو يساوي λ . هذا هو مكتوب أيضا الكلمة (λ). عندما λ هو عدد صحيح موجب، وسائط هي λ λ و - 1.
- جميع تراكمات توزيع بواسون تساوي القيمة المتوقعة λ . العزم المضروب n لتوزيع بواسون هو λ n .
- تتحلل أحيانًا القيمة المتوقعة لعملية بواسون إلى نتاج الكثافة والتعرض (أو يتم التعبير عنها عمومًا على أنها جزء لا يتجزأ من «وظيفة الكثافة» عبر الزمان أو المكان، والتي توصف أحيانًا باسم «التعرض»). [7]
الوسيط

حدود الوسيط () من التوزيع معروف وحاد: [8]
لحظات أعلى
اللحظات الأعلى حول الأصل، m · k لتوزيع بواسون، هي توشارد كثيرات الحدود في λ:
- حيث تشير {الأقواس} إلى أرقام ستيرلنغ من النوع الثاني. [9] [10] معاملات كثيرات الحدود لها معنى اندماجي. في الواقع، عندما تكون القيمة المتوقعة لتوزيع بواسون هي 1، فإن صيغة دوبينسكي تقول إن اللحظة n تساوي عدد الأقسام لمجموعة من الحجم n .
للحظات غير المركزية نحددها ، ثم [11]
عندما هو الثابت المطلق أكبر من 0.
مجموع المتغيرات العشوائية الموزعة بواسون
- لو بالنسبة مستقلة، إذن . [12] العكس هو نظرية رايكوف، التي تقول أنه إذا كان مجموع متغيرين عشوائيين مستقلين موزعًا بواسون، فسيكون كذلك كل من هذين المتغيرين العشوائيين المستقلين. [13] [14]
خصائص أخرى
- توزيعات بواسون هي توزيعات احتمالية لا نهائية للقسمة. [15] [6]
- الاختلاف الموجه تباعد كولباك - ليبلير من اعطي من قبل
- يمكن اشتقاقها باستخدام وسيطة منضمة لـ تشيرنوف. [16]
- و
- يمكن تشديد احتمال الذيل العلوي (بمعامل لا يقل عن اثنين) على النحو التالي: [17]
أين هو التباعد الموجه كولباك – ليبلر، كما هو موضح أعلاه.
المتباينات التي تربط دالة التوزيع لمتغير بواسون العشوائي إلى دالة التوزيع العادي القياسية هي كالتالي: [17]
أين هو مرة أخرى اختلاف كولباك – ليبلر الموجه.
سباقات بواسون
يترك و تكون متغيرات عشوائية مستقلة، مع ، ثم لدينا ذلك
تم إثبات الحد الأعلى باستخدام حد تشيرنوف القياسي.
يمكن إثبات الحد الأدنى بملاحظة ذلك هو احتمال أن ، أين ، والتي يحدها أدناه ، أين هو إنتروبيا نسبية (انظر المدخل على حدود ذيول التوزيعات ذات الحدين لمزيد من التفاصيل). كذلك مشيرا إلى أن ، وحساب الحد الأدنى على الاحتمال غير المشروط يعطي النتيجة. يمكن العثور على مزيد من التفاصيل في ملحق كاماث وآخرون. [18]
التوزيعات ذات الصلة
عام
- لو و مستقلة، ثم الاختلاف يتبع توزيع سكيلام.
- لو و مستقلة، ثم توزيع على الشرطي هو توزيع ذو الحدين.
- على وجه التحديد، إذا ، من ثم .
- بشكل عام، إذا كانت X 1، X 2. . . X n هي متغيرات بواسون العشوائية المستقلة مع المعلمات λ 1، λ 2... λ n ثم
- معطى . في الحقيقة،
- لو وتوزيع ، شرطي على X = ك، هو توزيع ذي الحدين، ، ثم يتبع توزيع Y توزيع بواسون . في الواقع، إذا ، الشرطي على X = k، يتبع توزيعًا متعدد الحدود، ، ثم كل منهما يتبع توزيع بواسون المستقل .
- يمكن اشتقاق توزيع بواسون كحالة مقيدة للتوزيع ذي الحدين حيث أن عدد المحاكمات يذهب إلى اللانهاية والعدد المتوقع للنجاحات يظل ثابتًا - انظر قانون الأحداث النادرة أدناه. لذلك، يمكن استخدامه كتقريب للتوزيع ذي الحدين إذا كان n كبيرًا بدرجة كافية وكان p صغيرًا بدرجة كافية. هناك قاعدة عامة تنص على أن توزيع بواسون هو تقريب جيد للتوزيع ذي الحدين إذا كان n على الأقل 20 و p أصغر من أو يساوي 0.05، وتقريب ممتاز إذا كان n ≥ 100 و np ≤ 10- [19]
- توزيع بواسون هو حالة خاصة لتوزيع بواسون المركب المنفصل (أو توزيع بواسون المتلعثم) بمعامل فقط. [20][21] يمكن استنتاج توزيع بواسون المركب المنفصل من التوزيع المحدود للتوزيع أحادي المتغير متعدد الحدود. وهي أيضًا حالة خاصة لتوزيع بواسون المركب.
- للحصول على قيم كبيرة بما فيه الكفاية لـ λ، (مثل λ> 1000)، التوزيع الطبيعي بمتوسط λ والتباين λ (الانحراف المعياري ) هو تقريب ممتاز لتوزيع بواسون. إذا كانت أكبر من حوالي 10، فإن التوزيع الطبيعي هو تقريب جيد إذا تم إجراء تصحيح استمراري مناسب، أي إذا كان P (X ≤ x)، حيث x هو عدد صحيح غير سالب، يتم استبداله بـ P (X ≤ x + 0.5).
- تحول استقرار التباين: إذا ، من ثم
- ، [6]
- و
- . [22]
- في ظل هذا التحول، التقارب إلى الحالة الطبيعية (مثل الزيادات) أسرع بكثير من المتغير غير المحول. تحويلات أخرى، أكثر تعقيدًا قليلاً، لتثبيت التباين متاحة، [6] أحدها هو تحويل أنسكومب. [23] انظر تحويل البيانات (الإحصائيات) لمزيد من الاستخدامات العامة للتحولات.
- إذا كان لكل ر > 0 عدد الوافدين في الفترة الزمنية [0، t ] يتبع توزيع بواسون بمتوسط λt، ثم يكون تسلسل أوقات الوصول بين المتغيرات المستقلة والأسية الموزعة بشكل متماثل لها متوسط 1 / λ . [24]
- ترتبط دالات التوزيع التراكمي لتوزيعات بواسون وكي تربيع بالطرق التالية: [6]
و
تقريب بواسون
افترض أين ، ثم [25] يتم توزيعها بشكل متعدد الحدود مشروط .
هذا يعني [16]، من بين أمور أخرى، ذلك لأي وظيفة غير سلبية ، لو يتم توزيعها متعدد الحدود، إذن
عندما .
عامل يمكن استبداله بـ 2 إذا يُفترض أيضًا أنه يتزايد أو يتناقص بشكل رتيب.
توزيع بواسون ثنائي المتغير
تم تمديد هذا التوزيع إلى حالة ثنائية المتغير. [26] وظيفة التوليد لهذا التوزيع هي
مع
التوزيعات الهامشية هي بواسون (θ 1) وبواسون (θ 2) ومعامل الارتباط يقتصر على مجموعة
طريقة بسيطة لتوليد توزيع بواسون ثنائي المتغير هو أخذ ثلاث توزيعات بواسون مستقلة بالوسائل ثم ضبط . دالة الاحتمال لتوزيع بواسون ثنائي المتغير هي
توزيع بواسون مجاني
توزيع بواسون المجاني [27] بحجم قفزة ومعدل ينشأ في نظرية الاحتمالات الحرة كحد أقصى للالتفاف الحر المتكرر
مثل N. → ∞.
وبعبارة أخرى، دعونا تكون متغيرات عشوائية بحيث له قيمة مع الاحتمال والقيمة 0 مع الاحتمال المتبقي. افترض أيضا أن الأسرة مستقلة بحرية. ثم الحد كما من قانون يتم تقديمها بموجب قانون بواسون الحر مع المعلمات .
هذا التعريف مشابه لإحدى الطرق التي يتم بها الحصول على توزيع بواسون الكلاسيكي من عملية بواسون (كلاسيكية).
يتم إعطاء التدبير المرتبط بقانون بواسون المجاني بواسطة [28]
عندما
ولديه دعم .
ينشأ هذا القانون أيضًا في نظرية المصفوفة العشوائية مثل قانون مارشينكو - باستور. المتراكمات الحرة لها تساوي .
بعض التحولات في هذا القانون
نعطي قيمًا لبعض التحولات المهمة لقانون بواسون الحر؛ يمكن العثور على الحساب في، على سبيل المثال، في كتاب «محاضرتان حول توافقيات الاحتمالية الحرة بواسطة أ. نيكا ور. سبايشر».[29]
يتم إعطاء تحويل R لقانون بواسون المجاني بواسطة
يتم إعطاء تحويل كوشي (وهو سلبي لتحويل ستيلجس) بواسطة
يتم إعطاء تحويل S بواسطة
في الحالة تلك .
الاستدلال الإحصائي
تقدير المعامل المتغير
إعطاء عينة من القيم المقاسة n ، لأني = 1، ... ن، نرغب في تقدير قيمة المعلمة λ لمجتمع بواسون الذي تم سحب العينة منه. تقدير الاحتمالية القصوى هو [30]
نظرًا لأن كل ملاحظة لها توقع λ فهل تعني العينة. لذلك، فإن تقدير الاحتمالية القصوى هو مقدر غير متحيز لـ λ. وهو أيضًا مقدر فعال نظرًا لأن تباينه يحقق الحد الأدنى كرامر - راو (CRLB). ومن ثم فإن التباين الأدنى غير متحيز. كما يمكن إثبات أن المجموع (ومن ثم متوسط العينة لأنه دالة فردية للمبلغ) هو إحصائية كاملة وكافية لـ λ.
لإثبات الكفاية، قد نستخدم نظرية العوامل. ضع في اعتبارك تقسيم دالة الكتلة الاحتمالية لتوزيع بواسون المشترك للعينة إلى جزأين: جزء يعتمد فقط على العينة (مسمى ) وواحد يعتمد على المعلمة والعينة فقط من خلال الوظيفة . ثم إحصائية كافية لـ .
الفصل الأول، ، يعتمد فقط على . الفصل الثاني، ، يعتمد على العينة فقط من خلال . هكذا، كافي.
للعثور على المعلمة λ التي تزيد من دالة الاحتمال لسكان بواسون، يمكننا استخدام لوغاريتم دالة الاحتمال:
نأخذ مشتق من فيما يتعلق λ وذلك لمقارنة الصفر:
الحل من أجل λ يعطي نقطة ثابتة.
إذن λ هو متوسط قيم k i . الحصول على علامة المشتق الثاني لـ L عند النقطة الثابتة سيحدد نوع القيمة القصوى λ .
يعطي تقييم المشتق الثاني عند النقطة الثابتة :
وهو سالب n في مقلوب متوسط k i . هذا التعبير سالب عندما يكون المتوسط موجبًا. إذا تم استيفاء ذلك، فإن النقطة الثابتة تزيد من دالة الاحتمال.
من أجل الاكتمال، يُقال أن عائلة التوزيعات كاملة إذا وفقط إذا يعني ذلك للجميع . إذا كان الفرد هي iid ، من ثم . من خلال معرفة التوزيع الذي نريد التحقيق فيه، من السهل أن نرى اكتمال الإحصاء.
من أجل هذه المساواة، يجب أن يكون 0. هذا يأتي من حقيقة أنه لن يكون أي من المصطلحات الأخرى صفرًا للجميع في المجموع ولجميع القيم الممكنة لـ . لذلك، للجميع يعني ذلك ، وقد ثبت أن الإحصاء مكتمل.
فاصل الثقة
يمكن التعبير عن فاصل الثقة لمتوسط توزيع بواسون باستخدام العلاقة بين وظائف التوزيع التراكمي لتوزيعات بواسون وكي تربيع. يرتبط توزيع مربع كاي ارتباطًا وثيقًا بتوزيع جاما، وهذا يؤدي إلى تعبير بديل. بالنظر إلى الملاحظة k من توزيع بواسون بمتوسط μ، فإن فاصل الثقة لـ μ بمستوى الثقة 1 – α هو
أو مكافئ،
أين هي الدالة الكمية (المقابلة لمنطقة الذيل السفلية p) لتوزيع مربع كاي مع n من درجات الحرية و هي دالة كميّة لتوزيع جاما بمعامل الشكل n ومعلمة المقياس 1. [6][31] هذا الفاصل الزمني «دقيق» بمعنى أن احتمالية تغطيتها لا تقل أبدًا عن 1 – α الاسمي.
عندما لا تتوفر كميات توزيع جاما، تم اقتراح تقريب دقيق لهذه الفترة الزمنية الدقيقة (بناءً على تحويل ويلسون-هيلفيرتي): [32]
عندما يشير إلى الانحراف القياسي العادي مع منطقة الذيل العليا α / 2 .
لتطبيق هذه الصيغ في نفس السياق على النحو الوارد أعلاه (بالنظر إلى عينة من القيم المقاسة n k i مستمدة من توزيع بواسون بمتوسط λ)، يجب تعيين
احسب الفاصل الزمني لـ μ = nλ، ثم قم باشتقاق الفترة الزمنية لـ λ .
استدلال بايزي
في الاستدلال البايزي، يكون الاتحاد السابق لمعامل المعدل λ لتوزيع بواسون هو توزيع جاما. [33] اسمحوا
تشير إلى أن λ يتم توزيعها وفقًا لكثافة جاما g المحددة من حيث معلمة الشكل α ومعلمة المقياس العكسي β :
بعد ذلك، بالنظر إلى نفس العينة من قيم n المقاسة k i كما كان من قبل، وقبل غاما (α، β)، يكون التوزيع اللاحق
والخلفي يعني E [λ] يقترب تقدير أقصى احتمال في حدود ، والتي تتبع مباشرة من التعبير العام لمتوسط توزيع جاما.
التوزيع التنبئي اللاحق لملاحظة إضافية واحدة هو توزيع سالب ذي الحدين، [34] يُسمى أحيانًا توزيع غاما-بواسون.
التقدير المتزامن لوسائل بواسون المتعددة
افترض هي مجموعة من المتغيرات العشوائية المستقلة من مجموعة من توزيعات بواسون، ولكل منها معلمة و ، ونود تقدير هذه المعلمات. بعد ذلك، أظهر Clevenson و Zidek أنه في ظل خسارة الخطأ التربيعية الطبيعية ، متي ، إذن، على غرار مثال شتاين للوسائل العادية، مقدر MLE غير مقبول.[35]
في هذه الحالة، يتم إعطاء عائلة من مقدر مينيماكس لأي و كـ [36]
الحدوث والتطبيقات
يمكن العثور على تطبيقات توزيع بواسون في العديد من المجالات بما في ذلك: [37]
- مثال عن الاتصالات: وصول المكالمات الهاتفية إلى النظام.
- مثال في علم الفلك: وصول الفوتونات إلى التلسكوب.
- مثال في الكيمياء: توزيع الكتلة المولية لبلمرة حية. [38]
- مثال في علم الأحياء: عدد الطفرات على خيط من الحمض النووي لكل وحدة طول.
- مثال إداري: وصول العملاء إلى العداد أو مركز الاتصال.
- مثال على التمويل والتأمين: عدد الخسائر أو المطالبات التي تحدث في فترة زمنية معينة.
- مثال على علم الزلازل الزلزالية: نموذج بواسون مقارب للمخاطر الزلزالية للزلازل الكبيرة. [39]
- مثال على النشاط الإشعاعي: عدد حالات التحلل في فترة زمنية معينة في عينة مشعة.
- مثال البصريات: عدد الفوتونات المنبعثة في نبضة ليزر واحدة. هذه ثغرة أمنية كبيرة لمعظم بروتوكولات توزيع المفاتيح الكمية المعروفة باسم تقسيم رقم الفوتون (PNS).
ينشأ توزيع بواسون فيما يتعلق بعمليات بواسون. ينطبق على ظواهر مختلفة من الخصائص المنفصلة (أي تلك التي قد تحدث 0، 1، 2، 3... مرات خلال فترة زمنية معينة أو في منطقة معينة) كلما كان احتمال حدوث الظاهرة ثابتًا في الزمان أو المكان. تتضمن أمثلة الأحداث التي يمكن نمذجتها كتوزيع بواسون ما يلي:
- عدد الجنود الذين قتلوا بركلات الخيول كل عام في كل سلاح في سلاح الفرسان البروسي. تم استخدام هذا المثال في كتاب من تأليف لاديسلاوس بورتكيفيتش (1868–1931). [40]
- عدد خلايا الخميرة المستخدمة عند تخمير بيرة غينيس. استخدم هذا المثال ويليام سيلي جوسيت (1876-1937). [41] [42]
- عدد المكالمات الهاتفية التي تصل إلى مركز الاتصال خلال دقيقة. تم وصف هذا المثال من قبل AK Erlang (1878-1929). [43]
- حركة المرور على الإنترنت.
- عدد الأهداف في الألعاب الرياضية التي يشارك فيها فريقان متنافسان. [44]
- عدد الوفيات في السنة في فئة عمرية معينة.
- عدد القفزات في سعر السهم في فترة زمنية معينة.
- في ظل افتراض التجانس، عدد المرات التي يتم فيها الوصول إلى خادم الويب في الدقيقة.
- عدد الطفرات في امتداد معين من الحمض النووي بعد كمية معينة من الإشعاع.
- نسبة الخلايا التي من شأنها أن تكون مصابة في معين وافر من العدوى.
- عدد البكتيريا في كمية معينة من السائل. [45]
- وصول الفوتونات على دائرة البكسل عند إضاءة معينة وخلال فترة زمنية معينة.
- تم التحقيق في استهداف القنابل الطائرة V-1 على لندن أثناء الحرب العالمية الثانية بواسطة آر دي كلارك عام 1946. [46]
أظهر غالاغر في عام 1976 أن أعداد الأعداد الأولية في فترات زمنية قصيرة تخضع لتوزيع بواسون [47] قدمت نسخة معينة من تخمين مجموعة هاردي-ليتلوود الأولية غير المثبتة لهاردي ليتلوود [48] صحيح.
قانون الأحداث النادرة

يرتبط معدل الحدث باحتمالية وقوع حدث في فترة فرعية صغيرة (من الوقت أو المكان أو غير ذلك). في حالة توزيع بواسون، يفترض المرء أن هناك فترة فرعية صغيرة بما فيه الكفاية بحيث يكون احتمال وقوع حدث مرتين «ضئيلاً». مع هذا الافتراض، يمكن للمرء اشتقاق توزيع بواسون من التوزيع ذي الحدين، مع الأخذ في الاعتبار فقط معلومات العدد المتوقع من الأحداث الإجمالية في الفترة الزمنية بأكملها. دع هذا العدد الإجمالي يكون . قسّم الفترة الزمنية بأكملها إلى فترات فرعية من نفس الحجم، مثل هذا > (نظرًا لأننا مهتمون فقط بأجزاء صغيرة جدًا من الفاصل الزمني، فإن هذا الافتراض مفيد). هذا يعني أن العدد المتوقع للأحداث في فترة لكل يساوي . نفترض الآن أن حدوث حدث في الفترة الزمنية بأكملها يمكن اعتباره تجربة برنولي، حيث محاكمة تقابل النظر فيما إذا كان حدث ما يحدث في الفترات الفرعية مع الاحتمال . العدد المتوقع لإجمالي الأحداث في ستكون مثل هذه المحاكمات ، العدد المتوقع لإجمالي الأحداث في الفترة الزمنية بأكملها. ومن ثم، بالنسبة لكل قسم فرعي من الفترة الزمنية، فقد اقتربنا من حدوث الحدث كعملية برنولي للنموذج . كما لاحظنا من قبل، نريد أن ننظر فقط في فترات فرعية صغيرة جدًا. لذلك، نأخذ النهاية على أنها يذهب إلى ما لا نهاية. في هذه الحالة، يتقارب التوزيع ذي الحدين مع ما يُعرف باسم توزيع بواسون بواسطة نظرية حدود بواسون.
في العديد من الأمثلة المذكورة أعلاه - مثل عدد الطفرات في تسلسل معين من الحمض النووي - الأحداث التي يتم عدها هي في الواقع نتائج تجارب منفصلة، وستكون أكثر دقة في نمذجة باستخدام التوزيع ذي الحدين، أي
في مثل هذه الحالات، يكون n كبيرًا جدًا و p صغيرًا جدًا (وبالتالي فإن التوقع np متوسط الحجم). ثم يمكن تقريب التوزيع عن طريق توزيع بواسون الأقل تعقيدًا
هذا التقريب والتي تعرف أحيانا باسم قانون الأحداث النادرة، [49] لأن كل من ن الفردية الأحداث برنولي نادرا ما يحدث. قد يكون الاسم مضللًا لأن العدد الإجمالي لأحداث النجاح في عملية بواسون لا يلزم أن يكون نادرًا إذا لم تكن المعلمة np صغيرة. على سبيل المثال، عدد المكالمات الهاتفية إلى لوحة مفاتيح مزدحمة في ساعة واحدة يتبع توزيع بواسون مع ظهور الأحداث بشكل متكرر للمشغل، لكنها نادرة من وجهة نظر الفرد العادي من السكان الذين من غير المرجح أن يقوموا بذلك. مكالمة إلى لوحة التبديل تلك في تلك الساعة.
تُستخدم كلمة قانون أحيانًا كمرادف لتوزيع الاحتمالات، والتقارب في القانون يعني التقارب في التوزيع . وفقًا لذلك، يُطلق على توزيع بواسون أحيانًا «قانون الأعداد الصغيرة» لأنه التوزيع الاحتمالي لعدد تكرارات حدث نادر الحدوث ولكن توجد فرص كثيرة جدًا لحدوثه. قانون أرقام صغير هو كتاب لادسلاو بورتكيفيز حول توزيع بواسون، التي نشرت في عام 1898. [40] [50]
علاقته بتوزيع الاحتمالات الطبيعي

توزيع بواسون يبدي منحنى غير متماثل لقيم صغيرة لـ . وعندما تكون عددا كبيرا فإن منحنى بواسون سيؤول إلى توزيع احتمالي طبيعي mit und :
عملية نقطة بواسون
ينشأ توزيع بواسون بعدد نقاط عملية نقطة بواسون الموجودة في منطقة محدودة. وبشكل أكثر تحديدًا، إذا كانت D عبارة عن مساحة منطقة ما، على سبيل المثال، الفضاء الإقليدي R d، الذي | D |، المساحة، الحجم، أو بشكل عام، مقياس ليبيسج للمنطقة محدود، وإذا كان N(D) يشير إلى عدد النقاط في D، إذن
انحدار بواسون والانحدار السلبي ذي الحدين
يعد انحدار بواسون والانحدار السالب ذي الحدين مفيدًا للتحليلات حيث يكون المتغير التابع (الاستجابة) هو العدد (0، 1، 2، ...) لعدد الأحداث أو التكرارات في فترة.
تطبيقات أخرى في العلوم
في عملية بواسون، يتقلب عدد الأحداث المرصودة حول متوسطها λ مع الانحراف المعياري . يشار إلى هذه التقلبات على أنها ضوضاء بواسون أو (خاصة في الإلكترونيات) كضوضاء لقطة.
يعتبر ارتباط المتوسط والانحراف المعياري في حساب الأحداث المنفصلة المستقلة مفيدًا علميًا. من خلال مراقبة كيفية اختلاف التقلبات مع الإشارة المتوسطة، يمكن للمرء تقدير مساهمة حدوث واحد، حتى لو كانت هذه المساهمة صغيرة جدًا بحيث لا يمكن اكتشافها مباشرة . على سبيل المثال، يمكن تقدير الشحنة الإلكترونية على الإلكترون من خلال ربط حجم التيار الكهربائي بضوضاء اللقطة. إذا مرت إلكترونات N نقطة في وقت معين t في المتوسط، يكون متوسط التيار ؛ لأن التقلبات الحالية يجب أن تكون بالترتيب (أي الانحراف المعياري لعملية بواسون)، الشحنة يمكن تقديرها من النسبة .
المثال اليومي هو التحبب الذي يظهر عند تكبير الصور ؛ يعود سبب التحبب إلى تقلبات بواسون في عدد حبيبات الفضة المنخفضة، وليس إلى الحبوب الفردية نفسها. من خلال ربط التحبب بدرجة التوسيع، يمكن للمرء تقدير مساهمة حبة فردية (والتي تكون صغيرة جدًا بحيث لا يمكن رؤيتها بدون مساعدة). تم تطوير العديد من التطبيقات الجزيئية الأخرى لضوضاء بواسون، على سبيل المثال، تقدير كثافة عدد جزيئات المستقبل في غشاء الخلية.
في نظرية المجموعة السببية، تتبع العناصر المنفصلة للزمكان توزيع بواسون في الحجم.
الأساليب الحسابية
يطرح توزيع بواسون مهمتين مختلفتين لمكتبات البرامج المخصصة: تقييم التوزيع ، ورسم أرقام عشوائية حسب هذا التوزيع.
تقييم توزيع بواسون
الحوسبة على سبيل المعطى و هي مهمة تافهة يمكن إنجازها باستخدام التعريف القياسي لـ من حيث الدوال الأسية والقوة والعاملة. ومع ذلك، فإن التعريف التقليدي لتوزيع بواسون يحتوي على مصطلحين يمكن أن يفيضان بسهولة على أجهزة الكمبيوتر: λ k و k ! . الجزء من λ k إلى k ! يمكن أن ينتج عنه خطأ تقريب كبير جدًا مقارنة بـ e −λ، وبالتالي يعطي نتيجة خاطئة. من أجل الاستقرار العددي، يجب تقييم دالة كتلة احتمالية بواسون على أنها
وهو مكافئ رياضيًا ولكنه مستقر عدديًا. يمكن الحصول على اللوغاريتم الطبيعي لوظيفة جاما باستخدام وظيفة lgamma في مكتبة C القياسية (إصدار C99) أو R، أو دالة gammaln في ماتلاب أو سي باي، أو دالة log_gamma في فورتران 2008 وما بعده.
توفر بعض لغات الحوسبة وظائف مدمجة لتقييم توزيع بواسون، وهي
- آر لغة برمجة: وظيفة
dpois(x, lambda)؛ - مايكروسوفت إكسل: دالة
بواسون (x, mean, cumulative)، مع علامة لتحديد التوزيع التراكمي ؛ - ماثماتيكا: توزيع بواسون أحادي المتغير كـ
بواسونDistribution[ ]، [51] توزيع بواسون ثنائي المتغير كـMultivariateبواسونDistribution[ ,{ , }].[52]
الرسم العشوائي من توزيع بواسون
المهمة الأقل أهمية هي استخلاص أعداد صحيحة عشوائية من توزيع بواسون مع المعطى .
يتم توفير الحلول من خلال:
- آر: وظيفة
rpois(n, lambda)؛ - مكتبة جنو العلمية (GSL): الوظيفة gsl_ran_بواسون
توليد المتغيرات العشوائية الموزعة بواسون
دونالد كانوث خوارزمية بسيطة لتوليد أرقام عشوائية موزعة بواسون (أخذ عينات أرقام عشوائية زائفة): [53]
algorithm poisson random number (Knuth):
init:
Let L ← e−λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in
[0,1] and let p ← p × u.
while p > L.
return k − 1.
التعقيد خطي في القيمة المرجعة k، والتي تكون في المتوسط. هناك العديد من الخوارزميات الأخرى لتحسين هذا. يتم إعطاء بعضها في آرينز & ديتر، انظر § مراجع أدناه. بالنسبة للقيم الكبيرة لـ λ، قد تكون قيمة L = e −λ صغيرة جدًا بحيث يصعب تمثيلها. يمكن حل هذا عن طريق تغيير الخوارزمية التي تستخدم معلمة إضافية STEP بحيث لا تتدفق e −STEP :
algorithm poisson random number (Junhao,
based on Knuth):
init:
Let λLeft ← λ, k ← 0 and p ← 1.
do:
k ← k + 1.
Generate uniform random number u in
(0,1) and let p ← p × u.
while p < 1 and λLeft > 0:
if λLeft > STEP:
p ← p × eSTEP
λLeft ← λLeft − STEP
else:
p ← p × eλLeft
λLeft ← 0
while p > 1.
return k − 1.
يعتمد اختيار STEP على عتبة الفائض. بالنسبة لصيغة النقطة العائمة ذات الدقة المزدوجة، تكون العتبة قريبة من 700 e، لذا يجب أن تكون 500 خطوة آمنة.
تشمل الحلول الأخرى للقيم الكبيرة لـ أخذ عينات رفض واستخدام تقريب غاوسي.
معكوس تحويل أخذ العينات هي بسيطة وفعالة للقيم صغيرة من λ، وتتطلب رقم عشوائي موحد واحد فقط لكل عينة U. يتم فحص الاحتمالات التراكمية بدورها حتى يتجاوز المرء U.[54]
algorithm Poisson generator based upon
the inversion by sequential
search::505
init:
Let x ← 0, p ← e−λ, s ← p.
Generate uniform random number u in
[0,1].
while u > s do:
x ← x + 1.
p ← p × λ / x.
s ← s + p.
return x.
تاريخ
سيميون بواسون (1781-1840) ونشر مع نظريته الاحتمالية في عمله البحث في احتمالية الأحكام في المسائل الجنائية والمدنية (1837). [55] عمل نظري حول عدد القناعات الخاطئة في بلد معين من خلال التركيز على متغيرات عشوائية معينة N التي تحسب، من بين أمور أخرى، عدد الأحداث المنفصلة (تسمى أحيانًا «الأحداث» أو «الوافدون») التي تحدث خلال فترة زمنية بطول معين. تم إعطاء النتيجة بالفعل في 1711 من قبل أبراهام دي موفر ف يقياس الشرط سواء كان احتمال النجاح في بعض الألعاب معلقًا بشكل عرضي. [56] [57] [58] [6] هذا يجعله مثالًا على قانون ستيجلر وقد دفع بعض المؤلفين إلى القول بأن توزيع بواسون يجب أن يحمل اسم دي مويفر. [59][60]
في عام 1860، قام سيمون نيوكومب بتكييف توزيع بواسون مع عدد النجوم الموجودة في وحدة الفضاء. [61] تم تطبيق عملي آخر لهذا التوزيع بواسطة لاديسلاوس بورتكيفيتش في عام 1898 عندما تم تكليفه بمهمة التحقيق في عدد الجنود في الجيش البروسي الذين قتلوا عرضًا بركلات الحصان. [40] أدخلت هذه التجربة توزيع بواسون في مجال هندسة الموثوقية.
تلخيص التوزيع
المتغير العشوائي X يتبع توزيع بوسون بمعلمه λ إذا كانت دالته الاحتمالية هي:
حيث أن هي معلمة التوزيع الوحيدة بمقدار ثابت، ونعرف المتغير العشوائي
ولكي نتحقق أن (f(x دالة احتمالية
المنوال
إذن تبين لنا أن (f(x دالة متزايدة إذا كانت وأنها متناقصة إذا كانت أما إذا كانت فذلك يعني وعلى ذلك إذا كانت عدد صحيح فيكون هناك منوالان عند أما إذا كانت عدد غير صحيح فيكون المنوال هو العدد الصحيح الذي يأتي فورا بعد .
دالة التوزيع التراكمية
متوسط التوزيع
وحيث أن
إذن
تباين التوزيع
لكي نحصل على تباين بوسون نوجد أولا القيمة المتوقعة
أي أن
إذن
ونستنتج من ذلك أن: التباين = المتوسط =
دالة توزيع العزوم
حيث أن
مثال: إذا كان متوسط عدد الحوادث الأسبوعية على إحدى الطرق في مدينة ما هو 3 حوادث. فما احتمال أن يقع في أحد الأسابيع حادثتين ؟
الحل:
متوسط عدد الحوادث
نفرض أن X عدد الحوادث الأسبوعية إذن
حساب (p(k
يقام حساب هذه الكمية نتيجة عن العمل بتوزيع ثنائي ذا المعلمتين (T ; λ/T). إذا اعتبرنا T كبيرا، فيمكن تبيين أن التوزيع الثنائي نهايته في اللانهاية هو توزيع بواسون.
القيمة المتوقعة والتباين والانحراف المعياري
- القيمة المتوقعة لتوزيع بواسون هي λ
- تباين توزيع بواسون λ
- الانحراف المعياري لتوزيع بواسون هو
ميادين الاستعمال
غالبا ما استعمل توزيع بواسون لحساب أحداث النادرة كانتحار الأطفال، وصول البواخر إلى المرسى أو الحوادث الناتجة عن ركالات الأحصنة في العساكر (دراسة لاديسلاوس بورتكيفيكز)
أما منذ بعض عشرات السنين، امتد استعمال توزيع بواسون إلى ميادين أخرى. فهو يستعمل كثيرا الآن في تكنولوجيات الإتصال (حساب عدد المواصلات في مدّة معينة)، مراقبة الجودة الإحصائية، وصف بعض الظواهر التابعة لميدان التفكيك النووي المشع (تفكيك النواة المشعة يتبع دالة أسية ذات معملة تدعى أيضا λ) وعلم الأحياء والرصد الجوي...
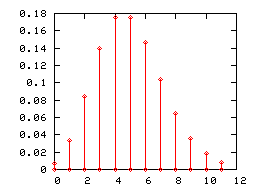
الرسوم البيانة ذات الأعمدة
ككل توزيع قائم على احتمال منفصل، يمكن تمثيل توزيع بواسون برسوم بيانية ذات أعمدة. هنا تحت، تمثل الرسوم البيانية توزيع بواسون ذا المعلمات 1 و2 و5.
رسم توزيع بواسون ذا العامل 5 بدأ يشبه بعض الشيء التوزيع الطبيعي (أو التوزيع الغاوسي) ذا القيمة المتوقعة 5 التباين 5. ولذلك إذا كانت λ أكبر من 5، نخير استعمال نموذج التوزيع الطبيعي.
بعض الخاصيات
إذا كانتا X وY متغيران عشوائيان مستقلاّن يتبعان توزيع بواسون، الأولى مع المعلمة λ والثانية المعلمة μ فإنّ X+Y متغير عشوائي يتبع توزيع بواسون ذا المعلمة λ+μ.
اقرأ أيضا
مراجع
- ^ p963-965, Jan Gullberg, Mathematics from the birth of numbers, W. W. Norton & Company; ISBN 0-393-04002-X ISBN 978-0-393-04002-9
- ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعYates2014 - ^ For the proof, see : Proof wiki: expectation and Proof wiki: variance
- ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعKoehrsen2019 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعUgarte2016 - ^ أ ب ت ث ج ح خ د ذ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعJohnson2005 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعHelske2017 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعChoi1994 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعRiordan1937 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعHaight1967 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعJagadeesan2017 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعLehmann1986 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعRaikov1937 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعvonMises1964 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعLaha1979 - ^ أ ب اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعMitzenmacher2005 - ^ أ ب اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعShort2013 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعKamath2015 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعNIST2006 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعZhang2013 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعZhang2016 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعMcCullagh1989 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعAnscombe1948 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعRoss2010 - ^ "1.7.7 – Relationship between the Multinomial and Poisson | STAT 504". مؤرشف من الأصل في 2019-08-06.
- ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعLoukas1986 - ^ Free Random Variables by D. Voiculescu, K. Dykema, A. Nica, CRM Monograph Series, American Mathematical Society, Providence RI, 1992
- ^ James A. Mingo, Roland Speicher: Free Probability and Random Matrices. Fields Institute Monographs, Vol. 35, Springer, New York, 2017.
- ^ Lectures on the Combinatorics of Free Probability by A. Nica and R. Speicher, pp. 203–204, Cambridge Univ. Press 2006
- ^ Paszek، Ewa. "Maximum Likelihood Estimation – Examples". مؤرشف من الأصل في 2014-05-17.
- ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعGarwood1936 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعBreslow1987 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعFink1976 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعGelman2003 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعClevenson1975 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعBerger1985 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعRasch1963 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعFlory1940 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعLomnitz1994 - ^ أ ب ت اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعvonBortkiewitsch1898 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعStudent1907 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعBoland1984 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعErlang1909 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعHornby2014 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعKoyama2016 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعClarke1946 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعGallagher1976 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعHardy1923 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعCameron1998 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعEdgeworth1913 - ^ "Wolfram Language: PoissonDistribution reference page". wolfram.com. مؤرشف من الأصل في 2020-10-25. اطلع عليه بتاريخ 2016-04-08.
- ^ "Wolfram Language: MultivariatePoissonDistribution reference page". wolfram.com. مؤرشف من الأصل في 2020-08-08. اطلع عليه بتاريخ 2016-04-08.
- ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعKnuth1997 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعDevroye1986 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعPoisson1837 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعdeMoivre1711 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعdeMoivre1718 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعdeMoivre1721 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعStigler1982 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعHald1984 - ^ اكتب عنوان المرجع بين علامتي الفتح
<ref>والإغلاق</ref>للمرجعNewcomb1860
ملاحظات
- توجد جداول للمساعدة على حساب احتمال بمعرفة λ وk. موقع الجدول في ويكي مصدر العربية: جدول توزيع بواسون.
| في كومنز صور وملفات عن: توزيع بواسون |