|
تضامنًا مع حق الشعب الفلسطيني |
قطع ناقص
| هذه المقالةُ جزءٌ من سلسلةِ القطوع المخروطية | |
 | |
| قطع مكافئ | |
|---|---|
| المعادلة | |
| الانحراف المركزي() | |
| البعد البؤري() | |
  | |
| قطع زائد | |
| المعادلة | |
| الانحراف المركزي () | |
| البعد البؤري() | |
  | |
| قطع ناقص | |
| المعادلة | |
| الانحراف المركزي () | |
| البعد البؤري () | |
  | |
| دائرة (حالة خاصة من القطع الناقص) | |
| المعادلة | |
| الانحراف المركزي () | |
| البعد البؤري () | |
 | |
| • • • | |

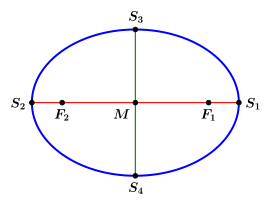
القطع الناقص أو الإهْلِيلَج (بالإنجليزية: Ellipse) هو المنحني المستوي الذي يحقق الخاصية التالية: مجموع بُعد أي نقطة على هذا المنحنى عن نقطتين ثابتين داخله (تسميان البؤرتان) يبقى ثابتا.[1][2][3]
البؤرتان هما النقطتان F1 و F2 في الشكل.
أي يمكن رسم القطع الناقص بواسطة خيط مثبت من طرفيه في نقطتين f1 , f2 ورسم القطع الناقص بالقلم حولهما انطلاقا من النقطة x .

القطع الناقص هو أيضا أحد أنواع القطوع المخروطية، فعند قطع مخروط بمستوى مائل على محور المخروط نحصل على قطع ناقص.
يُهتم بالقطع الناقص بصفة خاصة بسبب أن الأجرام السماوية تسير في أفلاك حول الشمس في مدارات في شكل القطع الناقص، وتحتل الشمس أحد بؤرتيه. هذا ما توصلت إليه قوانين كيبلر. فعند مشاهدة مذنب يأتي من الجزء الخارجي للمجموعة الشمسية منجذبا إلى الشمس تزداد سرعته تدريجيا ثم يُجري منحنيا خلفها ثم يبتعد عنها ثانيا، وتنخفض سرعته اثناء ابتعاده عن الشمس. هذا المسار يكون في شكل قطع ناقص؛ وتكون الشمس في إحدى بؤرتيه.
خواص مماسية

أنظر الشكل 1: النقطة x هي إحدى النقط على القطع الناقص. والنقطتان F1 و F2 هما بؤرتا القطع الناقص. إذا وصـّلنا خيطا طويلا شيئا ما بين البؤرتين وقمنا من النقطة x برسم محيط حولهما نحصل على شكل القطع الناقص.
إذا أقمنا العمودي على خط المماس عند النقطة P فإن العمودي يقسم الزاوية بين الخط xF2 والخط xF1 إلى زاويتين متساويتين (انظر الشكل 1 أو الشكل 3).

دعونا نرى بعض النتائج المترتبة على هذا البيان:
في طاولة بلياردو على شكل إهليلج، إذا القينا كرة على حفتها من إحدى بؤرتيها ستنعكس بالضرورة على البؤرة الأخرى.
والشيء نفسه يحدث في مرآة مقعرة على شكل إهليلج فيه جميع أشعة الضوء المنبعثة من بؤرة تمر بالضرورة بالبؤرة الأخرى بغض النظر عن اتجاه كل شعاع.
وبالمثل، في غرفة على شكل قطع ناقص تصل الموجات الصوتية التي تبدأ في بؤرة إلى البؤرة الأخرى من كل الاتجاهات؛ وبما أن مسافة المسار للوصول من بؤرة إلى أخرى متساوية فإن موجات تصل بشكل متزامنة تماما: هذا ما يفسر أيضا سهولة التواصل السمعي بين شخصين موضوعين في البؤرتين حتى إذا ما كانا متباعدين.
باستخدام خواص القطع الناقص يمكن بناء مسرحا يتمتع فيه جميع الزوار بسماع الصوت منتظما.
المعادلات الجبرية والتباعد المركزي

المحور الأكبر هي المسافة بين a , -a
المحور الأصغر هي المسافة b , -b
PF1+ PF2 =2a
e=PF2/PD
e= معامل التباعد المركزي.
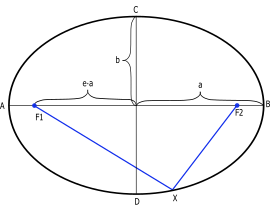
يمكن رسم القطع الناقص في هيئة منحنى في مستوى كارتيزي بالاستعانة بخط خارجه يسمى الدليل D (أنطر الشكل 4):
وفيه ينطبق:
أي أن حاصل ضرب أي خط مثل PD في معامل التباعد المركزي e يساوي الخط PF2.
حيث P هي نقطة على محيط القطع الناقص والمسافة PD هي بعدها عن الدليل D (الخط الرأسي المنقط الأزرق). PD يسقط دائما عموديا على الدليل D .
أي أن الاختلاف المركزي قيمته:
في الرسم البياني الكرتيزي يمكننا تمثيل النقطة بالنقطة على المحورين x , y :
- فتكون إحدى البؤرتين و F1 هي البؤرة الثانية للقطع الناقص.
- بالنسبة إلى معامل التباعد المركزي فهو للقطع الناقص يساوي دائما .
(إذا كانت e=1 ينتج قطعا مكافئا، وإذا كانت e>1 ينتج قطعا زائدا، وإذا كانت e=0 تنتج دائرة) وتجتمع فيها البؤرتان في بؤرة واحدة.) نسبة المسافة بين النقطة P والبؤرة والمسافة بين P والدليل ثابتة وتساوي معامل التباعد المركزي .
يمكن تبسيط معادلة القطع الناقص في النظام الكرتيزي بدلالة القطرين a وb بالمعادلة:
لاحظ العلاقة الخاصة عندما يكون a مساويا لـ b يمكن الحصول على معادلة الدائرة (بوضع )
يعطى معامل التباعد المركزي أيضا بالعلاقة:
كما أن المسافة من أي من البؤرتين إلى المركز C هي حاصل الضرب , وهي تساوي أيضا
يمكن إعادة تعريف القطع الناقص عندما تنزاح محاوره عن نقطة الأصل إلى نقطة على الصورة:
طرق رسم القطع الناقص

هناك العديد من الطرق منها مايلي.
طريقة الخيط والمسمارين

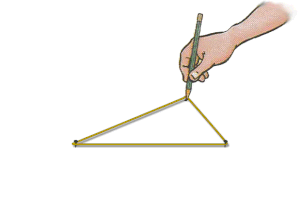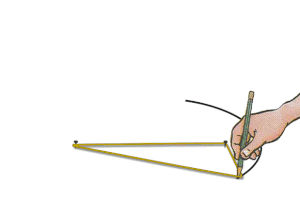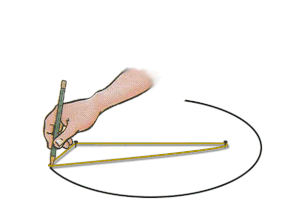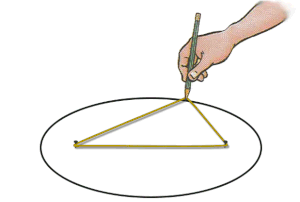
تعتبر هذه الطريقة من أدق الطرق المستعملة في رسم القطاعات الناقصة كما تتميز بسهولة استخدامها إذ تعتمد فقط على تحريك خيط مثبت بين مسمارين. لرسم قطع ناقص يمكن اتباع التعريف والستعانة بخيط مرن (مثل خيط إبرة الخياط) وعمل الاتي:
- من تعريف القطع الناقص فإن مجموع أي ضلعين ممتدين من البؤرة وملتقيان في الطرف الآخر على المحيط يكون ثابتا (أزرق). وهذا يمثل طول الخيط الإجمالي L.
- لتحديد طول الخيط L ينطبق .
- لتحديد البعد بين البؤرتين المراد تثبيت طرفي الخيط عليهما نعلم أن القطع الناقص يميزه اختلاف مركزي يساوي e .
- الآن بمعرفة البعد بين البؤرتين يمكن تثبيت الخيط بمسمارين البعد بينهما يساوي 2a. e والبدء بتحريك قلم أو أداة الرسم لتنزلق حول الخيط المشدود وتكمل محيطا مغلقا.
الاختلاف المركز e للقطع الناقص قيمته دائما بين 0 و 1 .
وفي الحالة الخاصة عندما تكون e=0 يكون الناتج دائرة.
لهذ نسمي e معامل التباعد المركزي.
طريقة المسطرة والإطار

في هذه الطريقة تثقب المسطرة من نقطة غير الوسط (لغير الدائرة) وتنزلق بين ضلعي إطار متعامدين. إذا وضع قلم الرسم مثلا داخل الثقب سيتم رسم ربع قطع الناقص في كل انزلاق مكتمل.
طريقة الاسطوانة المقطوعة
تتمثل هذه الطريقة في عمل اسطوانة دائرية قطرها يساوي القطر الأصغر للقطع المطلوب ثم يتم قطعها (بالمنشار مثلا) بشكل مائل بحيث يكون امتداد طوله مساوي طول القطر الأكبر في القطع الناقص. يصبح السطح المقطوع صورة مثالية للقطع الناقص ويمكن رسم القطع حوله عند تثبيته على ورقة الرسم.
الطرق العددية
يمكن الاستعانة بالتعريف الرياضي للقطع الناقص ورسم نقاط معينة لـ x و y بدلالة a وb. حيث يمكن تبسيط التعريف الأصلي إلى:
عند وجود عدد كاف من النقاط لكل زوج (x,y) يمكن بوصل النقاط واحدة تلو الأخرى الحصول على صورة تقريبية للقطع الناقص. توجد طرق تقريبية أخرى مثل الدائرتين والشعاع والمماس.
الصيغة البارامترية


باستخدام معادلات حساب المثلثات يمكن صيغة القطع الناقص
- حيث:
ترجع الإحداثية t المستخدمة في الرسم إلى عالم الرياضيات فيليب دي لاهير.[5]
حيث:
- t متغير بارامتري (ليس زاوية حقيقية)
مساحة القطع الناقص
تساوي مساحة القطع الناقص :
حيث و هما طولا نصف المحور الأكبر والأصغر، على التوالي. صيغة المساحة بديهية: نبدأ بدائرة نصف قطرها (لذا فإن مساحتها هي ) ونضربها في المعامل لعمل القطع الناقص . من السهل أيضًا إثبات صيغة المساحة بدقة باستخدام التكامل على النحو التالي. يمكن كتابة معادلة القطع الناقص على النحو التالي . من أجل ، هذا المنحنى هو النصف العلوي للقطع الناقص. لذا فإن ضعف تكامل على المجال سيكون ضعف مساحة القطع الناقص:
التكامل الثاني هو مساحة دائرة نصف قطرها ، أي . إذن:
محيط القطع الناقص
ليكن a نصف محوره الكبير وb نصف محوره الصغير، يُحسَب محيط القطع الناقص بتطبيق هذا القانون:
حيث هو معامل التباعد المركزي، و هو التكامل الإهليلجي التام من النوع الثاني:
- تعبير عن المحيط بواسطة المتسلسلة اللانهائية:
حيث n!! هو عاملي ثنائي.

وبطريقة أشمل
كما تعطي طريقة رامانجن تقريبا أفضل:
وبتقريب آخر:
كحالة خاصة عندما يكون القطر الأصغر نصف الأكبر:
وبتقريب مكتسب عمليا:
شروط المماس
خط متماس لقطع ناقص عند إحدى نقاطه
معلوم قطع ناقص دلتا ونقطة P تنتمي إليه. مطلوب تحديد الخط p المتماس لدلتا في النقطة P. وبعبارة أخرى ، مطلوب تحديد الخط القطبي p لـلنقطة القطبية P بالنسبة لدلتا.
الطريقة (هندسة وصفية)
- يتم تمرير بالنقطة P أي خط مستقيم b (أو c) بحيث يقطع دلتا
- يتم تحديد القطب B ل b بالنسبة لدلتا
- يتم توصيل النقطتان P و B للحصول على الخط المطلوب p
استنتاج: إن النقاط القطبية لحزمة الخطوط التي تمر بالنقطة P، تنتمي للخط القطبي p. [6]

معرض
-
تحديد المسافتين الأدنى الأقصى (الملونتين بالاحمر والاصفر) بين إهليلجين غير متشابهين (الملونين بالارجواني)[7]
-
مقطع إهليجي
انظر أيضًا
- لا مركزية (رياضيات)
- بيضوي
- قطع مخروطي
- مخروط
- إسطوانة
- سطح ناقص
- نصف المحور الرئيسي
- نظام إحداثيات إهليلجي
- منحنى حلقي، منحنى موازي للإهليلج
- مرسمة قطع ناقص
مراجع
- ^ Chamberlain, G. (فبراير 1983). "A characterization of the distributions that imply mean—Variance utility functions". ج. 29 ع. 1: 185–201. DOI:10.1016/0022-0531(83)90129-1. مؤرشف من الأصل في 2018-09-28.
{{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب|دورية محكمة=(مساعدة) - ^ Bessel، F. W. (2010). "The calculation of longitude and latitude from geodesic measurements (1825)". Astron. Nachr. ج. 331 ع. 8: 852–861. arXiv:0908.1824. DOI:10.1002/asna.201011352.
- ^ E. Hartmann: Lecture Note 'Planar Circle Geometries', an Introduction to Möbius-, Laguerre- and Minkowski Planes, p. 55 نسخة محفوظة 15 ديسمبر 2017 على موقع واي باك مشين.
- ^ المرجع:Lezioni Di Geometria Proiettiva Di Federigo Enriques p. 226 نسخة محفوظة 17 أغسطس 2020 على موقع واي باك مشين.
- ^ K. Strubecker: Vorlesungen über Darstellende Geometrie, GÖTTINGEN, VANDENHOECK & RUPRECHT, 1967, p. 26
- ^ Geometric Loci نسخة محفوظة 2022-09-22 على موقع واي باك مشين.
- ^ determine the minimum and maximum distances between two non-homothetic conics نسخة محفوظة 6 نوفمبر 2021 على موقع واي باك مشين.
| جزء من سلسلة مقالات حول |
| الهندسة الرياضية |
|---|
 |
| علماء الهندسة |
| بوابة هندسة رياضية |
| في كومنز صور وملفات عن: قطع ناقص |
![تحديد المسافتين الأدنى الأقصى (الملونتين بالاحمر والاصفر) بين إهليلجين غير متشابهين (الملونين بالارجواني)[7]](https://upload.wikimedia.org/wikipedia/commons/thumb/a/a4/Distanza-min-max-2-coniche-non-omotetiche.jpg/104px-Distanza-min-max-2-coniche-non-omotetiche.jpg)
