قوس الظل

دالة قوس الظل
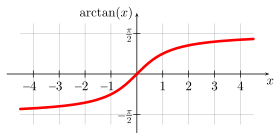
التمثيل البياني للدالة التمثيل البياني للدالة
تدوين	$\arctan x$
دالة عكسية	$\tan x$ على المجال $]-\frac{\pi }{2},\frac{\pi }{2}[$
مشتق الدالة	$\frac{1}{1+x^2}$
مشتق عكسي (تكامل)	$x\arctan x-\frac{1}{2}\ln (1+x^2)+C$
الميزات الأساسية
زوجية أم فردية؟	فردية
مجال الدالة	$\mathbb{R}$
المجال المقابل	$]-\frac{\pi }{2},\frac{\pi }{2}[$
قيم محددة
القيمة/النهاية عند الصفر	0
نهاية الدالة عند +∞	$\frac{\pi }{2}$
نهاية الدالة عند -∞	$-\frac{\pi }{2}$
خطوط مقاربة	$y=\frac{\pi }{2}$ عند $+\mathrm{\infty }$ $y=-\frac{\pi }{2}$ عند $-\mathrm{\infty }$
جذور الدالة	0
نقاط ثابتة	0

في الرياضيات، دالة قوس الظل (بالإنجليزية: Arctangent)‏ لعدد حقيقي المعرفة على $\mathbb{R}$ هي الدالة العكسية لدالة الظل، مستقرها هو $]-\frac{\pi }{2},\frac{\pi }{2}[$، وحدتها هي الراديان.

الدالة التي ترفق بكل عدد حقيقي، قيمة قوس الظل الخاص به يرمز لها بـ arctan أو tan ^-1. ومن ثم تكون الدالة العكسية لدالة الظل المثلثية المقتصرة إلى المجال $]-\frac{\pi }{2},\frac{\pi }{2}[$ .

في المَعْلم الديكارتي المتعامد والمتجانس (متعامد ممنظم) للمستوي، يتم الحصول على التمثيل البياني لدالة قوس ظل الزاوية انطلاقا من التمثيل البياني لدالة الظل المقتصرة إلى المجال $]-\frac{\pi }{2},\frac{\pi }{2}[$ بانعكاس حول المحور ذو المعادلة y = x.

مشتق

دالة الظل العكسية تقبل الإشتقاق على $\mathbb{R}$ ودالتها المشتقة هي:

${{\arctan }^{\prime }}^{\prime }x=\frac{1}{1+x^2}$

إثبات

يمكننا كتابة مشتقة الدالة بهذه الصيغة:$(\arctan x{)}^{\prime }=\frac{d}{dx}\arctan x$

نضع $\theta =\arctan x$:

$\frac{d\theta }{d\tan \theta }=\frac{d\theta }{d\theta (1+{\tan }^2\theta )}=\frac{1}{1+{\tan }^2\theta }=\frac{1}{1+x^2}$

إثبات آخر

يمكن استنتاج مشتقة قوس الظل كالتالي:

1. معلوم أن tan(arctan(x))=x بتفاضل الطرفين:

$(\tan (\arctan (x){)}^{\prime }=x^{\prime }$

نحصل على :

$(\tan (\arctan (x){)}^2+1)\frac{d}{dx}\arctan (x)=1$

بتبسيط tan(arctan(x)) نحصل على:

$(x^2+1)\frac{d}{dx}\arctan (x)=1$

و بترتيب التعبير نحصل على مشتقة دالة قوس الظل :

$\frac{d}{dx}\arctan (x)=\frac{1}{1+x^2}$

تمثيل بواسطة متسلسلة

يمكننا تمثيل الدالة بواسطة متسلسلة تايلور:

$\mathrm{\forall }x\in [-1,1]\arctan x=\sum _{k=0}^{\mathrm{\infty }}(-1{)}^k\frac{x^{2k+1}}{2k+1}=x-\frac{1}{3}{x}^3+\frac{1}{5}{x}^5-\frac{1}{7}{x}^7+\cdots$.

المشتق العكسي

يتم الحصول على المشتق العكسي لدالة قوس الظل عن طريق التكامل بالتجزئة :

$x\arctan x-\frac{1}{2}\ln (1+x^2)+C$

على المستوي العقدي

الشكل اللوغاريتمي

يمكننا التعبير عن دالة قوس الظل باستخدام اللوغاريتم العقدي:

$\mathrm{\forall }x\in \mathbb{C}\setminus (i(]-\mathrm{\infty },-1]\cup [1,+\mathrm{\infty }[))\arctan x=\frac{1}{i}\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}(ix)=\frac{1}{2i}\ln (\frac{1+ix}{1-ix})=\frac{\ln (1+ix)-\ln (1-ix)}{2i}$

حيث $\mathrm{a}\mathrm{r}\mathrm{t}\mathrm{a}\mathrm{n}\mathrm{h}x$ هي دالة الظل الزائدية العكسية.

تمثيل الدالة العقدية

التمثيل البياني اللوني للدالة $\arctan z$

طالع أيضًا

• دوال مثلثية عكسية
• قوس الجيب
• قوس جيب التمام
• قوس الظل ثنائي العمدة