|
تضامنًا مع حق الشعب الفلسطيني |
ط (رياضيات)
ط (رياضيات) |
تحوي هذه المقالة أو هذا القسم ترجمة آلية. |
| جزء من سلسلة مقالات حول |
| الثابت الرياضي π |
|---|

باي () أو ط[1] أو ثابت الدائرة هو ثابت رياضي. عُرف في الأصل على أنه نسبة محيط الدائرة إلى قطرها، والآن لدى تعريفات معادلة مختلفة. تظهر في العديد من الصيغ في جميع مجالات الرياضيات والفيزياء. وتساوي تقريبًا ...3.14159.
مُثل بالحرف اليوناني "" منذ منتصف القرن الثامن عشر، على الرغم من أنه مكتوب أحيانًا "pi". ويسمى أيضا ثابت أرخميدس.
عدد غير نسبي. لهذا السبب، لا يمكن التعبير عنه على شكل كسر أي لا يمكن كتابته على صورة حيث a وb عددان صحيحان. نتيجة لذلك، تمثيله العشري لا ينتهي ولا يستقر أبدًا في نمط تكراري منتظم. ومع ذلك، فإن كسورًا مثل 22/7 وأعدادًا حقيقية أخرى تستخدم لتقريب العدد . يبدو أن الأرقام بعد الفاصلة موزعة عشوائيًا. على وجه الخصوص، يتم تخمين تسلسل أرقام لمقاربة نوع معين من العشوائية الإحصائية، ولكن حتى الآن، لم يكتشف أي دليل على ذلك. أيضًا، هو عدد متسام؛ بمعنى أنه ليس جذر أي متعدد الحدود له معاملات كسرية. يعني هذا التعالي أنه من المستحيل حل التحدي القديم المتمثل في تربيع الدائرة باستخدام إنشاءات الفرجار والمسطرة.
حسبت الحضارات القديمة قيمًا دقيقة إلى حد ما أن تقارب لأسباب عملية، بما في ذلك المصريون والبابليون. حوالي 250 قبل الميلاد، أنشأ عالم الرياضيات اليوناني أرخميدس خوارزمية لحسابها. في القرن الخامس الميلادي تقريبًا، كانت الرياضيات الصينية تقارب إلى سبعة أرقام، في حين قدمت الرياضيات الهندية تقريبًا من خمسة أرقام، وكلاهما استخدم التقنيات الهندسية. الصيغة التاريخية الأولى بالضبط لـ، المستندة إلى سلسلة لانهائية، لم تكن متاحة إلا بعد ألف عام، عندما اكتُشفت سلسلة مادهافا-لايبنتس في القرن الرابع عشر في الرياضيات الهندية.[2][3] في القرنين العشرين والواحد والعشرين، اكتشف علماء الرياضيات وعلماء الحاسوب مقاربات جديدة. عندما اقترنت بزيادة القدرة الحسابية، وسّعت التمثيل العشري لـ إلى العديد من تريليونات من الأرقام بعد العلامة العشرية.[4][5] لا تتطلب جميع التطبيقات العلمية في الواقع أكثر من بضع مئات من الأرقام من ، وعدد أقل بكثير. الدافع الأساسي لهذه الحسابات هو السعي لإيجاد خوارزميات أكثر كفاءة لحساب سلسلة رقمية طويلة، وكذلك الرغبة في تحطيم الأرقام القياسية.[6][7] كما استُخدمت الحسابات الشاملة المعنية لاختبار أجهزة الحاسوب العملاقة وخوارزميات الضرب عالية الدقة.
نظرًا إلى كون التعريف الأول ل متعلقًا بالدائرة، فإنه يوجد في العديد من الصيغ في علم المثلثات والهندسة، وخاصة تلك المتعلقة بالدوائر والقطع الناقص. بالإضافة إلى ذلك، يظهر في مجالات الرياضيات والعلوم التي ليس لها علاقة تذكر بهندسة الدوائر، مثل نظرية الأعداد والإحصاء، وكذلك في جميع مجالات الفيزياء تقريبًا. يجعلها واحدة من أكثر الثوابت الرياضية المعروفة على نطاق واسع داخل وخارج المجتمع العلمي. نُشرت العديد من الكتب المخصصة لـ، وغالبًا ما تؤدي حسابات وضع الأرقام القياسية إلى عناوين الأخبار. أدت محاولات حفظ قيمة بدقة متزايدة إلى تسجيل أكثر من 70000 رقم.
الأساسيات
الاسم



الرمز المستخدم من طرف علماء الرياضيات من أجل تمثيل النسبة بين محيط الدائرة وقطرها هو الحرف الإغريقي و يُقرأ هذا الحرف باي[8] و لا ينبغي خلط هذا العدد مع الحرف Π، والذي يعني الجداء. ويُنطق في اللغة الإنجليزية (/paɪ/).[9]
وكان أول عالم رياضيات استعمل الحرف الإغريقي من أجل تمثيل نسبة محيط الدائرة على قطرها هو ويليام جونز، الذي استعملها في عام 1706 في عمل له.
التعريف

هي نسبة محيط الدائرة C على قطرها d:[10]
نسبة C/d هي ثابتة بغض النظر عن محيط أو مساحة الدائرة. هذا التعريف ل يستعمل بشكل غير مباشر مفهوم الهندسة الأقليدية المسطحة. رغم أن مفهوم الدائرة قد يمدد إلى الهندسة غير الإقليدية المنحنية، فإن هذه الدوائر الجديدة لا تحقق المعادلة . هناك تعريفات أخرى لا تستعمل نهائيا الدوائر. على سبيل المثال، هو ضعف أصغر عدد موجب حيث تنعدم دالة الجيب التمام.
محيط الدائرة هو طول القوس المحيط بالدائرة، وهي كمية يمكن تعريفها رسميًا بشكل مستقل عن الهندسة باستخدام الحدود، وهو مفهوم في حساب التفاضل والتكامل.[11] على سبيل المثال، يمكن للمرء أن يحسب مباشرة طول القوس للنصف العلوي من دائرة الوحدة، الوارد في الإحداثيات الديكارتية بالمعادلة x2 + y2 = 1، باعتبارها التكامل:[12]
الخصائص

π عدد غير كسري. هذا يعني أنه لا يمكن كتابته على شكل نسبة عددين صحيحين، مثل 22/7، أو أي كسر آخر مستعمل تقريبًا للباي. ولهذا السبب، فإن π عدد غير منته من الأرقام بعد الفاصلة في تمثيله العشري، وأنه لا توجد أي سلسلة من الأرقام تتكرر بشكل غير منته. هناك عدة البرهان على أن باي عدد غير كسري.
π عدد متسام. هذا يعني أنه لا يمكن أن يكون جذرا لأي متعددة حدود غير منعدمة عواملها أعداد كسرية، كما هو الحال بالنسبة لمتعددة الحدود . لتسامي π نتيجتان مهمتان أولهما: لا يمكن أن يُعبر عن π بأي دمج لأعداد كسرية وجذور مربعة وجذور مكعبة وما يشبه ذلك مثل أو . أما ثانيهما، فهو بما أنه يُستحال انشاء عدد متسام بواسطة البركار والمسطرة، كذلك من المستحيل تربيع الدائرة.
الكسور المستمرة
العدد ط، كونه عددا غير كسري، لا يمكن تمثيله كسرا بسيطا. هذه الخاصية تبقى صحيحة بالنسبة لجميع الأعداد غير الكسرية. ولكن الأعداد غير الكسرية، بما في ذلك ط، يمكن تمثيلها بكسور متكررة تسمى الكسور المستمرة:
ايقاف هذا الكسر المستمر في مستوى ما يعطي تقريبا معينا للعدد ط. استعمل الكسران 22/7 و 355/113 عبر التاريخ من أجل إعطاء قيمة مقربة للعدد ط. رغم عدم وجود أي انتظام أو تكرار في الكسر المستمر البسيط الذي يعطي قيمة العدد ط، فإن علماء الرياضيات وجدوا كسورا مستمرة معممة تحتوي على سلاسل عددية منتطمة أو متكررة. مثالا الكسور المستمرة التالية:
قيمة مقربة
قيمة التقريبية حتى 1000 مرتبة عشرية:
3.1415926535897932384626433832795028841971693993751058209749445923078164062862089986280348253421170679 8214808651328230664709384460955058223172535940812848111745028410270193852110555964462294895493038196 4428810975665933446128475648233786783165271201909145648566923460348610454326648213393607260249141273 7245870066063155881748815209209628292540917153643678925903600113305305488204665213841469519415116094 3305727036575959195309218611738193261179310511854807446237996274956735188575272489122793818301194912 9833673362440656643086021394946395224737190702179860943702770539217176293176752384674818467669405132 0005681271452635608277857713427577896091736371787214684409012249534301465495853710507922796892589235 4201995611212902196086403441815981362977477130996051870721134999999837297804995105973173281609631859 5024459455346908302642522308253344685035261931188171010003137838752886587533208381420617177669147303 15982534904287554687311595628638823537875937519577818577805321712268066130019278766111959092164201989
التاريخ
في العصور القديمة والوسطى
من غير المعروف كيف ومتى اكتشف الإنسان أن النسبة بين محيط الدائرة وقطرها هي نسبة ثابتة، لكن من الأكيد أن هذه الحقيقة قد عرفت منذ قديم الزمان. فالحضارات القديمة كالحضارة المصرية والبابلية تعاملت مع ط. كان البابليون يستخدمون التقريب بينما استخدم المصريون التقريب .[13] ويرجع حصر قيمة بين و إلى العالم اليوناني أرخميدس الذي ابتكر طريقة الاستنفاذ لحساب قيمة تقريبية للعدد ط.
في القرون التالية اهتم الفلكيون بتدقيق الحساب التقريبي لـ ط، وأوجد الفلكيون الهنود والصينيون عدة صيغ للقيمة التقريبية، وشارك العلماء العرب والمسلمون في تحسين تلك الصيغ، فتوصل غياث الدين جمشيد الكاشي في القرن الخامس عشر لحساب قيمة تقريبية صحيحة حتى ستة عشر رقما عشريا، وكان ذلك قبل ظهور الآلات الحاسبة بأربعمائة سنة.
عصر التقريب بمتعددي الأضلع

اعتمدت أول خوارزمية مسجلة في التاريخ والتي تمكن من حساب قيمة π بصفة دقيقة على مقاربة هندسية تستعمل متعددي الأضلع. كان ذلك في عام حوالي 250 قبل الميلاد من طرف عالم الرياضيات الإغريقي أرخميدس. بقيت هذه الطريقة المعتمدة على متعددي الأضلع هي الطريقة الأساسية من أجل حساب π لمدة تزيد عن الألف سنة. نتيجة لذلك، كان يشار في بعض الأحيان إلى π على أنها ثابتة أرخميدس.

في عام 1424، تمكن غياث الدين الكاشي من حساب ما يكافئ ستة عشر رقما بعد الفاصلة ل π، بالاستعانة بمتعدد للأضلاع عدد أضلاعه يساوي 3×228. بقي هذا العمل الأكثر دقة في العالم لمدة تقارب 180 سنة.
المتسلسلات غير المنتهية

تطور حساب ط بشكل هائل في القرنين السادس عشر والسابع عشر بفضل اكتشاف المتسلسلات غير المنتهية، والتي هي مجاميع تحتوي على عدد غير منته من الحدود.
أول متسلسلة غير منتهية اكتشفت في أوروبا كانت جداء غير منته (بدلا من مجموع غير منته كما جرت العادة من أجل حساب العدد ط)، اكتشفها عالم الرياضيات الفرنسي فرانسوا فييت عام 1593:
تسمى هذه المتسلسلة صيغة فييت.
ثاني متسلسلة غير منتهية اكتشفت في أوروبا، وجدها جون واليس في عام 1655. وكانت هي أيضا جداء غير منته. تسمى هذه المتسلسلة جداء واليس.
في أوروبا، أُعيد اكتشاف صيغة مادهافا من طرف عالم الرياضيات السكوتلاندي جيمس غريغوري في عام 1671 ومن طرف لايبنز في عام 1674.
هاته الصيغة، المعروفة باسم متسلسلة غريغوري-لايبنز، تساوي عندما يساوي z واحدا.
في عام 1706، استعمل جون ماشن متسلسلات غريغوري-لايبنز فوجد خوارزمية تؤول إلى العدد ط بسرعة أكبر من سابقاتها.
باستعمال هاته الصيغة، وصل ماشن إلى مائة رقم عشري بعد الفاصلة عند إعطائه لتقريب للعدد ط. وهي الطريقة التي استعملت فيما بعد في أجهزة الحاسوب وحتى عهد قريب. انظر صيغة مشابهة لصيغة ماشن.
سرعة الاقتراب
| متسلسلات تحسب قيمة | بعد الدورة الأولى | بعد الدورة الثانية | بعد الدورة الثالثة | بعد الدورة الرابعة | بعد الدورة الخامسة | تؤول إلى : |
|---|---|---|---|---|---|---|
| 4.0000 | 2.6666... | 3.4666... | 2.8952... | 3.3396... | = 3.1415... | |
| 3.0000 | 3.1666... | 3.1333... | 3.1452... | 3.1396... |
كون π عددا غير كسري وكونه عددا متساميا
لم يكن الهدف الوحيد من تطور الرياضيات المتعلقة ب π هو حساب أكبر قدر ممكن من الأرقام في تمثيلها العشري. عندما حل أويلر معضلة بازل عام 1735، واجدا بذلك القيمة الدقيقة لمجموع مقلوبات مربعات الأعداد الصيحيحة الطبيعية، أثبت وجود علاقة وطيدة بينها وبين الأعداد الأولية. ساهم ذلك فيما بعد، بتطور ودراسة دالة زيتا لريمان.
برهن العالم السويسري يوهان هاينريش لامبرت في عام 1761 أن π عدد غير كسري، مما يعني أنه لا يمكن أن يساوي نسبة عددين صحيحين. استعمل برهان لامبرت تمثيلا بالكسور المستمرة لدالة الظل. برهن عالم الرياضيات الفرنسي أدريان ماري ليجاندر في عام 1794 أن هو أيضا عدد غير كسري. في عام 1882، برهن عالم الرياضيات الألماني فيردينوند فون ليندمان أن π عدد متسام، مثبتا بذلك حدسية كل من ليجاندر وأويلر.
عصر الحاسوب والخوارزميات التكرارية

مع ظهور الآلات الحاسبة ثم الحاسبات الإلكترونية والنظرية الرياضية للنهايات والمتسلسلات اللانهائية تحسنت قدرة العلماء على حساب قيم تقريبية للعدد ط، ووصل السجل العالمي حتى عام 2002 إلى أكثر من تريليون رقم عشري. الجدير بالذكر أن فابريس بيلارد حطم رقما قياسيا جديدا في 31 ديسمبر 2009 حين قام بحساب هذا العدد على حاسوب شخصي إلى 2.7 ترليون مرتبة عشرية، وقد استغرقه الحساب 131 استخدم خلالهاأسرع خوارزمية على الإطلاق حتى اليوم وكتب الشفرة المصدرية بلغة سي.[15][16]
الهدف من حساب ط
حساب مساحات وأحجام الأشكال الهندسية المعتمدة على الدائرة كالقطع الناقص والكرة والمخروط والاسطوانة
المتسلسلات المتقاربة بسرعة

خوارزميات الحنفية
اكتشفت خوارزميتان في عام 1995، فتحتا بابا واسعا للبحث المتعلق بالعدد ط. هاتان الخوارزميتان تسميان بخوارزميات الحنفية لأنها كسيلان الماء من حنفية، تنتج أرقاما في التمثيل العشري للعدد ط، لا تستعمل ولا يُحتاج إليها بعد حسابها.
اكتشفت خوارزمية حنفية أخرى في عام 1995، وهي خوارزمية BBP لاستئصال الأرقام العشرية. تم اكتشافها من طرف سيمون بلوف.
كونها بصيغة كسرية يمكن بها استخلاص الأرقام السداسية عشر والثنائية دون حساب سابقاتها وبها أمكن الوصول إلى 1,000,000,000,000,000 مرتبة ثنائية.
الاستعمال
في الهندسة وحساب المثلثات
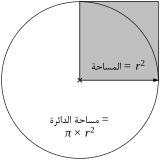

يظهر العدد ط في حساب مساحات وأحجام الأشكال الهندسية المعتمدة على الدائرة كالقطع الناقص والكرة والمخروط والطارة. فيما يلي، بعض من الصيغ الأكثر أهمية والتي تحتوي على العدد ط :
- محيط دائرة شعاعها r هو .
- مساحة دائرة شعاعها r هي .
- حجم كرة شعاعها r هو .
- مساحة كرة شعاعها r هو .
طريقة مونت كارلو
طرق مونت كارلو من أجل ايجاد قيمة مقربة للعدد ط بطيئة جدا مقارنة مع طرق أخرى، وبالتالي، لا تستعمل أبدا إذا كانت السرعة والدقة هما المطلوبتان.
في الأعداد العقدية والتحليل

كل عدد عقدي، يمكن أن يُعبر عنه باستعمال عددين حقيقين. في النظام الإحداثي القطبي، يستعمل عدد حقيقي r (الشعاع أو نصف القطر) من أجل تمثيل المسافة بين z وأصل المعلم في المستوى العقدي. ويستعمل عدد حقيقي ثان (الزاوية أو φ) يمثل كمية الدوران في عكس اتجاه عقارب الساعة، انطلاقا من نصف محور الأراتيب المحتوي على الأعداد الحقيقية الموجبة ووصولا إلى z ذاته، كما يلي:
حيث i هي الوحدة التخيلية التي تحقق i2 = −1. الظهور المكثف للعدد ط في التحليل العقدي قد يكون مرتبطا بالدالة الأسية لمتغير عقدي، كما وصفت ذلك صيغة أويلر :
حيث الثابتة e هي أساس اللوغارتم الطبيعي. في هاته الصيغة، عندما يكون φ مساويا ل π، تنتج صيغة أويل متطابقة أويلر، التي نظر إليها علماء الرياضيات كثيرا لاحتوائها على الثابتات الرياضياتية الخمسة، الأكثر أهمية:
يوجد n عدد مركب تختلف عن بعضا البعض z يحققن المعادلة zn = 1. تسمى هذه الأعداد بالجذور النونية للوحدة، وتحدد بواسطة الصيغة التالية:
في نظرية الأعداد ودالة زيتا لريمان
دالة زيتا لريمان (ζ(s هي دالة مستعملة في مجالات عديدة من الرياضيات. عندما يكون s مساويا ل 2، يمكن أن تكتب كما يلي :
كان ايجاد قيمة هذه المتسلسلة غير المنتهية معضلة مشهورة في الرياضيات، تدعى معضلة بازل. حلحلها ليونهارد أويلر عام 1735 حيث برهن أنها تساوي . هاته النتيجة أدت إلى نتيجة أخرى في نظرية الأعداد وهي كون احتمال أن يكون عددان طبيعيان، اختيرا عشوائيا، أوليين فيما بينهما، مساويا ل .
يمكن لهذا الاحتمال أن يستعمل، بالإضافة إلى مولد للأعداد العشوائية، من أجل إعطاء قيمة مقربة ل ، اعتمادا على طريقة مونتي كارلو.
في الفيزياء
يمكن رؤية العدد ط أو π في العديد من القوانين الفيزيائية من أهمها:
- مبدأ الريبة، الذي ينص على أن قياس موضع جسيم (Δx) وكمية التحرك (Δp) لايمكن لكليهما أن يكونا صغيرين في نفس الوقت:[18]
- قانون كولوم للقوة الكهربائية، يصف القوة بين شحنتين كهربائيتين(q1 وq2) تفصلهما مسافة r:[20]
- قوانين كبلر، التي تربط بين الزمن المداري (P) والمحور الإهليجي الأكبر a والكتل(M وm) لجسمين مداريين حول بعضهما:
في الاحتمالات والإحصاء

ƒ(x) = e−x2. المنطقة الملونة بين منحنى الدالة ومحور y لها مساحة تساوي .
في علم الاحتمالات والإحصاء، توجد العديد من التوزيعات التي تحوي العدد π، منها ما يلي:
- دالة الكثافة الاحتمالية لتوزيع كوشي:[23]
صيغ حسابية للعدد ط
توجد طرق عديدة ومختلفة لنشر وحساب العدد ط منها النشر بواسطة سلاسل تايلور وماكلورين، النشر بواسطة متسلسلات فوريير، النشر بالنظام الثنائي، والنشر بالكسور المستمرة.
النشر بواسطة متسلسلة ماكلورين
إحدى المعادلات المعروفة لإيجاد ط هي :
ويمكن استنتاج هذه الصيغة من متسلسلة ماكلورين لدالة قوس الظل (بالإنجليزية: arctan) حيث
في الحقيقة لاتستخدم الالات الحسابية السلسلة السابقة (عند تعويض x =1) بسبب تقاربها البطيء ويمكن ملاحظة ذلك عند الوصول إلى رقم المليون وواحد مثلا ستكون الدقة لاتتجاوز خمس مراتب عشرية، وهكذا.
يمكن استعمال الصيغة الرياضية عند تعويضات x أكبر من الواحد للحصول على تقارب أسرع مثل:
سلاسل أخرى
هناك حسابات أخرى مثل:
اما في العصر الحديث فقد ظهرت خوارزميات أكثر تقاربا بكثير مثل:
- سلسلة رامانجن:
- سلسلة الإخوان شودنوفسكي التي سمحت لأول مرة تقريب ط لمليار مرتبة عشرية عام 1989 باستخدام الحاسوب العملاق:
و كان لخوارزمية برنت سالامن الاكتشاف الاروع والتي تبدأ بوضع:
ثم المعاودة:
حتى تصبح an وbn متقاربة بما يكفي. ويعطى تقريب π
في عام 2006 استطاع سيمون بلوف توليد سلسلة من الصيغ المدهشة بوضع q = eπ، وبالتالي
وأخرى بالشكل،
حيث q = eπ و k هو عدد فردي، وa, b, c هي أعداد نسبية. إذا كانت k على الشكل 4m + 3، تصبح الصيغة بالشكل المبسط،
صيغة بيلارد
حسّن منشورَ سيمون بلوف فابريس بيلارد مكتشفا صيغة حسابية جديدة أسرع بحوالي 43% من سابقتها كما أمكنه ولأول مرة بها حساب ط لرقم قياسي جديد على حاسوب شخصي لايتجاوز سعره 3000 دولار (وصل إلى 2.7 ترليون مرتبة عشرية مقارنة بالحساب السابق الذي تم بمساعدة الحاسوب العملاق للوصول إلى 2.6 ترليون مرتبة عشرية أو 1,000,000,000,000,000 مرتبة ثنائية) مع نهاية عام 2009. تدعى هذه الصيغة بصيغة بيلارد:
انظر أيضًا
المراجع
- ^ الثابت (ط) نسخة محفوظة 08 أكتوبر 2017 على موقع واي باك مشين.
- ^ Andrews، George E.؛ Askey، Richard؛ Roy، Ranjan (1999). Special Functions. مطبعة جامعة كامبريدج. ص. 58. ISBN:978-0-521-78988-2.
- ^ Gupta، R.C. (1992). "On the remainder term in the Madhava–Leibniz's series". Ganita Bharati. ج. 14 ع. 1–4: 68–71.
- ^ πe trillion digits of π نسخة محفوظة 6 December 2016 على موقع واي باك مشين.
- ^ Pi in the sky: Calculating a record-breaking 31.4 trillion digits of Archimedes’ constant on Google Cloud نسخة محفوظة 19 أكتوبر 2019 على موقع واي باك مشين.
- ^ Arndt & Haenel 2006، صفحة 17
- ^ Bailey، David؛ Borwein، Jonathan؛ Borwein، Peter؛ Plouffe، Simon (1997). "The Quest for Pi". The Mathematical Intelligencer. ج. 19 ع. 1: 50–56. CiteSeerX:10.1.1.138.7085. DOI:10.1007/bf03024340.
- ^ Holton، David؛ Mackridge، Peter (2004). "Greek: an Essential Grammar of the Modern Language". Routledge. ISBN:0-415-23210-4.
{{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب|دورية محكمة=(مساعدة), p. xi. - ^ "pi". Dictionary.reference.com. 2 مارس 1993. مؤرشف من الأصل في 2015-03-22. اطلع عليه بتاريخ 2012-06-18.
- ^ Arndt & Haenel 2006، صفحة 8
- ^ Apostol، Tom (1967). Calculus, volume 1 (ط. 2nd). Wiley.. p. 102: "From a logical point of view, this is unsatisfactory at the present stage because we have not yet discussed the concept of arc length." Arc length is introduced on p. 529.
- ^ Remmert، Reinhold (1991)، "What is π?"، Numbers، Springer، ص. 129
- ^ Richard J. Gillings (1972). Mathematics in the time of the Pharaohs. MIT press. ص. 124. مؤرشف من الأصل في 2022-04-11.
- ^ Arndt & Haenel 2006، صفحة 188. Newton quoted by Arndt.
- ^ BBC News - Pi calculated to 'record number' of digits نسخة محفوظة 11 مارس 2018 على موقع واي باك مشين.
- ^ موقع فابريس محطم الرقم العالمي للعام 2010 لحساب ط نسخة محفوظة 24 فبراير 2018 على موقع واي باك مشين.
- ^ Miller، Cole. "The Cosmological Constant" (PDF). جامعة ميريلاند (كوليج بارك). مؤرشف من الأصل (PDF) في 2018-10-24. اطلع عليه بتاريخ 2007-11-08.
- ^ Imamura، James M (17 أغسطس 2005). "Heisenberg Uncertainty Principle". جامعة أوريغون. مؤرشف من الأصل في 2008-12-20. اطلع عليه بتاريخ 2007-11-09.
- ^ Einstein، Albert (1916). "The Foundation of the General Theory of Relativity". Annalen der Physik. مؤرشف من الأصل (PDF) في 2012-02-06. اطلع عليه بتاريخ 2007-11-09.
- ^ Nave، C. Rod (28 يونيو 2005). "Coulomb's Constant". هايبرفيزيكس. جامعة ولاية جورجيا. مؤرشف من الأصل في 2019-04-13. اطلع عليه بتاريخ 2007-11-09.
- ^ "Magnetic constant". المعهد الوطني للمعايير والتقنية. 2006 لجنة بيانات العلوم والتقنية recommended values. مؤرشف من الأصل في 2 مايو 2019. اطلع عليه بتاريخ 2007-11-09.
{{استشهاد ويب}}: تحقق من التاريخ في:|تاريخ=(مساعدة) - ^ Weisstein، Eric W (7 أكتوبر 2004). "Gaussian Integral". موقع ماثوورلد. مؤرشف من الأصل في 2019-05-12. اطلع عليه بتاريخ 2007-11-08.
- ^ Weisstein، Eric W (11 أكتوبر 2005). "Cauchy Distribution". موقع ماثوورلد. مؤرشف من الأصل في 2019-05-02. اطلع عليه بتاريخ 2007-11-08.
وصلات خارجية
| في كومنز صور وملفات عن: ط |