|
تضامنًا مع حق الشعب الفلسطيني |
جداء نقطي
الجداء النقطي أو الضرب النقطي أو الجداء القياسي (بالإنجليزية: Dot product) ويسمى أحيانا الضرب القياسي أو الجداء السُلمي، هو عمليةٌ جبرية بين متجهين ونتيجتها كمية قياسية.
تعريف
تعريف جبري عام
ليكن فضاء متجهي حقيقي (معرف على حقل الأعداد الحقيقية )
نعرف الجداء السُلمي على أنه كل دالة :
تعريف على
الضرب القياسي الاعتيادي لمتجهتين و من يعرف ويرمز له بـ [1]
- على سبيل المثال، في الفضاء ثلاثي الأبعاد ، الضرب القياسي لمتجهين و هو :
تعريف هندسي
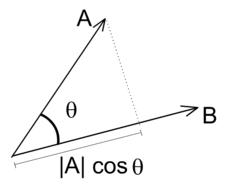
في الفضاء الإقليدي، صيغة أخرى لحاصل الضرب القياسي
حيث A هو طول المتجه A وB هو طول المتجه B وθ هي الزاوية المحصورة بينهما.
خصائص
- تبديلي :
- تنبثق هذه الخاصية من تعريف الجداء القياسي (θ هي الزاوية المحصورة بين a وb)
- توزيعي على جمع المتجهات : (a.b + a.c = a.(b+c
- تعامدي : متجهتان a وb مختلفتان عن الصفر يكونان متعامدتين إذا وفقط إذا توفر a.b = 0.
- لا إلغاء :
تطبيق لقانون الجيب التمام

وهذا هو قانون الجيب التمام. وتعبر أيضا عن خاصية الكاشي
في الفيزياء
الجداء القياسي يعبر عن كميات عددية لا علاقة لها برسم شعاع مثل (الجهد، العزم ....)
تعميمات
الجداء الداخلي
انظر إلى فضاء متجهي معياري.
انظر أيضا
مراجع
- ^ Seymour.، Lipschutz, (2009). Linear algebra (ط. 4th ed). New York: McGraw-Hill. ISBN:9780071543521. OCLC:192082884. مؤرشف من الأصل في 2010-01-12.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (مساعدة)صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link) صيانة الاستشهاد: علامات ترقيم زائدة (link)
وصلات خارجية
| في كومنز صور وملفات عن: جداء نقطي |