خط العالم

خط العالم (بالإنجليزية: World line)‏ لجسم ما «كالكواكب مثلا» هو وصف لمسار الجسم في الزمكان النسبي ذو الابعاد الاربعة (طول – عرض – ارتفاع) إضافة للبعد الرابع الزمن بتتبع تاريخ مسار الجسم  في الفضاء «يقصد بالفضاء الفضاء الكوني ولا يقصد به الفضاء الخارجي لكوكب الأرض مثلا» في كل لحظة زمنية، يعتبر مفهوم خط العالم من أهم المفاهيم  في الفيزياء الحديثة وبشكل خاص في الفيزياء النظرية.

يتميز مفهوم «خط العالم» عن مفاهيم أخرى مثل المدار الفلكي (كمدار كوكب في الفضاء) أو المسار (كمسار سيارة على الطريق) بأنه:

• يشمل بعد زمني.
• نموذجيا يحيط «يدرس» نطاقات واسعة من الزمكان حيث المسارات مباشرة «يمكن ان تعتبر مستقيمة» مراجعة حسابيا لتظهر نسبيتها بشكل مدرك أكثر لموضع مطلق لتكشف الطبيعة النسبية الخاصة وتأثر الجسم بالجاذبية

مثلا: سائق السيارة يقود في طريق مستقيم إلى الأمام أو الخلف «كلاهما يعتبر مسار مستقيم» عند مصادفته لمفترق طرق  فإنه يختار إحدى الجهتين وبمجرد اختياره لإحدى الجهتين فإن مساره يعتبر مستقيم بعد الانعطاف أما بالنسبة لمراقب مطلق «شخص ما يراقب السيارة من بعيد» فإن طبيعة المسار قد تكون مستقيمة أو منحنية.

ظهرت فكرة خط العالم على يد هيرمان مينكوفسكي ويستخدم المصطلح على نطاق واسع في النظرية النسبية لألبرت أينشتاين (مثل النسبية العامة والنسبية الخاصة).

الاستخدام في الفيزياء

في الفيزياء خط العالم لجسم ما يوصف كما النقطة في الفضاء (مثل الجسيم أو المراقب) هو متسلسلة من أحداث الزمكان تقابل تاريخ ذلك الجسم «أي كل ما طرأ على الجسم من تغيرات في تلك النقطة المعتبرة من الزمكان من بدايته وحتى اللحظة وإلى المستقبل» وخصوصا التغيرات في الجاذبية وبما أن كل جسم لديه كتلة خاصة به ويحني بها الزمكان والتي هي مولد الجاذبية حسب النسبية العامة فإن خط العالم يعتبر انحناء من نوع خاص في الزمكان تستعرض في التعريف الموجز التالي شرحا لمسألة اعتباره نوعا خاصا من انحناء الزمكان:

خط العالم يفسر كانحناء زمني في الزمكان. بمعنى أن لو شبهنا خط العالم  بمحور الأعداد الحقيقية  فأن كل نقطة من المحور تقابل حدثا يمكن أن يعنون مع  زمن حدوثه وموضعه الخاص  بالعنوان «الجسم في الوقت كذا»

مثلا مدار الارض في الفضاء تقريبا دائري الأبعاد الثلاث منحنية في الفضاء مع اعتبار الأرض تعود كل سنة إلى نفس النقطة  في الفضاء لكنها تصل هناك بتوقيت مختلف «وقت لاحق» عن وقت الوصول السابق  وتوضيحا للملاحظة 2 السابقة هنا موقع المراقب المطلق هو مركز الشمس فيكون خط العالم للأرض  أهليجي في الزمكان (الانحناء يكون في البعد الرابع للزمكان) وفي هذه الحالة فالأرض لا تعود ابدا إلى النقطة ذاتها.

الزمكان هو مجموع كل النقاط التي تدعى أحداث إضافة إلى نظام تحديد إحداثيات مستمر انسيابي لتمييز تلك الاحداث

كل حدث يمكن أن يعنون بواسطة أربع: إحداثية زمنية  وثلاث إحداثيات للفضاء معا يعطي الفضاء رباعي الابعاد «الزمكان»

خط العالم كأداة لوصف الأحداث

مستقيم ببعد وحيد أو انحناء يمكن أن يمثل كدالة إحداثية منسقة تتبع متحول وحيد «العامل المتغير» وكل قيمة للمتحول تقابل نقطة في الزمكان وتبين تفاوت أثر المتحول.

رياضيا الانحناء يعرف بأربع دوال إحداثية  «دالة هنا» حيث يمثل إحداثية الزمن عادة، اعتمادا على متحول وحيد

خط العالم في النسبية الخاصة

حتى اللحظة خط العالم (وكل مفاهيم الأشعة الظلية المرافقة) وصفت بدون أن تغطي بشكل ممنهج ومحدد المجالات بين الأحداث. التعبير الرياضي الأساسي للوصف كان: النظرية النسبية الخاصة وضعت بعض العراقيل والقيود لكل خط عالم  ممكن، ففي النسبية الخاصة وصف الزمكان لفضاء بنظام إحداثيات محدد، لا يراعي متسارع وغير قابل للتدوير أيضا تدعى نظم إحداثيات داخلية وفي مثل هذه النظم سرعة الضوء ثابتة وبنية الزمكان تحدد بثنائية η والتي بدورها تعطي أعداد حقيقية لكل زوج من الاحداث، صيغة الثنائية تسمى احيانا متر الزمكان «المتر كواحدة في الزمكان» ولكن طالما أن نتيجة الأحداث المميزة  أحيانا تعطي قيمة صفرية  على عكس متر الفضاء فصيغة الثنائية  لا تعتبر متر رياضي في الزمكان.

ثلاث خطوط عالم مختلفة تمثل التحرك تبعا لثابت زمني رابع يمثل بشعاع المحور t يمثل الزمن والمحور x يمثل المسافة لاحظ الفرق بالسرعة نتيجة إبطاء زمني ثقالي

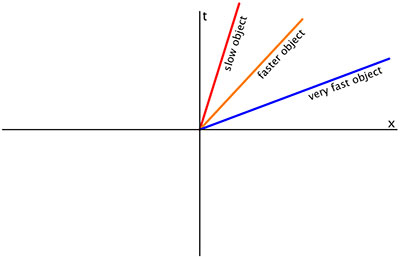
خطوط العالم للأجسام التي تخضع لسقوط حر تدعى جيوديزيا، في النسبية الخاصة تقابل خطوط مستقيمة في فضاء مينكوفيسكي.

عادة واحدات الزمن تكون تابعة لسرعة الضوء والذي يتم تمثيل كمستقيم بزاوية معينة، تكون عادة 45 درجة لتشكل مخروط مع محور الزمن (العمودي). بشكل عام، الانحناءات المفيدة في الزمكان تصنف إلى ثلاث أنماط  (الأنماط الأخرى قد تكون جزئيا من أحد الأنماط الثلاث وجزيئا من نمط آخر)

• الانحناءات المشابهة لمنحى الضوء light-like curves: وفي كل نقطة فيها النقاط لديها سرعة الضوء وتشكل مخروط في الزمكان مقسم إلى جزئين لمخروط له ثلاث أبعاد في الزمكان ويظهر كخط عند الرسم كقمع ببعدين وكمخروط عند الرسم  كقمع مكاني وحيد.
• الانحناءات المشابهة لمنحى لزمن time-like curves: لكل نقطة منها سرعة أقل من سرعة الضوء وهذه الانحناءات يجب

التزامن في المستو الفائق

بما أن خط العالم $w(\mathrm{\Im })\in \mathbb{R}4$تحدد تموضع وتسارع أي غرض بأربع اشعة $v=dwdr$ حيث $v=\frac{\mathrm{w}y}{{\tau }x}$من الانحناءات المشابهة لمنحى الزمن في الفضاء المينوفيسكي $\eta (v,x)$تحدد دالة جبرية $\mathbb{R}4⟶\mathbb{R}$بالصيغة $x⟶\eta (v,x)$

ليكن

$N$

بدالة جبر خطي لكيرنيل، تدعى

$N$

المحاكي الفائق بالنسبة لـ

$x$

، ونعرف نسبية التزامن بأنها مدى تغير

$N$

بتغير

$x$

مع العلم أن

$N$

مكمل التعامد لـ

$v$

بالنسبة ل

$\eta$

بينما يكون خطي العالم

$u,w$

نسبيان بالنسبة لـ

$dud\tau =dwd\tau$

فيكون

$\frac{\text{Not implemented MEDIAWIKIEXTENSIONMATHTEXVCNODESTEXNODE for operatorname}dw}{\mathrm{d}{\tau }}=\frac{dw}{d\tau }$

.

مثال على مخروط ضوئي، السطح الثلاثي الأبعاد لكل الاشعاعات الضوئية الممكنة الواصلة المبتعدة لنقطة في الزمكان، هنا تصور ارتباط البعد المكاني مع المخروط

عندها يتشاركان فئات تحاكي المستو الفائق، التحاكي الفائق موجود رياضيا، لكن العلاقات الفيزيائية في النسبية تتضمن حركة المعلومات بسرعة الضوء، وليس بشكل لحظي، فمثلا قانون كولوم الأساسي في الشحنات يمكن إسقاطه على مستو فائق ولكن العلاقات النسبية بين الشحنة والقوة المحركة تتضمن مواضع مختلفة عن قانون كولوم الكلاسيكي للقوة.

انظر أيضا

أنماط خاصة من خطوط العالم

• جيوديزيا

مواضيع مشابهة

• النسبية العامة
• الزمكان
• ألبرت أينشتاين
• هيرمان مينكوفسكي