ثقب أسود

من أرابيكا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
ثقب أسود

تعديل - تعديل مصدريحول القالب

الثقب الأسود الفائق "Powehi" داخل نواة المجرة الإهليلجية العملاقة أو السديم مسييه 78 التابع لكوكبة الجبار، تعود هذه الصورة لشبكة تلسكوب «ايفينت هوريزون»، وتظهر بقعة مظلمة أمام حلقة تضيء بشكل خافت، وعرضت لأول مرة خلال ستة مؤتمرات صحفية متزامنة تم إصداره في العاشر من أبريل لعام 2019
الثقب الأسود الفائق داخل نواة المجرة الإهليلجية العملاقة مسييه 87 التابعة لكوكبة العذراء. تعدّ هذه الصورة أول صورة حقيقية لثقب أسود، وتعود لشبكة مقراب أفق الحدث، وتظهر فيها بقعة مظلمة أمام حلقة تضيء بشكل خافت، وعُرضت لأول مرة خلال ستة مؤتمرات صحفية متزامنة تمت في العاشر من أبريل عام 2019.
جزء من سلسلة مقالات حول
النسبية العامة
Spacetime curvature schematic
Gμν+Λgμν=8πGc4Tμν
المفاهيم الأساسية
الظواهر
زمكان
  • المعادلات
  • الشكليات
المعادلات
الشكليات
نظريات متقدمة
الحلول
علماء
شعار بوابة بوابة الفيزياء

الثقب الأسود هو منطقة موجودة في الزمكان (الفضاء بأبعاده الأربعة، وهي الأبعاد الثلاثة بالإضافة إلى الزمن) تتميز بجاذبية قوية جداً بحيث لا يمكن لأي شيء - ولا حتى الجسيمات أو موجات الإشعاع الكهرومغناطيسي مثل الضوء - الإفلات منها.[1] تتنبأ النظرية النسبية العامة بأنه يمكن لكتلة فائقة الضخامة أن تنضغط بقدر معين بحيث تشوه الزمكان وتشكيل ثقب أسود.[2][3] يُطلق على حدود المنطقة التي لا يُمكن الهروب منها اسم أفق الحدث. وعلى الرغم من أن عبور حدود أفق الحدث له تأثيرات هائلة على مصير وظروف أي جسم يعبُره، إلا أنه لا تظهر أي خصائص يُمكن مشاهدتها لهذه المنطقة، فالضوء لا يمكن أن يفلت منها.[4] يعمل الثقب الأسود بصفته جسما أسودا مثاليا، لأنه لا يعكس ولا يٌصدر أي ضوء أو اي شيء آخر.[5][6] علاوة على ذلك، تتنبأ نظرية المجال الكمي في الزمكان المنحني ‏ بإمكانية إنبعاث إشعاع هوكينج من أفق الحدث، بنفس الطيف الذي يتسم به الجسم الأسود لدرجة حرارة تتناسب عكسياً مع كتلته. درجة الحرارة هذه منخفضة جدا جدا فهي في حدود جزء من مليار الكلفن . كما توجد ثقوب سوداء ذوي كتلة نجمية، ومع ذلك فهي أيضا لا يمكن مشاهدتها. يمكن معرفة وجودها من خلال تأثيراتها على محيطه بيئتها.

أشار كل من جون ميشيل وبيير سيمون لابلاس إلى وجود أجسام تمتلك حقول جاذبية قوية بحيث لا يمكن للضوء أن يهرب منها في القرن الثامن عشر.[7] عثر كارل شوارزشيلد على أول حل رياضي حديث للنسبية العامة التي تُميز الثقب الأسود في عام 1916، إلا أن تفسير الحل الرياضي شَكّل منطقة فضاء لا يمكن أن يفلت منها أي شيء كان قد نشر لأول مرة من قِبل ديفيد فينكلشتاين في عام 1958. كانت الثقوب السوداء تعتبر مجرد خيال وفضول لدى علماء الرياضيات لفترة طويلة. لكن خلال ستينيات القرن العشرين، أظهر العمل النظري تنبؤ النسبية العامة بالثقوب. أثار اكتشاف نجوم نيوترونية بواسطة جوسلين بيل بورنيل في عام 1967 الاهتمام بالأجسام المدمجة المنهارة بالجاذبية بصفتها حقيقة فيزيائية فلكية ممكنة.

يُعتقد أن الثقوب السوداء ذات الكتلة النجمية تتشكل عند انهيار النجوم الضخمة جدًا في نهاية دورة حياتها. بعد أن يتشكل الثقب الأسود، يمكن أن يستمر في النمو عن طريق امتصاص الكتلة من محيطه. وذلك عن طريق امتصاص النجوم الأخرى والاندماج مع الثقوب السوداء الأخرى، الأمر الذي قد يؤدي إلى تشكل الثقوب السوداء الهائلة والتي تحمل كتلة تعادل ملايين الكتل الشمسية (M ☉). هناك إجماع عام على وجود ثقوب سوداء هائلة في مراكز معظم المجرات.

على الرغم من أن محتواه غير مرئي، يمكن استنتاج وجود ثقب أسود من خلال تأثيره على المواد الأخرى والإشعاع الكهرومغناطيسي مثل الضوء المرئي. يمكن للمادة التي تسقط في الثقب الأسود أن تُشكّل قرص تراكم خارجي يتم تسخينه عن طريق الاحتكاك، مما يؤدي إلى تشكيل بعضٍ من أشد الأجسام بريقا في الكون. إذا كان هناك نجوم أخرى تدور حول ثقب أسود، فيمكن استخدام كل من مداراتها وكتلتها لتحديد كتلة الثقب الأسود وموقعه. يمكن استخدام هذه الملاحظات لاستبعاد البدائل المحتملة مثل النجوم النيوترونية. وبهذه الطريقة، تحقق علماء الفلك من العديد من حالات توقعات وجود الثقب الأسود النجمي ضمن الأنظمة الثنائية، وأثبتوا أن مصدر الراديو المعروف بٱسم الرامي A، في قلب مجرة درب التبانة، يحتوي على ثقب أسود هائل يحمل كتلة تقارب 4.3 مليون كتلة شمسية.

في 11 فبراير 2016، أعلن تحالف مرصد ليغو عن أول اكتشاف مباشر لموجات الجاذبية، والتي تعكس فكرة العثور على لحظة اندماج الثقوب السوداء.[8] اعتبارًا من ديسمبر 2018، عُثر على إحدى عشرة موجة من موجات الجاذبية التي نشأت من اندماج عشرة ثقوب سوداء وموجة جاذبية واحدة ناتجة عن اندماج نجم نيوتروني ثنائي.[9][10] في 10 أبريل 2019، تم نشر أول صورة على الإطلاق لثقب أسود وما في جواره، وذلك في أعقاب القراءات التي حصل عليها مقراب أفق الحدث في عام 2017 والمتعلقة بالثقب الأسود الهائل في مركز المجرة مسييه 87.[11][12]

التاريخ

عرض محاكاة لثقب أسود أمام سحابة ماجلان الكبرى. لاحظ تأثير عدسة الجاذبية، الذي يُنتج منظرين مكبرين ولكن مشوهين للغاية للسحابة. ويظهر شكل قرص درب التبانة، عبر الجزء العلوي، مشوهًا على شكل قوس.

اقترح الفلكي ورجل الدين الإنجليزي جون ميشيل تصوره لوجود جسم ضخم جدا لدرجة أنه لا يسمح للضوء بأن يفلت منه، وذلك في بحث نشره في نوفمبر 1784. افترضت حسابات ميشيل أن مثل هذا الجسم قد يملك نفس كثافة الشمس، وخَلُص إلى أن مثل هذا الجسم سوف يتشكل عندما يتجاوز قطر النجم قطر الشمس بـ 500 مرة، محتسبا أن سرعة الهروب من سطحه ستتجاوز سرعة الضوء المعتادة. أشار ميشيل إلى أنه يمكن اكتشاف هذه الأجسام الفائقة الحجم ولكن غير المرئية من خلال آثارها الجاذبية على الأجسام المرئية القريبة.[7][13][14] كان الباحثون في ذلك الوقت متحمسين للاقتراح القائل بأن هنالك نجوم عملاقة ولكن غير مرئية أمام أنظارهم، ولكن ذلك الحماس تضاءل عندما أصبحت الطبيعة الموجية للضوء معروفة في أوائل القرن التاسع عشر.[15] فأصبح الطرح وقتها أن الضوء موجة وليس «جسما»، وعليه فتأثير الجاذبية على الموجات لن يقاس بنفس أسلوب القياس المتبع على الجسيمات، هذا إن وُجد تأثير للجاذبية على الأمواج الضوئية.[7][14] النسبية الحديثة خطأت تصور ميشيل لإمكانية انطلاق شعاع ضوئي، مرتفعا من سطح نجم ضخم، ويبدأ بالتباطؤ بسبب جاذبية النجم، ويتوقف بعدها، ثم يسقط مرة أخرى على سطح النجم وكأنه كرة.[16]

النسبية العامة

في عام 1915، طور ألبرت أينشتاين نظريته النسبية العامة، حيث كان قد أثبت في وقت سابق أن الجاذبية تؤثر على حركة الضوء. بعد ذلك ببضعة أشهر فقط، وجد كارل شوارزشيلد حلاً لمعادلات آينشتاين للمجال، والتي تصف مجال الجاذبية لكل من الكتلة النقطية والكتلة الكروية.[17] بعد بضعة أشهر من نتائج شوارزشيلد، قدم يوهانس دروست، وهو من طلبة هندريك لورنتز، الحل نفسه، وبشكل مستقل عن عمل شوارزشيلد، لوصف النقطة ذات الكتلة وكتب متعمقا بتفصيل أفضل وأوسع عن خصائصها.[18][19] ظهر ضمن نتائج وحلول يوهانس نتيجة، تعرف في الوقت الحاضر بٱسم نصف قطر شوارزشيلد، حيث تؤول النقطة إلى وضعية التفرد، مما يعني أن بعض المتغيرات ضمن معادلات آينشتاين أصبحت بقيم لا نهائية. لم تكن طبيعة هذا الأمر مفهومة تمامًا في ذلك الوقت. في عام 1924، أثبت آرثر إدينجتون أن التفرد يختفي بعد تغيير الإحداثيات (انظر إحداثيات إدينجتون-فينكلشتاين ‏)، إلا أن الأمر استغرق حتى عام 1933 حتى أدرك جورج ليمايتر أن هذا يعني أن التفرد في دائرة نصف قطرها مقدار شوارزشيلد هو تفرد في الإحداثيات ‏ غير المادية.[20] كتب آرثر إدينغتون معلقا على احتمال وجود نجم ذي كتلة مضغوطة لحجم نصف قطر شوارزشيلد في كتاب صدر عام 1926، مشيرًا إلى أن نظرية أينشتاين تسمح لنا باستبعاد الكثافات المرتفعة جداً ضمن النجوم المرئية مثل منكب الجوزاء لأن

«نجما يبلغ قطره 250 مليون كيلومتر لا يمكنه أن يملك كثافة مرتفعة مثل تلك الموجودة لدى الشمس. أولاً، ستكون قوة الجاذبية كبيرة لدرجة أن الضوء لن يكون قادرًا على الهروب منه، ستسقط الأشعة إليه ثانية كسقوط الحجر عائدا إلى الأرض. ثانياً، سيكون الانزياح نحو الأحمر كبيراً لدرجة أنه سيتم إزاحة الطيف خارج الوجود. ثالثًا، ستنتج الكتلة انحناءًا كبيرًا في مقياس الزمان والمكان بحيث يتم إغلاق الفضاء حول النجم، مما سيتركنا في الخارج (أي، في أي مكان)».[21][22]

في عام 1931، توصل سوبرامانيان تشاندراسيخار، مستخدما النسبية الخاصة، إلى أن جسما لا يدور ومكونا من المادة المنحلة للإلكترون وبكتلة أعلى من قيمة محددة (تسمى الآن حد تشاندراسيخار 1.4 M☉) لن يمتلك حلولا مستقرة ضمن النسبية.[23] تم معارضة استنتاجاته من قبل الكثير من معاصريه مثل إدينغتون وليف لانداو، الذين ردوا عليه أنه لا بد من وجود آليات غير معروفة ستوقف انهيار المادة.[24] حملت معارضاتهم بعضا من الصحة: فالقزم الأبيض الأكبر قليلاً من حد تشاندراسيخار ينهار ليصبح نجمًا نيوترونيًا، [25] وهو جسم مستقر بحد ذاته. لكن في عام 1939، توقع روبرت أوبنهايمر وآخرون أن النجوم النيوترونية فوق حد آخر (حد تولمان - أوبنهايمر - فولكوف) ستنهار بناء على التعليلات التي قدّمها تشاندراسيخار، وخَلَصوا إلى أنه من غير المحتمل أن يوجد أي قانون فيزيائي يمكنه أن يوقف انهيار بعض النجوم مما يعني تحولها إلى ثقوب سوداء.[26] حساباتهم الأصلية، المبنية على مبدأ استبعاد باولي، حددت قيمة الحد الجديد بـ 0.7 M☉؛ الفهم اللاحق للقوة المرتفعة التي تؤثر على تنافر النجوم النيوترونية رفعت التقدير إلى قيم تتراوح ما بين 1.5 M☉ إلى 3.0 M☉.[27] أدت القراءات التي تم تسجيلها في مرصد ليغو للموجة الثقالية الناتجة عن اندماج النجم النيوتروني GW170817، والذي يُعتقد أنه أدى إلى ظهور ثقب أسود بعد ذلك بفترة قصيرة، إلى تحسين تقدير حد تولمان - أوبنهايمر - فولكوف إلى 2.17 M☉.[28][29][30][31][32]

فسر أوبنهايمر وزملاؤه التفرد على حدود دائرة نصف قطرها قيمة شوارزشيلد على أنه مؤشر على أن هذه هي حدود الفقاعة التي يتوقف الوقت داخلها. وجهة نظر مناسبة للمراقبين خارج الفقاعة، ولكنها بالتأكيد ليست ما يلاحظه الجسم الساقط داخل الفقاعة. وبسبب هذه الخاصية، كانت النجوم المنهارة تسمى «النجوم المجمدة»، لأن المراقب الخارجي سيرى سطح النجم متجمدًا في اللحظة التي يصل بها حجم الانهيار إلى نصف قطر شوارزشيلد.[33]

العصر الذهبي

في عام 1958، أقر ديفيد فينكلشتاين بأن سطح شوارزشيلد هو أفق للحدث، «غشاء مثالي أحادي الاتجاه: يمكن للتأثيرات السببية أن تعبره ولكن في اتجاه واحد فقط».[34] لم يتعارض هذا بشكل صارخ مع نتائج أوبنهايمر، لكنه وسع مفاهيمها لتشمل وجهة نظر الأجسام التي تجاوزت أفق الحدث. حل فنكلشتاين ‏ سمح لحل شوارزشيلد بالارتباط بمستقبل الأجسام التي سقطت في ثقب أسود. واستطاع مارتن كروسكال العثور على حل كامل ‏ وقام بنشره سريعا.[35]

جاءت هذه النتائج في بداية العصر الذهبي للنسبية العامة، الذي تميز بسيادة قضايا النسبية العامة والثقوب السوداء مواضيعا رئيسة للبحث العلمي. ساعد على ذلك اكتشاف النجوم النابضة بواسطة جوسلين بيل بورنيل في عام 1967، [36][37] والتي، بحلول عام 1969، تبين أنها نجوم نيوترونية تدور بسرعات عالية جدا.[38] حتى ذلك الوقت، كان ينظر إلى النجوم النيوترونية، مثلها مثل الثقوب السوداء، على أنها مجرد شطحات وترف فكري نظري؛ لكن اكتشاف النجوم النابضة أوضح أهميتها الفيزيائية وأثار اهتمامًا إضافيًا بجميع أنواع الأجسام المنهارة بسبب الجاذبية.

في هذه الفترة تم العثور على حلول رياضية أكثر عمومية للثقوب السوداء. في عام 1963، وجد روي كير الحل الدقيق لمسألة الثقب الأسود الدوار. بعد ذلك بعامين، وجد عزرا تي نيومان الحل الرياضي لمحاكاة ثقب أسود متناظر المحاور يدور ومشحون كهربائياً.[39] من خلال عمل فيرنر إسرائيل، [40] براندون كارتر، [41][42] وديفيد روبنسون [43] ظهرت نظرية اللاشعر (No-Hair Theorem) ‏، والتي تنص على أن الثقب الأسود الثابت يمكن وصفه تماما من خلال ثلاثة خصائص فقط، قياسات كير-نيومان ‏: الكتلة، الزخم الزاوي، والشحنة الكهربائية.[44]

في البداية، كان يعتقد أن السمات الغريبة التي تظهر في الحلول الرياضية لنماذج الثقب الأسود كانت عبارة عن نتائج متطرفة بسبب افتراض شرط التناظر ضمن النماذج الرياضية، وعليه فهذه النتائج الفردية لا يجب أن تظهر في الحلول الرياضية التي تشرح النماذج العامة. تم هذا الرأي بشكل خاص من قِبل وإسحاق خلاتنيكوف وإفغيني ليفشيتز، الذين حاولوا إثبات انعدام ظهور التفرد في الحلول الرياضية العمومية. إلا أن روجر بنروز [45] وستيفن هوكينج، في أواخر الستينيات، أثبتا أن الخصائص الفردية تظهر فعلا ضمن الحلول الرياضية العمومية.[46]

أدى عمل كل من جيمس باردين وجاكوب بيكينشتاين وكارتر وهوكينج في أوائل سبعينيات القرن الماضي إلى صياغة قوانين الديناميكا الحرارية للثقب الأسود.[47] تصف تلك القوانين سلوك الثقب الأسود بشكل متفق مع قوانين الديناميكا الحرارية وذلك من خلال ربط الكتلة مع الطاقة، والمساحة مع الانتروبيا، والجاذبية السطحية مع درجة الحرارة. تكاملت الفكرة عندما توصل هوكينج، في عام 1974، إلى أن نظرية المجال الكمي تتنبؤ بأن الثقوب السوداء يجب أن تشع مثلها مثل الجسم الأسود عند درجة حرارة تتناسب مع الجاذبية السطحية للثقب الأسود.[48]

أصل المصطلحات المستعملة

استخدم جون ميشيل مصطلح «النجم المظلم»، [49] وفي أوائل القرن العشرين، استخدم الفيزيائيون مصطلح «الجسم المنهار الثقالي». تتبعت كاتبة العلوم مارسيا بارتوسياك مصطلح «الثقب الأسود» للفيزيائي روبرت هـ. ديكي ‏، الذي قيل أنه قارن في أوائل الستينيات من القرن الماضي هذه الظاهرة بالثقب الأسود في كلكتا؛ سجن مشهور يدخله الناس أحياء ويخرجون منه أمواتا.[50]

وقد تم استخدام مصطلح «الثقب الأسود» في المجلات ضمن مجلتي الحياة وأخبار العلوم عام 1963، [50] وأيضا استعملتها الصحافية آن يوينغ في مقالها «الثقوب السوداء في الفضاء»، بتاريخ 18 يناير عام 1964، حيث كتبت تقريرا عن اجتماع للرابطة الأمريكية لتقدم العلوم في كليفلاند، أوهايو.[51][52]

يُقال أن أحد الطلاب أثناء محاضرة لجون ويلر في ديسمبر 1967 اقترح عبارة «الثقب الأسود»؛ [51] تبنى ويلر المصطلح، وسرعان ما انتشر استعماله، [53] مما دفع البعض إلى إعطاء الفضل لويلر على صياغة العبارة.[54]

الخصائص والتركيب

رسم توضيحي بسيط لثقب أسود لا يدور

تفترض نظرية اللا شعر ‏، أنه بمجرد وصول الثقب الأسود لحالة مستقرة بعد تكونه، تصبح له، فقط، ثلاث خصائص فيزيائية مستقلة: الكتلة، الشحنة، والزخم الزاوي. وبخلاف ذلك فالثقب الأسود لا يحمل أي خصائص أخرى. إذا كانت الفرضية سليمة، فهذا سيعني استحالة تمييز أي من الثقوب السوداء التي تشترك بنفس القيم لهذه الخصائص عن بعضها البعض. إن درجة مطابقة النظرية مع الثقوب السوداء على أرض الواقع ووفقًا لقوانين الفيزياء الحديثة، هي مشكلة لم يتم حلها بعد.[44]

هذه الخصائص خاصة لأنها مرئية من خارج الثقب الأسود. على سبيل المثال، فإن الثقب الأسود المشحون سيتنافر مع الشحنات التي تشبه شحنته مثله مثل أي جسم مشحون آخر. وبالمثل، يمكن العثور على الكتلة الكلية لكرة تحوي ثقبا أسود باستخدام التناظرية الجاذبية لقانون جاوس، كتلة إي دي إم ‏، وذلك بعيدًا عن الثقب الأسود.[55][بحاجة لتوضيح] وبالمثل، يمكن قياس الزخم الزاوي من بعيد باستخدام سحب الإطار بواسطة مجال مغناطيسية الجاذبية.[بحاجة لتوضيح]

عندما يسقط جسم في ثقب أسود، يتم توزيع المعلومات المرتبطة «بشكله أو توزيع الشحنة عليه» بالتساوي على طول أفق الثقب الأسود، ويتم فقد أثرها من قبل أي مراقب من الخارج. إن سلوك الأفق في هذه الحالة يمكن تفسيره على أنه نظام تبديد ‏ بسلوك يشابه، إلى حد بعيد، سلوك غشاء قابل للتمدد له مقاومة لكل من الاحتكاك وللتوصيل الكهربائي - نموذج الغشاء ‏.[56] هذا يختلف عن نظريات المجال الأخرى مثل الكهرومغناطيسية، التي لا تحتوي على أي احتكاك أو مقاومة على المستوى المجهري، لأنها قابلة للانعكاس ضمن الوقت ‏. ونظرًا لأن الثقب الأسود يصل في النهاية إلى حالة مستقرة مع ثلاثة خصائص فقط، فهذا يعني أنه لا توجد طريقة لتجنب فقدان المعلومات التي وصلته: تُوفر حقول الجاذبية والكهرباء في الثقب الأسود معلومات قليلة جدًا عن الأجسام التي تعبر إلى الداخل. تتضمن المعلومات المفقودة كل كمية لا يمكن قياسها بعيدًا عن أفق الثقب الأسود، بما في ذلك أرقام الكم المحفوظة تقريبًا مثل العدد الإجالي لباريون ورقم اللبتون. هذا السلوك محير جدا لدرجة أنه أخذ تسميته مفارقة فقدان معلومات الثقب الأسود.[57][58]

تمدد وقت الجاذبية حول ثقب أسود

الخصائص الفيزيائية

أبسط الثقوب السوداء الساكنة هي ثقوب بكتلة ولكنها لا تحمل شحنة كهربائية ولا زخم زاوي لها. غالباً ما يشار إلى هذه الثقوب السوداء باسم ثقوب شوارزشيلد السوداء وذلك تقديراً لكارل شوارزشيلد الذي اكتشف هذا الحل الرياضي ‏ عام 1916.[17] وفقًا لنظرية بيرخوف ‏، فذلك هو الحل الفراغي الوحيد المتناظر كرويًا ‏.[59] هذا يعني أنه لا يوجد فرق ملحوظ بين مجال الجاذبية لهذا الثقب الأسود وأي مجال كروي آخر يحمل نفس الكتلة. وبالتالي فإن الفكرة الشائعة عن «امتصاص الثقب الأسود لكل شيء» هي فقط صحيحة ضمن محيط الثقب الأسود بالقرب من أفقه؛ أما بعيدًا، فإن حقل الجاذبية الخارجي مطابق لحقل أي جسم آخر، له نفس الكتلة.[60]

توجد حلول تصف الثقوب السوداء العامة. يتم وصف الثقوب السوداء المشحونة غير الدوارة بواسطة مقياس رايسنر-نوردستروم، في المقابل يصف مقياس كير الثقب الأسود الدوار وغير المشحون. الحل المعروف للثقب الأسود الثابت هو مقياس كير-نيومان ‏، والذي يصف ثقباً أسود يحمل شحنة وزخماً زاوياً.[61]

وفي حين أن كتلة الثقب الأسود يمكن أن تأخذ أي قيمة موجبة، فإن الشحنة والزخم الزاوي مقيدان بالكتلة. في وحدات بلانك، الشحنة الكهربائية الكلية Q والزخم الزاوي الكلي J عليهما أن يتبعا القاعدة

Q2+(JM)2≤M2

وذلك ضمن ثقب أسود له كتلة بمقدار M. وتسمى الثقوب السوداء التي تملك الحد الأدنى من الكتلة اللازمة لتلبية هذا التباين بالثقوب السوداء المتطرفة ‏. توجد حلول لمعادلات آينشتاين، تنتهك معادلة عدم المساواة هذه، لكنها لا تقدم أفقًا للحدث. تقدم هذه الحلول الرياضية ما يسمى بنقاط التفرد المجردة، وهي نقاط تفرد يمكن للمراقب من الخارج رؤيتها لإنعدام الأفق حولها، وعليه فقد اعتبرت حلولا رياضية غير ملائمة للواقع الفيزيائي للكون. تستبعد فرضية الرقابة الكونية تشكيل مثل هذه التفردات، من خلال الانهيار الجاذبي للمادة الحقيقية ‏.[2] تم دعم هذا الادعاء من خلال المحاكاة العددية.[62]

بسبب القوة الكبيرة نسبيا للقوة الكهرومغناطيسية، فمن المتوقع احتفاظ الثقوب السوداء المتكونة من انهيار النجوم بكامل الشحنة المحايدة (تقريبًا) للنجم. الدوران، في المقابل، هو ميزة متوقعة للأجسام الفلكية الفيزيائية المنضغطة. الثقب الأسود (المرشح) GRS 1915 + 105 [63] لديه قوة دفع زاوي قريبة من الحد الأقصى للقيمة المسموحة. هذا الحد غير المشحون هو [64]

J≤GM2c,

مما يسمح بتعريف معامل الدوران بدون أبعاد على الشكل:[64]

0≤cJGM2≤1.[65][Note 1]

تصنيف الثقوب السوداء
صنف الكتلة التقديرة نصف القطر القديري
ثقب أسود عملاق 10 5 -10 10 MSun 0.001–400 AU
ثقب أسود متوسط الكتلة 10 3 م Sun 10 3 كم ≈ R Earth
ثقب أسود نجمي 10 م Sun 30   كم
الثقب الأسود الصغير حتى Mالقمر حتى 0.1   مم

تصنف الثقوب السوداء عادة حسب كتلتها، بدون الإعتماد على زخمها الزاوي، J. يتناسب حجم الثقب الأسود، كما يحدده نصف قطر أفق الحدث، أو نصف قطر شوارزشيلد، مع الكتلة، M ، من خلال المعادلة

rs=2GMc2≈2.95MMSunkm,

حيث rs هي نصف قطر شفارتزشيلد و MSun هي كتلة الشمس.[1] بالنسبة إلى الثقب الأسود الذي يحمل قيم لا صفرية لكل من الدوران والشحنة، يكون نصف القطر أصغر،[Note 2] بحيث يتمكن الثقب الأسود المتطرف ‏ من الحصول على أفق حدث قريب جدا.[67]

أفق الحدث

بعيدا عن الثقب الأسود ، يمكن للجسيم أن يتحرك في أي اتجاه ، كما يتضح من مجموعة الأسهم. لكن حركته تقتصر على حدود سرعة الضوء.
مع الأقتراب أكثر إلى الثقب الأسود، يبدأ الزمكان بالتشوه. و تصبح هناك المسارات متجهة نحو الثقب الأسود أكثر من نلك المسارات التي تتحرك بعيدًا.[Note 3]
داخل أفق الحدث ، جميع المسارات تنقل الجسيم قريبا إلى مركز الثقب الأسود. تنعدم إمكانية هروب الجسيم.

السمة المميزة للثقب الأسود هي ظهور أفق الحدث - وهو الحدود ضمن الزمكان والتي من خلالها يمكن للمادة والضوء المرور فقط إلى الداخل نحو كتلة الثقب الأسود. لا شيء، ولا حتى الضوء، يمكنه الإفلات من داخل أفق الحدث. يشار إلى استعمال عبارة «أفق الحدث» على هذا النحو لأنه وفي حالة حدوث حدث ما داخل حدوده، فإنه من المستحيل للمعلومات الناتجة عن هذا الحدث أن تصل إلى مراقب خارج تلك الحدود، مما يجعل من المستحيل التعرف على حدوث حدث من ذاك القبيل.[69]

كما تنبأت النسبية العامة، فإن وجود جسم بكتلة يحدث تشوهاً بالزمكان بحيث تنحرف المسارات التي تتخذها الجزيئات نحو الكتلة.[55] في أفق الحدث لثقب أسود، يصبح هذا التشوه قويًا جدًا بحيث لا توجد مسارات تؤدي بعديا عن الثقب الأسود.[70]

بالنسبة للمراقب البعيد، ستظهر نبضات الساعات القريبة من الثقب الأسود أكثر بطئاً من الساعات البعيدة عن الثقب الأسود.[55] نتيجة لهذا التأثير، والمعروف باسم تمدد وقت الجاذبي، سيبدو أن الجسم الذي يسقط في ثقب أسود يتباطأ كلما اقترب من أفق الحدث، وسيستغرق وقتًا لا نهائيا للوصول إليه.[55] في الوقت نفسه، تتباطأ جميع العمليات على هذا الجسم، من وجهة نظر مراقب خارجي ثابت، مما يؤدي إلى ظهور أي ضوء منبعث من الجسم بشكل أغمق وأكثر احمراراً، وهو تأثير يُعرف باسم الانزياح نحو الأحمر التثاقلي.[71] في النهاية، يتلاشى الجسم الساقط حتى لا يعود بالإمكان رؤيته. عادةً ما تحدث هذه العملية بسرعة كبيرة عند اختفاء الجسم وخلال أقل من ثانية.[72]

من ناحية أخرى، لا يلاحظ المراقب، الغير قابل للتدمير، أثناء عبوره لأفق الحدث إلى داخل الثقب الأسود أيًا من هذه الآثار. فوفقًا لساعاته الخاصة، والتي تبدو له أنها تعمل بشكل طبيعي، هو سيعبر أفق الحدث بعد فترة زمنية محدودة دون ملاحظة إلى أي معالم دالة على وجود تفرد، في النسبية العامة الكلاسيكية، من المستحيل تحديد موقع أفق الحدث اعتمادا على الملاحظات المحلية، بسبب مبدأ التكافؤ لآينشتاين.[55][73]

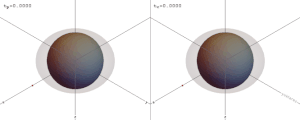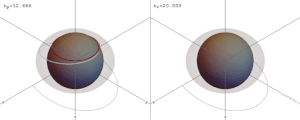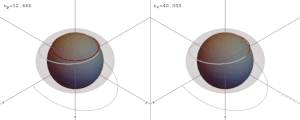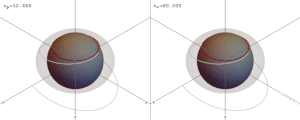
شكل أفق الحدث حول الثقب الأسود قريب جداً من الكروية.[Note 4][76] بالنسبة للثقوب السوداء التي لا تدور (الثابتة)، يكون أفق الحدث كرويا تمامًا، بينما بالنسبة لأفق الثقوب السوداء التي تدور، يكون أفق الحدث ملتزمًا بالشكل الكروي.[77]

التفرد

في وسط الثقب الأسود، كما هو مطروح في النسبية العامة، يقبع تفرد جذبوي، وهي المنطقة التي يصبح ضمنها انحناء الزمكان لانهائياً.[55] بالنسبة لثقب أسود غير دوراني، تتخذ هذه المنطقة شكل نقطة واحدة، أما بالنسبة لثقب أسود دوار، فيتم تشويه المنطقة لتشكل تفرد حلقي يقع في مستوى الدوران.[55] في كلتا الحالتين، سيكون لمنطقة التفرد حجم صفري. يمكن أيضًا إثبات أن منطقة التفرد تحتوي على كامل كتلة الثقب الأسود.[55] وبالتالي يمكن اعتبار منطقة التفرد مجرد نقطة لكنها ذات كثافة لا حصر لها.[78]

لا يمكن للمراقب الذي يسقط في ثقب شوارزشيلد الأسود ( غير متناوب وغير مشحون) أن يتجنب وصوله إلى نقطة التفرد بمجرد عبوره لأفق الحدث. يمكنه إطالة وجوده من خلال تسارعه بعيداً عن نقطة التفرد لإبطاء سرعة نزوله، ولكن فقط إلى حد معين.[79] عندما يصل إلى نقطة التفرد، سيتم سحقه إلى كثافة لا حصر لها وتضاف كتلته إلى إجمالي كتلة الثقب الأسود. ولكن قبل أن يحدث ذلك، سيكون جسمه قد تمزق بسبب قوى المد والجزر المتنامية في عملية يشار إليها باسم تأثير المعكرونة.[80]

في حالة وجود ثقب أسود مشحون (ثقب رايسنر-نوردستروم) أو ثقب كبير أسود، يمكن تجنب التفرد. دفع قيم الحلول الرياضية إلى حدها الأقصى يكشف عن إمكانية افتراضية للخروج من الثقب الأسود ولكن إلى زمكانٍ مختلف، حيث يعمل الثقب الأسود كثقب دودي.[55] طبعاً تبقى إمكانية السفر إلى كون آخر مجرد خيال علمي كون الاضطراب الحادث ضمن الثقب سيدمر احتمال حدوث ذلك.[81] الحلول الرياضية المختلفة تعطي انطباعا بإمكانية اتباع منحنيات توقيت مغلقة ‏ حول نقطة تفرد كير، مما قد يُفسر على أنه عودة إلى ماضي الشخص، مما سيؤدي إلى مشاكل ومفارقات مع مبدأ السببية مثل مفارقة الجد.[55] من المتوقع ألا تنجو المادة التي تُشكل الإجسام التي تسقط في الثقوب من الإضرابات الكيمومية الغريبة ضمن هذه الثقوب السوداء الدوارة والمشحونة.[82]

عادة ما يُنظر إلى ظهور التفرد في النسبية العامة على أنه إشارة إلى انهيار النظرية.[1] إلا أن هذا الانهيار أمر متوقع عندما تؤدي التأثيرات الكمية إلى حدوث هذا الإنهيار بسبب الكثافة العالية للغاية وبالتالي تفاعل الجسيمات الكمية. حتى الآن، لم يكن من الممكن الجمع بين الآثار الكمومية والجاذبية في نظرية واحدة، على الرغم من وجود محاولات مضنية لصياغة مثل هذه النظرية للجاذبية الكمية. بشكل عام، من المتوقع ألا تتضمن هذه النظرية وجود أي تفرد.[83][84]

محيط الفوتون

محيط الفوتون أو كرة الفوتون هي حدود كروية بسماكة صفرية يتم ضمنها التقاط وحبس الفوتونات التي تتحرك بشكل ملامس لمماسها ضمن مدار دائري حول الثقب الأسود. بالنسبة إلى الثقوب السوداء غير الدوارة، فإن كرة الفوتون لها دائرة نصف قطرها 1.5 مرة نصف قطر شوارزشيلد. مدارات الفوتونات غير مستقرة ديناميكيًا ‏، وبالتالي فإن أي اضطراب صغير يتسبب به أي جسيم مادي من شأنه أن يتسبب في عدم استقرار ينمو مع الوقت، و بالتالي ينتقل الفوتون إلى مسار خارجي يؤدي إلى هربه من الثقب الأسود، أو مسار للداخل حيث سيعبر أفق الحدث.[85]

وبينما لا يزال بالإمكان للضوء الإفلات من كرة الفوتون، فإن الثقب الأسود سوف يلتقط أي ضوء يعبر كرة الفوتون ضمن مسار له اتجاه داخلي. وأي إضاءة تصل إلى مراقب خارج كرة الفوتون هي إضاءة صادرة عن أجسام تقع بين كرة الفوتون وأفق الحدث.[85]

إرغوسفير

إيرجوسفير هي منطقة على شكل قرعة، تقع خارج أفق الحدث. لا يمكن أن تبقى الأجسام ثابتة ضمنها.[86]

يحيط بالثقوب السوداء الدوارة منطقة زمكان يستحيل الوقوف بثبات ضمنها ، تُسمى إرغوسفير أو منطقة العمل (أرغو كلمة إغريقية تعني العمل). وهي ناتجة عن آلية تعرف باسم جر الإطار أو تباطؤ الإطار، تتنبأ النسبية العامة بأن أي كتلة دوارة تميل إلى جر الزمكان المحيط بها بشكل مباشر. سوف يميل أي كائن بالقرب من الكتلة الدوارة إلى التحرك في نفس اتجاه الدوران. بالنسبة إلى الثقب الأسود الدوار، يكون هذا التأثير قويًا جدًا بالقرب من أفق الحدث ، بحيث يتحتم على الجسم أن يتحرك بسرعة أكبر من سرعة الضوء في الاتجاه المعاكس حتى يظل ثابتًا.[55]

إرغوسفير الثقب الأسود هو حجم يشكل سطحه الداخلي أفق الحدث الكروي والمفلطح للثقب الأسود وتكون الحدود الخارجية على شكل القرع، وتكون متزامنة مع أفق الحدث عند القطبين ولكنها أوسع بشكل ملحوظ حول خط الاستواء. في بعض الأحيان تسمى الحدود الخارجية سطح إرغو ergosurface .[86]

الأجسام والإشعاعات يمكن أن تفلت من الإرغوسفير. فمن خلال آلية بنروز، يمكن أن تخرج الأجسام من الإرغوسفير حاملة طاقة أكثر مما دخلت بها. هذه الطاقة مأخوذة من الطاقة الدورانية للثقب الأسود مما يتسبب في إبطاء دوران الثقب الأسود.[55] تعد عملية آلية بلاندفورد-زينديك ‏ هي الآلية المحتملة لحدوث اللمعان الهائل والنفاثات النسبية للكوازارات وغيرها من النوى المجرية النشطة، و ذلك كأحد تفسيرات آلية بنزور أثناء وجود حقول مغناطيسية قوية.

أقصى مدار دائري داخلي مستقر (ISCO)

ضمن الجاذبية النيوتونية، يمكن لجسيمات الاختبار أن تدور بثبات ضمن أي مدارات وبأي بعد عن جسم مركزي. لكن في النسبية العامة، يوجد مدار دائري مستقر (يُطلق عليه عادة ISCO)، بحيث يؤدي حدوث أي اضطرابات متناهية الصغر في المدار الدائري ضمنه إلى الدوران بسقوط داخل الثقب الأسود.[87] يعتمد موقع ISCO على دوران الثقب الأسود، في حالة وجود ثقب شوارزشيلد أسود (بدون دوران) يكون موقعه محددا بالمعادلة:

risco=3rs=6GMc2,

ويتناقص مع زيادة تدوير الثقب الأسود للجسيمات التي تدور في نفس اتجاه الدوران.[88]

التكوين والتطور

بالنظر إلى الطابع الغريب للثقوب السوداء، كان هناك تساؤل طويل حول ما إذا كانت هذه الأشياء يمكن أن توجد بالفعل في الطبيعة أو ما إذا كانت مجرد حلول خيالية لمعادلات آينشتاين. اعتقد آينشتاين نفسه خطأً أن الثقوب السوداء لن تتشكل، لأنه رأى أن الزخم الزاوي للجزيئات المنهارة من شأنه أن يثبّت حركتها عند بعض دائرة بنصف قطر معين.[89] وقد أدى ذلك إلى رفض مجتمع النسبية العام جميعَ النتائج التي تصر على عكس رأي آينشتاين لسنوات عديدة. ومع ذلك ، استمرت أقلية من الباحثين في الادعاء بأن الثقوب السوداء هي أجسام مادية حقيقية،[90] ومع نهاية الستينيات، أقنعوا غالبية الباحثين في هذا المجال بعدم وجود عقبة أمام تشكيل أفق الحدث.

أظهر بينروز أنه بمجرد تشكل أفق الحدث، تتطلب النسبية العامة بدون ميكانيكا الكم أن تتكون نقطة التفرد.[45] بعد ذلك بوقت قصير، أظهر هوكينج أن العديد من الحلول الكونية التي تصف الانفجار الكبير تحتوي تفردات بدون حقول سلمية أو غيرها من المواد الغريبة (انظر «نظريات تفرد بينروز - هوكينج»).[بحاجة لتوضيح] أظهر حل كير ونظرية انعدام الشعر ‏ وقوانين الديناميكا الحرارية للثقب الأسود أن الخصائص الفيزيائية للثقوب السوداء كانت بسيطة ومفهومة، مما جعلها مواضيع محترمة للبحث.[91] تتشكل الثقوب السوداء التقليدية عن طريق الانهيار التثاقلي للأجسام الثقيلة مثل النجوم، ولكن من الناحية النظرية، يمكن أيضًا تشكيلها بواسطة عمليات أخرى.[92][93]

الانهيار الجاذبي

يحدث انهيار الجاذبية عندما يكون الضغط الداخلي للكائن غير كافٍ لمقاومة جاذبية الجسم. يحدث هذا للنجوم عادة إما لأن النجم لديه القليل من «الوقود» المتبقي للحفاظ على درجة حرارته من خلال التخليق النووي النجمي، أو لأن النجم الذي كان مستقراً تلقى مادة إضافية بطريقة لم ترفع درجة حرارته الأساسية. في كلتا الحالتين لا تعتبر درجة حرارة النجم مرتفعة بما فيه الكفاية لمنعه من الانهيار تحت وطئ وزنه.[55] قد يتوقف الانهيار بضغط تنكس مكونات النجم، مما يسمح بتكثيف المادة إلى حالة غريبة أكثر كثافة. والنتيجة هي واحدة من الأنواع المختلفة من النجوم المتراصة. يعتمد الشكل النهائي على كتلة بقايا النجمة الأصلية التي بقيت بعد أن تم تفجير الطبقات الخارجية. مثل هذه الانفجارات والنبضات تؤدي إلى تكوين السديم الكوكبي .[94] هذه الكتلة يمكن أن تكون أقل بكثير من النجم الأصلي. البقايا التي تتجاوز 5 M☉ تنتج من النجوم التي كانت أضخم من 20 M☉ قبل حدوث الانهيار.[55]

إذا تجاوزت الكتلة المتبقية حوالي 3–4 M☉ ( حد تولمان - أوبنهايمر- فولكوف[26]) ، إما لأن النجم الأصلي كان ثقيلًا جدًا أو لأن البقايا جمعت كتلاً إضافية من خلال تراكم المواد من حولها، فوقتها لن يكون ضغط تنكس النيوترونات كافٍ لوقف الانهيار. لا توجد آلية معروفة (باستثناء ضغط تنكس الكواركات ، راجع نجم الكوارك) لها القوة بما يكفي لإيقاف الانهيار وسيؤدي إنهيار النجم لتشكيل حتمي لثقب أسود.[55]

رسم تخيلي لبذرة ثقب أسود هائل [95]

يفترض أن الانهيار الثقيل للنجوم الثقيلة هو المسؤول عن تشكيل الثقوب السوداء ذات الكتلة النجمية . قد يكون تكوين النجوم في بداية الكون قد أدى إلى نجوم ضخمة للغاية ، والتي عند انهيارها كانت ستنتج ثقوبًا سوداء تصل إلى 103 M☉. يمكن أن تكون هذه الثقوب السوداء هي ما شكل الثقوب السوداء الهائلة الموجودة في مراكز معظم المجرات.[96] وقد اُقترح كذلك أن الثقوب السوداء الهائلة ذات الكتل ~ 105 M☉ يمكن أن يكون قد تكونت بسبب الانهيار المباشر لسحب الغاز بداية تكون الكون.[92] تم العثور على بعض الثقوب المرشحة خلال عمليات رصد الكون الحديث.[92]

معظم الطاقة المنبعثة خلال انهيار الجاذبية تنبعث بسرعة كبيرة لكن المراقب الخارجي لا يرى فعليًا نهاية هذه العملية. فعلى الرغم من أن الانهيار يستغرق وقتًا محدودًا من الإطار المرجعي للمواد المنهارة، فإن المراقب البعيد سيرى أن المادة المنهارة بطيئة وتتوقف فوق أفق الحدث مباشرةً، بسبب الإبطاء الزمني الثقالي. يستغرق ضوء المادة المنهارة وقتًا أطول للوصول إلى المراقب، والضوء الذي انبعث لحظة تشكل أفق الحدث سيأخذ وقتا لا نهائيا ليصل. وبالتالي فإن المراقب الخارجي لن يرى أبداً لحظة تشكل أفق الحدث ؛ بدلاً من ذلك، سيبدو أن المواد المنهارة أصبحت أكثر خفوتًا وتحولت بشكل متزايد إلى اللون الأحمر، ثم تلاشت في النهاية.[97]

الثقوب السوداء البدائية والانفجار الكبير

يتطلب حدوث انهيار الجاذبية كثافة كبيرة. في العصر الحالي للكون توجد هذه الكثافة العالية فقط ضمن النجوم، ولكن في الكون المبكر بعد فترة وجيزة من الانفجار الكبير كانت الكثافات أكبر بكثير، مما سمحَ بإحداث ثقوب سوداء. الكثافة العالية وحدها لا تكفي للسماح بتكوين الثقب الأسود لأن توزيع الكتلة بشكل متوازن لم يكن ليسمح للكتلة بالتجمع. لكي تتشكل الثقوب السوداء البدائية في مثل هذه الوسيلة الكثيفة، كان يجب أن يكون هناك اضطرابات في الكثافة الأولية يمكن لها أن تنمو بعد ذلك تحت ثقلها. تختلف النماذج المختلفة للكون المبكر اختلافًا كبيرًا في تنبؤاتها بحجم التقلبات. تتنبأ نماذج مختلفة بتكوين ثقوب سوداء بدائية تتراوح في الحجم من كتلة بلانك إلى مئات الآلاف من الكتل الشمسية.[93]

على الرغم من كون الكون في وقت مبكر كثيفًا للغاية - كثيف جدًا أكثر مما هو مطلوب عادة لتشكيل ثقب أسود - إلا أنه لم يتحول إلى ثقب أسود خلال الانفجار الكبير. لا تطبق نماذج الانهيار التثاقلي للأجسام ذات الحجم الثابت نسبيًا، مثل النجوم، على التوسع السريع في الفضاء مثل الانفجار الكبير.[98]

اصطدامات عالية الطاقة

حدث محاكاة في كاشف CMS: تصادم يمكن فيه إنشاء ثقب أسود متناهي الصغر

انهيار الجاذبية ليس هو العملية الوحيدة التي يمكن أن تخلق ثقوبًا سوداء. فمن حيث المبدأ، يمكن تشكيل الثقوب السوداء بسبب تصادمات عالية الطاقة تحقق كثافة كافية. لكن ومنذ عام 2002، لم يتم الكشف عن مثل هذه الأحداث، سواء بشكل مباشر أو غير مباشر بسبب نقص في توازن الكتلة في تجارب مسرّع الجسيمات.[99] هذا يعني أنه يجب أن يكون هناك حد أدنى لكتلة الثقوب السوداء. من الناحية النظرية، من المتوقع أن تقع هذه الحدود حول كتلة بلانك ( m P = √ثابت بلانك c/G ≈ 1.2 ≈ 2.2 ) ، حيث من المحتمل أن تبطل التأثيرات الكمومية تنبؤات النسبية العامة.[100] هذا من شأنه أن يجعل من فكرة تصنيع ثقوب سوداء غير محتمل على الكرة الأرضية أو بالقرب منها. ومع ذلك، تشير بعض التطورات في دراسات الجاذبية الكمية إلى أن كتلة بلانك يمكن أن تكون أقل من ذلك بكثير: على سبيل المثال، تضع بعض سيناريوهات عالم الطبيعة الحدود الدنيا عند 1 TeV/c2.[101] هذا من شأنه أن يسمح بإمكانية إنشاء ثقوب سوداء دقيقة في تصادمات الطاقة العالية التي تحدث عندما تضرب الأشعة الكونية الغلاف الجوي للأرض، أو ربما ضمن مصادم الهادرون الكبير في سيرن. هذه النظريات هي تخمينية للغاية، ونشوء الثقوب السوداء في العديد من هذه العمليات مُستبعد جداً.[102] حتى لو تم تشكيل ثقوب سوداء صغيرة، فمن المتوقع أن تتبخر خلال حوالي −25 ثانية، بدون أن تشكل أي تهديد للأرض.[103]

النمو

بمجرد تشكيل ثقب أسود، يمكن أن يستمر في النمو عن طريق امتصاص مادة إضافية. أي ثقب أسود سوف يقوم بامتصاص الغبار والغبار بين النجوم من المناطق المحيطة به. هذه هي العملية الأساسية التي من خلالها يبدو أن الثقوب السوداء الهائلة قد نمت إلى احجامها الحالية.[96] تم اقتراح عملية مماثلة لتكوين ثقوب سوداء متوسطة الكتلة تم العثور عليها في بعض المجموعات الكروية.[104] يمكن أيضًا أن تندمج الثقوب السوداء مع اجسام أخرى مثل النجوم أو حتى الثقوب السوداء الأخرى. يُعتقد أن هذا الأمر كان مهمًا، لا سيما في مرحلة النمو المبكر للثقوب السوداء الفائقة الكتلة، والتي يمكن أن تتشكل من تجميع العديد من الأجسام الأصغر.[96] وقد اقترح أيضاً أن هذه العملية كانت سبباً لنشوء بعض الثقوب السوداء المتوسطة الكتلة.[105][106]

التبخر

في عام 1974، تنبئ هوكينج أن الثقوب السوداء ليست سوداء تمامًا وإنما ينبعث منها كميات صغيرة من الإشعاع الحراري عند درجة حرارة ℏ c3/(8 π G M [./https://en.wikipedia.org/wiki/Bolzmann_constant kB])،[48] أصبح هذا التأثير معروفًا بإشعاع هوكينج. من خلال تطبيق نظرية المجال الكمومي على خلفية ثقب أسود ثابت، راى هوكينج أن الثقب الأسود يجب أن يصدر جزيئات تعكس طيف جسم أسود مثالي. ومنذ نشر هوكينج لتنبؤاته، تحقق الكثيرون الآخرون من تلك النتائج وذلك من خلال أساليب مختلفة.[107] إذا كانت نظرية هوكينج لإشعاع الثقب الأسود صحيحة، فهذا يعني أن الثقوب السوداء ستتقلص وتتبخر بمرور الوقت لأنها تفقد الكتلة بسبب انبعاث الفوتونات والجزيئات الأخرى.[48] تتناسب درجة حرارة هذا الطيف الحراري (درجة حرارة هوكينج) مع الجاذبية السطحية للثقب الأسود، والتي تتناسب عكسياً مع الكتلة (في ثقب شوارزشيلد الأسود). وبالتالي، فإن الثقوب السوداء الكبيرة تنبعث منها إشعاعات أقل من تلك المنبعثة من الثقوب السوداء الصغيرة.[55]

ثقب أسود نجمي من 1 M☉ لديه درجة حرارة هوكينج 62   نانوكيلفين.[108] هذا أقل بكثير من قيمة 2.7 كيلفين لإشعاع الخلفية الميكروويفية للكون. تكتسب الثقوب ذات الكتلة النجمية أو الثقوب السوداء الأكبر حجمًا من خلفية الميكروويف الكونية أكثر مما تخسر من خلال إشعاع هوكينج، وبالتالي ستنمو بدلاً من أن تنكمش.[109] للحصول على درجة حرارة هوكينج أكبر من 2.7   K (وليكون قادرًا على التبخر)، سيحتاج الثقب الأسود إلى كتلة أقل من كتلة القمر وسيكون بقطر أقل من عُشر المليمتر.[110]

إذا كان الثقب الأسود صغيرًا جدًا، فمن المتوقع أن يصبح تأثير الإشعاع قويا جدًا. ثقب أسود بوزن يقارب وزن الإنسان سوف يتبخر في لحظة. يبلغ قطر الثقب الأسود بكتلة السيارة حوالي 10−24 م ويحتاج نانو ثانية ليتبخر، وخلال هذه الفترة سيملك لمعان أكثر من 200 مرة من لمعان الشمس. من المُعتقد أن تبخر الثقوب السوداء المنخفضة الكتلة يحدث بشكل أسرع. على سبيل المثال، ثقب أسود بكتلة 1 TeV/c سيستغرق أقل من 10−88 ثانية ليتبخر تمامًا. بالنسبة لمثل هذا الثقب الأسود الصغير، من المتوقع أن تلعب تأثيرات الجاذبية الكمية دورًا مهمًا ومن الممكن افتراضيًا أن تجعل من هذه الثغرة السوداء الصغيرة مستقرة، على الرغم من أن الدراسات الحالية في الجاذبية الكمية لا تشير إلى ذلك.[111][112]

من المتوقع أن يكون إشعاع هوكينج لثقب أسود فلكي ضعيفًا جدًا وبالتالي سيكون من الصعب للغاية اكتشافه من الأرض. الاستثناء المحتمل هو هبّات أشعة غاما المنبعثة في المرحلة الأخيرة من تبخر الثقوب السوداء البدائية. أثبتت عمليات البحث عن هذه الهبّات نجاحها وأعطت حدودا ً ارمة لإمكانية وجود ثقوب سوداء بدائية منخفضة الكتلة.[113] يواصل مرصد فيرمي الفضائي لأشعة غاما والذي أطلقته ناسا عام 2008 البحث عن هذه الهبات.[114]

إذا تبخرت الثقوب السوداء عبر إشعاع هوكينج ، فإن ثقباً أسوداً بكتلة الشمس سوف يتبخر (يبدأ بمجرد أن تنخفض درجة حرارة خلفية الميكروويف الكونية دون درجة حرارة الثقب الأسود) على مدى 1064 سنة.[115] ثقب أسود هائل بكتلة من 10 11 (100 مليار) M☉ سيتبخر في حوالي 2 × 10 100 سنة.[116] وتوقع لبعض الثقوب السوداء العملاقة في الكون أن تستمر في النمو حتى تصل إلى 10 14 M☉ إلى فترة انهيار العناقيد المجرية الهائلة. وحتى هذه سوف تتبخر على مدى زمني يصل إلى 10 106 سنة.[115]

الأدلة الرصدية

بحكم طبيعتها، لا ينبعث من الثقوب السوداء مباشرة أي إشعاع كهرمغنطيسي بخلاف إشعاع هوكينج الافتراضي، لذلك يتوجب على علماء الفيزياء الفلكية الذين يبحثون عن الثقوب السوداء الاعتماد عمومًا على الملاحظات غير المباشرة. على سبيل المثال، يمكن في بعض الأحيان الاستدلال على وجود ثقب أسود من خلال مراقبة تفاعلاتها الجاذبية مع محيطها.[117]

في 10 أبريل 2019، تم نشر أول صورة لثقب أسود تم رؤيته بصورة مكبرة لأن مسارات الضوء بالقرب من أفق الحدث شديدة الانحناء. ينتج الظل الداكن في الوسط عن مسارات الضوء التي يمتصها الثقب الأسود. محتوى الصورة من اللون كان مضافا، فهالة الضوء المكتشفة في هذه الصورة ليست في الطيف المرئي، ولكن ضمن موجات الراديو اللامرئية.

يصور انطباع هذا الفنان مسارات الفوتونات بالقرب من الثقب الأسود. إن ثني الجاذبية والتقاط الضوء من أفق الحدث هو سبب الظل الذي تم التقاطه بواسطة تلسكوب أفق الحدث

يعد تلسكوب أفق الحدث (EHT) الذي يديره مرصد هايستاك ‏ في معهد ماساتشوستس للتكنولوجيا، برنامجًا نشطًا يلاحظ بشكل مباشر البيئة المباشرة لأفق أحداث الثقوب السوداء، مثل الثقب الأسود في وسط درب التبانة. في أبريل 2017، بدأ التلسكوب بمراقبة الثقب الأسود في وسط ميسيه 87.[118] "في المجمل، راقبت ثمانية مراصد راديوية تقع على ستة جبال ضمن أربع قارات المجرة في برج العذراء بشكل متقطع لمدة 10 أيام في أبريل 2017" موفرة البيانات التي أدت لتوليد الصورة، بعد عامين، في أبريل 2019.[119] فبعد عامين من معالجة البيانات، أصدرت EHT أول صورة مباشرة لثقب أسود، وتحديداً الثقب الأسود الهائل الذي يقع في وسط مجرة مسييه 87.[120][121] ما هو مرئي ليس الثقب الأسود الذي يظهر باللون الأسود، بل الغازات على حافة أفق الحدث، والتي تظهر باللون البرتقالي أو الأحمر، وبالتالي تحدد مكان الثقب الأسود.[122] علقت عالمة الفيزياء الفلكية فريال أوزيل، عضو الفريق، على هذه الصورة ونظرية النسبية العامة: لمجرد أن هذه الصورة الأولى تدعم النسبية العامة "لا تعني أن النسبية العامة جيدة تمامًا“.[122]

قبل ذلك، في عام 2015، اكتشفت EHT حقولًا مغناطيسية خارج أفق حدث الرامي A*، بل وكانت قادرة على تمييز بعض خصائصها. تم التنبؤ بوجود مجالات مغناطيسية من خلال الدراسات النظرية للثقوب السوداء.[123][124]

منظر متوقع لثقب أسود لا يدور مع منطقة حلقية من المادة المتأينة، وهو ما تم اقتراحه [125] كنموذج لـ القوس القوس A * . يرجع عدم التماثل إلى تأثير دوبلر الناتج عن السرعة المدارية الهائلة اللازمة لتحقيق التوازن في الطرد المركزي لجاذبية الثقوب القوية للغاية.

الكشف عن موجات الجاذبية من دمج الثقوب السوداء

في 14 سبتمبر 2015، تمكن مرصد ليجو للموجات الجاذبية من رصد أول ملاحظة مباشرة تشير إلى موجات الجاذبية .[8][126] كانت الإشارة متسقة مع التنبؤات النظرية للموجات التثاقلية الناتجة عن اندماج ثقبين أسودين: ثقب بكتلة تقارب 36 كتلة شمسية والأخر بكتلة تقارب 29 كتلة شمسية.[8][127] وفر ذلك الرصد أفضل الأدلة الأكثر إثباتًا على وجود ثقوب سوداء حتى تاريخه. فعلى سبيل المثال، تشير إشارة موجة الجاذبية إلى أن المسافة الفاصلة بين الثقبين قبل الاندماج كان 350 كم (أو ما يقرب من 4 أضعاف نصف قطر شوارزشيلد المقابلة للكتل المُحتسبة). لذلك وجب أن تكون تلك الأجسام مضغوطة للغاية، مما يترك الثقوب السوداء كالتفسير المنطقي الوحيد لتلك الكتل.[8]

والأهم من ذلك هو أن الإشارة التي لاحظها مرصد ليجو تضمنت أيضًا بداية رنين ما بعد الدمج، وهي الإشارة التي يتم إنتاجها عندما يستقر الجسم المضغوط (الحديث المنشأ) ضمن حالة ثابتة. يمكن القول إن طريقة الرنين هي الطريقة الأكثر مباشرة لمراقبة الثقوب السوداء.[128] من إشارة ليغو، كان من الممكن استخراج التردد ووقت التخميد للوضع السائد في الرنين. ومن هذه تم استنتاج الزخم الشامل والزاوي للكائن النهائي، والذي يطابق التنبؤات المستقلة من المحاكاة العددية للاندماج.[129] يتم تحديد وقت تكرار وتسود الوضع المهيمن بواسطة هندسة كرة الفوتون. وبالتالي، فإن مراقبة هذا الوضع المهيمن أكد وجود كرة الفوتون. ومع ذلك لا يمكن أن تُستبعد البدائل الغريبة المحتملة للثقوب السوداء التي تكون مضغوطة بدرجة كافية للحصول على كرة فوتون.[128]

توفر الملاحظة أيضًا أول دليل مُلاحظي لوجود ثنائيات الثقب الأسود ذات الكتل النجمية. علاوة على ذلك، يُعد ذلك كأول دليل على وجود ثقوب سوداء ذات كتلة نجمية تصل إلى 25 كتلة شمسية أو أكثر.[130]

في 15 يونيو 2016، تم الإعلان عن اكتشاف ثان لحدث موجة الجاذبية من تصادم الثقوب السوداء،[131] ومنذ ذلك الحين تم التقاط موجات جاذبية أخرى ‏ .[10]

الحركة الصحيحة لنجوم تدور حول القوس A *

توفر الحركات المناسبة للنجوم القريبة من مركز درب التبانة دليلًا قويًا على أن هذه النجوم تدور حول ثقب أسود هائل.[132] منذ عام 1995، قام علماء الفلك بتتبع حركات 90 نجمًا تدور حول جسم غير مرئي يتزامن مع مصدر الراديو الرامي A* . من خلال تطبيق حركاتها على معادلات الامدارات الكبلرية، استنتج علماء الفلك، في عام 1998، وجود جسم بكتلة تصل إلى 2.6 مليون M ☉ وبجم يصل نصف قطره إلى 0.02 سنة ضوئية، وذلك لتفسير حركة تلك النجوم.[133] ومنذ ذلك الوقت، أكمل أحد النجوم - يسمى S2 - مدارا كامل حول الجسم المتوقع. من البيانات المدارية، كان العلماء قادرين على تصحيح حساب الكتلة إلى 4.3 مليون M☉ وتصحيح قيمة نصف قطرها إلى أقل من 0.002 سنة ضوئية ليصبح ذلك الجسم المخفي قادرا على فرض تلك الحركة المدارية على النجوم التي تتبع حركة.[132] لا يزال الحد الأعلى لحجم الكائن أكبر من لإمكانية اختبار ما إذا كان أصغر من نصف قطر شفارتزشيلد الخاص به؛ ومع ذلك ، فإن هذه الملاحظات تشير بقوة إلى أن الجسم المركزي هو ثقب أسود هائل، حيث لا توجد سيناريوهات أخرى معقولة لحصر الكثير من الكتلة غير المرئية ضمن هذا الحجم الصغير.[133] بالإضافة إلى ذلك، هناك بعض الأدلة التي تم ملاحظتها و التي تشير إلى أن هذا الجسم قد يمتلك أفق الحدث، الميزة الفريدة للثقوب السوداء.[134]

تراكم المادة

ثقب أسود مع الهالة، ومصدر لأشعة سينية (تخيل للرسام).[135]

بسبب مبدأ الحفاظ على الزخم الزاوي، [136] لإإن الغاز الذي يسقط في البئر التثاقلي الناتج عن جسم ضخم سوف يشكل بنية تشبه القرص حول ذلك الجسم. إن تخيلات الفنانين لشكل ذلك القرص حول الثقب الأسود، عادةً ما يتم ترجمتها كما لو كان جسمًا مسطحًا يخفي جزءًا من القرص خلفه مباشرةً ، ولكن الواقع مختلف، فالعدسات الجاذبية ستشوه إلى حد كبير صورة قرص التراكم.[137]

منظر متوقع من خارج أفق ثقب أسود في شفارتزشيلد مضاء بواسطة قرص تراكم رفيع

قد يتسبب الاحتكاك، داخل هذا القرص، بنقل الزخم الزاوي للخارج، مما يسمح بتراجع المادة إلى الداخل ، وبالتالي إطلاق طاقة الوضع وزيادة درجة حرارة الغاز.[138]

عدم وضوح الأشعة السينية بالقرب من الثقب الأسود ( نوستار ، 12 أغسطس 2014).[135]

عندما يكون الجسم التراكم نجمًا نيوترونيًا أو ثقبًا أسود، فإن الغاز الموجود في قرص التراكم الداخلي يدور بسرعات عالية جدًا نظرًا لقربه من الجسم المضغوط. الاحتكاك الناتج مؤثر للغاية لدرجة أنه يرفع حرارة القرص الداخلي إلى درجات حرارة تنبعث منها كميات هائلة من الإشعاع الكهرومغناطيسي (الأشعة السينية بشكل رئيسي). يمكن الكشف عن مصادر الأشعة السينية الساطعة هذه بواسطة التلسكوبات. عملية التراكم هذه هي واحدة من أكثر العمليات المعروفة كفاءة في إنتاج الطاقة؛ حيث يمكن أن ينبعث ما يصل إلى 40٪ من كتلة المواد المتراكمة كإشعاع.[138] (في الانصهار النووي، يتم تحويل حوالي 0.7٪ فقط من الكتلة إلى طاقة ). في الكثير من الحالات، تترافق أقراص التراكم مع نفاثات نسبية تنبعث على طول الأقطاب، حاملة الكثير من الطاقة. آلية إنشاء هذه النفاثات غير مفهومة بشكل جيد في الوقت الحالي ، ويعزى ذلك جزئيًا إلى عدم كفاية البيانات.[139]

وعليه، فإن العديد من ظواهر الكون الأكثر حيوية تنسب إلى آلية تراكم المادة على الثقوب السوداء. على وجه الخصوص، يُعتقد أن النوى المجرية والكوازارات النشطة هي أقراص تراكم الثقوب السوداء الفائقة الكتلة.[140] وبالمثل ، من المقبول عمومًا أن تكون ثنائيات الأشعة السينية أنظمة نجوم ثنائية يكون فيها أحد النجومين عبارة عن جسم مضغوط يتراكم من رفيقه.[140] وقد اُقترح أن بعض مصادر الأشعة السينية فائقة السطوع قد تكون ناتجة عن أقراص تراكم الثقوب السوداء المتوسطة الكتلة .[141]

في نوفمبر 2011، تم تسجيل أول ملاحظة مباشرة لقرص تراكم النجوم حول ثقب أسود هائل.[142][143]

تاريخ مفهوم الثقوب السوداء

صورة خيالية لثقب أسود.

كان طرح فرضية إمكانية وجود مثل هذه الظاهرة هو اكتشاف رومر أن للضوء سرعة محددة، وطرح هذا الاكتشاف تساؤلاً وهو لماذا لا تزيد سرعة الضوء إلى سرعة أكبر؟ وفُسِّر ذلك على أنه قد يكون للجاذبية تأثير على الضوء، وكتب جون مينشل من هذا الاكتشاف مقالاً عام 1783 م أشار فيه إلى أنه قد يكون للنجم الكثيف المتراص جاذبية شديدة جدًا حتى أن الضوء لا يمكنهُ الإفلات منها فأي ضوء ينبعث من سطح النجم تعيده هذه الجاذبية.[144]

وهناك فرضية تقول أيضًا أنه يوجد نجوم عديدة من هذه النجوم لا يمكننا أن نرى ضوءها؛ لأنها لا تبعثه لكننا نستطيع أن نتحسس جاذبيتها، وهذه النجوم هي ما نسميها بـ الثقوب السوداء أي الفجوات في الفضاء، وقد أهملت هذه الأفكار؛ لأن النظرية الموجية للضوء كانت سائدة في ذلك الوقت، وأعاد العالم الفرنسي بيير سيمون لابلاس هذه الفكرة إلى الواجهة في 1796 م في كتابه Exposition du Système du Monde (مقدمة عن النظام الكوني)[145][146] ولكن معاصريه شككوا في صحة الفكرة لهشاشتها النظرية[147] إلى أن جاءت نظرية النسبية العامة لألبرت أينشتاين التي برهنت على إمكانية وجود الثقوب السوداء.[148]

وبعد ذلك بدأ علماء الفلك في البحث عن آثارها باستخدام التلسكوبات الأرضية والفضائية حيث تم اكتشاف أن نجم الدجاجة إكس-1 يرجح أن يكون ثقب أسود محتمل سنة 1971 م،[149] وتحولت الآراء حول الثقب الأسود إلى حقائق مشاهدة عبر المقراب الفلكي الراديوي الذي يتيح للراصدين مشاهدة الكون بشكل أوضح، وجعل نظرية النسبية حقيقة علمية مقبولة عند معظم دارسي علوم الفيزياء.[150][151]

ثقوب سوداء عظيمة الكتلة

الرامي أ* وIRS 13 في مركز المجرة.
سحابة غازية في طريقها إلى ثقب أسود في مركز المجرة (Video).

تبلغ كتلة ثقوب سوداء عظيمة الكتلة بين ملايين كتلة شمسية إلى مليارات كتلة شمسية، ويبدو أنها تتواجد في معظم الحالات في مراكز المجرات، وكيفية تكون تلك الثقوب السوداء وعلاقتها بتكوّن مجرة حولها لا يزال تحت بحث علماء الفلك.

يوجد مصدر راديوي شديد في مركز مجرتنا مجرة درب التبانة يشع أشعة راديوية غزيرة وهو يسمى الرامي أ* (أو مختصرا Sgr A* أو بالعربية: «الرامي أ*») وتبلغ كتلته نحو 4.3 مليون كتلة شمسية،[152] وكان تقدير كتلته قبل سنوات معتمدًا على مشاهدات سحب غازات بالقرب منه (مثل ما يسمى ذراع حلزوني صغير) أدت إلى أن تبلغ كتلته 2.7 مليون كتلة شمسية ولكن استخدام تلسكوبات ذات تباين أعلى وحساسية أشد استطاع العلماء استنتاج كتلته في مركز المجرة عن طريق مشاهدة مدارات نجوم قريبة منه وسرعاتها في مداراته حوله مثل S0-102 ونجم إس 2، وقد بينت المشاهدات الحديثة إلى أن كتلته أكبر بكثير؛ فهي تبلغ 4.3 مليون كتلة شمسية.

تشير المشاهدات إلى أن الثقوب السوداء قد تكونت مع تكون المجرات في وقت واحد وأنها قد ساعدت على تكون مجرة حولها، وهذا موضوع هام يهتم به العلماء لتفسيره.

إن مصدر راديوي الرامي A* ( للاختصار Sgr *A ) في وسط مجرة درب التبانة هو ثقب أسود هائل كتلته 4.3 مليون كتلة شمسية.[153] قبل بضع سنوات ، يعتمد تقدير الكتلة على مراقبة سحب الغاز (على سبيل المثال ، يسمى mini-spiral) ، لا يزال عند حوالي 2.7 مليون من الكتل الشمسية. بفضل الدقة المحسّنة وحساسية التلسكوبات ، يمكن تحديد كتلة الثقب الأسود في مركز المجرة بشكل أكثر دقة من خلال تحليل مسارات ، على سبيل المثال النجوم S0-102 أو S2 التي تدور حول الثقب الأسود .

طور الباحثان ناتارجان و تريستر [154] نموذجًا للكتلة العليا حد في الترتيب من حيث الحجم 10 مليار كتلة شمسية. والسبب هو - بناء على شرح وصفي - أن المادة المتساقطة تتسارع من خلال قوة الجاذبية لمثل هذا الثقب الأسود الهائل بطريقة تؤدي إلى ظهور قطر مستقر خارج نصف قطر شفارتزشيلد. بالإضافة إلى ذلك ، يعمل الإشعاع الكهرومغناطيسي و «رياح المادة» المنبعثة من المادة في قرص التراكم كمقاومة لمزيد من المادة المتساقطة ، وفي النهاية ينشأ توازنًا بين المادة المتراكنة والمطرودة (انظر حد إدنجتون ).

الغموض الذي لم يتم حله هو تكوين الثقوب السوداء الهائلة في بدايات الكون. من المعروف أنه بعد 700 مليون سنة من حدوث الانفجار العظيم ، وجدت ثقوب عملاقة تبلغ حوالي 2 مليار كتلة شمسية ، مثل (ULAS J1120+0641).[155] وهو أيضًا أبعد جسم معروف اعتبارًا من ديسمبر 2017 (ULAS J1342+0928 ) ، بعد أقل من 690 مليون سنة من الانفجار العظيم ، هو بالفعل ثقب أسود هائل.[156] يتفق معظم العلماء على أنها مكونة من ثقوب سوداء أصغر حجمًا تم إنشاؤها ، حيث يرى بعض العلماء هذه «كبذور» للثقوب السوداء، بحد أقصى بضع مئات من الكتل الشمسية ، والآخر في تلك التي تتكون من آلاف إلى عشرات الآلاف من الكتل الشمسية.إغلاق </ref> مفقود لوسم <ref> في سيناريوهات أخرى ، يمنع الضوء فوق البنفسجي المكثف من النجوم الشابة من المجرات المجاورة تكون النجوم في سحابة من الغاز حتى تنهار مباشرة في ثقب أسود من حوالي 100.000 كتلة شمسية.[157] من المتوقع أن يوفر مقراب جيمس ويب الفضائي مزيدًا من المعلومات حول النجوم وسحب الغاز في بدايات الكون.

في عام 2008 ، اكتشفت مجموعة علماء سويسريين من مدرسة لوزان الاتحادية للعلوم التطبيقية (EPFL) بقيادة ألكسندر إيجنبرود بنية حلقة عالية الطاقة حول كوازار على بعد 10 مليار سنة ضوئية ، صليب أينشتاين في الكوكبة بيغاسوس ، تم رصده من VLT وبالتالي يؤكد جيدًا نظرية الثقوب فائقة الكتلة.[158]

أكبر ثقب أسود معروف (اعتبارًا من يناير 2021) هو TON 618 عبارة عن (نجم زائف) ذو كتلة تقدر بنحو 66 إلى 70 مليار كتلة شمسية ، يليه الثقب الأسود المركزي للمجرة IC 1101 بحوالي 40 مليار كتلة شمسية.[159] يوجد مثال آخر لحوالي 21 مليار كتلة شمسية في مركز المجرة NGC 4889 (2011) . مع وجود ثقب أسود فائق الكتلة يبلغ حوالي 20 مليار كتلة شمسية إغلاق </ref> مفقود لوسم <ref> أيضًا أحد أكثر المرشحين شهرة حتى الآن.

تم اكتشاف ثقب أسود كتلته 6.6 مليار كتلة شمسية في مركز المجرة القريبة نسبيًا M87 (حوالي 55 مليون سنة ضوئية).[160][161]

تم العثور أيضًا على ثقوب سوداء فائقة الكتلة في المجرة القزمة فائقة الصغر (لأول مرة في عام 2014 في M60؛ - UCD 1) ، [162][163] مما يشير إلى أن هذه تشكلت على أنها مجرات "طبيعية" ، حيث انفصل جزء كبير من النجوم منها عن طريق الاصطدام بمجرات أكبر.

في سبتمبر 2017 ، تم نشر اكتشاف ثقب أسود فائق الكتلة ، والذي يمكن مشاهدته باستخدام قياس التداخل الأساسي الطويل جدًا (VLBI). هذان ثقبان أسودان يدوران حول بعضهما البعض تفصل بينهما مسافة 1.1 سنة ضوئية ، لهما كتلة إجمالية تبلغ 36 مليون كتلة شمسية في المجرة الحلزونية 7674 NGC.[164]

في عام 2015 ، وبالتعاون مع نوستار وXMM نيوتن ، تم اكتشاف أن الثقوب السوداء الهائلة تنبعث منها «رياح بلازما» (غازات من ذرات عالية الطاقة ومتأينة للغاية) في شكل متناظر كرويًا وأن هذه كافية بقوة لمنع تشكل نجوم على مساحات كبيرة من المجرة المضيفة. [38]

بسبب التناظر الكري ، فإنها تختلف اختلافًا كبيرًا عن الطائرات . وفي عام 2017 ، تم إثبات ذلك بواسطة مرصد كيك فقد تيبن أن رياح الثقوب السوداء (في هذه الحالة في كوازار Quasar 3C 298 على بٌعد 9.3 مليار سنة لديها القدرة على تشكيل مجرة المضيف بأكملها.[165][166][167] تحتوي المجرة على مائة فقط من الكتلة التي يمكن توقعها من العلاقة الطبيعية بين كتلة الثقوب السوداء الفائقة ومجراتها المضيفة.

تطور نجم

المقالات الرئيسية: ولادة النجوم ومستعر أعظم

يتكون النجم من سحابة من غاز الهيدروجين (والقليل من الهيليوم) تبدأ بالتجمع والتكدس على بعضها ثم بالدوران حول نفسها. ومع هذا التكثف يَزداد الضغط على نواتها بشكل كبير، فيَسخن الغاز في النواة حتى يصبح حاراً جداً إلى درجة أن تندمج ذرات الهيدروجين لتكونّ عنصر الهيليوم،[168] وبهذه العملية يَستطيع النجم توليد ضغط باتجاه الخارج في نواته يَمنعها من الانهيار على نفسها.[169] لكن عندما يَنفذ وقود النجم من الهيدروجين يُصبح مهدداً بالانهيار على نفسه نتيجة لضغط كتلته، فترتفع درجة حرارة قلب النجم إلى درجة يَبدأ فيها النجم تفاعلات اندماج تنتج الليثيوم ثم الكربون والنتروجين والأكسجين وصولاً إلى الحديد. فحينها لا يَعود النجم قادراً على دمجه إلى عناصر أثقل لأن الطاقة التي يُولدها الاندماج النووي لا تعود كافية لمنعه من الانهيار، فيَنهار على نفسه في انفجار المستعر الأعظم مطلقاً طاقة هائلة.[170]

لكن ما يُحدد مصير النجم بعد انفجاره هو ما يُسمى «حد تشاندراسيخار»، هذا الحد هو مقدار الكتلة (1.4 كتلة شمسية) الذي إن لم يَتجاوزه النجم فسيَتحول إلى قزم أبيض، وإن تجاوزه فيَتحول إما إلى نجم نيوتروني أو إلى ثقب أسود (ما يُحدد أيهما هو حد تولمان-أوبنهايمر-فولكوف).[171] إذا ما كانت كتلة النجم عالية، فسيَعني هذا أنه سيَكون أكثر كثافة، ولذلك فإن النجوم الكثيفة تصبح نجوماً نيوترونية أو ثقوباً سوداء. النجوم النيوترونية هي أجسام عالية الكثافة جداً، ولذا فعندما تتكون تندمج الإلكترونات والبروتونات لتصبح نيوترونات تستطيع تحمل الضغط الهائل في النواة (فقطر هذه النجوم لا يَتجاوز الـ20 كم)، أما عندما تكون الكثافة أعلى من ذلك، فإن حتى النيوترونات لا تعود قادرة على تحمل الضغط الهائل، فيَنهار النجم متحولاً إلى ثقب أسود هائل الكثافة.[172][173] تكثر النجوم في أذرعة مجرة حيث تشتد فيها كثافة سحب الغازات التي تتكون منها النجوم. وتدور النجوم في مدارات حول مركز مجرة، مثلما تدور الكواكب حول الشمس. وتبلغ دورة واحدة لمجرتنا حول مركزها نحو 250 مليون سنة.

الثقوب السوداء والنظرية النسبية

التشوهات الناتجة عن الجاذبية الهائلة للثقب الأسود أمام سحابة ماجلان الكبرى (تفسير تصوري)

أفق الحدث هو (حدود منطقة من الزمان والمكان التي لا يمكن للضوء الإفلات منها) وبما أنه لا شيء يمكنه السير بأسرع من الضوء، فإن أي شي يقع في هذه المنطقة سوف يبلغ بسرعة منطقة ذات كثافة عالية ونهاية الزمان.

وتتنبأ النسبية العامة بأن الأجسام الثقيلة المتحركة سوف تتسبب ببث موجات جاذبية وهي تموجات نتيجة إنحناء الفضاء (هذه التموجات هي ليست مثل موجات الراديو بل هي إنحناء وتقوس في بنية الزمكان تخيل أنك تمشي في بركة ماء سوف تتكون موجات من الماء بسبب حركة في البركة وهذه الموجات الناشئة هي مكانية ذات ثلاث أبعاد وموجة مثلها معها زمانية لتكون موجات من بعد رابع هي التي يقصد بها إنحناءات الفضاء) تنتقل بسرعة الضوء وتشبه موجات الضوء التي هي تموجات المجال الكهرمغناطيسي إلا أنها يصعب اكتشافها وهي كالضوء تأخذ الطاقة من الأجسام التي تبثها وبالتالي يتوقع أن ينهار نظام من الأجسام الضخمة ويعود في النهاية إلى وضع مستقر لأن الطاقة في أي حركة سوف تحمل بعيداً.

على سبيل المثال دوران الأرض حول الشمس يولد موجات جاذبية ويكون تأثير مسارات الطاقة في تغير مدار الأرض حول الشمس الذي يؤدي في آخر المطاف إلى أن الأرض تقترب من الشمس حتى تستقر داخلها ومعدل ضياع الطاقة ضئيل جداً.

وشوهد هذا التأثير في نظام النجم النابض وهو نوع خاص من النجوم النيوترونية تبث نبضات منتظمة من موجات الراديو، ويضم هذا النظام نجمين نيترونيين يدوران حول بعضهما البعض فيما يعرف بالنجوم المزدوجة.

شكل النجوم التي تكون منها الثقب الأسود

أحدث «ورنر إزرائيل» Werner Israel - وهو باحث كندي ولد في برلين – ثورة في دراسة الثقوب السوداء عام 1967 م عندما بيَّن أن الثقوب السوداء ليست دوارة، فوفقا للنظرية النسبية العامة إن كانت دوارة فلابد أن تكون كروية تماماً. ولا يتوقف حجمها إلا على كتلتها، وأي ثقبين سوداوين، بكتلة متساوية هما متساويان بالحجم. وقد أمكن وضعهما عن طريق حل خاص لمعادلات أينشتاين قبل النسبية العامة بقليل. وكان من المعتقد أن الثقب الأسود لا يتكون إلا عند انسحاق جسم كروي تماما. وأن النجوم ليست كروية تماما، ولا يمكن بالتالي أن يسحق إلا بشكل تفرد ثقاليا عاريا، لكن هناك تفسيرات مختلفة لنتيجة «إزرائيل» تبناها روجر بنروز و«جون ويلر» فقد أبديا أن الحركات السريعة في انسحاق النجم يعني أن موجات الجاذبية المنبعثة منه تجعله أكثر كروية إلى أن يستقر في وضع ثابت ويصبح كروياً بشكل دقيق. ووفق هذه النظرية فأن أي نجم دوار يصبح كرويا مهما كان شكله وبنيته الداخلية معقدتين، وسوف ينتهي بعد انسحاقه بالجاذبية إلى ثقب أسود كروي تماما يتوقف حجمه على كتلته فقط.[174][175] واكتشف أول نباض عام 1967 مؤيدا للنظرية النسبية.[176][177] وتبين ان تلك النباضات ما هي إلا نجوم نيوترونية. حتى ذلك الحين كانت النجوم النيوترونية والثقوب السوداء ترى على أنها أجسام نظرية ولا وجود لها في الطبيعة.

وخلال تلك الفترة كثرت حسابات النظرية النسبية التي تؤدي إلى امكانية نشأة ثقب أسود.[178] من خلال عمل ورنر إزرائيل وبراندون كارتر[179] ,[180][181][182] نشأت «نظرية لا شعر» والتي تشير إلى أن حل الثقب الأسود الثابت يمكن وصفه بثلاثة إحداثيات طبقا لمقياسية كتلة، والعزم الزاوي والشحنة الكهربائية.[80]

وكانت ظواهر الثقب الأسود المحسوبة بواسطة النظرية النسبية لا تزال تعتبر نظرية بحتة وناشئة عن شروط تناظر مفترضة في حل المعادلات. كان من العلماء الذين اعتنقوا تلك الفكرة فلاديمير بلينسكي وأيزاك خالاتنيكوف وافيجني ليفشيتز الذي حاول إثبات ظهور تلك الحلول في الحال العام أيضا. ولكن في الستينيات من القرن الماضي قام روجر بنروز[183] وستيفن هوكينغ باستخدام طريقة شاملة لإثبات أن حالة التفرد الثقالي تظهر أيضا في الحلول العامة لمعادلات النظرية النسبية العامة.[184]

وفي عام 1963 م، وجد «دوي كير» مجموعة من الحلول لمعادلات النسبية العامة تصف الثقوب السوداء الدوارة التي أغفلها «إزرائيل «. فإذا كانت الدورات صفر يكون الثقب الأسود كروي تماما ويصبح الحل مماثلاً لحل «شفارزشيلد». أما إذا كان الدوران ليس صفرا ينتفخ الثقب الأسود نحو الخارج قرب مستوى خط استوائه تماما مثل الأرض منبعجة من تأثير دورانها. لقد افترض إزرائيل أن أي جسم ينسحق ليكون ثقبا أسود سوف ينتهي إلى وضع مستقر كما يصف حل كير.

حجم الثقوب السوداء وأدلة وجودها

في عام 1970م بين «براندون كارتر» أن حجم وشكل أي ثقب أسود ثابت الدوران يتوقف فقط على كتلة ومعدل دورانه بشرط أن يكون له محور تناظر، وبعد فترة أثبت ستيفن هوكينغ أن أي ثقب أسود ذي دوران ثابت سوف يكون له محور تناظر. واستخدم «رو بنسون» هذه النتائج ليثبت أنه بعد انسحاق الجاذبية بان الثقب الأسود من الاستقرار على وضع يكون دواراً ولكن ليس نابضاً، وأيضا حجمه وشكله يتوقفان على كتلته ومعدل دورانه دون الجسم الذي انسحق ليكونه.

ولكن في وقتنا هذا تم رصد أحجام للثقوب السوداء بعد إكتشاف أكبر خمسة ثقوب سوداء في الفضاء الخارجي.

وهم كالترتيب التالي:

(1) NGC 1277

يُعد من أصغر الثقوب المستكشفة لوقتنا هذا حيت تبلغ الكتلة الشمسية لهذا الثقب إلى 5000,000,000 كتلة شمسية، بالإضافة إلى أنه يقع في كتلة 50% من كتلة المجرة التي يوجد بها ولكن يوجد ثقوب سوداء أكبر من ذلك.

(2) Holmberg 158

حيث تصل الكتلة الشمسية فيه إلى 10,000,000,000 كتلة شمسية وهو ثاني أكبر ثقب أسود مكتشف.

(3) OJ 278

تصل الكتلة الشمسية لهذا الثقب إلى 18,000,000,000 كتلة شمسية وهو ثالث أكبر ثقب أسود مكتشف.

(4) H1821+643

تصل الكتلة الشمسية لهذا الثقب إلى 30,000,000,000 كتلة شمسية وهو أكبر رابع ثقب أسود مكتشف.

(5) S50014+81

حيث تصل الكتلة الشمسية لهذا الثقب إلى 40,000,000,000 كتلة شمسية وهو أكبر ثقب أسود مكتشف.

ما الأدلة على وجود هذه الثقوب؟

لم يتوفر دليل على وجود الثقوب السوداء سوى حسابات مبنية على النسبية لذلك كان هناك من لم يُصدق بها. وفي عام 1963م، رصد «مارتن سميدت» وهو عالم فلكي أمريكي الانزياح نحو الأحمر في طيف جسم باهت يشبه النجم في اتجاه مصدر موجات الراديو فوجد أنه أكبر من كونه ناتج عن حقل جاذبية؛ فلو كان انزياحه بالجاذبية نحو الأحمر لكان الجسم كبير الكتلة وقريباً منا بحيث تنزاح مدرات الكواكب في النظام الشمسي. وهذا الانزياح نحو الأحمر ناتج عن توسع الكون وهذا يعني بدوره أن الجسم بعيدٌ جداً عنا ولكي يُرى على هذه المسافة الكبيرة لابد وأنه يَبث مقدار هائلاً من الطاقة، والتفسير الوحيد لهذا ناتج انسحاق بالجاذبية ليس لنجم واحد بل لمنطقة مركزية من إحدى المجرات بكاملها وتسمى أشباه النجوم.

في العاشر من أبريل لعام 2019 تم نشر أول صورة حقيقية لثقب أسود داخل نواة المجرة الأهليليجية العملاقة 87, حيث تم الإعلان عنها في مؤتمر بواسطة شبكة مقراب أفق الحدث.

الكوازارات

المقالة الرئيسية: نجم زائف

في عام 1967م اكتشفت «جوسلين بل» أجسام في الفضاء تبث نبضات منتظمة من موجات الراديو وكانت تعتقد أنها اتصلت مع حضارات غريبة في المجرة ولكنها توصلت إلى أن هذه النبضات ناتجة عن نجم نباض هو في الواقع نجوم نيترونية دوارة تبث هذه النبضات هي بسبب تداخل معقد بين حقولها الجاذبة وبين المادة المحيطة بها وهذه النبضات هي الدليل الأول على وجود الثقوب السوداء ولكن كيف يمكن لنا اكتشاف أو استشعار الثقب الأسود مع أنه لا يبعث الضوء؟ ذلك عن طريق دراسة القوة التي يمارسها الثقب الأسود على الأجسام المجاورة فقد شاهدوا نجماً يدور حول آخر غير مرئي ولكن ليس هذا شرطًا أن يكون النجم غير المرئي ثقباً أسوداً فقد يكون نجماً باهتاً.

ومع هذه الجاذبية العالية والطاقة الهائلة التي يبثها الثقب الأسود فإنه قد تتولد جسيمات ذات طاقة عالية جداً قرب الثقب الأسود ويكون الحقل المغناطيسي شديداً بحيث تتجمع الجسيمات في نفاثتين متضادتين تنطلقان خارجاً على طول محور الدوران، ونشاهد مثل هذه الجسيمات في عدد من الكوازارات.

إشعاع الثقب الأسود

من فكرة تعريف الثقب الأسود كمجموعة من الأحداث التي لا يمكن الإفلات منها بعيداً، ويعني أن الثقب الأسود أي أفق الحدث مكون من مسارات أشعة الضوء في الزمكان وبالتالي لا يستطيع الضوء الابتعاد عن الثقب الأسود بل يحوم عند أطرافه إلى الأبد. إن هذه المسارات لا يمكن أن تقترب من بعضها البعض فإذا اقتربت فلابد أن تندمج لتصبح واحدة، وفي هذه الحالة تقع في ثقب أسود، ولكن إذا ابتلع الثقبُ الأسود هذه الأشعة فهذا يعني أنها لم تكن على حدوده، وهذا يعني أنه يجب أن تكون الأشعة متوازية أو متباعدة، وإذا كانت الأشعة التي يتألف منها أفق الحدث لا يمكنها أن تتقارب فإن مساحة أفق الحدث تبقى كما هي أو تتسع مع الزمان، وفي الواقع تتسع المساحة كلما وقع في الثقب الأسود مادة أو إشعاع وإذا تصادم ثقبان أسودان واندمجا معا في ثقب واحد فإن مساحة أفق حدث للثقب الجديد تساوي مجموع مساحتي الثقبين الأوليين أو أكبر، وبناءً على هذا التعريف وهذه الفكرة فسوف تكون حدود الثقب الأسود هي للثقب الأسود وأيضا مساحتهما بشرط أن يكون الثقب الأسود قد صار إلى وضع مستقر لا يتغير مع الزمن، كان هذا السلوك لمساحة الثقب الأسود مستوحى إلى حد بعيد من سلوك مقدار مادي يدعى «أنتروبيا» - وهو مقياس درجة خلل أو اضطراب نظام ما - ويعرف تقدير أو وصف هذه الفكرة الدقيقة بالقانون الثاني للديناميكا الحرارية فهو ينص على أن «الأنتروبيا» لنظام معزول تتزايد باطراد وعندما يندمج نظامان معا، تكون «أنتروبيا» النظام الموحد، أكبر من مجموع الأثنين في كل منهما، واقترح طالبُ أبحاث اسمه «جاكوب بكنشتاين» أن مساحة أفق الحدث هي مقياس أنتروبيا للثقب الأسود؛ فكلما سقطت فيه مادة تحمل أنتروبيا كلما أتسعت مساحة أفق الحدث ’بحيث أن مجموع أنتروبيا المادة خارج الثقوب السوداء ومساحة الآفاق لا تنقص أبدا، فإذا كان للثقب الأسود أنتروبيا فلابد أن تكون له حرارة، كذلك كل جسم ذي حرارة معينة لابد أن يبث إشعاع بمعدل ما وهذا الإشعاع ضروري لتفادي خرق القانون الثاني للديناميكا. أي أنه يجب أن تبث الثقوب السوداء إشعاعاً ولكن الثقوب السوداء بحكم تعريفها بالذات أجسام يفترض أن لا تبث شيئاً.

وفي الحقيقة الثقوب السوداء الدوارة تبث جسيمات ذرية، ولكن عندما أجرى ستيفن هوكينغ حساباته ظهرت له نتيجة مزعجة وهي أنه حتى الثقوب السوداء غير الدوارة تبث جسيمات ذرية وهذه النتيجة كان يعتقد ستيفن أنها ناتجة عن اعتماده تقديراً خاطئاً وأخيراً أكد له طيف هذه الجسيمات هو بالضبط ما قد يصدر عن جسم حار.

كيف يبدو أن الثقب الأسود يمكنه بث جسيمات ما دمنا نعرف أن لا شي يمكنه الإفلات من أفق الحدث؟ الجواب كما تفيد نظرية الكم هو إن الجسيمات لا تصدر من داخل الثقب الأسود بل من (الفراغ) الفضاء الفارغ خارج أفق الحدث للثقب الأسود مباشرة، وكي تتضح الصورة لابد من إعادة فكرة إن ما نخاله فضاءاً فارغاً، لا يمكن أن يكون فراغاً تماماً لأن ذلك يعني إن جميع الحقول من الجاذبية والكهرومغناطيسية ستكون صفراً بالضبط إلا أن قيمة الحقل ومعدل تغيره مع الزمن يشبهان موقع وسرعة الجسم: فمبدأ عدم التأكد يحتم أنه كلما قمنا بقياس واحدة من هاتين الكميتين بدقة عالية كلما تناقصت دقة قياس الكمية الأخرى. ففي فضاء فارغ لا يمكن تحديد الحقل صفراً بدقة لأنه تكون له قيمة صفر ومعدل تغير صفر، وهذا مخالف لمبدأ عدم التأكد. إذاً لابد أن تكون هناك جسيمات أولية في الفضاء تظهر تارة وتختفي تارة، وهي حينما تفعل ذلك فهي تظهر على هيئة زوجٍ من الجسيمات أحدهما الجسيم والآخر نقيضه. ولا يلبثان طويلاً بل يُفني كل منهما الآخر ثانيا (من هنا ظهرت فكرة طاقة الصفر حاول البحث عن أعمال وحياة العالم نيكول تسلى).

ولا يمكن رؤية هذه الجسيمات أو اكتشافها بالكشافّات لان تأثيراتها غير مباشرة ويتنبأ مبدأ الارتياب بوجود أزواج افتراضية متشابهة من جسيمات المادة بحيث يكون أحد الزوجين من المادة والأخر من المادة المضادة. وتخيل هذه الجسيمات على حدود الثقب الأسود أي على حدود أفق الحدث من الممكن جدا أن يسقط الجسم الافتراضي الذي يحمل الطاقة السالبة وينجو الجسم ذو الطاقة الموجبة.

بالنسبة لراصد من بعيد يبدو وكأن الجسيم صادر عن الثقب الأسود ومع دفق الطاقة السالبة إلى داخل الثقب الأسود سوف تنخفض كتلة الثقب الأسود ولفقد الثقب الأسود لبعض كتلته تتضاءل مساحة أفق حدثه فكلما صغرت كتلة الثقب الأسود ارتفعت درجة الحرارة ومع ارتفاع درجة الحرارة يزداد معدل بثه للإشعاع فيتسارع نقصان كتلته أكثر فأكثر ولكن لا أحد يعلم ماذا يحدث للثقب الأسود إذا تقلصت أو انكمشت كتلته إلى درجه كبيرة ولكن الاعتقاد الأقرب أنه سوف ينتهي إلى انفجار نهائي هائل من الإشعاع يعادل انفجار ملايين من القنابل الهيدورجينية. فالثقب الأسود الأولى ذو الكتلة البدائية من ألف مليون طن يكون عمره مقارباً لعمر الكون. أما الثقوب السوداء البدائية ذات الكتلة دون هذه الأرقام فتكون قد تبخرت كليا. وتلك التي لها كتلة أكبر بقليل تستمر في بث إشعاعات على شكل أشعة سينية أشعة غاما وهذه الإشعاعات من سينية وغاما تشبه الموجات الضوئية ولكن بطول موجي أقصر وتكاد هذه الثقوب لا تستحق صفة سوداء فهي حارة في الواقع إلى درجة (الاحمرار - الإبيضاض) وتبث طاقة بمعدل يقارب عشرة آلاف ميغا الواط.

إشعاع هوكينغ

المقالة الرئيسية: إشعاع هوكينغ

طبق عالم الفيزياء النظرية ستيفن هوكينغ نظريات الترموديناميكا والنظرية النسبية العامة وميكانيكا الكم وتوصل إلى أن الثقب الأسود يمكن أن يصدر أشعة. وافترض حدوث إنتاج زوجي عند أفق الحدث للثقب الأسود ينتج عنه إشعاع سُمي «إشعاع هوكينغ». كما استطاع استنتاج أن كتلة الثقب الأسود تتبخر مع الوقت، وقدر عمر تبخر الثقب الأسود بنحو 6710 سنة.

رصد الثقب الأسود

ثقب أسود يمر بين المشاهد ومجرة تقع خلفه، ويرى تشوه ضوء المجرة القادم إلينا (محاكاة تشبيهية)

قد نفتش عن أشعة غاما التي تبثها الثقوب السوداء الأولية طوال حياتها مع إن إشعاعات معظمها سوف تكون ضعيفة بسبب بعدها عنا بعداً كبيراً، ولكن اكتشافها من الممكن. ومن خلال النظر إلي خلفية أشعة غاما لا نجد أي دليل على ثقوب سوداء أولية ولكنها تفيد بأنه لا يمكن تواجد أكثر من 300 منها في كل سنه ضوئية مكعبة من الكون. فلو كان تواجدها مثلاً أكثر بمليون مرة من هذا العدد فإن أقرب ثقب أسود إلينا يبعد ألف مليون كيلومتر، وكي نشاهد ثقبا أسودا أوليا علينا أن نكشف عدة كمات من أشعة غاما صادرة في اتجاه واحد خلال مدى معقول من الزمن كأسبوع مثلا، ولكن نحتاج إلى جهاز استشعار كبير لأشعة غاما وأيضا يجب أن يكون في الفضاء الخارجي لأن الغلاف الجوي للأرض يمتص قدراً كبيراً من أشعة غاما الآتية من خارج الأرض.. إن أكبر مكشاف لأشعة غاما يمكنه التقاطها وتحديد نقطة الثقوب السوداء موجود لدينا هو الطبقة الهوائية للأرض بكاملها. فعندما يصطدم كمٌ عالٍ من الطاقة من أشعة غاما بذرات جو الأرض يـُولد أزواجاً من الإلكترونات والبوزيترونات (نقيض الإلكترون) ونحصل على وابل من الإلكترونات السريعة التي تـُشع ضوءاً يدعى إشعاع شيرنكوف. إن فكرة إشعاع الثقوب السوداء هي من أمثلة التنبؤ الفيزيائي المبني على النظريتين الكبيرتين المـُكتشفتان في هذا القرن : النظرية النسبية العامة وميكانيكا الكم. وهذه أول إشارة إلى أن ميكانيكا الكم قادرة على حل بعض التفردات الثقالية التي تنبأت بها النسبية العامة.

وقد استطاع العلماء الألمان في السنوات القليلة الماضية اكتشاف حقيقة تواجد أحد تلك الثقوب السوداء في مركز المجرة. بالطبع لم يروه رؤية مباشرة، ولكنهم دئبوا على مراقبة حركة نجم كبير قريب من مركز المجرة لمدة سنوات عديدة، ويدور هذا النجم في مدار حول مركز خفي.

وعلى أساس معرفة كتلة النجم ونصف قطر فلكه، استطاع العلماء استنتاج وجود الثقب الأسود في مجرتنا وحساب كتلته التي تبلغ نحو 2 مليون ضعف لكتلة الشمس.

الثقوب السوداء والنظريات الفيزيائية

من المعروف أن قوانين الفيزياء مبنية على النظريات وعلى هذا الأساس بما أنه توجد أجسام تسمى ثقوب سوداء، يمكن للأشياء السقوط فيها بلا عودة فإنه يجب أن تكون هناك أجسام تخرج منها الأشياء تسمى الثقوب البيضاء ومن هنا يمكن للمرء افتراض إمكانية القفز في ثقب أسود في مكان ما ليخرج من ثقب أبيض في مكان آخر. فهذا النوع من السفر الفضائي ممكن نظريا، فهناك حلول لنظرية النسبية العامة يمكن فيها السقوط في ثقب أسود ومن ثم الخروج من ثقب أبيض أيضا لكن الأعمال التالية بينت أن هذه الحلول جميعها غير مستقرة : فالاضطراب الضئيل قد يدمر أخدود الدودة أو المعبر الذي يصل بين الثقب الأسود والثقب الأبيض (أو بين كوننا وكون موازي له)، إن كل هذا الكلام الذي ذُكر يستند إلى حسابات باستخدام النظرية النسبية العامة لأينشتاين وتعتبر هذه الحسابات تقريبية وغير صحيحة تماما لأنها لا تاخذ مبدأ عدم التأكد في الحسبان. اعتبر في الماضي أن الثقب الأسود لا يفقد مادة فهو لا يسمح حتى للضوء بمغادرته، ولكن أعاد ستيفن هوكنغ التفكير ويميل إلى أن بعض الجسيمات يمكنها الانطلاق منه. ولو افترضنا أنه كانت هنالك مركبة فضاء قفزت إلى هذا الثقب ماذا يحدث؟ فيقول ستيفن هوكينغ بناءً على عمل أخير له إن المركبة سوف تذهب إلى كون (طفل) صغير خاص بها كون صغير مكتفٍ ذاتياً يتفرع عن منطقتنا من الكون (الكون الطفل يمكن توضيحه وذلك بأن تتخيل كمية من الزيت في حوض ماء وهي متجمعة حرك هذه الكمية بقلم سوف تنفصل كرة صغيرة من الزيت عن الكرة الكبيرة هذه الكرة الصغيرة هي الكون الطفل والكرة الكبيرة هي عبارة عن كوننا ولاحظ أن الكرة الصغيرة قد ترجع وتتصل مع الكرة الكبيرة) وقد يعود هذا الكون الطفل إلى الانضمام ثانية إلى منطقتنا من عالم الزمكان فإن فعل سيبدو لنا كثقب أسود آخر قد تشكل ثم تبخر والجسيمات التي سقطت في ثقب أسود تبدو كجسيمات مشعة من ثقب آخر. ويبدو هذا وكأنه المطلوب للسماح بالسفر الفضائي عبر الثقوب السوداء لكن هناك عيوباً في هذا المخطط لهذا السفر الكوني أولها أنك لن تستطيع تحديد مكان توجهك أي لا تعلم إلى أين سوف تذهب وأيضا الأكوان الطفلة التي تأخذ الجسيمات التي وقعت في الثقب الأسود تحصل فيما يدعى بالزمن التخيلي يصل رجل الفضاء الذي سقط في الثقب الأسود إلى نهاية بغيضة مؤلمة فهو يستطيل مثل «المعكرونة الاسباجتي» ثم يتمزق بسبب الفرق بين القوى المطبقة على رأسه وقدميه. حتى الجسيمات التي يتكون منها جسمه سوف تنسحق تواريخها في الزمن الحقيقي وستنتهي في متفرد ثقالي. ولكن تواريخها في الزمن التخيلي سوف تستمر حيث تعبر إلى كون طفل ثم تعود للظهور كجسيمات يشعها ثقب أبيض، إن على من يسقط في ثقب أسود أن يتخذ الشعار : (فكر تخيليا). وما نعنيه هو إن الذهاب عبر ثقب أسود ليس مرشحاً ليكون طريقة مرضية وموثوق بها للسفر الكوني لأنها ما زالت في طور الفلسفة النظرية ولربما نتمكن بعد سنوات من الدراسات من دخول الثقب الأسود فبعض العلماء قالو ان الثقب الأسود بوابة لمجرة بعيدة أو عالم آخر

هل يمكن رؤية الثقب الأسود؟

ثقب أسود يجذب إليه المادة من نجم مجاور.

ينشأ الثقب الأسود عندما ينتهي عمر أحد النجوم البالغة الأكبر (حجما) وينتهي وقوده، فينفجر وينهار على نفسه. ويتحول النجم من سحابة كبيرة عظيمة إلى تجمع صغير محدود جداً للمادة المكثفة. ويعمل ذلك التجمع المادي المركز على جذب كل ما حوله من جسيمات أو أي مادة أخرى. وحتى فوتونات الضوء لا تفلت منه بسبب جاذبيته الخارقة، فالثقب الأسود لا ينبعث منه ضوء.

ولكن كل ما ينجذب وينهار على الثقب الأسود يكتسب سرعات عالية جدا وترتفع درجة حرارتها. وتستطيع التلسكوبات الكبيرة على الأرض رؤية تلك الدوامات الشديدة الحرارة. أي أن الثقب الأسود يفصح عن نفسه بواسطة شهيته وجشعه لالتقاط كل مادة حوله. ولا يتعين علينا أن نخاف لأن الفلكيين لم يجدوا أي ثقب أسود بالقرب من المجموعة الشمسية.

أنواع الثقوب السوداء

الثقب الأسود هو المرحلة الأخيرة من عمر نجم عظيم الكتلة. وفي الواقع فهو ليس نجما حيث أنه لا يولّد طاقة عن طريق الاندماج النووي (يتوقف الاندماج النووي في النجم كبير الكتلة بعد استهلاكه لوقوده من الهيدروجين والهيليوم ويصبح ثقبا أسودا لا يشع ضوءا).

ويمكن تكوّن ثقب أسود بعدة طرق:

انظر أيضًا

ملاحظات

  1. ^ The value of cJ/GM2 can exceed 1 for objects other than black holes. The largest value known for a neutron star is ≤ 0.4, and commonly used equations of state would limit that value to < 0.7.[66]
  2. ^ The (outer) event horizon radius scales as: M+M2−(J/M)2−Q2.
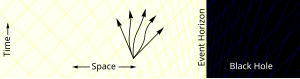
  3. ^ The set of possible paths, or more accurately the future مخروط ضوئي containing all possible خط العالمs (in this diagram the light cone is represented by the V-shaped region bounded by arrows representing light ray world lines), is tilted in this way in Eddington–Finkelstein coordinates (the diagram is a "cartoon" version of an Eddington–Finkelstein coordinate diagram), but in other coordinates the light cones are not tilted in this way, for example in Schwarzschild coordinates they simply narrow without tilting as one approaches the event horizon, and in Kruskal–Szekeres coordinates the light cones do not change shape or orientation at all.[68]
  4. ^ This is true only for 4-dimensional spacetimes. In higher dimensions more complicated horizon topologies like a black ring ‏ are possible.[74][75]

مراجع

  1. ^ أ ب ت Wald 1984
  2. ^ أ ب Wald، R. M. (1997). "Gravitational Collapse and Cosmic Censorship". في Iyer, B. R.؛ Bhawal, B. (المحررون). Black Holes, Gravitational Radiation and the Universe. Springer. ص. 69–86. arXiv:gr-qc/9710068. DOI:10.1007/978-94-017-0934-7. ISBN:978-9401709347.
  3. ^ Overbye، Dennis (8 يونيو 2015). "Black Hole Hunters". ناسا. مؤرشف من الأصل في 2015-06-09. اطلع عليه بتاريخ 2015-06-08.
  4. ^ "Introduction to Black Holes". مؤرشف من الأصل في 2020-03-20. اطلع عليه بتاريخ 2017-09-26.
  5. ^ Schutz، Bernard F. (2003). Gravity from the ground up. Cambridge University Press. ص. 110. ISBN:978-0-521-45506-0. مؤرشف من الأصل في 2016-12-02.
  6. ^ Davies، P. C. W. (1978). "Thermodynamics of Black Holes" (PDF). Reports on Progress in Physics. ج. 41 ع. 8: 1313–1355. Bibcode:1978RPPh...41.1313D. DOI:10.1088/0034-4885/41/8/004. مؤرشف من الأصل (PDF) في 2013-05-10.
  7. ^ أ ب ت Montgomery، Colin؛ Orchiston، Wayne؛ Whittingham، Ian (2009). "Michell, Laplace and the origin of the black hole concept". Journal of Astronomical History and Heritage. ج. 12 ع. 2: 90–96. Bibcode:2009JAHH...12...90M.
  8. ^ أ ب ت ث Abbott, B.P.؛ وآخرون (2016). "Observation of Gravitational Waves from a Binary Black Hole Merger". Phys. Rev. Lett. ج. 116 ع. 6: 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. DOI:10.1103/PhysRevLett.116.061102. PMID:26918975.
  9. ^ Siegel، Ethan. "Five Surprising Truths About Black Holes From LIGO". Forbes. مؤرشف من الأصل في 2019-04-10. اطلع عليه بتاريخ 2019-04-12.
  10. ^ أ ب "Detection of gravitational waves". ليغو (مرصد). مؤرشف من الأصل في 2019-03-22. اطلع عليه بتاريخ 2018-04-09.
  11. ^ Event Horizon Telescope، The (2019). "First M87 Event Horizon Telescope Results. I. The Shadow of the Supermassive Black Hole". المجلة الفيزيائية الفلكية. ج. 87 ع. 1. DOI:10.3847/2041-8213/ab0ec7.
  12. ^ Bouman، Katherine L.؛ Johnson، Michael D.؛ Zoran، Daniel؛ Fish، Vincent L.؛ Doeleman، Sheperd S.؛ Freeman، William T. (2016). "Computational Imaging for VLBI Image Reconstruction": 913–922. arXiv:1512.01413. DOI:10.1109/CVPR.2016.105. مؤرشف من الأصل في 2019-04-11. {{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب |دورية محكمة= (مساعدة)
  13. ^ Michell، J. (1784). "On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose. By the Rev. John Michell, B. D. F. R. S. In a Letter to Henry Cavendish, Esq. F. R. S. and A. S". المعاملات الفلسفية للجمعية الملكية. ج. 74: 35–57. Bibcode:1784RSPT...74...35M. DOI:10.1098/rstl.1784.0008. JSTOR:106576.
  14. ^ أ ب Thorne 1994
  15. ^ Slayter، Elizabeth M.؛ Slayter، Henry S. (1992). Light and Electron Microscopy. Cambridge University Press. ISBN:978-0-521-33948-3. مؤرشف من الأصل في 2017-11-30.
  16. ^ Crass، Institute of Astronomy – Design by D.R. Wilkins and S.J. "Light escaping from black holes". www.ast.cam.ac.uk. مؤرشف من الأصل في 2018-07-01. اطلع عليه بتاريخ 2018-03-10.
  17. ^ أ ب Schwarzschild، K. (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsberichte der Königlich Preussischen Akademie der Wissenschaften. ج. 7: 189–196. مؤرشف من الأصل في 2019-05-02.
  18. ^ Droste، J. (1917). "On the field of a single centre in Einstein's theory of gravitation, and the motion of a particle in that field" (pdf). Proceedings Royal Academy Amsterdam. ج. 19 ع. 1: 197–215. مؤرشف (PDF) من الأصل في 2013-05-18.
  19. ^ Kox، A. J. (1992). "General Relativity in the Netherlands: 1915–1920". في Eisenstaedt، Jean؛ Kox، A. J. (المحررون). Studies in the history of general relativity. Birkhäuser. ص. 41. ISBN:978-0-8176-3479-7.
  20. ^ 't Hooft، G. (2009). "Introduction to the Theory of Black Holes" (pdf). Institute for Theoretical Physics / Spinoza Institute: 47–48. مؤرشف (PDF) من الأصل في 2009-05-21.
  21. ^ Eddington، Arthur (1926). The Internal Constitution of the Stars. Cambridge University Press. ص. 6. ISBN:9780521337083. مؤرشف من الأصل في 2016-08-11.
  22. ^ Thorne، Kip S.؛ Hawking، Stephen (1994). Black Holes and Time Warps: Einstein's Outrageous Legacy. W. W. Norton & Company. ص. 134–135. ISBN:9780393312768. مؤرشف من الأصل في 2020-01-02. اطلع عليه بتاريخ 2019-04-12. The first conclusion was the Newtonian version of light not escaping; the second was a semi-accurate, relativistic description; and the third was typical Eddingtonian hyperbole ... when a star is as small as the critical circumference, the curvature is strong but not infinite, and space is definitely not wrapped around the star. Eddington may have known this, but his description made a good story, and it captured in a whimsical way the spirit of Schwarzschild's spacetime curvature."
  23. ^ Venkataraman، G. (1992). Chandrasekhar and his limit. Universities Press. ص. 89. ISBN:978-81-7371-035-3. مؤرشف من الأصل في 2016-08-11.
  24. ^ Detweiler، S. (1981). "Resource letter BH-1: Black holes". المجلة الأمريكية للفيزياء. ج. 49 ع. 5: 394–400. Bibcode:1981AmJPh..49..394D. DOI:10.1119/1.12686.
  25. ^ Harpaz، A. (1994). Stellar evolution. A K Peters ‏. ص. 105. ISBN:978-1-56881-012-6. مؤرشف من الأصل في 2016-08-11.{{استشهاد بكتاب}}: صيانة الاستشهاد: علامات ترقيم زائدة (link)
  26. ^ أ ب Oppenheimer، J. R.؛ Volkoff، G. M. (1939). "On Massive Neutron Cores". فيزيكال ريفيو. ج. 55 ع. 4: 374–381. Bibcode:1939PhRv...55..374O. DOI:10.1103/PhysRev.55.374.
  27. ^ Bombaci، I. (1996). "The Maximum Mass of a Neutron Star". مجلة علم الفلك والفيزياء الفلكية. ج. 305: 871–877. Bibcode:1996A&A...305..871B.
  28. ^ Cho، A. (16 فبراير 2018). "A weight limit emerges for neutron stars". Science. ج. 359 ع. 6377: 724–725. Bibcode:2018Sci...359..724C. DOI:10.1126/science.359.6377.724. PMID:29449468. مؤرشف من الأصل في 2019-11-06. اطلع عليه بتاريخ 2018-02-16.
  29. ^ Margalit، B.؛ Metzger، B. D. (1 ديسمبر 2017). "Constraining the Maximum Mass of Neutron Stars from Multi-messenger Observations of GW170817". The Astrophysical Journal. ج. 850 ع. 2: L19. arXiv:1710.05938. Bibcode:2017ApJ...850L..19M. DOI:10.3847/2041-8213/aa991c.
  30. ^ Shibata، M.؛ Fujibayashi، S.؛ Hotokezaka، K.؛ Kiuchi، K.؛ Kyutoku، K.؛ Sekiguchi، Y.؛ Tanaka، M. (22 ديسمبر 2017). "Modeling GW170817 based on numerical relativity and its implications". Physical Review D. ج. 96 ع. 12: 123012. arXiv:1710.07579. Bibcode:2017PhRvD..96l3012S. DOI:10.1103/PhysRevD.96.123012.
  31. ^ Ruiz، M.؛ Shapiro، S. L.؛ Tsokaros، A. (11 يناير 2018). "GW170817, general relativistic magnetohydrodynamic simulations, and the neutron star maximum mass". Physical Review D. ج. 97 ع. 2: 021501. arXiv:1711.00473. Bibcode:2018PhRvD..97b1501R. DOI:10.1103/PhysRevD.97.021501. PMID:30003183. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)
  32. ^ Rezzolla، L.؛ Most، E. R.؛ Weih، L. R. (9 يناير 2018). "Using Gravitational-wave Observations and Quasi-universal Relations to Constrain the Maximum Mass of Neutron Stars". Astrophysical Journal. ج. 852 ع. 2: L25. arXiv:1711.00314. Bibcode:2018ApJ...852L..25R. DOI:10.3847/2041-8213/aaa401.
  33. ^ Ruffini، R.؛ Wheeler، J. A. (1971). "Introducing the black hole" (PDF). Physics Today. ج. 24 ع. 1: 30–41. Bibcode:1971PhT....24a..30R. DOI:10.1063/1.3022513. مؤرشف (PDF) من الأصل في 2011-07-25.
  34. ^ Finkelstein، D. (1958). "Past-Future Asymmetry of the Gravitational Field of a Point Particle". فيزيكال ريفيو. ج. 110 ع. 4: 965–967. Bibcode:1958PhRv..110..965F. DOI:10.1103/PhysRev.110.965.
  35. ^ Kruskal، M. (1960). "Maximal Extension of Schwarzschild Metric". فيزيكال ريفيو. ج. 119 ع. 5: 1743. Bibcode:1960PhRv..119.1743K. DOI:10.1103/PhysRev.119.1743.
  36. ^ Hewish، A.؛ وآخرون (1968). "Observation of a Rapidly Pulsating Radio Source". نيتشر (مجلة). ج. 217 ع. 5130: 709–713. Bibcode:1968Natur.217..709H. DOI:10.1038/217709a0.
  37. ^ Pilkington، J. D. H.؛ وآخرون (1968). "Observations of some further Pulsed Radio Sources". نيتشر (مجلة). ج. 218 ع. 5137: 126–129. Bibcode:1968Natur.218..126P. DOI:10.1038/218126a0.
  38. ^ Hewish، A. (1970). "Pulsars". Annual Review of Astronomy and Astrophysics. ج. 8 ع. 1: 265–296. Bibcode:1970ARA&A...8..265H. DOI:10.1146/annurev.aa.08.090170.001405.
  39. ^ Newman، E. T.؛ وآخرون (1965). "Metric of a Rotating, Charged Mass". Journal of Mathematical Physics. ج. 6 ع. 6: 918. Bibcode:1965JMP.....6..918N. DOI:10.1063/1.1704351.
  40. ^ Israel، W. (1967). "Event Horizons in Static Vacuum Space-Times". فيزيكال ريفيو. ج. 164 ع. 5: 1776. Bibcode:1967PhRv..164.1776I. DOI:10.1103/PhysRev.164.1776.
  41. ^ Carter، B. (1971). "Axisymmetric Black Hole Has Only Two Degrees of Freedom". Physical Review Letters. ج. 26 ع. 6: 331. Bibcode:1971PhRvL..26..331C. DOI:10.1103/PhysRevLett.26.331.
  42. ^ Carter، B. (1977). "The vacuum black hole uniqueness theorem and its conceivable generalisations". Proceedings of the 1st Marcel Grossmann meeting on general relativity. ص. 243–254.
  43. ^ Robinson، D. (1975). "Uniqueness of the Kerr Black Hole". Physical Review Letters. ج. 34 ع. 14: 905. Bibcode:1975PhRvL..34..905R. DOI:10.1103/PhysRevLett.34.905.
  44. ^ أ ب Heusler، M. (2012). "Stationary Black Holes: Uniqueness and Beyond". Living Reviews in Relativity. ج. 15 ع. 7: 7. arXiv:1205.6112. Bibcode:2012LRR....15....7C. DOI:10.12942/lrr-2012-7. PMID:28179837. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)
  45. ^ أ ب Penrose، R. (1965). "Gravitational Collapse and Space-Time Singularities". Physical Review Letters. ج. 14 ع. 3: 57. Bibcode:1965PhRvL..14...57P. DOI:10.1103/PhysRevLett.14.57.
  46. ^ Ford، L. H. (2003). "The Classical Singularity Theorems and Their Quantum Loopholes". International Journal of Theoretical Physics. ج. 42 ع. 6: 1219. DOI:10.1023/A:1025754515197.
  47. ^ Bardeen، J. M.؛ Carter، B.؛ Hawking، S. W. (1973). "The four laws of black hole mechanics". Communications in Mathematical Physics. ج. 31 ع. 2: 161–170. Bibcode:1973CMaPh..31..161B. DOI:10.1007/BF01645742. MR:0334798. Zbl:1125.83309.
  48. ^ أ ب ت Hawking، S. W. (1974). "Black hole explosions?". Nature. ج. 248 ع. 5443: 30–31. Bibcode:1974Natur.248...30H. DOI:10.1038/248030a0.
  49. ^ Popova، Maria (27 يونيو 2016). "Mapping the Heavens: How Cosmology Shaped Our Understanding of the Universe and the Strange Story of How the Term "Black Hole" Was Born". brainpickings.org. مؤرشف من الأصل في 2019-04-19. اطلع عليه بتاريخ 2019-04-12.
  50. ^ أ ب "MIT's Marcia Bartusiak On Understanding Our Place In The Universe". www.wbur.org. مؤرشف من الأصل في 2019-04-12. اطلع عليه بتاريخ 2019-04-12.
  51. ^ أ ب Siegfried، Tom (23 ديسمبر 2013). "50 years later, it's hard to say who named black holes". Science News. مؤرشف من الأصل في 2017-03-09. اطلع عليه بتاريخ 2017-09-24. It seems that the "black hole" label was also bandied about in January 1964 in Cleveland at a meeting of the American Association for the Advancement of Science. Science News Letter reporter Ann Ewing reported from that meeting, describing how an intense gravitational field could cause a star to collapse in on itself. "Such a star then forms a 'black hole' in the universe," Ewing wrote
  52. ^ Brown، Emma (3 أغسطس 2010). "Ann E. Ewing, journalist first reported black holes". Boston.com. مؤرشف من الأصل في 2017-09-24. اطلع عليه بتاريخ 2017-09-24.
  53. ^ "Pioneering Physicist John Wheeler Dies at 96". ساينتفك أمريكان. مؤرشف من الأصل في 2016-11-28. اطلع عليه بتاريخ 2016-11-27.
  54. ^ Overbye، Dennis (14 أبريل 2008). "John A. Wheeler, Physicist Who Coined the Term 'Black Hole,' Is Dead at 96". نيويورك تايمز. مؤرشف من الأصل في 2016-11-22. اطلع عليه بتاريخ 2016-11-27.
  55. ^ أ ب ت ث ج ح خ د ذ ر ز س ش ص ض ط Carroll 2004
  56. ^ Thorne، K. S.؛ Price، R. H. (1986). Black holes: the membrane paradigm. Yale University Press. ISBN:978-0-300-03770-8.
  57. ^ Anderson، Warren G. (1996). "The Black Hole Information Loss Problem". الولايات المتحدةenet Physics FAQ. مؤرشف من الأصل في 2009-01-22. اطلع عليه بتاريخ 2009-03-24.
  58. ^ {{استشهاد بمنشورات مؤتمر}}: استشهاد فارغ! (مساعدة)
  59. ^ Hawking & Ellis 1973
  60. ^ Seeds، Michael A.؛ Backman، Dana E. (2007). Perspectives on Astronomy. Cengage Learning. ص. 167. ISBN:978-0-495-11352-2. مؤرشف من الأصل في 2016-08-10.
  61. ^ Shapiro، S. L.؛ Teukolsky، S. A. (1983). Black holes, white dwarfs, and neutron stars: the physics of compact objects. John Wiley and Sons. ص. 357. ISBN:978-0-471-87316-7.
  62. ^ Berger، B. K. (2002). "Numerical Approaches to Spacetime Singularities". Living Reviews in Relativity. ج. 5 ع. 1: 2002–1. arXiv:gr-qc/0201056. Bibcode:2002LRR.....5....1B. DOI:10.12942/lrr-2002-1. PMID:28179859. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)
  63. ^ McClintock، J. E.؛ Shafee، R.؛ Narayan، R.؛ Remillard، R. A.؛ Davis، S. W.؛ Li، L.-X. (2006). "The Spin of the Near-Extreme Kerr Black Hole GRS 1915+105". Astrophysical Journal. ج. 652 ع. 1: 518–539. arXiv:astro-ph/0606076. Bibcode:2006ApJ...652..518M. DOI:10.1086/508457.
  64. ^ أ ب Abbott، B. P. (1 يونيو 2017). "GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2". Physical Review Letters. ج. 118 ع. 22: 221101. arXiv:1706.01812. Bibcode:2017PhRvL.118v1101A. DOI:10.1103/PhysRevLett.118.221101. PMID:28621973.
  65. ^ Abbott، B. P.؛ وآخرون (LIGO Scientific Collaboration and مقياس التداخل فيرجو) (1 يونيو 2017). "GW170104: Observation of a 50-Solar-Mass Binary Black Hole Coalescence at Redshift 0.2". Physical Review Letters. ج. 118 ع. 22: 221101. arXiv:1706.01812. Bibcode:2017PhRvL.118v1101A. DOI:10.1103/PhysRevLett.118.221101. PMID:28621973.
  66. ^ Abbott، B. P.؛ وآخرون (LIGO Scientific Collaboration & مقياس التداخل فيرجو) (16 أكتوبر 2017). "GW170817: Observation of Gravitational Waves from a Binary Neutron Star Inspiral". Physical Review Letters. ج. 119 ع. 16: 161101. arXiv:1710.05832. Bibcode:2017PhRvL.119p1101A. DOI:10.1103/PhysRevLett.119.161101. PMID:29099225.
  67. ^ Saa، Alberto؛ Santarelli، Raphael (18 يوليو 2011). "Destroying a near-extremal Kerr–Newman black hole". Physical Review D. ج. 84 ع. 2: 027501. arXiv:1105.3950. Bibcode:2011PhRvD..84b7501S. DOI:10.1103/PhysRevD.84.027501.
  68. ^ Thorne, Misner & Wheeler 1973، صفحة 848
  69. ^ Wheeler 2007
  70. ^ "Singularities and Black Holes > Lightcones and Causal Structure". plato.stanford.edu. موسوعة ستانفورد للفلسفة. مؤرشف من الأصل في 2019-05-17. اطلع عليه بتاريخ 2018-03-11.
  71. ^ "Inside a black hole". Knowing the universe and its secrets. مؤرشف من الأصل في 2009-04-23. اطلع عليه بتاريخ 2009-03-26.
  72. ^ "What happens to you if you fall into a black holes". math.ucr.edu. جون سي بايز. مؤرشف من الأصل في 2019-02-13. اطلع عليه بتاريخ 2018-03-11.
  73. ^ "Watch: Three Ways an Astronaut Could Fall Into a Black Hole". 1 فبراير 2014. مؤرشف من الأصل في 2019-04-15. اطلع عليه بتاريخ 2018-03-13.
  74. ^ Emparan، R.؛ Reall، H. S. (2008). "Black Holes in Higher Dimensions". Living Reviews in Relativity. ج. 11 ع. 6: 6. arXiv:0801.3471. Bibcode:2008LRR....11....6E. DOI:10.12942/lrr-2008-6. PMC:5253845. PMID:28163607.
  75. ^ Obers، N. A. (2009). Papantonopoulos، Eleftherios (المحرر). Black Holes in Higher-Dimensional Gravity (PDF). ص. 211–258. arXiv:0802.0519. Bibcode:2009LNP...769.....P. DOI:10.1007/978-3-540-88460-6. ISBN:978-3-540-88459-0. مؤرشف من الأصل (PDF) في 2018-07-26. {{استشهاد بكتاب}}: |صحيفة= تُجوهل (مساعدة)
  76. ^ hawking & ellis 1973
  77. ^ Shapiro، Stuart (1995). "Toroidal black holes and topological censorship". Physical Review D. ج. 52 ع. 12.
  78. ^ "Sizes of Black Holes? How Big is a Black Hole?". Sky & Telescope. 22 يوليو 2014. مؤرشف من الأصل في 2019-04-03. اطلع عليه بتاريخ 2018-10-09.
  79. ^ Lewis، G. F.؛ Kwan، J. (2007). "No Way Back: Maximizing Survival Time Below the Schwarzschild Event Horizon". Publications of the Astronomical Society of Australia. ج. 24 ع. 2: 46–52. arXiv:0705.1029. Bibcode:2007PASA...24...46L. DOI:10.1071/AS07012.
  80. ^ أ ب Heusler، M. (2012). "Stationary Black Holes: Uniqueness and Beyond". Living Reviews in Relativity. ج. 15 ع. 7: 7. arXiv:1205.6112. Bibcode:2012LRR....15....7C. DOI:10.12942/lrr-2012-7.
  81. ^ Droz، S.؛ Israel، W.؛ Morsink، S. M. (1996). "Black holes: the inside story". Physics World. ج. 9 ع. 1: 34–37. Bibcode:1996PhyW....9...34D. مؤرشف من الأصل في 2014-08-17.
  82. ^ Poisson، E.؛ Israel، W. (1990). "Internal structure of black holes". Physical Review D. ج. 41 ع. 6: 1796. Bibcode:1990PhRvD..41.1796P. DOI:10.1103/PhysRevD.41.1796.
  83. ^ Hamade، R. (1996). "Black Holes and Quantum Gravity". Cambridge Relativity and Cosmology. University of Cambridge. مؤرشف من الأصل في 2009-04-07. اطلع عليه بتاريخ 2009-03-26.
  84. ^ Palmer، D. "Ask an Astrophysicist: Quantum Gravity and Black Holes". NASA. مؤرشف من الأصل في 2009-03-28. اطلع عليه بتاريخ 2009-03-26.
  85. ^ أ ب Nitta، Daisuke؛ Chiba، Takeshi؛ Sugiyama، Naoshi (سبتمبر 2011). "Shadows of colliding black holes". Physical Review D. ج. 84 ع. 6: 063008. arXiv:1106.2425. Bibcode:2011PhRvD..84f3008N. DOI:10.1103/PhysRevD.84.063008.
  86. ^ أ ب Visser. "The Kerr spacetime: A brief introduction". arXiv:0706.0622., page 35, Fig. 3 نسخة محفوظة 18 أكتوبر 2019 على موقع واي باك مشين.
  87. ^ Thorne, Misner & Wheeler 1973
  88. ^ Bardeen، J. M. (1972). "Rotating black holes: locally nonrotating frames, energy extraction, and scalar synchrotron radiation". The Astrophysical Journal. ج. 178: 347–370. Bibcode:1972ApJ...178..347B. DOI:10.1086/151796.
  89. ^ Einstein، A. (1939). "On A Stationary System With Spherical Symmetry Consisting of Many Gravitating Masses". Annals of Mathematics. ج. 40 ع. 4: 922–936. DOI:10.2307/1968902. JSTOR:1968902. مؤرشف من الأصل في 2022-04-10.
  90. ^ Kerr، R. P. (2009). "The Kerr and Kerr-Schild metrics". في Wiltshire، D. L.؛ Visser، M.؛ Scott، S. M. (المحررون). The Kerr Spacetime. Cambridge University Press. arXiv:0706.1109. Bibcode:2007arXiv0706.1109K. ISBN:978-0-521-88512-6.
  91. ^ Hawking، S. W.؛ Penrose، R. (يناير 1970). "The Singularities of Gravitational Collapse and Cosmology". وقائع الجمعية الملكية. ج. 314 ع. 1519: 529–548. Bibcode:1970RSPSA.314..529H. DOI:10.1098/rspa.1970.0021. JSTOR:2416467.
  92. ^ أ ب ت Pacucci، F.؛ Ferrara، A.؛ Grazian، A.؛ Fiore، F.؛ Giallongo، E. (2016). "First Identification of Direct Collapse Black Hole Candidates in the Early Universe in CANDELS/GOODS-S". Mon. Not. R. Astron. Soc. ج. 459 ع. 2: 1432. arXiv:1603.08522. Bibcode:2016MNRAS.459.1432P. DOI:10.1093/mnras/stw725.
  93. ^ أ ب Carr، B. J. (2005). "Primordial Black Holes: Do They Exist and Are They Useful?". في Suzuki، H.؛ Yokoyama، J.؛ Suto، Y.؛ Sato، K. (المحررون). Inflating Horizon of Particle Astrophysics and Cosmology. Universal Academy Press. ص. astro–ph/0511743. arXiv:astro-ph/0511743. Bibcode:2005astro.ph.11743C. ISBN:978-4-946443-94-7.
  94. ^ Griffiths، Martin (2012). Planetary Nebulae and How to Observe Them (ط. illustrated). Springer Science & Business Media. ص. 11. ISBN:978-1-4614-1781-1. مؤرشف من الأصل في 2016-12-03. Extract of page 11
  95. ^ "Artist's impression of supermassive black hole seed". مؤرشف من الأصل في 2016-05-30. اطلع عليه بتاريخ 2016-05-27.
  96. ^ أ ب ت Rees، M. J.؛ Volonteri، M. (2007). "Massive black holes: formation and evolution". في Karas، V.؛ Matt، G. (المحررون). Black Holes from Stars to Galaxies – Across the Range of Masses. ص. 51–58. arXiv:astro-ph/0701512. Bibcode:2007IAUS..238...51R. DOI:10.1017/S1743921307004681. ISBN:978-0-521-86347-6. {{استشهاد بكتاب}}: |عمل= تُجوهل (مساعدة)
  97. ^ Penrose، R. (2002). "Gravitational Collapse: The Role of General Relativity" (PDF). General Relativity and Gravitation. ج. 34 ع. 7: 1141. Bibcode:2002GReGr..34.1141P. DOI:10.1023/A:1016578408204. مؤرشف من الأصل (PDF) في 2013-05-26.
  98. ^ Philip Gibbs. "Is the Big Bang a black hole?". جون سي بايز. مؤرشف من الأصل في 2018-12-31. اطلع عليه بتاريخ 2018-03-16.
  99. ^ Giddings، S. B.؛ Thomas، S. (2002). "High energy colliders as black hole factories: The end of short distance physics". Physical Review D. ج. 65 ع. 5: 056010. arXiv:hep-ph/0106219. Bibcode:2002PhRvD..65e6010G. DOI:10.1103/PhysRevD.65.056010.
  100. ^ Harada، T. (2006). "Is there a black hole minimum mass?". Physical Review D. ج. 74 ع. 8: 084004. arXiv:gr-qc/0609055. Bibcode:2006PhRvD..74h4004H. DOI:10.1103/PhysRevD.74.084004.
  101. ^ Arkani–Hamed، N.؛ Dimopoulos، S.؛ Dvali، G. (1998). "The hierarchy problem and new dimensions at a millimeter". Physics Letters B. ج. 429 ع. 3–4: 263–272. arXiv:hep-ph/9803315. Bibcode:1998PhLB..429..263A. DOI:10.1016/S0370-2693(98)00466-3.
  102. ^ LHC Safety Assessment Group. "Review of the Safety of LHC Collisions" (PDF). CERN. مؤرشف (PDF) من الأصل في 2010-04-14.
  103. ^ Cavaglià، M. (2010). "Particle accelerators as black hole factories?". Einstein-Online. ج. 4: 1010. مؤرشف من الأصل في 2013-05-08.
  104. ^ Vesperini، E.؛ McMillan، S. L. W.؛ d'Ercole، A.؛ وآخرون (2010). "Intermediate-Mass Black Holes in Early Globular Clusters". The Astrophysical Journal Letters. ج. 713 ع. 1: L41–L44. arXiv:1003.3470. Bibcode:2010ApJ...713L..41V. DOI:10.1088/2041-8205/713/1/L41.
  105. ^ Zwart، S. F. P.؛ Baumgardt، H.؛ Hut، P.؛ وآخرون (2004). "Formation of massive black holes through runaway collisions in dense young star clusters". Nature. ج. 428 ع. 6984: 724–726. arXiv:astro-ph/0402622. Bibcode:2004Natur.428..724P. DOI:10.1038/nature02448. PMID:15085124.
  106. ^ O'Leary، R. M.؛ Rasio، F. A.؛ Fregeau، J. M.؛ وآخرون (2006). "Binary Mergers and Growth of Black Holes in Dense Star Clusters". The Astrophysical Journal. ج. 637 ع. 2: 937–951. arXiv:astro-ph/0508224. Bibcode:2006ApJ...637..937O. DOI:10.1086/498446.
  107. ^ Page، D. N. (2005). "Hawking radiation and black hole thermodynamics". New Journal of Physics. ج. 7 ع. 1: 203. arXiv:hep-th/0409024. Bibcode:2005NJPh....7..203P. DOI:10.1088/1367-2630/7/1/203.
  108. ^ Siegel، Ethan (2017). "Ask Ethan: Do Black Holes Grow Faster Than They Evaporate?". Forbes ("Starts With A Bang" blog). مؤرشف من الأصل في 2018-11-22. اطلع عليه بتاريخ 2018-03-17.
  109. ^ Sivaram، C. (2001). "Black hole Hawking radiation may never be observed!". General Relativity and Gravitation. ج. 33 ع. 2: 175–181. Bibcode:2001GReGr..33..175S. DOI:10.1023/A:1002753400430.
  110. ^ "Evaporating black holes?". Einstein online. Max Planck Institute for Gravitational Physics. 2010. مؤرشف من الأصل في 2011-07-22. اطلع عليه بتاريخ 2010-12-12.
  111. ^ Giddings، S. B.؛ Mangano، M. L. (2008). "Astrophysical implications of hypothetical stable TeV-scale black holes". Physical Review D. ج. 78 ع. 3: 035009. arXiv:0806.3381. Bibcode:2008PhRvD..78c5009G. DOI:10.1103/PhysRevD.78.035009.
  112. ^ Peskin، M. E. (2008). "The end of the world at the Large Hadron Collider?". Physics. ج. 1: 14. Bibcode:2008PhyOJ...1...14P. DOI:10.1103/Physics.1.14.
  113. ^ Fichtel، C. E.؛ Bertsch، D. L.؛ Dingus، B. L.؛ وآخرون (1994). "Search of the energetic gamma-ray experiment telescope (EGRET) data for high-energy gamma-ray microsecond bursts". Astrophysical Journal. ج. 434 ع. 2: 557–559. Bibcode:1994ApJ...434..557F. DOI:10.1086/174758.
  114. ^ Naeye، R. "Testing Fundamental Physics". NASA. مؤرشف من الأصل في 2008-08-31. اطلع عليه بتاريخ 2008-09-16.
  115. ^ أ ب Frautschi، S. (1982). "Entropy in an Expanding Universe". Science. ج. 217 ع. 4560: 593–599. Bibcode:1982Sci...217..593F. DOI:10.1126/science.217.4560.593. PMID:17817517. See page 596: table 1 and section "black hole decay" and previous sentence on that page.
  116. ^ Particle emission rates from a black hole: Massless particles from an uncharged, nonrotating hole, Don N. Page, Physical Review D 13 (1976), pp. 198–206. دُوِي:10.1103/PhysRevD.13.198. See in particular equation (27).
  117. ^ "Black Holes | Science Mission Directorate". NASA. مؤرشف من الأصل في 2019-05-18. اطلع عليه بتاريخ 2018-03-17.
  118. ^ "April 2017 Observations". Event Horizon Telescope. مؤرشف من الأصل في 2019-04-10. اطلع عليه بتاريخ 2019-04-11.
  119. ^ Overbye، Dennis (10 أبريل 2019). "Darkness Visible, Finally: Astronomers Capture First Ever Image of a Black Hole". The New York Times. مؤرشف من الأصل في 2019-05-21. اطلع عليه بتاريخ 2019-04-11.
  120. ^ AP (10 أبريل 2019). "Astronomers Reveal the First Picture of a Black Hole". The New York Times (video). مؤرشف من الأصل في 2019-05-22. اطلع عليه بتاريخ 2019-04-11.
  121. ^ Doeleman، Shep (4 أبريل 2016). "The Event Horizon Telescope: Imaging and Time-Resolving a Black Hole". Physics @ Berkeley. مؤرشف من الأصل في 2016-12-01. اطلع عليه بتاريخ 2016-07-08.
  122. ^ أ ب Grossman، Lisa؛ Conover، Emily (10 أبريل 2019). "The first picture of a black hole opens a new era of astrophysics". Science News. مؤرشف من الأصل في 2019-04-27. اطلع عليه بتاريخ 2019-04-11.
  123. ^ Johnson، M. D.؛ Fish، V. L.؛ Doeleman، S. S.؛ Marrone، D. P.؛ Plambeck، R. L.؛ Wardle، J. F. C.؛ Akiyama، K.؛ Asada، K.؛ Beaudoin، C. (4 ديسمبر 2015). "Resolved magnetic-field structure and variability near the event horizon of Sagittarius A*". Science. ج. 350 ع. 6265: 1242–1245. arXiv:1512.01220. Bibcode:2015Sci...350.1242J. DOI:10.1126/science.aac7087. PMID:26785487. مؤرشف من الأصل في 2015-12-06.
  124. ^ "Event Horizon Telescope Reveals Magnetic Fields at Milky Way's Central Black Hole". cfa.harvard.edu. 3 ديسمبر 2015. مؤرشف من الأصل في 2015-12-31. اطلع عليه بتاريخ 2016-01-12.
  125. ^ O. Straub ، FH Vincent ، MA Abramowicz ، E. Gourgoulhon ، T. Paumard ، "نمذجة صورة ظلية ثقب أسود في Sgr A * مع ion tori" ، Astron Astroph 543 (2012) A8
  126. ^ Overbye، Dennis (11 فبراير 2016). "Physicists Detect Gravitational Waves, Proving Einstein Right". نيويورك تايمز. مؤرشف من الأصل في 2016-02-11. اطلع عليه بتاريخ 2016-02-11.
  127. ^ Abbott، Benjamin P. (11 فبراير 2016). "Properties of the binary black hole merger GW150914". Physical Review Letters. ج. 116 ع. 24: 241102. arXiv:1602.03840. Bibcode:2016PhRvL.116x1102A. DOI:10.1103/PhysRevLett.116.241102. PMID:27367378.
  128. ^ أ ب Cardoso, V.؛ Franzin, E.؛ Pani, P. (2016). "Is the gravitational-wave ringdown a probe of the event horizon?". Physical Review Letters. ج. 116 ع. 17: 171101. arXiv:1602.07309. Bibcode:2016PhRvL.116q1101C. DOI:10.1103/PhysRevLett.116.171101. PMID:27176511.
  129. ^ Abbott، Benjamin P. (11 فبراير 2016). "Tests of general relativity with GW150914". ليغو (مرصد). مؤرشف من الأصل في 2016-02-15. اطلع عليه بتاريخ 2016-02-12.
  130. ^ Abbott، B. P. (2016). "Astrophysical Implications of the Binary Black Hole Merger GW150914". Astrophys. J. Lett. ج. 818 ع. 2: L22. arXiv:1602.03846. Bibcode:2016ApJ...818L..22A. DOI:10.3847/2041-8205/818/2/L22. مؤرشف من الأصل في 2016-03-16.
  131. ^ Overbye، Dennis (15 يونيو 2016). "Scientists Hear a Second Chirp From Colliding Black Holes". نيويورك تايمز. مؤرشف من الأصل في 2016-06-15. اطلع عليه بتاريخ 2016-06-15.
  132. ^ أ ب Gillessen، S.؛ Eisenhauer، F.؛ Trippe، S.؛ وآخرون (2009). "Monitoring Stellar Orbits around the Massive Black Hole in the Galactic Center". The Astrophysical Journal. ج. 692 ع. 2: 1075–1109. arXiv:0810.4674. Bibcode:2009ApJ...692.1075G. DOI:10.1088/0004-637X/692/2/1075.
  133. ^ أ ب Ghez، A. M.؛ Klein، B. L.؛ Morris، M.؛ وآخرون (1998). "High Proper‐Motion Stars in the Vicinity of Sagittarius A*: Evidence for a Supermassive Black Hole at the Center of Our Galaxy". The Astrophysical Journal. ج. 509 ع. 2: 678–686. arXiv:astro-ph/9807210. Bibcode:1998ApJ...509..678G. DOI:10.1086/306528.
  134. ^ Broderick، Avery؛ Loeb، Abraham؛ Narayan، Ramesh (أغسطس 2009). "The Event Horizon of Sagittarius A*". The Astrophysical Journal. ج. 701 ع. 2: 1357–1366. arXiv:0903.1105. Bibcode:2009ApJ...701.1357B. DOI:10.1088/0004-637X/701/2/1357.
  135. ^ أ ب "NASA's NuSTAR Sees Rare Blurring of Black Hole Light". ناسا. 12 أغسطس 2014. مؤرشف من الأصل في 2014-08-13. اطلع عليه بتاريخ 2014-08-12.
  136. ^ "Researchers clarify dynamics of black hole rotational energy". مؤرشف من الأصل في 2018-09-17. اطلع عليه بتاريخ 2018-09-17.
  137. ^ Marck، Jean-Alain (1 مارس 1996). "Short-cut method of solution of geodesic equations for Schwarzchild black hole". Classical and Quantum Gravity. ج. 13 ع. 3: 393–402. arXiv:gr-qc/9505010. DOI:10.1088/0264-9381/13/3/007. ISSN:0264-9381.
  138. ^ أ ب McClintock، J. E.؛ Remillard، R. A. (2006). "Black Hole Binaries". في Lewin، W.؛ van der Klis، M. (المحررون). Compact Stellar X-ray Sources. ص. 157. arXiv:astro-ph/0306213. Bibcode:2006csxs.book..157M. ISBN:978-0-521-82659-4. section 4.1.5.
  139. ^ "What powers a black hole's mighty jets?". Science | AAAS. 19 نوفمبر 2014. مؤرشف من الأصل في 2019-05-05. اطلع عليه بتاريخ 2018-03-19.
  140. ^ أ ب Celotti، A.؛ Miller، J. C.؛ Sciama، D. W. (1999). "Astrophysical evidence for the existence of black holes" (PDF). Classical and Quantum Gravity. ج. 16 ع. 12A: A3–A21. arXiv:astro-ph/9912186. DOI:10.1088/0264-9381/16/12A/301. مؤرشف من الأصل (PDF) في 2018-07-27.
  141. ^ Winter، L. M.؛ Mushotzky، R. F.؛ Reynolds، C. S. (2006). "XMM‐Newton Archival Study of the Ultraluminous X‐Ray Population in Nearby Galaxies". The Astrophysical Journal. ج. 649 ع. 2: 730–752. arXiv:astro-ph/0512480. Bibcode:2006ApJ...649..730W. DOI:10.1086/506579.
  142. ^ المرصد الأوروبي الجنوبي. "Hubble directly observes the disc around a black hole". www.spacetelescope.org -GB. مؤرشف من الأصل في 2016-03-08. اطلع عليه بتاريخ 2016-03-07.
  143. ^ Muñoz، José A.؛ Mediavilla، Evencio؛ Kochanek، Christopher S.؛ Falco، Emilio؛ Mosquera، Ana María (1 ديسمبر 2011). "A Study of Gravitational Lens Chromaticity with the Hubble Space Telescope". The Astrophysical Journal. ج. 742 ع. 2: 67. arXiv:1107.5932. Bibcode:2011ApJ...742...67M. DOI:10.1088/0004-637X/742/2/67.
  144. ^ Michell, J. (1784). "On the Means of Discovering the Distance, Magnitude, &c. of the Fixed Stars, in Consequence of the Diminution of the Velocity of Their Light, in Case Such a Diminution Should be Found to Take Place in any of Them, and Such Other Data Should be Procured from Observations, as Would be Farther Necessary for That Purpose". Phil. Trans. R. Soc. (London). Philosophical Transactions of the Royal Society of London, Vol. 74. ج. 74: 35–57. مؤرشف من الأصل في 2020-03-20.
  145. ^ "Dark Stars (1783)". Thinkquest. 1999. مؤرشف من الأصل في 2012-10-17. اطلع عليه بتاريخ 2008-05-28.
  146. ^ Laplace; see Israel, Werner (1987), "Dark stars: the evolution of an idea", in Hawking, Stephen W. & Israel, Werner, 300 Years of Gravitation, Cambridge University Press, Sec. 7.4
  147. ^ Thorne (1994:123–124).
  148. ^ Schwarzschild، Karl (1916). "Über das Gravitationsfeld eines Massenpunktes nach der Einsteinschen Theorie". Sitzungsber. Preuss. Akad. D. Wiss.: 189–196. and Schwarzschild، Karl (1916). "Über das Gravitationsfeld eines Kugel aus inkompressibler Flüssigkeit nach der Einsteinschen Theorie". Sitzungsber. Preuss. Akad. D. Wiss.: 424–434.
  149. ^ "Timeline of black holes through history, Newton to the present - Black Holes Encyclopedia" [en]. مؤرشف من الأصل في 2016-10-22. اطلع عليه بتاريخ 2019-12-31.
  150. ^ Oppenheimer, J. R. and Volkoff, G. M. (3 يناير 1939). "On Massive Neutron Cores". Physical Review. ج. 55 ع. 4: 374–381. DOI:10.1103/PhysRev.55.374. مؤرشف من الأصل في 2011-11-20.{{استشهاد بدورية محكمة}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
  151. ^ Ruffini, Remo and Wheeler, John A. (يناير 1971). "Introducing the black hole" (PDF). Physics Today: 30–41. مؤرشف من الأصل (PDF) في 2018-12-11.{{استشهاد بدورية محكمة}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
  152. ^ "Ein Monster im Visier. Astronomen vermessen das Schwarze Loch im Milchstraßenzentrum". wissenschaft.de. 10. Dezember 2008. اطلع عليه بتاريخ 1. Oktober 2009. {{استشهاد ويب}}: تحقق من التاريخ في: |access-date= و|date= (مساعدة)
  153. ^ قالب:مصدر الإنترنت
  154. ^ ناتارجان و تريستر : "هل هناك حد أعلى لكتل الثقوب السوداء؟" 2008. بيب كود: 2009MNRAS.393..838N 2009MNRAS.393..838N.
  155. ^ د. Mortlock وآخرون: كوازار مضيء عند انزياح أحمر لـ z = 7085. Nature، Volume 474، 2011، pp.616-619.
  156. ^ Eduardo Bañados؛ وآخرون (6 ديسمبر 2017). [https: //www.nature.com/articles/nature25180 "ثقب أسود كتلته 800 مليون شمسي في كون محايد بدرجة كبيرة عند انزياح أحمر يبلغ 7.5"]. طبيعة. arXiv:1712.01860. Bibcode:2018Natur.553..473B. DOI:10.1038 / nature25180. اطلع عليه بتاريخ 2018-08-18. {{استشهاد بدورية محكمة}}: Explicit use of et al. in: |مؤلف= (مساعدة)، تأكد من صحة قيمة |doi= (مساعدة)، وتحقق من قيمة |مسار= (مساعدة)
  157. ^ John Regan و John H. Wise و Greg Bryan وآخرون: "التكوين السريع للثقوب السوداء الضخمة على مقربة من المجرات الأولية الجنينية." في: "علم الفلك الطبيعي." مارس 2017 ، [https: //arxiv.org/abs/1703.03805 Arxiv.]
  158. ^ قالب:مصدر الإنترنت
  159. ^ قد تكون الثقوب السوداء الضخمة الهائلة مختبئة في الكون ، في: أخبار 22 يناير 2021 نسخة محفوظة 2021-03-22 على موقع واي باك مشين.
  160. ^ قالب:Internet source
  161. ^ قالب:مصدر الإنترنت
  162. ^ Harald Zaun: '[https: / /www.welt. de / wissenschaft / weltraum / article132372201 / Im-Zentrum-einer-Zwerggalaxie-pulsiert-ein-Monster.html ينبض فائق الكتلة في مركز مجرة قزمة.] "In:" Welt.de . 18 سبتمبر 2014.
  163. ^ أنيل سيث ، ماتياس فرانك ، نادين نيوماير وآخرون: قالب:أرشيف الويب. In: 'Nature.' Vol. 513، 2014، pp. 398-400، Abstract. نسخة محفوظة 2022-12-22 على موقع واي باك مشين.
  164. ^ Rainer Kayser: 380 مليون سنة ضوئية بعيدًا. لاحظ وجود ثقب أسود مزدوج. 20 سبتمبر 2017. نسخة محفوظة 2015-09-01 على موقع واي باك مشين.
  165. ^ Michelle Starr: We Finally Have Evidence That Black Holes Drive Winds Shaping Their Entire Galaxy. In: ScienceAlert.com. 28. Dezember 2017. نسخة محفوظة 2021-12-26 على موقع واي باك مشين.
  166. ^ A. Vayner, Shelley Wright u. a.: Galactic-scale Feedback Observed in the 3C 298 Quasar Host Galaxy. In: Astroph. J. Band 851, 2017, Nr. 2, Abstract. نسخة محفوظة 5 يوليو 2022 على موقع واي باك مشين.
  167. ^ Astronomers Shed Light on Formation of Black Holes and Galaxies. In: KeckObservatory.org. 20. Dezember 2017. نسخة محفوظة 2018-06-13 على موقع واي باك مشين.
  168. ^ النجوم: الاندماج النووي في النجوم - تجميع النواة. من وكالة الفضاء ناسا. تاريخ الولوج 29-12-2010.[وصلة مكسورة] نسخة محفوظة 06 يوليو 2013 على موقع واي باك مشين.
  169. ^ معلومات المستعرات العظيمة: النجوم المتفجرة. من ناشيونال جيوغرافيك. تاريخ الولوج 29-12-2010. نسخة محفوظة 25 ديسمبر 2016 على موقع واي باك مشين.
  170. ^ الاندماج النووي في النجوم. تاريخ الولوج 29-12-2010. نسخة محفوظة 08 2يناير7 على موقع واي باك مشين.
  171. ^ حد تشاندراسيكار. "the internet Encyclopedia of science" (موسوعة العلم الإلكترونية). تاريخ الولوج 29-12-2010. نسخة محفوظة 03 أكتوبر 2017 على موقع واي باك مشين.[وصلة مكسورة]
  172. ^ كيف تتكون الثقوب السوداء؟ نسخة محفوظة 3 أكتوبر 2017 على موقع واي باك مشين.. اسأل فيزيائياً فلكياً - وكالة الفضاء ناسا. تاريخ الولوج 29-12-2010. "نسخة مؤرشفة". مؤرشف من الأصل في 2017-10-03. اطلع عليه بتاريخ 2010-12-29.{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)[وصلة مكسورة]
  173. ^ ولادة الثقب الأسود. تاريخ الولوج 29-12-2010. نسخة محفوظة 12 ديسمبر 2013 على موقع واي باك مشين.
  174. ^ Finkelstein، David (1958). "Past-Future Asymmetry of the Gravitational Field of a Point Particle". Phys. Rev. ج. 110: 965–967. DOI:10.1103/PhysRev.110.965.
  175. ^ Kruskal، M. (1960). "Maximal Extension of Schwarzschild Metric". Physical Review. ج. 119: 1743. DOI:10.1103/PhysRev.119.1743.
  176. ^ Hewish، Antony؛ Bell، S. J.؛ Pilkington، J. D. H.؛ Scott، P. F.؛ Collins، R. A. (1968). "Observation of a Rapidly Pulsating Radio Source". Nature. ج. 217: 709–713. DOI:10.1038/217709a0. مؤرشف من الأصل في 2017-02-26. اطلع عليه بتاريخ 2007-07-06.
  177. ^ Pilkington، J D H؛ Hewish، A.؛ Bell، S. J.؛ Cole، T. W. (1968). "Observations of some further Pulsed Radio Sources" (PDF). Nature. ج. 218: 126–129. DOI:10.1038/218126a0. مؤرشف من الأصل في 2011-05-25. اطلع عليه بتاريخ 2007-07-06.
  178. ^ Newman، E. T.؛ Couch، E.؛ Chinnapared، K.؛ Exton، A.؛ Prakash، A.؛ Torrence، R. (1965). "Metric of a Rotating, Charged Mass". Journal of Mathematical Physics. ج. 6: 918. DOI:10.1063/1.1704351.
  179. ^ Israel، Werner (1967). "Event Horizons in Static Vacuum Space-Times". Physical Review. ج. 164: 1776. DOI:10.1103/PhysRev.164.1776.
  180. ^ Carter، B. (1971). "Axisymmetric Black Hole Has Only Two Degrees of Freedom". Physical Review Letters. ج. 26: 331. DOI:10.1103/PhysRevLett.26.331.
  181. ^ Carter، B. (1977). "The vacuum black hole uniqueness theorem and its conceivable generalisations.". Proceedings of the 1st Marcel Grossmann meeting on general relativity. ص. 243–254.
  182. ^ Robinson، D. (1975). "Uniqueness of the Kerr Black Hole". Physical Review Letters. ج. 34: 905. DOI:10.1103/PhysRevLett.34.905.
  183. ^ Penrose، Roger (1965). "Gravitational Collapse and Space-Time Singularities". Physical Review Letters. ج. 14: 57. DOI:10.1103/PhysRevLett.14.57.
  184. ^ Ford، L. H. (2003). International Journal of Theoretical Physics. ج. 42: 1219. DOI:10.1023/A:1025754515197. {{استشهاد بدورية محكمة}}: الوسيط |title= غير موجود أو فارغ (مساعدة)

مصادر

وصلات خارجية

مجلوبة من «https://3rabica.org/index.php?title=ثقب_أسود&oldid=1262460»