مدخل إلى النسبية العامة

إختبار عالي الدقة للنسبية العامة بواسطة مسبار الفضاء كاسيني (تصور فني) يظهر تأخير إشارات الراديو المرسلة بين الأرض والمسبار (الموجة الخضراء) بانحناء الزمكان (الخطوط الزرقاء) بسبب كتلة الشمس.

النسبية العامة (بالإنجليزية: General relativity)‏، هي نظرية للجاذبية وضعها ألبرت أينشتاين بين عامي 1907 و1915. تنص نظرية النسبية العامة على أن التأثير الملحوظ للجاذبية بين الكتل ناتج عن انحناء الزمكان بفعل هذه الكتل.

حتى أوائل القرن العشرين، ظل قانون الجذب العام لنيوتن مقبولًا لمدة تخطت مئتي عام باعتباره وصفًا صحيحًا لقوة الجاذبية بين الكتل. وفي نموذج نيوتن، تنتج الجاذبية عن قوة جذب بين الأجسام الضخمة. وبالرغم من انزعاج نيوتن نفسه بسبب الطبيعة المجهولة لهذه القوة، ظل الإطار العام لهذه النظرية ناجحًا بشكل كبير في وصف الحركة.

تُبين التجارب والملاحظات أن وصف أينشتاين للجاذبية يفسر العديد من التأثيرات التي لم يتمكن قانون نيوتن من تفسيرها، مثل حالات الشذوذ الطفيف في مدارات عطارد والكواكب الأخرى. تتنبأ النسبية العامة أيضًا بآثار جديدة للجاذبية، مثل الموجات الثقالية، وعدسة الجاذبية، وأثر الجاذبية على الزمن المعروف بتمدد الزمن الثقالي. أُكدت صحة العديد من هذه التنبؤات بالتجربة أو بالرصد، وكان أحدثها الأمواج الثقالية.

تطورت النسبية العامة لتكون أداةً رئيسيةً في علم الفيزياء الفلكية الحديث. فهي توفر الأساس الذي يقوم عليه الفهم الحالي للثقوب السوداء، والمناطق من الفضاء حيث ترتفع فيها قوة الآثار الثقالية لدرجة تحول دون إفلات الضوء. ويُعتقد أن جاذبية هذه المناطق الشديدة مسؤولةً عن الإشعاع الشديد الصادر من بعض الأنواع المعينة من الأجرام الفلكية، مثل الأنوية المجرية أو النجوم الزائفة الدقيقة. تعتبر النسبية العامة أيضًا جزءًا من الإطار القياسي لنموذج الانفجار العظيم بعلم الكونيات.

ورغم أن نظرية النسبية العامة ليست النظرية النسبية الوحيدة للجاذبية، فإنها أبسط نظرية نسبية تتوافق مع البيانات التجريبية. ومع ذلك، يظل هناك عدد من الأسئلة القائمة، أهمها كيفية التوفيق بين النسبية العامة وقوانين فيزياء الكم لإنتاج نظرية كاملة متسقة ذاتيًا للجاذبية الكمية.

من النسبية الخاصة إلى النسبية العامة

في سبتمبر 1905، نشر ألبرت أينشتاين نظريته النسبية الخاصة، والتي توفق بين قوانين نيوتن للحركة والديناميكا الكهربائية (التفاعل بين الأجسام المشحونة كهربيًا). قدمت النسبية الخاصة إطارًا جديدًا للفيزياء باقتراحها لمفاهيم جديدة للزمن والمكان. كان هناك عدم توافق بين هذا الإطار الجديد وبعض النظريات الفيزيائية المقبولة آنذاك؛ وكانت نظرية نيوتن للجاذبية أحد أهم الأمثلة على هذه النظريات، والتي تصف التجاذب المتبادل بين الأجسام بفعل كتلتها.

بحث العديد من الفيزيائيين، مثل أينشتاين، عن نظرية يمكن استخدامها في التوفيق بين قانون الجاذبية لنيوتن والنسبية الخاصة. وكانت نظرية أينشتاين النظرية الوحيدة التي أثبتت أنها متوافقة مع التجارب والملاحظات. ولفهم الأفكار الرئيسية للنظرية، من المفيد اتباع طريقة تفكير أينشتاين بين 1907 و1915، بدءًا من تجربته الفكرية البسيطة التي تدور حول السقوط الحر لمراقب حتى نظريته الهندسية الكاملة للجاذبية.^[1]

مبدأ التكافؤ

يمر الشخص الموجود في مصعد يسقط سقوطًا حرًا بحالة من انعدام الوزن؛ إذ تظل الأجسام داخله طافيةً بلا حركة، أو تنجرف بسرعة ثابتة. ونظرًا لسقوط الأجسام داخل المصعد معًا، لا يمكن ملاحظة أي آثار للجاذبية. وعلى هذا النحو، يصعب تمييز الحالة التي يمر بها المراقب الذي يسقط سقوطًا حرًا عن المراقبين الموجودين في الفضاء العميق، بعيدًا عن أي مصدر كبير للجاذبية. وصف أينشتاين هؤلاء المراقبون المميزون، «القصوريون»، في نظريته النسبية الخاصة: وهم المراقبون الذي يتحرك الضوء بالنسبة لهم في خطوط مستقيمة بسرعة ثابتة.^[2]

افترض أينشتاين أن الحالات المشابهة التي يمر بها المراقبون منعدمو الوزن والقصوريون في النسبية الخاصة مثلت خاصيةً أساسيةً للجاذبية، وجعل هذه الخاصية أساسًا لنظريته النسبية العامة، وصاغها في مبدأ التكافؤ الخاص به. وبشكل عام، ينص المبدأ أن الشخص الموجود في مصعد يسقط سقوطًا حرًا لن يتمكن من تحديد إذا كان في حالة سقوط حر. وأعطت جميع التجارب في هذه الحالة من السقوط الحر نفس نتائج التجارب على المراقبين الساكنين، أو الذين يتحركون حركةً منتظمةً، في الفضاء العميق بعيدًا عن أي من مصادر الجاذبية.^[3]

الجاذبية والتسارع

تتلاشى أغلب آثار الجاذبية في حالة السقوط الحر، ولكن يمكن إصدار آثار مشابهة للجاذبية من خلال إطار مرجعي متسارع. لن يتمكن المراقب الموجود في غرفة مغلقة من تحديد أي مما يلي صحيحًا:

تسقط الأجسام إلى أرضية الغرفة بسبب استقرار الغرفة على سطح الأرض، وبالتالي تنجذب الأجسام إلى الأسفل بفعل الجاذبية الأرضية.
تسقط الأجسام إلى أرضية الغرفة بسبب وجود الغرفة على متن صاروخ في الفضاء بعيدًا عن أي من مصادر الجاذبية، ويتسارع بمعدل 9.8 متر لكل ثانية مربعة، وهي عجلة الجاذبية المعيارية على الأرض. تنجذب الأجسام إلى أرضية الغرفة بفعل نفس «القوة القصورية» التي تدفع سائق السيارة المتسارعة إلى الخلف نحو مقعده.

وبالعكس، يمكن أيضًا ملاحظة أي أثر مرصود في إطار مرجعي متسارع في حقل جاذبية مساوٍ له في القوة. سمح هذا المبدأ لأينشتاين بالتنبؤ بالعديد من الآثار الجديدة للجاذبية عام 1907، كما سنستعرض في القسم التالي.

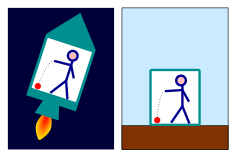
يجب على المراقب الموجود في إطار مرجعي متسارع إدخال ما يسميه عليه الفيزيائيون بالقوى الوهمية لتفسير سبب التسارع الذي يؤثر على المراقب والأجسام من حوله. يعتبر مثال السائق الذي يندفع إلى الخلف نحو مقعده أحد الأمثلة على هذه القوة؛ وتعتبر القوة التي نشعر بها دافعةً أذرعنا إلى الخارج والأعلى، في أثناء الدوران حول أنفسنا مثل لعبة البلبل، أحد الأمثلة الأخرى لهذه القوة. كانت الرؤية الرئيسية لأينشتاين أن الجاذبية المستمرة والمعروفة لحقل جاذبية كوكب الأرض هي في الأساس نفس هذه القوى الوهمية.^[4] ويتناسب المقدار الظاهر لهذه القوى الوهمية دائمًا مع كتلة أي جسم تؤثر عليه، وعلى سبيل المثال، يبذل المقعد قوةً كافيةً لتسريع السائق بنفس معدل تسارع السيارة. وقياسًا على ذلك، رأى أينشتاين أن أي جسم موجود في أي حقل جاذبية يجب أن يتأثر بقوة جاذبية تتناسب مع كتلته، تمامًا كما يصف قانون الجذب العام لنيوتن.^[5]

النتائج الفيزيائية

في عام 1907، كان أينشتاين لا يزال على مسافة 8 سنوات من إكمال نظريته النسبية العامة. ومع ذلك، تمكن من وضع عدد من التنبؤات الجديدة القابلة للاختبار، والتي كانت قائمةً على النقطة التي بدأ منها في تطوير نظريته الجديدة؛ مبدأ التكافؤ.^[6]

كان الانزياح الأحمر الجذبوي للضوء أول الآثار الجديدة. نفترض وجود مراقبين على متن مركبة صاروخية متسارعة. وعلى هذه المركبة، سيكون هناك مفهومًا طبيعيًا «للأعلى» و«الأسفل»؛ إذ سيكون اتجاه تسارع المركبة إلى «الأعلى»، وستتسارع الأجسام غير المثبتة على متن المركبة في الاتجاه المعاكس، لتسقط إلى «الأسفل». ومع افتراض أحد المراقبين في مستوى «أعلى» من الآخر، ومع إرسال المراقب الأدنى إشارة ضوئية إلى المراقب الأعلى، سيُسبب تسارع المركبة انزياحًا أحمر في هذا الضوء، وطبقًا لما يمكن حسابه من النسبية الخاصة؛ سيتمكن المراقب الثاني من حساب تردد أقل لهذا الضوء مقارنةً بتردد الضوء عند المراقب الأول. وبالعكس، سيكون الضوء المرسل من المراقب الأعلى إلى المراقب الأسفل مُزاحًا نحو الطيف الأزرق، أي أنه مُزاح نحو الترددات العالية.^[7] رأى أينشتاين أن هذه الانزياحات في الترددات يجب أن تُرصد أيضًا في أي مجال جاذبية. ويظهر هذا في الشكل الموضح على اليسار، والذي يعرض موجةً ضوئيةً تُزاح إلى الطيف الأحمر تدريجيًا مع حركتها إلى الأعلى ضد تسارع الجاذبية. أُكدت صحة هذا التأثير تجريبيًا.

يتشابه هذا الانزياح الجذبوي في التردد مع تمدد الزمن الثقالي؛ فإذا كان المراقب «الأعلى» يرى نفس الموجة الضوئية بتردد أقل مقارنةً بالمراقب «الأدنى»، يجب على الزمن أيضًا أن يمر بشكل أسرع عند المراقب الأعلى. وبالتالي، فإن الوقت يمر بشكل أبطأ بالنسبة للمراقبين عند الارتفاعات المنخفضة في أي مجال جاذبية.

ومن المهم التأكيد على عدم وجود أي تغيرات مرصودة، بالنسبة لكل مراقب منهما، في سير زمن الأحداث أو العمليات الواقعة في إطارهما الزمني. وبالتالي، ستكون البيضة المسلوقة لمدة 5 دقائق، حسب ساعة كل مراقب، لها نفس القوام في كلتا الحالتين؛ كما أن مرور سنة واحدة حسب ساعة كل مراقب منهما سيؤدي إلى تقدمهما في العمر بنفس المقدار؛ وباختصار، ستكون كل ساعة من الساعتين على توافق تام مع العمليات التي تحدث حولها بشكل مباشر. ويمكن ملاحظة الاختلاف فقط عند مقارنة مرور الوقت على ساعة كل مراقب مع المراقب الآخر؛ إذ سيتضح أن الزمن كان يمر بشكل أبطأ عند المراقب الأدنى بالنسبة للمراقب الأعلى.^[8] ويعتبر هذا التأثير ضئيلًا للغاية، ولكنه أُثبت أيضًا تجريبيًا في العديد من التجارب، كما هو موضح أدناه.

وعلى نفس النحو، تنبأ أينشتاين بالانحراف الثقالي للضوء؛ أي أن الضوء ينحرف نحو الأسفل عند مروره بحقل جاذبية. وبشكل كمي، كانت نتائجه غير دقيقة؛ إذ كان الاستنتاج الصحيح يتطلب صيغةً أكثر تكاملًا باستخدام نظرية النسبية العامة، وليس من مبدأ التكافؤ فحسب.^[9]

التأثيرات المدية

لا يمكن تشكيل نظرية كاملة للجاذبية من التكافؤ بين التأثيرات الثقالية والقصورية. سنتمكن من تقديم تفسير مناسب عند تفسير الجاذبية حول موقعنا من سطح الأرض، مع الإشارة إلى أن إطارنا المرجعي ليس في حالة سقوط حر، إذ يمكن توقع القوى الوهمية. ولكن لا يمكن للإطار المرجعي في حالة السقوط الحر عند أحد جانبي الأرض تقديم تفسير سبب تأثر الناس عند الجانب المقابل من الأرض بقوة جاذبية في الاتجاه المعاكس.

يمكن ملاحظة أحد المظاهر الأساسية الأخرى لنفس التأثير عند سقوط جسمين جنبًا إلى جنب نحو سطح الأرض. ففي إطار السقوط الحر المرجعي لهذين الجسمين، يبدو الجسمان وكأنهما يحومان بلا وزن، ولكن ليس هذا ما يحدث بالضبط. لا يسقط هذان الجسمان في نفس الاتجاه بشكل دقيق، بل يسقطان نحو نقطة مكانية واحدة تُعرف بمركز جاذبية الأرض. وبالتالي، توجد مُركبة لحركة كل جسم في اتجاه الآخر (انظر الشكل). وفي البيئات الصغيرة مثل المصعد الذي يسقط سقوطًا حرًا، سيكون هذا التسارع النسبي ضئيلًا للغاية، ولكن سيكون هذا التأثير كبيرًا بين القافزين بالمظلات عند جانبين متقابلين من الأرض. وتعتبر هذه الفروقات في القوة أيضًا مسؤولةً عن المد والجزر في محيطات الأرض، ولهذا يستخدم مصطلح «التأثير المدي» لوصف هذه الظاهرة.

لا يمكن تفسير التأثيرات المدية عبر التكافؤ بين القصور الذاتي والجاذبية، إذ إنه لن يتمكن من تفسير الاختلافات في مجال الجاذبية.^[10] ولهذا، نحتاج إلى نظرية تصف الطريقة التي تؤثر بها المادة (مثل الكتلة الكبيرة للأرض) على البيئة القصورية من حولها.

من التسارع إلى الهندسة

خلال استكشافه للتكافؤ بين الجاذبية والتسارع بالإضافة إلى دور القوى المدية، اكتشف أينشتاين عدة تشابهات مع هندسة الأسطح. وعلى سبيل المثال، الانتقال من الإطار المرجعي القصوري (الذي تسقط فيه الجسيمات الحرة عبر خطوط مستقيمة بسرعات ثابتة) إلى الإطار المرجعي الدوار (والذي يتطلب إدخال مفاهيم أخرى مناظرة للقوى الوهمية لتفسير حركة الجسيمات فيه)؛ وتتشابه هذه الحالة مع الانتقال من النظام الإحداثي الديكارتي (الذي تكون خطوطه الإحداثية مستقيمةً) إلى نظام الإحداثيات المنحنية (والذي تكون خطوطه الإحداثية غير مستقيمة).

هناك تشابه أعمق يربط بين القوى المدية وإحدى خواص الأسطح المعروفة بالانحناء. بالنسبة لمجالات الجاذبية، وعند اختيار إطار مرجعي في حالة سقوط حر، يمكن لغياب أو وجود القوى المدية تحديد ما إذا كان تأثير الجاذبية يمكن إزالته. وعلى نحو مشابه، يمكن لغياب أو وجود الانحناء تحديد ما إذا كان السطح مكافئًا لسطح مستوٍ. وفي صيف 1912، ألهمت هذه التشابهات أينشتاين حتى بحث عن صيغة هندسية للجاذبية.^[11]

عادةً ما كانت العناصر الأساسية للهندسة؛ النقاط، والخطوط، والمثلثات، تُعرَّف في مكان ثلاثي الأبعاد أو على أسطح ثنائية الأبعاد. وفي عام 1907، قدم هيرمان مينكوفسكي، أستاذ الرياضيات السابق لأينشتاين بالمعهد السويسري الفيدرالي للتكنولوجيا، ما يُعرف بفضاء مينكوفسكي، وهي صيغة هندسية لنظرية النسبية الخاصة لأينشتاين، والتي لم تتضمن المكان فحسب؛ بل تضمنت الزمن أيضًا. كانت الكينونة الأساسية لهذه الهندسة الجديدة زمكانًا رباعي الأبعاد. وبالتالي، فإن مدارات الأجرام المتحركة منحنيات في الزمكان؛ ومدارات الأجرام التي تتحرك بسرعات ثابتة دون تغيير اتجاهها تمثل خطوطًا مستقيمةً.^[12]

طُورت هندسة الأسطح المنحنية العامة في أوائل القرن التاسع عشر بواسطة كارل فريدريش غاوس. وعُممت هذه الهندسة بدورها على الأفضية ذات الأبعاد الأعلى في الهندسة الريمانية التي وضعها برنارد ريمان خلال خمسينيات القرن التاسع عشر. وبمساعدة الهندسة الريمانية، صاغ أينشتاين وصفًا هندسيًا للجاذبية، واستبدل في هذا الوصف زمكان مينكوفسكي بزمكان آخر منحنٍ ومشوه، تمامًا مثل اعتبار الأسطح المنحنية تعميمًا للأسطح المستوية العادية. تستخدم المخططات التضمينية لرسم الزمكان المنحني في السياقات التعليمية.^[13]^[14]

وبعدما أدرك صحة صيغته الهندسية، استغرق أينشتاين ثلاث سنوات أخرى حتى يجد حجر الأساس المفقود لنظريته؛ وهي المعادلات التي تصف كيف تؤثر المادة على انحناء الزمكان. وبعد صياغته لما يُعرف الآن بمعادلات أينشتاين، أو بتعبير أدق؛ معادلات أينشتاين للمجال، قدم أينشتاين نظريته الجديدة للجاذبية في عدة جلسات علمية بالأكاديمية البروسية للعلوم في أواخر 1915، لينتهي منها في عرضه الأخير لنظريته يوم 25 نوفمبر 1915.^[15]

الهندسة والجاذبية

اقتباسًا من جون ويلر، يمكن تلخيص نظرية أينشتاين الهندسية للجاذبية كما يلي: يحكم الزمكان كيفية حركة المادة؛ بينما تحكم المادة كيفية انحناء الزمكان.^[16] سنتناول ما يعنيه هذا التلخيص في الأقسام الثلاثة التالية، التي تستكشف حركة الجسيمات المعروفة بجسيمات الاختبار، وتبحث حول أي من خواص المادة يمكن اعتبارها مصدرًا للجاذبية، وأخيرًا معادلات أينشتاين التي تربط بين هذه الخواص للمادة مع انحناء الزمكان.

فحص مجال الجاذبية

لتخطيط التأثير الثقالي لأحد الأجسام، من المفيد التفكير فيما يُطلق عليه الفيزيائيون جسيمات الاختبار أو الفحص؛ وهي الجسيمات التي تتأثر بالجاذبية ولكنها صغيرة وخفيفة للغاية لدرجة تسمح لنا بإهمال تأثيرها الثقالي الخاص. وفي غياب الجاذبية والقوى الخارجية الأخرى، تتحرك جسيمات الاختبار في خطوط مستقيمة بسرعة ثابتة. وفي لغة الزمكان، يمكن القول بأن هذه الجسيمات تتحرك على طول خطوط العالم المستقيمة في الزمكان. أما في وجود الجاذبية، سيكون الزمكان غير إقليدي، أي منحنيًا، وفي الزمكان المنحني لن تكون خطوط العالم المستقيمة موجودةً. وبدلًا من ذلك، ستتحرك جسيمات الاختبار على طول خطوط تعرف بخطوط الجيوديسي، وهي خطوط «مستقيمة قدر الإمكان»، أي أنها ستتبع أقصر طريق ممكن بين نقطة البداية ونقطة النهاية، مع أخذ الانحناء في الاعتبار.

ويوجد تشابه بسيط: في علم الجيوديسيا، وهو علم قياس مساحة وشكل الأرض، يعتبر الخط الجيوديسي أقصر طريق بين نقطتين على سطح الأرض. وتقريبًا، سيكون هذا الطريق قطاعًا من دائرة كبيرة، مثل خط الطول أو خط الاستواء. وهذه المسارات ليست مستقيمةً بالتأكيد، ببساطة لأنها مجبرة على اتباع انحناء سطح الأرض. ومع ذلك، فهي مستقيمة قدر الإمكان مع خضوعها لهذا الانحناء.

تختلف خواص الخطوط الجيوديسية عن خواص الخطوط المستقيمة. وعلى سبيل المثال، على السطح المستوي، لن تلتقي الخطوط المتوازية أبدًا، ولكن لن يكون هذا صحيحًا بالنسبة للخطوط الجيوديسية؛ فعلى سبيل المثال، تتوازى خطوط الطول عند منطقة الاستواء، ولكنها تتقاطع عند القطبين. وبشكل مماثل، تعتبر خطوط العالم لجسيمات الاختبار في حالة السقوط الحر خطوطًا جيوديسيةً بالزمكان، وهي أكثر الخطوط استقامةً في الزمكان. ولكن ما زالت هناك اختلافات كبيرة بين الخطوط الجيوديسية والخطوط المستقيمة حقًا التي يمكن تتبعها في الزمكان الخالي من الجاذبية بالنسبية الخاصة. ففي النسبية الخاصة، تظل خطوط الجيوديسي المتوازية متوازيةً. أما في مجال الجاذبية مع تأثيراته المدية، لن يكون ذلك صحيحًا بشكل عام. وعلى سبيل المثال، إذا كان هناك جسمان ساكنان في البداية بالنسبة لبعضهما البعض، ثم أُسقطا في مجال جاذبية الأرض، سيتحرك الجسمان باتجاه بعضهما البعض مع سقوطهما نحو مركز الأرض.^[17]

تعتبر الاجسام التي نراها في حياتنا اليومية (الناس، والسيارات، والمنازل، وحتى الجبال) ذات كتلة ضئيلة مقارنةً بالأجرام الفلكية. وعندما يتعلق الأمر بهذه الأجسام، ستكون القوانين التي تحكم سلوك جسيمات الاختبار كافيةً لوصف ما يحدث. وبشكل ملحوظ، يجب التأثير على جسيمات الاختبار بقوة خارجية حتى تنحرف عن مسارها الجيوديسي. يبذل الكرسي الذي يجلس عليه أي شخص قوةً خارجيةً عليه للأعلى، لتمنعه من السقوط الحر نحو مركز جاذبية الأرض، وبالتالي، ستحول هذه القوة دون اتباعه لخط جيوديسي، وهو ما كان سيحدث لولا وجود مادة بين هذا الشخص ومركز جاذبية الأرض. وبهذه الطريقة، تفسر النسبية العامة الجاذبية التي نتأثر بها بشكل يومي على سطح الأرض؛ ليس بأنها قوة جاذبة تسحبنا إلى الأسفل، ولكن بأنها قوى خارجية تدفعنا إلى الأعلى. تدفع هذه القوى جميع الأجسام الساكنة على سطح الأرض عن مساراتها الجيوديسية التي كانت ستتبعها لولا وجود هذه القوى.^[18] أما بالنسبة لمادة الأجرام ذات التأثير الثقالي الكبير الذي لا يمكن إهماله، تعتبر قوانين الحركة أكثر تعقيدًا نوعًا ما مقارنةً بجسيمات الاختبار، ولكن يظل مبدأ أن الزمكان يحكم كيفية حركة المادة صحيحًا.^[19]

مصادر الجاذبية

في وصف نيوتن للجاذبية، تنتج قوى الجاذبية من المادة. وبشكل أكثر دقةً، تنتج هذه القوى من خاصية محددة للأجسام المادية؛ وهي الكتلة. وفي نظرية أينشتاين ونظريات الجاذبية الأخرى المرتبطة بها، ينتج الانحناء الموجود عند كل نقطة في الزمكان من أي مادة موجودة. وهنا أيضًا، تعتبر الكتلة خاصيةً رئيسيةً في تحديد التأثير الثقالي للمادة. وفي النظرية النسبية للجاذبية، لا يمكن للكتلة أن تكون المصدر الوحيد للجاذبية؛ إذ تربط النسبية الكتلة بالطاقة، والطاقة بالزخم.

يعتبر التكافؤ بين الكتلة والطاقة، المُعبر عنه في الصيغة E=mc²، أشهر نتائج النسبية الخاصة. ففي النسبية، تعتبر الكتلة والطاقة طريقتين مختلفتين لوصف كمية فيزيائية واحدة. وإذا كان النظام الفيزيائي يتضمن طاقةً، فسيتضمن أيضًا كتلةً مناظرةً، والعكس صحيح. وتحديدًا، تساهم جميع خواص أي جسم المرتبطة بالطاقة، مثل درجة حرارته أو طاقة ارتباط الأنظمة مثل الأنوية والجزئيات، في كتلة هذا الجسم، وبالتالي يمكن اعتبارها مصدرًا للجاذبية.^[20]

في النسبية الخاصة، ترتبط الطاقة ارتباطًا وثيقًا مع الزخم. وتمامًا مثل اعتبار المكان والزمن، في هذه النظرية، جانبين مختلفين لكيان أكثر شمولًا يُعرف بالزمكان؛ تعتبر الطاقة والزخم مجرد جانبين مختلفين لكمية موحدة رباعية الأبعاد، يطلق عليها الفيزيائيون الزخم الرباعي. ونتيجةً لذلك، فإذا كانت الطاقة مصدرًا للجاذبية، سيكون الزخم مصدرًا لها أيضًا. وسيكون نفس الشيء صحيحًا بالنسبة للكميات التي ترتبط مباشرةً بالطاقة والزخم، والتي تُعرف بالضغط الداخلي والتوتر. وإجمالًا، يمكن اعتبار كلًا من الكتلة، والطاقة، والزخم، والضغط، والتوتر مصادر للجاذبية في النسبية العامة؛ فهي الخواص التي تحكم بها المادة كيفية انحناء الزمكان. وفي الصيغة الرياضياتية للنظرية، تعتبر هذه الكميات مجرد جوانب لكمية فيزيائية أكثر شمولًا تُعرف بموتر الطاقة والزخم.^[21]

معادلات أينشتاين

تعتبر معادلات أينشتاين محورًا للنسبية العامة. فهي تقدم صيغةً دقيقةً للعلاقة بين هندسة الزمكان وخواص المادة، باستخدام لغة الرياضيات. وبشكل ملموس، صيغت هذه المعادلات باستخدام مفاهيم الهندسة الريمانية، والتي تُوصَف فيها الخواص الهندسية للمكان (أو الزمكان) بكمية تسمى المترية. ترمز المترية إلى المعلومات اللازمة لحساب المفاهيم الهندسية الأساسية للمسافة والزوايا في المكان المنحني (أو الزمكان).

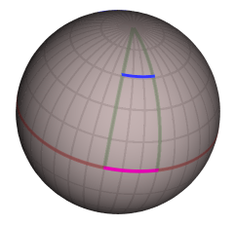
يقدم السطح الكروي، مثل سطح الأرض، مثالًا بسيطًا. يمكن وصف موقع أي نقطة على السطح باستخدام إحداثيين؛ خط العرض الجغرافي، وخط الطول الجغرافي. وبخلاف الإحداثيات الديكارتية للسطح المستوي، لا تتماثل الاختلافات الإحداثية مع المسافات الفعلية على السطح، فكما يظهر في الشكل على اليسار: تبلغ المسافة التي يقطعها شخص ما عند خط الاستواء يتحرك 30 درجةً على خطوط الطول غربًا (الخط الأرجواني) 3300 كيلومتر تقريبًا، بينما تغطي حركة شخص آخر عند خط عرض 55 درجةً، ويتحرك 30 درجةً على خطوط الطول غربًا (الخط الأزرق) مسافة 1900 كيلومتر فقط. وبالتالي، لا تقدم الإحداثيات معلومات كافيةً لوصف هندسة السطح الكروي، أو هندسة أي مكان أو زمكان آخر أكثر تعقيدًا في الواقع. وهذه هي المعلومات التي ترمز إليها المترية بدقة، وهي دالة مُعرفة عند كل نقطة من نقاط السطح (أو المكان، أو الزمكان) وتربط بين الاختلافات الإحداثية والاختلافات في المسافة. يمكن حساب أي من الكميات الهامة الأخرى في الهندسة، مثل طول أي منحنى أو الزاوية الناتجة عن التقاء منحنيين معًا، باستخدام هذه الدالة المترية.^[22]

يمكن استخدام الدالة المترية ومعدل تغيرها بين نقطة وأخرى لتحديد كمية هندسية تسمى موتر انحناء ريمان، والذي يصف بالضبط كيفية انحناء متعدد الشعب الريماني، وهو الزمكان في نظرية النسبية، عند كل نقطة. وطبقًا لما ذُكر بالفعل، يحدد محتوى المادة في الزمكان كميةً أخرى، وهي موتر الطاقة والزخم T، ويعني مبدأ أن «الزمكان يحكم كيفية حركة المادة، والمادة تحكم كيفية انحناء الزمكان» أن هاتين الكميتين يجب أن تكونا على علاقة ببضعهما البعض. صاغ أينشتاين هذه العلاقة باستخدام موتر انحناء ريمان والمترية لتحديد كمية هندسية أخرى G، وهي ما تُعرف الآن بموتر أينشتاين، والذي يصف بعض جوانب طريقة انحناء الزمكان. تنص معادلة أينشتاين على ما يلي:

$G = \frac{8 π G}{c^{4}} T,$

عند مضاعف ثابت، تتناسب الكمية G (التي تقيس الانحناء) مع الكمية T (التي تقيس محتوى المادة). إذ إن G هو ثابت الجذب العام لنيوتن، وc هي سرعة الضوء من النسبية الخاصة.

غالبًا ما يُشار إلى هذه المعادلة بصيغة الجمع، أي معادلات أينشتاين، إذ تُحدَّد كل كمية من الكميتين G وT بواسطة عدة دوال لإحداثيات الزمكان، وتساوي المعادلات كلًا من هذه الدوال المركبة.^[23] يصف حل هذه المعادلات هندسةً معينةً للزمكان؛ فعلى سبيل المثال، يصف حل شوارزشيلد هندسة ما حول الكتلة الكروية غير الدوارة مثل النجوم والثقوب السوداء، بينما يصف حل كير الثقب الأسود الدوار. ولا تزال هناك حلول أخرى يمكن أن تصف الموجات الثقالية، أو الكون المتمدد في حل فريدمان-لوميتر-روبرتسون-ووكر. ويعتبر زمكان مينكوفسكي غير المنحني أبسط الحلول، وهو الزمكان الذي وُصف بواسطة النسبية الخاصة.^[24]

التجارب

مدار نيوتن (بالأحمر)، ومدار أينشتاين (بالأزرق) لكوكب واحد يدور حول نجم كروي.

لا توجد نظرية علمية صحيحة بشكل بديهي؛ إذ تعتبر كل نظرية نموذجًا يجب أن يخضع للفحص عبر التجربة. قُبل قانون نيوتن للجاذبية بسبب تفسيره لحركة الكواكب والأقمار في المجموعة الشمسية بدقة كبيرة. ومع تحسن دقة القياسات التجريبية تدريجيًا، ظهرت بعض التناقضات مع تنبؤات نيوتن، وفُسرت تلك التناقضات في نظرية النسبية العامة. وبشكل مماثل، يجب فحص تنبؤات النسبية العامة بالتجربة أيضًا، وابتكر أينشتاين بنفسه ثلاثة اختبارات تُعرف الآن بالاختبارات الكلاسيكية للنظرية:

تتنبأ الجاذبية النيوتونية بأن المدار الذي يسلكه كوكب واحد حول نجم كروي تمامًا يجب أن يكون إهليجيًا. وتتنبأ نظرية أينشتاين بمنحنى أكثر تعقيدًا؛ إذ يرى أن الكوكب يتصرف وكأنه يدور في مدار إهليجي أيضًا، ولكن في الوقت نفسه، يدور هذا المدار الإهليجي ككل ببطء حول النجم. وفي الشكل على اليسار، يظهر المدار الإهليجي الذي تنبأ به نيوتن باللون الأحمر، بينما يظهر المدار الذي تنبأ به أينشتاين باللون الأزرق. وبالنسبة لكوكب يدور حول الشمس، يُعرف الانحراف عن مدارات نيوتن بانحراف الحضيض الشمسي الشاذ. كان أول قياس لهذا التأثير خاص بكوكب عطارد، ويرجع إلى عام 1859. كانت أكثر القياسات دقةً لهذا التأثير حتى يومنا هذا، لكوكب عطارد والكواكب الأخرى، قائمةً على القياسات التي نُفذت بين 1966 و1990، باستخدام المراصد الراديوية.^[25] تتنبأ النسبية العامة بانحراف الحضيض الشمسي الشاذ بشكل صحيح لجميع الكواكب التي يمكن قياس هذا التأثير عندها بشكل دقيق، وهي عطارد، والزهرة، والأرض.
طبقًا للنسبية العامة، لا يسير الضوء في خطوط مستقيمة عندما ينتشر في مجال جاذبية. وبالتالي، ينحرف الضوء عن مساره في وجود الأجرام الضخمة. وتحديدًا، ينحرف ضوء النجوم عن مساره بسبب مروره بالقرب من الشمس، ما يؤدي إلى انحرافات ظاهرية تصل إلى 1.75 ثانية قوسية في مواقع النجوم بالسماء (تبلغ الثانية القوسية 1/3600 من الدرجة). وفي إطار الجاذبية النيوتونية، يمكن تقديم حجة إرشادية تفيد بانحراف الضوء بنصف هذا المقدار. يمكن اختبار التنبؤين المختلفين من خلال رصد النجوم القريبة من الشمس خلال الكسوف الشمسي. وبهذه الطريقة، أكدت بعثة استكشافية بريطانية إلى أفريقيا الغربية في عام 1919، بقيادة آرثر إدينغتون، صحة تنبؤ أينشتاين وخطأ التنبؤات النيوتونية عبر رصد كسوف مايو 1919 الشمسي. لم تكن نتائج إدينغتون دقيقةً بشكل كبير؛ ولكن أكدت عمليات الرصد التالية لانحراف الضوء الصادر من النجوم الزائفة البعيدة بسبب الشمس، والتي استخدمت تقنيات عالية الدقة لعلم الفلك الراديوي، صحة نتائج إدينغتون بدقة أفضل بشكل كبير، ويرجع أول هذه القياسات إلى عام 1967، ويرجع آخر تحليل شامل لهذا التأثير إلى عام 2004.^[26]
قِيس الانزياح الأحمر الجذبوي لأول مرة بمعدات مختبرية عام 1959 بواسطة باوند وريبيكا. ويمكن رؤية هذه الظاهرة أيضًا في القياسات الفيزيائية الفلكية، خاصةً الضوء الهارب من القزم الأبيض «الشعرى اليمانية ب». وقِيس تأثير تمدد الزمن الثقالي المرتبط بهذه الظاهرة عبر نقل ساعات ذرية إلى ارتفاعات تتراوح بين عشرات وعشرات الآلاف من الكيلومترات (أول مرة كانت في 1971 بواسطة هافيليه وكيتينج؛ وكانت أدق مرة حتى يومنا هذا بواسطة مسبار الجاذبية أ الذي أُطلق عام 1976).^[27]

ومن هذه الاختبارات، عُرف فقط تقدم الحضيض الشمسي لكوكب عطارد قبل نشر أينشتاين لنظرية النسبية بشكل نهائي في 1916. وانطلق أينشتاين إلى النجومية العالمية بعد التأكيد التجريبي التالي لتنبؤاته الأخرى، خاصةً قياسات انحراف الضوء بفعل الشمس عام 1919. وبررت هذه التجارب الثلاث تبني نظرية النسبية العامة بدلًا من نظرية نيوتن، بالإضافة إلى عدد من النظريات المقترحة الأخرى البديلة للنسبية العامة.^[28]

تتضمن الاختبارات الأخرى للنسبية العامة القياسات الدقيقة لتأثير شابيرو أو تأخر الزمن الجذبوي للضوء، والذي قِيس عام 2002 بواسطة مسبار كاسيني الفضائي. تركز مجموعة من الاختبارات على التأثيرات التي تنبأت بها النسبية العامة لسلوك أجهزة الجيروسكوب التي تتحرك في الفضاء. اختُبر التأثير الجيوديسي، وهو من ضمن هذه التأثيرات، بواسطة تجربة المجال الليزري القمري، وهي قياسات عالية الدقة للمدار القمري. وأيضًا، هناك تأثير آخر متعلق بالكتل الدوارة يُعرف بتباطؤ الإطار المرجعي. اختُبر كل من التأثير الجيوديسي وتباطؤ الإطار المرجعي في تجربة بواسطة «مسبار الجاذبية ب»، وهو قمر اصطناعي أُطلق عام 2004، مع نتائج تؤكد النسبية بنحو 0.5% و15% على الترتيب، وذلك حتى ديسمبر 2008.^[29]

وفقًا للمعايير الكونية، تعتبر الجاذبية عبر المجموعة الشمسية ضعيفةً. ولأن الاختلافات بين تنبؤات نظريات أينشتاين ونيوتن تظهر في أوضح صورةً لها عندما تكون الجاذبية قويةً، لطالما اهتم الفيزيائيون باختبار التأثيرات النسبية المختلفة في نظام يتميز بمجالات جاذبية قوية نسبيًا. وأصبح ذلك متاحًا بفضل عمليات الرصد الدقيقة للنوابض الثنائية. ففي مثل هذا النظام النجمي، يدور نجمان نيوترونيان مرتفعا الكثافة بشكل كبير في مدار حول بعضهما البعض. ويكون إحداهما على الأقل نجمًا نابضًا، وهو جرم فلكي يطلق حزمةً قويةً من الموجات الراديوية. تضرب هذه الحزم كوكب الأرض على فترات منتظمة، بشكل مشابه لظهور الشعاع الضوئي الدوار للمنارة كومضات بالنسبة للمراقب، إذ يمكن ملاحظتها في صورة سلسلة منتظمة من النبضات الضوئية. تتنبأ النسبية العامة بوجود بعض الانحرافات المعينة عن هذا التتابع المنتظم في النبضات الراديوية. فعلى سبيل المثال، عند مرور موجة راديوية بالقرب من أحد النجوم النيوترونية، يجب أن تنحرف هذه الموجة عن مسارها بفعل مجال جاذبية هذا النجم. وتتقارب الأنماط المرصودة لهذه النبضات مع الأنماط التي تنبأت بها النسبية العامة بشكل مثير للإعجاب.^[30]

ترتبط مجموعة محددة من الملاحظات بتطبيقات عملية ومفيدة بشكل واضح، تُعرف باسم أنظمة الملاحة عبر الأقمار الاصطناعية، مثل نظام التموضع العالمي (GPS) المستخدم في الملاحة ومتابعة الوقت. تعتمد هذه الأنظمة على مجموعتين من الساعات الذرية؛ مجموعة على متن الأقمار الاصطناعية التي تدور حول الأرض، ومجموعة من الساعات المرجعية الثابتة على سطح الأرض. تتنبأ النسبية العامة أن كل مجموعة من هاتين المجموعتين من الساعات ستتحرك بمعدل مختلف بشكل طفيف عن المجموعة الأخرى؛ بسبب الاختلاف في حركة ساعات كل مجموعة عن الأخرى، وهو تأثير تنبأت به النسبية الخاصة بالفعل، بالإضافة أيضًا إلى اختلاف موقع كل مجموعة عن الأخرى في مجال جاذبية الأرض. ولضمان دقة هذا النظام، يجب إبطاء الساعات الموجودة على الأقمار الاصطناعية بعامل نسبي، أو إدخال هذا العامل النسبي ضمن خوارزمية التقييم. وبالتالي، تعتبر الاختبارات الخاصة بدقة هذا النظام، خاصةً القياسات الشاملة التي ساهمت في تحديد التوقيت العالمي المنسق (UTC)، دليلًا على صحة التنبؤات النسبية.^[31]

فحص عدد من الاختبارات الأخرى صحة نسخ مختلفة من مبدأ التكافؤ؛ فبكل ما تحمله الكلمة من معنى، يمكن اعتبار جميع قياسات تمدد الزمن الثقالي اختبارات لنسخة ضعيفة من هذا المبدأ، وليست للنسبية العامة نفسها. وحتى الآن، اجتازت النسبية العامة كافة الاختبارات الرصدية بنجاح.^[32]

التطبيقات الفيزيائية الفلكية

تلعب النماذج القائمة على النسبية العامة دورًا هامًا في الفيزياء الفلكية؛ كما أن نجاح هذه النماذج دليلًا آخر على صحة النظرية.

عدسة الجاذبية

نظرًا لانحراف الضوء عند مروره عبر مجال الجاذبية، من الممكن للضوء الصادر عن أحد الأجرام البعيدة أن يصل إلى المراقب في صورة مسارين أو أكثر. وعلى سبيل المثال، يمكن أن يمر الضوء الصادر من أحد الأجرام السحيقة مثل النجوم الزائفة عبر أحد جوانب إحدى المجرات الضخمة لينحرف مساره بشكل طفيف حتى يصل إلى مراقب على سطح الأرض، وينحرف أيضًا الضوء المار عبر الجانب الآخر لنفس المجرة؛ وبالتالي، سيصل هذا الضوء الصادر من نفس الجرم إلى نفس المراقب ولكن من اتجاه مختلف بعض الشيء. ونتيجةً لذلك، سيرى هذا المراقب نفس الجرم بمكانين مختلفين في سماء الليل. ويعتبر هذا النوع من التبئير معروفًا في المجالات الخاصة بالعدسات البصرية، وبالتالي، يُعرف التأثير الثقالي المسبب لهذه الظاهرة بعدسة الجاذبية.^[33]

يستخدم علم الفلك الرصدي آثار عدسة الجاذبية باعتبارها أداةً هامةً للاستدلال على خواص الجرم المُسبب لهذه العدسة. وحتى في الحالات التي لا يكون فيها هذا الجرم مرئيًا بشكل مباشر، يمكن لشكل الصورة الظاهرة عبر عدسة الجاذبية الناتجة عنه تقديم معلومات حول توزيع كتلته المسؤولة عن انحراف الضوء. وتحديدًا، تقدم عدسة الجاذبية طريقةً لقياس توزيع المادة المظلمة التي لا يصدر عنها أي ضوء، ما يجعل رصدها معتمد فقط على آثارها الثقالية. وتعتبر عمليات الرصد على المستوى الكبير أحد أهم التطبيقات لهذه الظاهرة بشكل خاص، إذ تنتشر الكتل المسببة لهذه العدسات عبر قطاع كبير من الكون المرصود، وبالتالي يمكن استخدامها للحصول على المعلومات حول تطور كوننا وخواصه على المستوى الكبير.^[34]

الموجات الثقالية

تعتبر الموجات الثقالية أحد النتائج المباشرة لنظرية أينشتاين، وهي تشوهات في هندسة الزمكان تنتشر بسرعة الضوء، ويمكن اعتبارها تموجات في الزمكان. ويجب ألا نخلط بينها وبين موجات الجاذبية في ديناميكا الموائع، والتي تعتبر مفهومًا مختلفًا عنها.

في فبراير 2016، أعلن فريق المرصد المتقدم للموجات الثقالية بالتداخل الليزري (LIGO) عن تمكنه من رصد الموجات الثقالية بشكل مباشر من حدث اندماج ثقبين أسودين.^[35]

وبشكل غير مباشر، رُصد تأثير الموجات الثقالية في عمليات رصد بعض النجوم الثنائية المعينة. تتكون هذه الثنائيات من نجمين يدوران حول بعضهما البعض، ومع دورانهما، يفقدا طاقتهما تدريجيًا عبر إطلاق الموجات الثقالية. وبالنسبة للنجوم العادية مثل الشمس، ستكون الطاقة المفقودة ضئيلةً للغاية لنتمكن من رصدها، ولكن رُصد ذلك الفقد في الطاقة عام 1974 في نابض ثنائي يُسمى PSR1913+16. وفي هذا النظام الثنائي، يكون أحد النجمين نجمًا نابضًا. وسيترتب على هذا النظام نتيجتان: يعتبر النجم النابض جرمًا ذا كثافة عالية للغاية يُعرف باسم النجم النيوتروني، وتكون الموجات الثقالية الناتجة عنه أكبر بكثير من النجوم العادية. وأيضًا، يصدر النابض حزمةً ضيقةً من الإشعاع الكهرومغناطيسي من قطبيه المغناطيسيين. ومع دوران النابض، تمشط حزمته الإشعاعية كوكب الأرض، إذ يُرصد على هيئة سلسلة منتظمة من النبضات الراديوية، بنفس الطريقة التي ترى بيها السفينة الومضات المنتظمة للضوء الصادر من الشعاع الدوار للمنارة. يمكن اعتبار هذا النمط المنتظم من النبضات الراديوية «ساعةً» عالية الدقة. إذ يمكن استخدامه لحساب وقت الفترة المدارية للثنائي النجمي، ويتفاعل هذا النمط بحساسية كبيرة مع تشوهات الزمكان الموجودة حوله مباشرةً.

حصل مكتشفا الثنائي PSR1913+16، وهما راسل هالس وجوزيف تيلور، على جائزة نوبل في الفيزياء عام 1993. ومنذ هذه اللحظة، رُصدت العديد من الثنائيات النابضة. وكان أهم هذه الثنائيات ما كان كلا نجميه نابضًا؛ فهذه الثنائيات تقدم اختبارات دقيقةً للنسبية العامة.^[36]

حاليًا، يوجد عدد من المراصد الأرضية العاملة للموجات الثقالية، كما توجد مهمة أخرى قيد التطوير لإطلاق مرصد فضائي لهذه الموجات، وهو هوائي مقياس التداخل الليزري الفضائي (LISA). ستعمل هذه المهمة مع مهمة «ليزا باثفايندر» السابقة لها، والتي أُطلقت عام 2015. يمكن استخدام عمليات رصد الموجات الثقالية للحصول على المعلومات حول الأجرام عالية الكثافة مثل النجوم النيوترونية والثقوب السوداء، بالإضافة أيضًا إلى فحص حالة الكون المبكر عند أجزاء من الثانية بعد الانفجار العظيم.^[37]

الثقوب السوداء

عندما تتركز المادة إلى منطقة من الفضاء عالية الكثافة بما يكفي، تتنبأ النسبية العامة بتكون ثقبًا أسود، وهي منطقة من الفضاء تتميز بتأثير ثقالي قوي للغاية لدرجة تمنع الضوء نفسه من الإفلات. يُعتقد أن بعض الأنواع المعينة من الثقوب السوداء تمثل الحالة النهائية في تطور النجوم الضخمة. ومن ناحية أخرى، يُفترض أن الثقوب السوداء الفائقة، التي تبلغ كتلتها ملايين أو مليارات الكتل الشمسية، توجد في أنوية أغلب المجرات، وأنها تلعب دورًا هامًا في النماذج الحالية لكيفية تشكل المجرات على مدار مليارات السنين الماضية.^[38]

يعتبر سقوط المادة في الأجسام عالية الكثافة أحد أكفأ الآليات لإطلاق الطاقة في صورة إشعاع، ويُعتقد أن سقوط المادة في الثقوب السوداء مسؤول عن بعض أسطع الظواهر الفلكية التي يمكن تصورها. تعتبر النجوم الزائفة والأنوية المجرية النشطة من بين أبرز الأمثلة التي يهتم بها علماء الفلك بشكل كبير. وفي ظل الظروف الصحيحة، يمكن لسقوط المادة وتراكمها حول الثقوب السوداء أن يؤدي إلى تشكل تدفقات مادية، والتي تقذف حزمًا مركزةً من المادة بعيدًا إلى الفضاء بسرعات تقترب من سرعة الضوء.^[39]

يوجد العديد من الخواص التي تجعل الثقوب السوداء أفضل المصادر الواعدة للموجات الثقالية. وأحد أهم هذه الأسباب كون الثقوب السوداء أعلى الأجرام الفلكية كثافةً، والتي يمكن أن تدور حول بعضها البعض كجزء من نظام ثنائي؛ ونتيجةً لهذه الظاهرة، تعتبر الموجات الثقالية الصادرة عن هذه الأنظمة قويةً بشكل خاص. ويوجد سبب آخر نابع مما يُعرف بنظريات تفرد الثقب الأسود: فمع الوقت، تحتفظ الثقوب السوداء بمجموعة ضئيلة فقط من السمات المميزة لها بصرف النظر عن شكلها الهندسي المبدئي، وأصبحت هذه النظريات معروفةً باسم نظريات «انعدام الشعر». وعلى سبيل المثال، لن يؤدي انهيار مكعب افتراضي من المادة، على المدى الطويل، إلى تكون ثقبًا أسود مكعب الشكل. وبالتالي، لن نتمكن من تمييز هذا الثقب الأسود عن الثقب الذي تكون بفعل انهيار كتلة كروية. وخلال انتقاله إلى الشكل الكروي، سيُصدر الثقب الأسود، الناتج عن انهيار كتلة ذات شكل أكثر تعقيدًا، موجات ثقاليةً.^[40]

الكونيات

تعتبر قابلية تطبيق النسبية العامة على الكون بشكل كلي أحد أهم جوانب هذه النظرية. فمن أهم النقاط الرئيسية أن كوننا يبدو وأنه نشأ على خطوط في غاية البساطة، وذلك على المستويات الكبيرة؛ إذ تقترح كافة عمليات الرصد، في المتوسط، أن بنية الكون يجب أن تكون متماثلةً تقريبًا بصرف النظر عن موقع المراقب أو اتجاه الرصد؛ فالكون نظام متجانس تقريبًا وموحد الخواص. يمكن وصف هذه الأكوان البسيطة نسبيًا عبر الحلول البسيطة لمعادلات أينشتاين. وُضعت النماذج الكونية الحالية للكون عبر دمج هذه الحلول البسيطة للنسبية العامة مع النظريات التي تصف خواص المحتوى المادي للكون، والتي تُعرف بالديناميكا الحرارية، والفيزياء النووية، وفيزياء الجسيمات. وطبقًا لهذه النماذج، نشأ كوننا الحالي من حالة مرتفعة الكثافة والحرارة بشكل كبير، الانفجار العظيم، قبل 14 مليار سنة تقريبًا، وظل الكون يتمدد منذ ذلك الحين.^[41]

يمكن تعميم معادلات أينشتاين من خلال إضافة مصطلح آخر يُعرف باسم الثابت الكوني. وعند وجود هذا المصطلح، يمكن أن نعتبر الفضاء الفارغ نفسه مصدرًا للثقالة التجاذبية (أو أقل شيوعًا، التنافرية). وضع أينشتاين هذا المصطلح أول مرة في ورقته العلمية الرائدة حول الكونيات عام 1917، بدافع محدد للغاية؛ إذ كان الاعتقاد الكوني المعاصر يجعل الكون ثابتًا، وبالتالي كان هذا المصطلح الإضافي ضروريًا لوضع نماذج لأكوان ثابتة في إطار نظرية النسبية العامة. وعندما اتضح أن الكون ليس ثابتًا، ولكنه كون متمدد؛ تخلى أينشتاين سريعًا عن هذا المصطلح الإضافي. ومع ذلك، فمنذ نهاية تسعينيات القرن العشرين، أشارت الأدلة الفلكية إلى تمدد كوني متسارع يتزايد بانتظام، ومتسق مع ثابت كوني أو متسق، بشكل مكافئ، مع نوع محدد وموجود في كل مكان من الطاقة المظلمة.^[42]

الأبحاث العلمية الحديثة

نجحت النسبية العامة بشكل كبير في تقديم إطار للنماذج الدقيقة التي تصف مجموعةً رائعةً من الظواهر الفيزيائية. ومن ناحية أخرى، يوجد العديد من الأسئلة غير المحلولة والمثيرة للاهتمام، وخاصةً أن النظرية ككل تكاد تكون غير مكتملة بشكل مؤكد.^[43]

على عكس جميع النظريات الأخرى الحديثة للقوى الأساسية؛ فإن النسبية العامة نظرية كلاسيكية: فهي لا تتضمن تأثيرات فيزياء الكم. يخاطب البحث عن نسخة كمية لنظرية النسبية العامة أحد أهم الأسئلة الأساسية غير المحلولة في الفيزياء. ورغم وجود عدد من النظريات المرشحة الواعدة لنظرية خاصة بالجاذبية الكمية، أبرزها نظرية الأوتار ونظرية الجاذبية الكمية الحلقية، لا توجد أي نظرية منها متسقة وكاملة حتى الآن. ولطالما كان يأمل العلماء بوجود نظرية للجاذبية الكمية تقضي أيضًا على سمة إشكالية أخرى بالنسبية العامة؛ وهي وجود التفردات الزمكانية. تعتبر هذه التفردات حدودًا، «حواف حادةً»، للزمكان حيث تصبح الهندسة عندها غير واضحة، ما يجعل النسبية العامة نفسها فاقدةً لقدراتها التنبؤية. وعلاوةً على ذلك، هناك ما يُعرف بنظريات التفرد التي تتنبأ بحتمية تواجد مثل هذه التفردات داخل الكون في حالة بقاء قوانين النسبية العامة كما هي دون أي تعديلات كمية. وتعتبر التفردات المرتبطة بالنماذج الكونية التي تصف الثقوب السوداء ونشأة الكون أشهر الأمثلة عليها.^[44]

أُجريت بعض المحاولات الأخرى لتعديل النسبية العامة في سياق الكونيات. ففي النماذج الكونية الحديثة، توجد أغلب طاقة الكون في أشكال لم تُرصد بشكل مباشر على الإطلاق، ما تُعرف بالطاقة المظلمة والمادة المظلمة. كان هناك عدد من الاقتراحات الجدلية بإزالة الحاجة إلى هذه الأشكال المبهمة من المادة والطاقة، من خلال تعديل القوانين التي تحكم الجاذبية وديناميكا تمدد الكون، مثل ديناميكا نيوتن المعدلة.^[45]

بالإضافة إلى تحديات الآثار الكمية والكونيات، يعتبر البحث العلمي في مجال النسبية العامة غنيًا باحتمالات تحقيق المزيد من الاستكشافات: فالنسبيون الرياضياتيون يستكشفون طبيعة التفردات بالإضافة إلى الخواص الأساسية لمعادلات أينشتاين،^[46] كما تُجرى عمليات محاكاة حاسوبية أكثر شمولًا لبعض الزمكانات المعينة (مثل التي تصف اندماج الثقوب السوداء).^[47] وبعد أكثر من مئة عام منذ نشر النظرية للمرة الأولى، أصبح البحث العلمي في هذا المجال أكثر نشاطًا من أي وقت مضى.^[48]

المراجع

^ يمكن الاطلاع على هذا التطور –على سبيل المثال- في رين 2005، ص. 110 من الفصل التاسع إلى الفصل الخامس عشر من بيه 1982 وفي يانسن 2005. يمكن الاطلاع على ملخص جاذبية نيوتن في شوتز 2003، الفصول 2-4. لا يمكن الجزم ما إذا كانت مشكلة جاذبية نيوتن قد خطرت ببال أينشتاين قبل 1907، ولكن بتسليمه الخاص، فإن أولى محاولاته الجادة لإعادة النظر في هذه النظرية من خلال النسبية الخاصة كان في تلك السنة. بيه 1982، ص. 178.
^ نجد هذا بالتفصيل في الفصل الثاني من ويلر 1990.
^ في حين نجد مبدأ التكافؤ لا يزال جزءًا من النسبية العامة الحديثة، إلا أنه هناك بعض الفروقات بين النسخة الحديثة ومفهوم أينشتاين الأصلي. نورتون 1985.
^ يصف أينشتاين نفسه ذلك في الفقرة العشرين في كتابه غير التخصصي أينشتاين 1961. أكمل أينشتاين على أفكار إرنست ماخ السابقة فاستعرض قوى الطرد المركزي ونظيرتها الجذبوية. شتاخل 1989.
^ شرح أينشتاين ذلك في الفقرة العشرين من كتابه أينتشاين 1961، إذ يتأمل جسيمًا "معلقا" بحبل من سقف غرفة على متن صاروخ متسارع: من داخل الغرفة يبدو كما لو كانت الجاذبية تشد الجسيم لأسفل شدًا يتناسب طرديًا مع كتلته، ولكن من خارج الصاروخ يبدو كما لو كان الحبل ينقل تسارع الصاروخ ببساطة إلى الجسيم، وبالتالي لا حاجة لأكثر من بذل القوة لفعل ذلك.
^ لمزيد من الدقة، فقد استُخدمت حسابات أينشتاين، المذكورة في الفصل الحادي عشر ب من بيه 1982 مبدأ التكافؤ –تكافؤ الجاذبية وقوى القصور الذاتي- ونتائج النسبية الخاصة في انتشار الضوء وفي المُراقب المتسارع (الأخيرة عن طريق استعراض أنه وفي كل لحظة فإن الإطار المرجعي القصوري اللحظي مرتبط بهذا المراقب المتسارع.
^ يمكن استخلاص هذا التأثير مباشرةً من النسبية الخاصة، إما عن طريق النظر إلى الوضع المقابل للمشراقبيْن في الصاروخ المتسارع، وإما عن طريق النظر إلى المصعد الساقط. في الحالتين، فإن للانزياح الترددي وصفا مناظرًا مثل تأثير دوبلر بين أُطُر قصورية مختلفة. لاستخلاص بسيط لذلك، راجع هاريسون 2002.
^ راجع الفصل الثاني عشر من ميرمن 2005.
^ إيلرس & رندلر 1997. لمعلومات غير تخصصية راجع بوزل 2007.
^ هذه التأثيرات وغيرها من التأثيرات المدية مذكورة في ويلر 1990، صفحات 83–91.
^ التأثيرات المدية وتفسيراتها الهندسية مذكورة في الفصل الخامس من ويلر 1990. أما هذا الجزء من التطور التاريخي فيمكن الاطلاع عليه في بيه 1982، الفقرة 12 ب.
^ لشروح مبدئية لمفهوم الزمكان، طالع الفقرة الأولى من الفصل الثاني من ثورن 1994، و غرين 2004، ص. 47–61. مزيد من الشروحات في مستوى مبتدئ نجدها في ميرمن 2005 وفي ويلر 1990، الفصلين الثامن والتاسع.
^ مارولف، دونالد (1999). "مخططات تضمين الزمكان للثقوب السوداء". النسبية العامة والجاذبية. ج. 31 ع. 6: 919–944. arXiv:gr-qc/9806123. Bibcode:1999GReGr..31..919M. DOI:10.1023/A:1026646507201. S2CID:12502462.
^ طالع ويلر 1990، الفصلين الثامن والتاسع لمخططات وشروحات مكثفة لانحناء الزمكان.
^ يمكن الاطلاع على جهود أينشتاين لإيجاد معادلات الفيض الصحيحة في الفصول 13-15 من بيه 1982.
^ الفصل التاسع من ويلر 1990.
^ يمكن الاطلاع على شرح شامل لأساسيات الهندسة التفاضلية وتطبيقاتها في النسبية العامة في جيروخ 1978.
^ طالع الفصل العاشر من ويلر 1990.
^ في الحقيقة، فإنه معادلات أينشتاين بإمكانها اشتقاق قوانين الحركة الأكثر تعقيدًا كاستنتاج هندسي، ولكن استنتاج حركة الجسيمات المثالية من ذلك لن يكون مهمة سهلة أبدًا. طالع بواسون 2004.
^ يمكن الاطلاع على تفسير بسيط لتكافؤ الكتلة والطاقة في الفقرات 3.8 و3.9 من جيوليني 2005.
^ طالع الفصل السادس من ويلر 1990.
^ لتعريف أعمق للدالة المترية ولكن أقل تخصصية من المراجع، طالع الفصل 14.4 من بنروز 2004.
^ يمكن الاطلاع على المعني الهندسي لمعادلات أينشتاين في الفصلين السابع والثامن من ويلر 1990 وفي ثورن 1994. كما يمكن الاطلاع على مدخل باستخدام الرياضيات البسيطة في الفصل التاسع عشر من شوتز 2003.
^ يمكن الاطلاع على أهم الحلول في كل مرجع عن النسبية العامة. ولملخص تخصصي لفهمنا الحالي طالع فريدريش 2005.
^ لمزيد من الدقة، فإن قياسات تداخل مديد القاعدة هذه خاصة بالمواقع الكوكبية. طالع الفصل الخامس من ويل 1993 والفقرة 3.5 من ويل 2006.
^ لقياسات تاريخية، طالع هارتل 2005 وكينفيك 2005 وكينفيك 2007; لقد كان استخلاص سولدنر الأصلي في إطار نظرية نيوتن في فون سولدنر 1804. لقياسات حديثة أكثر دقة طالع بيرتوتي 2005.
^ طالع كينفيك 2005 والفصل الثالث من ويل 1993. لقياسات الشعرى اليمانية ب طالع تريمبل & بارستو 2007.
^ بيه 1982, عطارد في ص. 253–254، وذيوع سيط أينشتاين في الفقرات 16ب و16ج.
^ إيفيريت؛ باركنسون (2009)، نتائج مسبار الجاذبية ب _ تقرير ناسا النهائي (PDF)، مؤرشف من الأصل (PDF) في 2021-02-24، اطلع عليه بتاريخ 2009-05-02
^ كرامر 2004.
^ يمكن الاطلاع على وصف للتأثيرات النسبوية في نظام التموضع العالمي في آشبي 2002; مزيد من التفاصيل في آشبي 2003.
^ يمكن الاطلاع على مدخل لتجارب النسبية العامة في ويل 1993; كما يمكن الاطلاع على وصف تخصصي أكثر في ويل 2006.
^ يمكن الاطلاع على الهندسة الخاصة بمثل هذه الظروف في الفصل الثالث والعشرين من شوتز 2003.
^ يمكن الاطلاع على مدخل إلى عدسة الجاذبية وتطبيقاتها في نيوبيري 1997 ولوشنر 2007.
^ ب. آبوت (2016). "رصد موجات الجاذبية الناتجة غن اصطدام ثقبين أسودين". فيزيكال ريفيو ليترز. ج. 116 ع. 6: 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. DOI:10.1103/PhysRevLett.116.061102. PMID:26918975. S2CID:124959784.
^ شوتز 2003، ص. 317–321; بارتوزياك 2000، ص. 70–86.
^ يمكن الاطلاع على البحث الجاري عن موجات الجاذبية في بارتوزياك 2000 و في بلير & مكنمارا 1997.
^ للمحة عن تاريخ فيزياء الثقوب السوداء منذ بدايتها في أول القرن العشرين وحتى الآن، طالع وصف ثورن 1994. ولوصف حديث لدور الثقوب السوداء في تكوين الكتل طالع سبرينغل et al. 2005; طالع ملخصًا أيضا في مقالة غنيدن 2005.
^ طالع الفصل الثامن من سبارك & غالاغر 2007 وديزني 1998. يمكن الاطلاع على وصف أكثر عمقا ولكن برياضيات أساسية فقط في روبسون 1996.
^ يمكن الاطلاع على مدخل ابتدائي لنظريات تفرد الثقوب السوداء في كروشيل 2006 وفي ثورن 1994، ص. 272–286.
^ يمكن الاطلاع على معلومات مفصلة في مدخل ند رايت إلى علم الفلك والأسئلة الشائعة رايت 2007; مدخل سهل القراءة في هوغان 1999. يمكن الاطلاع على وصف أكثر عمقا باستخدام رياضيات غير متقدمة في بيري 1989.
^ مقال أينشتاين الأصلي هو أينشتاين 1917; يمكن الاطلاع على وصف جيد للتطورات حديثة في كووِن 2001 وكالدول 2004.
^ مادوكس 1998، ص. 52–59 و98–122.
^ يمكن الاطلاع على وصف للبحث عن الجاذبية الكمومية مع التركيز على نظرية الأوتار في غرين 1999; لوصف من وجهة نظر الجاذبية الكمومية طالع سمولن 2001.
^ للمادة المظلمة طالع ملغروم 2002; للطاقة المظلمة طالع كالدول 2004
^ طالع فريدريش 2005.
^ نبذة عن مشاكل عديدة والتقنيات اللازمة للتغلب عليها طالع ليهنر 2002.
^ لبداية جيدة للبحث الجاري في النسبية يمكن الاطلاع على صحيفة إلكترونك ريفيو: مقالات حديثة في النسبية. نسخة محفوظة 2016-12-27 على موقع واي باك مشين.

المراجع الأجنبية

Ashby، Neil (2002)، "Relativity and the Global Positioning System" (PDF)، Physics Today، ج. 55، ص. 41–47، Bibcode:2002PhT....55e..41A، DOI:10.1063/1.1485583، PMC:5253894، PMID:28163638، مؤرشف من الأصل (PDF) في 2021-05-07
Ashby، Neil (2003)، "Relativity in the Global Positioning System"، Living Reviews in Relativity، ج. 6، ص. 1، Bibcode:2003LRR.....6....1A، DOI:10.12942/lrr-2003-1، PMC:5253894، PMID:28163638، مؤرشف من الأصل في 2007-07-04، اطلع عليه بتاريخ 2007-07-06
Bartusiak، Marcia (2000)، Einstein's Unfinished Symphony: Listening to the Sounds of Space-Time، Berkley، ISBN:978-0-425-18620-6
Berry، Michael V. (1989)، Principles of Cosmology and Gravitation (ط. 1989 reprinted)، Institute of Physics Publishing، ISBN:0-85274-037-9
Bertotti، Bruno (2005)، "The Cassini Experiment: Investigating the Nature of Gravity"، في Renn، Jürgen (المحرر)، One hundred authors for Einstein، Wiley-VCH، ص. 402–405، ISBN:3-527-40574-7
Blair، David؛ McNamara، Geoff (1997)، Ripples on a Cosmic Sea. The Search for Gravitational Waves، Perseus، ISBN:0-7382-0137-5، مؤرشف من الأصل في 2021-08-17
Caldwell، Robert R. (2004)، "Dark Energy"، Physics World، ج. 17، ص. 37–42، DOI:10.1088/2058-7058/17/5/36، مؤرشف من الأصل في 2018-02-05
Chrusciel، Piotr (2006)، "How many different kinds of black hole are there?"، Einstein Online، مؤرشف من الأصل في 2011-04-14، اطلع عليه بتاريخ 2007-07-15
Cowen، Ron (2001)، "A Dark Force in the Universe"، Science News، Society for Science &#38، ج. 159، ص. 218–220، DOI:10.2307/3981642، JSTOR:3981642
Disney، Michael (1998)، "A New Look at Quasars"، Scientific American، ج. 278، ص. 52–57، Bibcode:1998SciAm.278f..52D، DOI:10.1038/scientificamerican0698-52
Ehlers، Jürgen؛ Rindler، Wolfgang (1997)، "Local and Global Light Bending in Einstein's and other Gravitational Theories"، General Relativity and Gravitation، ج. 29، ص. 519–529، Bibcode:1997GReGr..29..519E، DOI:10.1023/A:1018843001842، hdl:11858/00-001M-0000-0013-5AB5-4، S2CID:118162303
Einstein، Albert (1917)، "Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie"، Sitzungsberichte der Preußischen Akademie der Wissenschaften، ص. 142
Einstein، Albert (1961)، Relativity. The special and general theory، Crown Publishers، مؤرشف من الأصل في 2021-07-20
Friedrich، Helmut (2005)، "Is general relativity 'essentially understood'?"، Annalen der Physik، ج. 15، ص. 84–108، arXiv:gr-qc/0508016، Bibcode:2006AnP...518...84F، DOI:10.1002/andp.200510173، S2CID:37236624
Geroch، Robert (1978)، General relativity from A to B، University of Chicago Press، ISBN:0-226-28864-1
Giulini، Domenico (2005)، Special relativity. A first encounter، Oxford University Press، ISBN:0-19-856746-4
Gnedin، Nickolay Y. (2005)، "Digitizing the Universe"، Nature، ج. 435، ص. 572–573، Bibcode:2005Natur.435..572G، DOI:10.1038/435572a، PMID:15931201، S2CID:3023436
Greene، Brian (1999)، The Elegant Universe: Superstrings, Hidden Dimensions, and the Quest for the Ultimate Theory، Vintage، ISBN:0-375-70811-1، مؤرشف من الأصل في 2022-03-18
Greene، Brian (2004)، The Fabric of the Cosmos: Space, Time, and the Texture of Reality، A. A. Knopf، Bibcode:2004fcst.book.....G، ISBN:0-375-41288-3
Harrison، David M. (2002)، A Non-mathematical Proof of Gravitational Time Dilation (PDF)، مؤرشف من الأصل (PDF) في 2013-03-11، اطلع عليه بتاريخ 2007-05-06
Hartl، Gerhard (2005)، "The Confirmation of the General Theory of Relativity by the British Eclipse Expedition of 1919"، في Renn، Jürgen (المحرر)، One hundred authors for Einstein، Wiley-VCH، ص. 182–187، ISBN:3-527-40574-7
Hogan، Craig J. (1999)، The Little Book of the Big Bang. A Cosmic Primer، Springer، ISBN:0-387-98385-6
Janssen، Michel (2005)، "Of pots and holes: Einstein's bumpy road to general relativity" (PDF)، Annalen der Physik، ج. 14، ص. 58–85، Bibcode:2005AnP...517S..58J، DOI:10.1002/andp.200410130، مؤرشف من الأصل (PDF) في 2017-07-13
Kennefick، Daniel (2005)، "Astronomers Test General Relativity: Light-bending and the Solar Redshift"، في Renn، Jürgen (المحرر)، One hundred authors for Einstein، Wiley-VCH، ص. 178–181، ISBN:3-527-40574-7
Kennefick، Daniel (2007)، "Not Only Because of Theory: Dyson, Eddington and the Competing Myths of the 1919 Eclipse Expedition"، Proceedings of the 7th Conference on the History of General Relativity, Tenerife, 2005، ج. 0709، ص. 685، arXiv:0709.0685، Bibcode:2007arXiv0709.0685K، DOI:10.1016/j.shpsa.2012.07.010، S2CID:119203172
Kramer، Michael (2004)، "Millisecond Pulsars as Tools of Fundamental Physics"، في Karshenboim، S. G.؛ Peik، E. (المحررون)، Astrophysics, Clocks and Fundamental Constants (Lecture Notes in Physics Vol. 648)، Springer، ص. 33–54 (E-Print at astro-ph/0405178)
Lehner، Luis (2002)، "Numerical Relativity: Status and Prospects"، Proceedings of the 16th International Conference on General Relativity and Gravitation, held 15–21 July 2001 in Durban، ص. 210، arXiv:gr-qc/0202055، Bibcode:2002grg..conf..210L، DOI:10.1142/9789812776556_0010، ISBN:978-981-238-171-2، S2CID:9145148
Lochner، Jim، المحرر (2007)، "Gravitational Lensing"، Imagine the Universe Website، NASA GSFC، مؤرشف من الأصل في 2007-06-17، اطلع عليه بتاريخ 2007-06-12
Maddox، John (1998)، What Remains To Be Discovered، Macmillan، ISBN:0-684-82292-X، مؤرشف من الأصل في 2021-08-14
Mermin، N. David (2005)، It's About Time. Understanding Einstein's Relativity، Princeton University Press، ISBN:0-691-12201-6، مؤرشف من الأصل في 2021-08-17
Milgrom، Mordehai (2002)، "Does dark matter really exist?"، Scientific American، ج. 287، ص. 30–37، Bibcode:2002SciAm.287b..42M، DOI:10.1038/scientificamerican0802-42، PMID:12140952، مؤرشف من الأصل في 2011-06-10، اطلع عليه بتاريخ 2007-06-13
Norton، John D. (1985)، "What was Einstein's principle of equivalence?" (PDF)، Studies in History and Philosophy of Science، ج. 16، ص. 203–246، DOI:10.1016/0039-3681(85)90002-0، مؤرشف من الأصل (PDF) في 2021-03-09، اطلع عليه بتاريخ 2007-06-11
Newbury، Pete (1997)، Gravitational lensing webpages، مؤرشف من الأصل في 2012-12-06، اطلع عليه بتاريخ 2007-06-12
Nieto، Michael Martin (2006)، "The quest to understand the Pioneer anomaly" (PDF)، EurophysicsNews، ج. 37، ص. 30–34، arXiv:gr-qc/0702017، Bibcode:2006ENews..37...30N، DOI:10.1051/epn:2006604، S2CID:118949889، مؤرشف من الأصل (PDF) في 2007-06-29
Pais، Abraham (1982)، 'Subtle is the Lord ...' The Science and life of Albert Einstein، Oxford University Press، ISBN:0-19-853907-X، مؤرشف من الأصل في 2022-11-23
Penrose، Roger (2004)، The Road to Reality، A. A. Knopf، ISBN:0-679-45443-8، مؤرشف من الأصل في 2022-07-12
Pössel، M. (2007)، "The equivalence principle and the deflection of light"، Einstein Online، مؤرشف من الأصل في 2007-05-03، اطلع عليه بتاريخ 2007-05-06
Poisson، Eric (2004)، "The Motion of Point Particles in Curved Spacetime"، Living Rev. Relativ.، ج. 7، ص. 6، arXiv:gr-qc/0306052، Bibcode:2004LRR.....7....6P، DOI:10.12942/lrr-2004-6، PMC:5256043، PMID:28179866
Renn، Jürgen، المحرر (2005)، Albert Einstein – Chief Engineer of the Universe: Einstein's Life and Work in Context، Berlin: Wiley-VCH، ISBN:3-527-40571-2
Robson، Ian (1996)، Active galactic nuclei، John Wiley، ISBN:0-471-95853-0
Schutz، Bernard F. (2003)، Gravity from the ground up، Cambridge University Press، ISBN:0-521-45506-5
Smolin، Lee (2001)، Three Roads to Quantum Gravity، Basic، ISBN:0-465-07835-4
von Soldner، Johann Georg (1804)، "Ueber die Ablenkung eines Lichtstrals von seiner geradlinigen Bewegung, durch die Attraktion eines Weltkörpers, an welchem er nahe vorbei geht" ، Berliner Astronomisches Jahrbuch، ص. 161–172.
Sparke، Linda S.؛ Gallagher، John S. (2007)، Galaxies in the universe – An introduction، Cambridge University Press، Bibcode:2007gitu.book.....S، ISBN:978-0-521-85593-8
Springel، Volker؛ White، Simon D. M.؛ Jenkins، Adrian؛ Frenk، Carlos S.؛ Yoshida، N؛ Gao، L؛ Navarro، J؛ Thacker، R؛ Croton، D؛ وآخرون (2005)، "Simulations of the formation, evolution and clustering of galaxies and quasars" (PDF)، Nature، ج. 435، ص. 629–636، arXiv:astro-ph/0504097، Bibcode:2005Natur.435..629S، DOI:10.1038/nature03597، hdl:2027.42/62586، PMID:15931216، S2CID:4383030، مؤرشف من الأصل (PDF) في 2022-11-25
Stachel، John (1989)، "The Rigidly Rotating Disk as the 'Missing Link in the History of General Relativity'"، في Howard، D.؛ Stachel، J. (المحررون)، Einstein and the History of General Relativity (Einstein Studies, Vol. 1)، Birkhäuser، ص. 48–62، ISBN:0-8176-3392-8
Thorne، Kip (1994)، Black Holes and Time Warps: Einstein's Outrageous Legacy، W W Norton & Company، ISBN:0-393-31276-3
Trimble، Virginia؛ Barstow، Martin (2007)، "Gravitational redshift and White Dwarf stars"، Einstein Online، مؤرشف من الأصل في 2011-08-28، اطلع عليه بتاريخ 2007-06-13
Wheeler، John A. (1990)، A Journey Into Gravity and Spacetime، Scientific American Library، San Francisco: W. H. Freeman، ISBN:0-7167-6034-7
Will، Clifford M. (1993)، Was Einstein Right?، Oxford University Press، ISBN:0-19-286170-0
Will، Clifford M. (2006)، "The Confrontation between General Relativity and Experiment"، Living Rev. Relativ.، ج. 9، ص. 3، arXiv:gr-qc/0510072، Bibcode:2006LRR.....9....3W، DOI:10.12942/lrr-2006-3، PMC:5256066، PMID:28179873
Wright، Ned (2007)، Cosmology tutorial and FAQ، University of California at Los Angeles، مؤرشف من الأصل في 2021-07-09، اطلع عليه بتاريخ 2007-06-12

روابط خارجية

يمكن الاطلاع على المزيد من المصادر والمواد المتقدمة هنا.

يتناول هذا الموقع العديد من أفرع الفيزياء النسبية للجمهور أينشتاين أونلاين.
موقع تابع لمجموعة نيومركال ريلاتفتي في المركز الوطني لتطبيقات الحوسبة الفائقة، ويتضمن مقدمة للنسبية العامة والثقوب السوداء وموجات الجذب هنا.

[1] يمكن الاطلاع على هذا التطور –على سبيل المثال- في رين 2005، ص. 110 من الفصل التاسع إلى الفصل الخامس عشر من بيه 1982 وفي يانسن 2005. يمكن الاطلاع على ملخص جاذبية نيوتن في شوتز 2003، الفصول 2-4. لا يمكن الجزم ما إذا كانت مشكلة جاذبية نيوتن قد خطرت ببال أينشتاين قبل 1907، ولكن بتسليمه الخاص، فإن أولى محاولاته الجادة لإعادة النظر في هذه النظرية من خلال النسبية الخاصة كان في تلك السنة. بيه 1982، ص. 178.

[2] نجد هذا بالتفصيل في الفصل الثاني من ويلر 1990.

[3] في حين نجد مبدأ التكافؤ لا يزال جزءًا من النسبية العامة الحديثة، إلا أنه هناك بعض الفروقات بين النسخة الحديثة ومفهوم أينشتاين الأصلي. نورتون 1985.

[4] يصف أينشتاين نفسه ذلك في الفقرة العشرين في كتابه غير التخصصي أينشتاين 1961. أكمل أينشتاين على أفكار إرنست ماخ السابقة فاستعرض قوى الطرد المركزي ونظيرتها الجذبوية. شتاخل 1989.

[5] شرح أينشتاين ذلك في الفقرة العشرين من كتابه أينتشاين 1961، إذ يتأمل جسيمًا "معلقا" بحبل من سقف غرفة على متن صاروخ متسارع: من داخل الغرفة يبدو كما لو كانت الجاذبية تشد الجسيم لأسفل شدًا يتناسب طرديًا مع كتلته، ولكن من خارج الصاروخ يبدو كما لو كان الحبل ينقل تسارع الصاروخ ببساطة إلى الجسيم، وبالتالي لا حاجة لأكثر من بذل القوة لفعل ذلك.

[6] لمزيد من الدقة، فقد استُخدمت حسابات أينشتاين، المذكورة في الفصل الحادي عشر ب من بيه 1982 مبدأ التكافؤ –تكافؤ الجاذبية وقوى القصور الذاتي- ونتائج النسبية الخاصة في انتشار الضوء وفي المُراقب المتسارع (الأخيرة عن طريق استعراض أنه وفي كل لحظة فإن الإطار المرجعي القصوري اللحظي مرتبط بهذا المراقب المتسارع.

[7] يمكن استخلاص هذا التأثير مباشرةً من النسبية الخاصة، إما عن طريق النظر إلى الوضع المقابل للمشراقبيْن في الصاروخ المتسارع، وإما عن طريق النظر إلى المصعد الساقط. في الحالتين، فإن للانزياح الترددي وصفا مناظرًا مثل تأثير دوبلر بين أُطُر قصورية مختلفة. لاستخلاص بسيط لذلك، راجع هاريسون 2002.

[8] راجع الفصل الثاني عشر من ميرمن 2005.

[9] إيلرس & رندلر 1997. لمعلومات غير تخصصية راجع بوزل 2007.

[10] هذه التأثيرات وغيرها من التأثيرات المدية مذكورة في ويلر 1990، صفحات 83–91.

[11] التأثيرات المدية وتفسيراتها الهندسية مذكورة في الفصل الخامس من ويلر 1990. أما هذا الجزء من التطور التاريخي فيمكن الاطلاع عليه في بيه 1982، الفقرة 12 ب.

[12] لشروح مبدئية لمفهوم الزمكان، طالع الفقرة الأولى من الفصل الثاني من ثورن 1994، و غرين 2004، ص. 47–61. مزيد من الشروحات في مستوى مبتدئ نجدها في ميرمن 2005 وفي ويلر 1990، الفصلين الثامن والتاسع.

[13] مارولف، دونالد (1999). "مخططات تضمين الزمكان للثقوب السوداء". النسبية العامة والجاذبية. ج. 31 ع. 6: 919–944. arXiv:gr-qc/9806123. Bibcode:1999GReGr..31..919M. DOI:10.1023/A:1026646507201. S2CID:12502462.

[14] طالع ويلر 1990، الفصلين الثامن والتاسع لمخططات وشروحات مكثفة لانحناء الزمكان.

[15] يمكن الاطلاع على جهود أينشتاين لإيجاد معادلات الفيض الصحيحة في الفصول 13-15 من بيه 1982.

[16] الفصل التاسع من ويلر 1990.

[17] يمكن الاطلاع على شرح شامل لأساسيات الهندسة التفاضلية وتطبيقاتها في النسبية العامة في جيروخ 1978.

[18] طالع الفصل العاشر من ويلر 1990.

[19] في الحقيقة، فإنه معادلات أينشتاين بإمكانها اشتقاق قوانين الحركة الأكثر تعقيدًا كاستنتاج هندسي، ولكن استنتاج حركة الجسيمات المثالية من ذلك لن يكون مهمة سهلة أبدًا. طالع بواسون 2004.

[20] يمكن الاطلاع على تفسير بسيط لتكافؤ الكتلة والطاقة في الفقرات 3.8 و3.9 من جيوليني 2005.

[21] طالع الفصل السادس من ويلر 1990.

[22] لتعريف أعمق للدالة المترية ولكن أقل تخصصية من المراجع، طالع الفصل 14.4 من بنروز 2004.

[23] يمكن الاطلاع على المعني الهندسي لمعادلات أينشتاين في الفصلين السابع والثامن من ويلر 1990 وفي ثورن 1994. كما يمكن الاطلاع على مدخل باستخدام الرياضيات البسيطة في الفصل التاسع عشر من شوتز 2003.

[24] يمكن الاطلاع على أهم الحلول في كل مرجع عن النسبية العامة. ولملخص تخصصي لفهمنا الحالي طالع فريدريش 2005.

[25] لمزيد من الدقة، فإن قياسات تداخل مديد القاعدة هذه خاصة بالمواقع الكوكبية. طالع الفصل الخامس من ويل 1993 والفقرة 3.5 من ويل 2006.

[26] لقياسات تاريخية، طالع هارتل 2005 وكينفيك 2005 وكينفيك 2007; لقد كان استخلاص سولدنر الأصلي في إطار نظرية نيوتن في فون سولدنر 1804. لقياسات حديثة أكثر دقة طالع بيرتوتي 2005.

[27] طالع كينفيك 2005 والفصل الثالث من ويل 1993. لقياسات الشعرى اليمانية ب طالع تريمبل & بارستو 2007.

[28] بيه 1982, عطارد في ص. 253–254، وذيوع سيط أينشتاين في الفقرات 16ب و16ج.

[29] إيفيريت؛ باركنسون (2009)، نتائج مسبار الجاذبية ب _ تقرير ناسا النهائي (PDF)، مؤرشف من الأصل (PDF) في 2021-02-24، اطلع عليه بتاريخ 2009-05-02

[30] كرامر 2004.

[31] يمكن الاطلاع على وصف للتأثيرات النسبوية في نظام التموضع العالمي في آشبي 2002; مزيد من التفاصيل في آشبي 2003.

[32] يمكن الاطلاع على مدخل لتجارب النسبية العامة في ويل 1993; كما يمكن الاطلاع على وصف تخصصي أكثر في ويل 2006.

[33] يمكن الاطلاع على الهندسة الخاصة بمثل هذه الظروف في الفصل الثالث والعشرين من شوتز 2003.

[34] يمكن الاطلاع على مدخل إلى عدسة الجاذبية وتطبيقاتها في نيوبيري 1997 ولوشنر 2007.

[Abbot-35] ب. آبوت (2016). "رصد موجات الجاذبية الناتجة غن اصطدام ثقبين أسودين". فيزيكال ريفيو ليترز. ج. 116 ع. 6: 061102. arXiv:1602.03837. Bibcode:2016PhRvL.116f1102A. DOI:10.1103/PhysRevLett.116.061102. PMID:26918975. S2CID:124959784.

[36] شوتز 2003، ص. 317–321; بارتوزياك 2000، ص. 70–86.

[37] يمكن الاطلاع على البحث الجاري عن موجات الجاذبية في بارتوزياك 2000 و في بلير & مكنمارا 1997.

[38] للمحة عن تاريخ فيزياء الثقوب السوداء منذ بدايتها في أول القرن العشرين وحتى الآن، طالع وصف ثورن 1994. ولوصف حديث لدور الثقوب السوداء في تكوين الكتل طالع سبرينغل et al. 2005; طالع ملخصًا أيضا في مقالة غنيدن 2005.

[39] طالع الفصل الثامن من سبارك & غالاغر 2007 وديزني 1998. يمكن الاطلاع على وصف أكثر عمقا ولكن برياضيات أساسية فقط في روبسون 1996.

[40] يمكن الاطلاع على مدخل ابتدائي لنظريات تفرد الثقوب السوداء في كروشيل 2006 وفي ثورن 1994، ص. 272–286.

[41] يمكن الاطلاع على معلومات مفصلة في مدخل ند رايت إلى علم الفلك والأسئلة الشائعة رايت 2007; مدخل سهل القراءة في هوغان 1999. يمكن الاطلاع على وصف أكثر عمقا باستخدام رياضيات غير متقدمة في بيري 1989.

[42] مقال أينشتاين الأصلي هو أينشتاين 1917; يمكن الاطلاع على وصف جيد للتطورات حديثة في كووِن 2001 وكالدول 2004.

[43] مادوكس 1998، ص. 52–59 و98–122.

[44] يمكن الاطلاع على وصف للبحث عن الجاذبية الكمومية مع التركيز على نظرية الأوتار في غرين 1999; لوصف من وجهة نظر الجاذبية الكمومية طالع سمولن 2001.

[45] للمادة المظلمة طالع ملغروم 2002; للطاقة المظلمة طالع كالدول 2004

[46] طالع فريدريش 2005.

[47] نبذة عن مشاكل عديدة والتقنيات اللازمة للتغلب عليها طالع ليهنر 2002.

[48] لبداية جيدة للبحث الجاري في النسبية يمكن الاطلاع على صحيفة إلكترونك ريفيو: مقالات حديثة في النسبية. نسخة محفوظة 2016-12-27 على موقع واي باك مشين.

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

[22]

[23]

[24]

[25]

[26]

[27]

[28]

[29]

[30]

[31]

[32]

[33]

[34]

[35]

[36]

[37]

[38]

[39]

[40]

[41]

[42]

[43]

[44]

[45]

[46]

[47]

[48]