عمدة عدد مركب
في الرياضيات، عمدة أو سعة العدد المركب (z ≡ x +yi = ||z|| eiθ) (بالإنجليزية: Argument of a complex number) هي عدد حقيقي (بالرمز θ)[1] يوافق الزاوية المحصورة بين المحور الحقيقي وبين الخط الذي يربط بين النقطة الأصل والنقطة صورة العدد المركب. يعرف كذلك بالإزاحة الزاوية.[2]
عمدة عدد مركب |

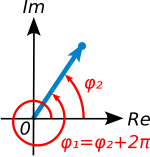
القيمة الرئيسية
نظرًا لأن الدوران الكامل حول الأصل يترك عددًا مركبًا دون تغيير ، فهناك العديد من الخيارات التي يمكن إجراؤها لـعن طريق الدوران حول نقطة الأصل بأي عدة مرات. يظهر هذا في الشكل 2 ، وهو تمثيل للدالة متعددة القيم (مجموعة القيمة) ، حيث يقطع مستقيم عمودي (غير موضح في الشكل) السطح عند ارتفاعات يمثل كل ما هو ممكن.
عندما تكون هناك حاجة إلى دالة معرفة جيدًا، فإن الخيار المعتاد، المعروف باسم القيمة الأساسية، هو القيمة في الفترة المفتوحة - المغلقة (−π rad, π rad]، أي من −π إلى π راديان، باستثناء −π راديان نفسها (ما يعادل من -180 إلى +180 درجة، باستثناء −180 ° نفسها). أي من −π إلى π راديان، باستثناء −π راديان نفسها (تكافئ من -180 إلى +180 درجة، باستثناء −180 درجة نفسها). هذا يمثل زاوية تصل إلى نصف دائرة كاملة من المحور الحقيقي الموجب في أي من الاتجاهين.
يعرِّف بعض المؤلفين مدى القيمة الأساسية على أنه يقع في فترة مفتوحة - مغلقة [0, 2π).
في بعض الأحيان، يُكتب الحرف الأول بأحرف كبيرة للقيمة الأساسية، كما هو الحال في Arg z، خاصة عندما يتم أيضًا النظر في نسخة عامة من العمدة. لاحظ أن التدوين يختلف، لذلك قد يتم تبادل arg و Arg في نصوص مختلفة.
يمكن كتابة مجموعة القيم الممكنة للعمدة بدلالة Arg على شكل:
متطابقات
مثال
الحوسبة انطلاقا من جزئي عدد
إذا كان العدد المركب معرّفًا بدلالة جزئيه الحقيقي والتخيلية، فإن الدالة التي تحسب القيمة الأساسية
Arg تسمى دالة قوس الظل ثنائية العمدة:
- .
دالة قوس الظل ثنائية العمدة متوفرة في مكتبات الرياضيات الخاصة بعديد من لغات البرمجة، وعادة ما تُرجع قيمة في المدى (−π, π].[3]
طالع أيضًا
مراجع
- ^ أو ى
- ^ معنى الإزاحة الزاوية في قاموس المعاني. نسخة محفوظة 17 يناير 2015 على موقع واي باك مشين.
- ^ Weisstein, Eric W. "Complex Argument". mathworld.wolfram.com (بEnglish). Archived from the original on 2022-08-27. Retrieved 2020-08-31.
| عمدة عدد مركب في المشاريع الشقيقة: | |