تكامل متعدد

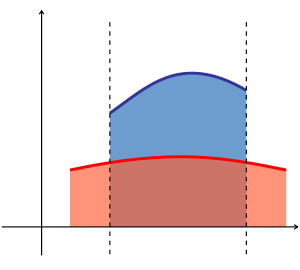
التكامل المتعدد هو أحد أنواع التكامل المحدد الموسع ليشمل الدوال المعرفة في أكثر من متغير مثل $f (x, y)$ أو $f (x, y, z)$ . تسمى تكاملات دالة لمتغيرين على منطقة في R² تكاملات ثنائية،^[1] وتسمى تكاملات دالة ذات ثلاثة متغيرات على منطقة R³ تكاملات ثلاثية.^[1]

مقدمة

كما هو الحال في التكامل المحدد لدالة موجبة في متغير واحد الذي يمثل مساحة المنطقة الواقعة بين منحنى الدالة والمحور السيني، كذلك فإن التكامل الثنائي لدالة موجبة في متغيرين يمثل حجم المنطقة الفاصلة بين السطح المعرف بالدالة (في النظام الديكارتي ثلاثي الأبعاد حيث $f = (x, y)$ والمستوى المحتوي لمجاله. (لاحظ أن نفس الحجم يمكن التوصل إليه باستخدام التكامل الثلاثي - تكامل دالة في ثلاث متغيرات- للدالة الثابتة $f (x, y, z) = 1$ فوق المنطقة المذكورة سابقا بين السطح والمستوى). إذا كان هناك عدد أكبر من المتغيرات فان التكامل المتعدد سيؤدي إلى احجام ضخمة من الدوال المتعددة الأبعاد.

التكامل المتعدد لدالة $f$ المعرفة في $n$ متغير: $f (x_{1}, x_{2}, \dots, x_{n})$ على مجال $D$ يتم في الغالب تمثيله بتداخل عدة إشارات تكامل بالترتيب متعاكس في الحساب (الإشارة إلى أقصى اليسار تحسب آخراً التي تسبقها لليمين تحسب قبلها وهكذا) يتم إجراءها على الدالة وتعريفات المكاملات بترتيب مناسب (التعريف في أقصى اليمين يحسب آخراً وهكذا). مجال هذا التكامل يتم تمثيله إما رمزيا لكل مكامل على إشارة تكامل، أو غالبا يتم اختصاره بمتغير في أقصى يمين الإشارة التكاملية:^[2]

\int \dots \int_{D} f (x_{1}, x_{2}, \dots, x_{n}) d x_{1} \dots d x_{n}

وبما أنه من المستحيل حساب المشتق العكسي لدالة في أكثر من متغير، فإن التكامل المتعدد الغير محدد لا وجود له. لذلك فإن كل التكاملات المتعددة هي تكاملات محددة.

التعريف الرياضي

افترض ان $n$ عدد صحيح أكبر من 1. افترض مستطيلا نصف مفتوح في $n$ بعداً (من الآن فصاعداً سنسميه ببساطة مستطيلا). بالنسبة للمستوى: $n = 2$ , والتكامل المتعدد هو مجرد تكامل ثنائي. $T = (a_{1}, b_{1}) \times (a_{2}, b_{2}) \times \dots \times (a_{n}, b_{n}) \subset ℝ^{n}$

قم بتقسيم كل فترة $(a_{i}; b_{i})$ إلى عدد من الفترات الجزئية غير المتداخلة بحيث تكون كل منها مغلقة عند النهاية اليسرى ومفتوحة عند النهاية اليمنى. بالكتابة، يرمز لكل فترة جزيئة بالرمز $l_{i}$ .عائلة المستطيلات الجرئية الناتجة ذات الصيغة: $C = I_{1} \times I_{2} \times \dots \times I_{n}$

هي جزئية من $T$ بمعنى أن المستطيلات الجزئية $C$ هي مستطيلات غير متداخلة واتحادها يعطينا $T$ . بعد أي من المستطيلات الجزئية $C$ هو-من التعريف- الطول الأكبر من الفترات التي حعلتنا نتحصل على $C$ ، وكذلك فإن بعد أي مجموعة معطاة جزئية من $T$ معرف كأكبر بعد من أبعاد المستطيلات الجزئية في تلك المجموعة الجزئية.

افترض أن $f : T \to R$ هي دالة معرفة على المستطيل $T$ . اعتبر التجزيئ التالي

$T = C_{1} \cup C_{2} \cup \dots \cup C_{m}$

من $T$ المعرفة آنفاً. حيث $m$ هي عدد صحيح موجب. مجموع ريمان هنا هو المجموع بالصورة:

$\sum_{k = 1}^{m} f (P_{k}) m (C_{k})$

حيث، لكل $k$ فان النقطة $P_{k}$ تقع في النفطة $m (C_{k}; C_{k})$ هو ناتج الأطوال من الفترات التي جداءها الديكارتي هو $C_{k}$

في هذه الحالة تسمى دالة $f$ متكاملة ريمان إذا كانت النهاية

$S = \lim_{δ \to 0} \sum_{k = 1}^{m} f (P_{k}) m (C_{k})$

معرفة أو موجودة. حيث ان النهاية تحسب لكل جزئيات $T$ ذات البعد $δ$ .^[3] إذا امكن تكامل $f$ بريمان فان $S$ تسمى تكامل ريمان ل $f$ على $T$ ويكتب:

$\int_{T} f (x) d x .$

تكامل ريمان لدالة معرفة حول مجموعة ذات $n$ بعدا يمكن تعريفها بتوسيع تلك الدالة إلى دالة معرفة على مستطيل نصف مفتوح قيمه تساوي الصفر خارج مجال الدالة الأصلية. إذن فان تكامل الدالة الأصلية على المجال الأصلي هي تكامل الدالة الموسعة على مجالها المستطيل، إذا وُجد.

ما يلي تكامل ريمان في $n$ بعداً سوف يسمى تكاملا متعددا

الخصائص

التكامل المتعدد له العديد من الخصائص المشابة لخصائص تكامل الدوال في متغير واحد (الخطية، التبديلية، الرتابة، الخ). بالإضافة لذلك، وكما في المتغير الواحد، يمكن استخدام التكامل المتعدد لايجاد متوسط الدالة على مجموعة معطاة. أي انه لأي مجموعة معطاة ^{$D \subseteq R^{n}$} ودالة قابلة للتكامل $f$ على $D$ ، القيمة المتوسطة لـ $f$ على مجالها يعطى بـ: $\bar{f} = \frac{1}{m (D)} \int_{D} f (x) d x,$

حيث $m (D)$ هو مقياس $D$

حالات خاصة

في حالة ^{$T \subseteq R^{2}$}، فإن تكامل: $ℓ = \iint_{T} f (x, y) d x d y$

هو تكامل ثنائي ل $f$ على $T$ . وإذا كانت ^{$T \subseteq R^{3}$} فان تكامل:

ℓ = ∭_{T} f (x, y, z) d x d y d z

يكون تكامل ثلاثي ل $f$ على $T$ . لاحظ انه بالتحويل يكون هناك إشارتي تكامل للتكامل الثنائي وثلاث إشارات للتكامل الثلاثي، وهذا يعتبر مجرد تسهيل كتابي يكون عملي عندما نحسب التكامل المتعدد كتكامل متتابع iterated integral (كما سنبين لاحقاً في هذا المقال)

طرق للتكامل

حل المشكلات باستخدام التكامل المتعدد غالباً ما يتم عن طريق إيجاد طريقة لاختزال التكامل المتعدد ليصبح في هيئة سلسلة من التكاملات في متغير واحد تحل كل منها بصورة مباشرة.

فيما يلي بعض طرق التكامل البسيطة:^[4]

الحل المباشر

أحياناً يمكن الحصول على نتيجة التكامل بدون حاجة للتعديل

الدوال الثابتة

في حالة الدالة الثابتة فإن النتيجة مباشرة، ببساطة نقوم بضرب المقياس بالدالة الثابتة $c$ . إذا كانت $c = 1$ وكانت متداخلة مع منطقة جزئية من R² فإن الناتج هو مساحة المنطقة، في حين يكون الناتج هو حجم المنطقة في حالة R³

مثلاً:

D = {(x, y) \in ℝ^{2} : 2 \leq x \leq 4; 3 \leq y \leq 6}

and

f (x, y) = 2

لنكامل $f$ على D بالنسبة ل x أولا:

\int_{3}^{6} \int_{2}^{4} 2 d x d y = area (D) \cdot 2 = (2 \cdot 3) \cdot 2 = 12 .

الحل باستخدام التماثل

إذا وُجد في المجال تماثلٌ حول واحد من المحاور على الأقل، وكانت الدالة لها زوجية parity واحدة على الأقل بالنسبة لمتغير معين. في هذه الحالة تكون قيمة التكامل صفرا (مجموع القيم المتساوية والمتضادة صفر).

من الكافي –في الدوال على Rⁿ – ان يكون المتغير التابع فردي مع محور التماثل.

مثال (1):

خذ f(x, y) = 2 sin x − 3y³ + 5

وT = x² + y² ≤ 1 مساحة التكامل (قرص ذو نصف قطر 1 يتركز عند نقطة أصل المحور شاملاً المحيط).

مستخدما خاصية الخطية يمكن تفكيك التكامل إلى ثلاثة أجزاء:

\iint_{T} (2 \sin x - 3 y^{3} + 5) d x d y = \iint_{T} 2 \sin x d x d y - \iint_{T} 3 y^{3} d x d y + \iint_{T} 5 d x d y

2 sin x' و 3y³ كلاهما دالتين فرديتين ومن الواضح كذلك ان قرص T متماثل حول محور x وكذلك محور y؛ لذلك فان القيمة الوحيدة التي سنحصل عليها في الإجابة النهائية لتكامل الدوال الثلاث هي حل الدالة الثابتة 5 لأن الدالتين الأخرتين تساوي صفرا.

مثال (2):

خد الدالة (f(x, y, z) = x exp(y² + z² ومنطقة التكامل هي كرة ذات نصف قطر 2 متركزة في نقطة أصل المحور T = x² + y² + z² ≤ 4. الكرة متماثلة حول جميع المحاور الثلاثة، لكن يكفي ان نكاملها باعتبار محور x فقط لنجد أن التكامل يساوي صفرا؛ ذلك لأن الدالة فردية بالنسبة لذلك المتغير x.

صيغ الاختزال

صيغ الاختزال تعتمد على مبدأ المجال البسيط للتمكين من تفكيك التكامل المتعدد إلى عدة تكاملات في متغير واحد (وهي نفس عملية حسبان الاشتقاق الجزئي).

المجالات البسيطة على R²

محور x

إذا كان D مجال مقيس عمودي على محور x و $f : D ⟶ ℝ$ هي دالة مستمرة؛ فإن (α(x و (β(x (بالتعريف في الفترة [a, b]) هما دالتين اللتين تحددان D. إذن:

\iint_{T} f (x, y) d x d y = \int_{a}^{b} d x \int_{α (x)}^{β (x)} f (x, y) d y .

محور y

إذا كان D مجال مقيس عمودي على محور y و $f : D ⟶ ℝ$ هي دالة مستمرة؛ فإن (α(y و (β(y (بالتعريف في الفترة [a, b]) هما دالتين اللتين تحددان D. إذن:

\iint_{T} f (x, y) d x d y = \int_{a}^{b} d y \int_{α (y)}^{β (y)} f (x, y) d x .

مثال

اعتبر أن المنطقة $D = {(x, y) : x \geq 0, y \leq 1, y \geq x^{2}}$ (انظر الشكل المقابل). احسب: $\iint_{D} (x + y) d x d y .$

هذا المجال عمودي على كلا المحورين xو y. لتطبيق صيغ الاختزال عليك ان تجد الدوال التي تحدد المجال وفترة تعريفه.

في هذه الحالدة الدالتين هما:

α (x) = x^{2} and β (x) = 1

بينما الفترة معطاة من تقاطع الدوال مع x = 0، عليه فان الفترة هي [a, b] = [0, 1](جعلنا الوضع الأساسي باعتبار محور x لسهولة فهمها من الشكل المقابل). من الممكن الآن تطبيق الصيغة:

\iint_{D} (x + y) d x d y = \int_{0}^{1} d x \int_{x^{2}}^{1} (x + y) d y = \int_{0}^{1} d x {[x y + \frac{y^{2}}{2}]}_{x^{2}}^{1}

(في البداية التكامل الثاني تم حسابه باعتبار ان x ثابت). كل ما يتبقى هو تطبيق عمليات تكاملية بسيطة::

\int_{0}^{1} {[x y + \frac{y^{2}}{2}]}_{x^{2}}^{1} d x = \int_{0}^{1} (x + \frac{1}{2} - x^{3} - \frac{x^{4}}{2}) d x = \dots = \frac{13}{20} .

إذا أردنا جعل الوضع الأساسي باعتبار لمحور yنقوم بالآتي:

\int_{0}^{1} d y \int_{0}^{\sqrt{y}} (x + y) d x .

وسنحصل على نفس النتيجة

المجالات البسيطة على R³

امتداد هذه الصيغ إلى التكاملات الثلاثية مشابه نوعاً ما: T هو مجال عمودي على المستوى xy باعتبار الدوال (α (x,y و (β(x,y، إذن:

∭_{T} f (x, y, z) d x d y d z = \iint_{D} d x d y \int_{α (x, y)}^{β (x, y)} f (x, y, z) d z

تغيير المتغيرات

حدود التكامل غير سهلة التغيير عادة، (بدون normality أو مع صيغ معقدة للمكاملة)، نقوم بـ«تغيير المتغيرات» لنعيد صياغة التكامل في منطقة أسهل في التعامل، والتي يمكن وصفها بصيغ مماثلة. لعمل ذلك يجب جعل الدالة تتماشى مع الإحداثيات الجديدة.

مثال (1-أ)

الدالة هي

f (x, y) = (x - 1)^{2} + \sqrt{y}

;

إذا تبنينا هذا البديل

x^{'} = x - 1, y^{'} = y

لذلك

x = x^{'} + 1, y = y^{'}

نحصل على الدالة الجديدة

f_{2} (x, y) = (x^{'})^{2} + \sqrt{y}

.

وبصورة مشابة للمجال لأنه لم يعد محدودا بالمتغيرات الاصلية التي تم تحويلها (x ,y في المثال).
التفاضلات (d(xو (d(y يتم تحويلها عبر محددة المصفوفة الجاكوبية

المحتوية على الاشتقاقات الجزئية من التحويل والمتعلقة بالمتغير الجديد (على سبيل المثال التحويل التفاضلي في الإحداثيات القطبية).

توجد ثلاثة أنواع من تغيير المتغيرات (واحد في R² واثنان في R³)؛ لكن البديل المناسب يمكن إيجاده باستخدام نفس المبدأ بصورة أكثر عمومية.

الإحداثيات القطبية

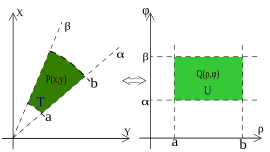
في R² إذا كان المجال له تماثل دائري وتوفرت في الدالة مواصفات «معينة» يمكننا حينها التحويل إلى احداثيات قطبية (انظر للمثال المقابل) مما يعني أن النقاط المبدئية (P(x,y في النظام الديكارتي تتحول إلى النقاط التي تمثلها في النظام القطبي مما يسمح بتغيير صورة المجال وتبسيط العملية.

العلاقة الأساسية لعمل التحويل هي التالية:

f (x, y) \to f (ρ \cos ϕ, ρ \sin ϕ) .

مثال (2-أ):

الدالة هي

f (x, y) = x + y

وبتطبيق التحويل نحصل على:

f (ρ, ϕ) = ρ \cos ϕ + ρ \sin ϕ = ρ (\cos ϕ + \sin ϕ) .

مثال (2-ب):

الدالة هي

f (x, y) = x^{2} + y^{2}

في هذه الحالة لدينا:

f (ρ, ϕ) = ρ^{2} (\cos^{2} ϕ + \sin^{2} ϕ) = ρ^{2}

باستخدام مبرهنة فيثاغورث يتم تحويل المجال بايجاد طول نصف القطر ومدى الزاوية المركزية لتعريف فترات ρو φ ابتداءً من x وy

مثال (2-ج):

المجال هو

D = x^{2} + y^{2} \leq 4

وهو محيط ذو نصف قطر 2؛ من الواضح أن الزاوية المغطاة هي زاوية دائرة، إذن φ تتراوح بين 0 و 2π, بينما يتراوح نصف القطر من 0 إلى 2

مثال (2-د):

المجال هو

D = {x^{2} + y^{2} \leq 9, x^{2} + y^{2} \geq 4, y \geq 0}

وهو القوس الدائري الواقع في الجزء الموجب من محور y (أنظر الشكل)، لاحظ ان φ تصف زاوية مستوى، بينما ρ تتراوح بين 2 و3. لذلك التحويل الناتج يكون المستطيل التالي:

T = {2 \leq ρ \leq 3, 0 \leq ϕ \leq π} .

المحددة الجاكوبية لهذا التحويل هي:

\frac{\partial (x, y)}{\partial (ρ, ϕ)} = | \begin{matrix} \cos ϕ & - ρ \sin ϕ \\ \sin ϕ & ρ \cos ϕ \end{matrix} | = ρ

والتي تم التحصل عليها بادخال المشتقات الجزئية ل (x == ρ cos(φ و (y == ρ sin(φ في العمود الأول باعتبار ρ، وفي العمود الثاني باعتبار φ، لذا فإن التفاضلات dx dy في هذا التحويل تصبح ρ dρ dφ.

ما ان تحول الدالة وتقيم المجال يصبح من الممكن أن تعرف الصيغة لتغيير المتغيرات في الإحداثيات القطبية: $\iint_{D} f (x, y) d x d y = \iint_{T} f (ρ \cos ϕ, ρ \sin ϕ) ρ d ρ d ϕ .$

لاحظ أن φ صالحة في الفترة [0, 2π] بينما ρ والتي تمثل مقياس الطول لابد أن تكون موجبة القيمة.

مثال (2-هـ):

الدالة هي ƒ(x, y) = x والمجال هو نفس مجال المثال (2-د).

من التحليل السابق ل D نعلم فترة ρ (بين 2 و 3) وفترة φ (بين 0 و 2π).إذن لنقم بتغيير الدالة:

f (x, y) = x ⟶ f (ρ, ϕ) = ρ \cos ϕ .

أخيراً، لنطبق صيغ التكامل:

\iint_{D} x d x d y = \iint_{T} ρ \cos ϕ ρ d ρ d ϕ .

بتعريف الفترة يصبح لدينا:

\int_{0}^{π} \int_{2}^{3} ρ^{2} \cos ϕ d ρ d ϕ = \int_{0}^{π} \cos ϕ d ϕ {[\frac{ρ^{3}}{3}]}_{2}^{3} = {[\sin ϕ]}_{0}^{π} (9 - \frac{8}{3}) = 0 .

الإحداثيات الأسطوانية

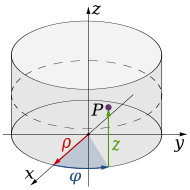
في R³ التكامل على مجالات ذات قواعد دائرية يمكن ان يتم عن طريق التمرير في الإحداثيات الأسطوانية؛ تحويل الدالة يتم من خلال العلاقة التالية:

f (x, y, z) \to f (ρ \cos ϕ, ρ \sin ϕ, z)

يمكن تحويل المجال بيانياً لأن الاختلاف الوحيد يكون في شكل القاعدة، بينما الارتفاع يتبع شكل منطقة البداية.

مثال (3-أ):

المنطقة هي

D = {x^{2} + y^{2} \leq 9, x^{2} + y^{2} \geq 4, 0 \leq z \leq 5}

(وهي الأنبوب الذي قاعدته هي الدائرة في مثال (2-د) والتي ارتفاعها 5)؛ إذا طُبق التحويل نتحصل على المنطقة:

T = {2 \leq ρ \leq 3, 0 \leq ϕ \leq π, 0 \leq z \leq 5}

(وهو متوازي المستطيلات الذي قاعدته المستطيل في مثال (2-د) ذو الارتفاع 5).

ولأن العنصر z لا يتغير خلال التحويل فإن المشتقات dx dy dz تتفاوت كما في التمرير في الإحداثيات القطبية؛ لذلك يصبحون ρ dρ dφ dz.

أخيراً من الممكن تطبيق الصيغة النهائية للإحداثيات الأسطوانية:

∭_{D} f (x, y, z) d x d y d z = ∭_{T} f (ρ \cos ϕ, ρ \sin ϕ, z) ρ d ρ d ϕ d z .

هذه الطريقة سهلة ومناسبة للمجالات الأسطوانية والمخروطية أو في المناطق التي يسهل فيها افراد فترة z، وحتى تحوبل القاعدة الدائرية والدالة.

مثال (3-ب):

الدالة هي

f (x, y, z) = x^{2} + y^{2} + z

، ومجال التكامل هو هذه الأسطوانة:

D = {x^{2} + y^{2} \leq 9, - 5 \leq z \leq 5}

تحويل D في إحداثيات أسطوانية هو الآتي:

T = {0 \leq ρ \leq 3, 0 \leq ϕ \leq 2 π, - 5 \leq z \leq 5} .

بينما تصبح الدالة::

f (ρ \cos ϕ, ρ \sin ϕ, z) = ρ^{2} + z

أخيراً، نطبق صيغة التكامل::

∭_{D} (x^{2} + y^{2} + z) d x d y d z = ∭_{T} (ρ^{2} + z) ρ d ρ d ϕ d z;

بتعديل الصيغة نحصل على::

\int_{- 5}^{5} d z \int_{0}^{2 π} d ϕ \int_{0}^{3} (ρ^{3} + ρ z) d ρ = 2 π \int_{- 5}^{5} {[\frac{ρ^{4}}{4} + \frac{ρ^{2} z}{2}]}_{0}^{3} d z

= 2 π \int_{- 5}^{5} (\frac{81}{4} + \frac{9}{2} z) d z = \dots = 405 π .

الإحداثيات الكروية

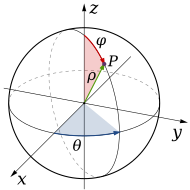
بعض المجالات في R³ لها تماثل دائري، لذلك فمن الممكن تحديد احداثيات كل نقاط منطقة التكامل بزاويتين ومسافة واحدة لذلك نستخدم التمرير في إحداثيات كروية ، ويتم تحويل الدالة بالعلاقة:

f (x, y, z) ⟶ f (ρ \cos θ \sin ϕ, ρ \sin θ \sin ϕ, ρ \cos ϕ)

لاحظ أن النقاط الموجودة على محور x لا تمتلك مواصفات دقيقة في الإحداثيات الكروية، لذلك فقد تتراوح $ϕ$ بين 0 وπ.

من الواضح ان أفضل مجال تكاملي لهذا التمرير هو الكرة.

مثال (4-أ): خذ المجال $D = x^{2} + y^{2} + z^{2} \leq 16$ (دائرة نصف قطرها 4 ومركزها نقطة الأصل)؛ بتطبيق التحويل نحصل على المنطقة: $T = {0 \leq ρ \leq 4, 0 \leq ϕ \leq π, 0 \leq θ \leq 2 π} .$

محددة الجاكوبي لهذا التحويل هي التالية:

\frac{\partial (x, y, z)}{\partial (ρ, θ, ϕ)} = | \begin{matrix} \cos θ \sin ϕ & - ρ \sin θ \sin ϕ & ρ \cos θ \cos ϕ \\ \sin θ \sin ϕ & ρ \cos θ \sin ϕ & ρ \sin θ \cos ϕ \\ \cos ϕ & 0 & - ρ \sin ϕ \end{matrix} | = ρ^{2} \sin ϕ

المشتقات dx dy dz تتحول إلى ρ² sin(φ) dρ dθ dφ.

أخيراً، نتحصل على صيغة التكامل النهائية:

∭_{D} f (x, y, z) d x d y d z = ∭_{T} f (ρ \sin ϕ \cos θ, ρ \sin ϕ \sin θ, ρ \cos ϕ) ρ^{2} \sin ϕ d ρ d θ d ϕ .

يُفضل استعمال هذه الطريقة في حالة المجالات الدائرية و كذلك في حالة الدوال التي يمكن تبسيطها بسهولة -باستخدام العلاقة المثلثية الأساسية الأولى - موسع في R³ (الرجاء انظر مثال (4-ب))؛ يفضل في بعض الحالات الأخرى استخدام الإحداثيات الإسطوانية (انظر مثال 4-جـ).

مثال (4-ب):

D هي نفس المنطقة في مثال (4-أ) و

f (x, y, z) = x^{2} + y^{2} + z^{2}

هي الدالة التي نرغب في مكاملتها.

تحويلها سهل جدا:

f (ρ \sin ϕ \cos θ, ρ \sin ϕ \sin θ, ρ \cos ϕ) = ρ^{2},

بينمانعرف فترة المنطقة T الناتجة عن تحويل D:

(0 \leq ρ \leq 4, 0 \leq ϕ \leq π, 0 \leq θ \leq 2 π) .

نبدأ إذن بتطبيق صيغة التكامل:

∭_{D} (x^{2} + y^{2} + z^{2}) d x d y d z = ∭_{T} ρ^{2} ρ^{2} \sin θ d ρ d θ d ϕ,

وبالتبسيط نحصل على:

∭_{T} ρ^{4} \sin θ d ρ d θ d ϕ = \int_{0}^{π} \sin ϕ d ϕ \int_{0}^{4} ρ^{4} d ρ \int_{0}^{2 π} d θ = 2 π \int_{0}^{π} \sin ϕ {[\frac{ρ^{5}}{5}]}_{0}^{4} d ϕ

= 2 π {[\frac{ρ^{5}}{5}]}_{0}^{4} {[- \cos ϕ]}_{0}^{π} = 4 π \cdot \frac{1024}{5} = \frac{4096 π}{5} .

مثال (4-جـ):

المجال هو الكرة التي مركزها نقطة الأصل ونصف قطرها 3a (

D = x^{2} + y^{2} + z^{2} \leq 9 a^{2}

) و

f (x, y, z) = x^{2} + y^{2}

هي دالة المراد مكاملتها.

بالنظر للمجال يبدو أنه من المناسب القيام بالتمرير إلى إحداثيات كروية، في الحقيقة، من الواضح أن فترات المتغيرات التي تحدد المنطقة الجديدة T هي:

0 \leq ρ \leq 3 a, 0 \leq ϕ \leq 2 π, 0 \leq θ \leq π .

ولكن، بتطبيق التحويل نحصل على:

f (x, y, z) = x^{2} + y^{2} ⟶ ρ^{2} \sin^{2} θ \cos^{2} ϕ + ρ^{2} \sin^{2} θ \sin^{2} ϕ = ρ^{2} \sin^{2} θ

.

بتطبيق صيغة التكامل نحصل على:

∭_{T} ρ^{2} \sin^{2} θ ρ^{2} \sin θ d ρ d θ d ϕ = ∭_{T} ρ^{4} \sin^{3} θ d ρ d θ d ϕ

والذي يصعب حله، هذه المسألة يتم حلها بالتمرير إلى احداثيات أسطوانية، وتصبح فترات T الجديدة هي:

0 \leq ρ \leq 3 a, 0 \leq ϕ \leq 2 π, - \sqrt{9 a^{2} - ρ^{2}} \leq z \leq \sqrt{9 a^{2} - ρ^{2}};

تم التحصل على الفترة z بشق الكرة إلى نصفين ببساطة عن طريق حل المتباينة في صيغة D (وبعدها مباشرة تحويل x² + y² إلى ρ²). الدالة الجديدة تصبح أذن ρ². بتطبيق صيغة التكامل:

∭_{T} ρ^{2} ρ d ρ d ϕ d z

.

نحصل بعدها على:

\int_{0}^{2 π} d ϕ \int_{0}^{3 a} ρ^{3} d ρ \int_{- \sqrt{9 a^{2} - ρ^{2}}}^{\sqrt{9 a^{2} - ρ^{2}}} d z = 2 π \int_{0}^{3 a} 2 ρ^{3} \sqrt{9 a^{2} - ρ^{2}} d ρ .

الآن نطبق التحويل:

9 a^{2} - ρ^{2} = t ⟶ d t = - 2 ρ d ρ ⟶ d ρ = \frac{d t}{- 2 ρ}

(الفترات الجديدة تصبح

0, 3 a ⟶ 9 a^{2}, 0

). نحصل على:

- 2 π \int_{9 a^{2}}^{0} ρ^{2} \sqrt{t} d t

ولأن

ρ^{2} = 9 a^{2} - t

، نحصل على:

- 2 π \int_{9 a^{2}}^{0} (9 a^{2} - t) \sqrt{t} d t,

بعد قلب حدود التكامل وضرب الأطراف داخل القوسين، يمكن تفكيك التكامل إلى جزئين يُحلان مباشرة.

2 π [\int 0^{9 a^{2}} 9 a^{2} \sqrt{t} d t - \int 0^{9 a^{2}} t \sqrt{t} d t] = 2 π {[9 a^{2} \frac{2}{3} t^{\frac{3}{2}} - \frac{2}{5} t^{\frac{5}{2}}]}_{0}^{9 a^{2}}

= 2 \cdot 27 π a^{5} (6 - \frac{2}{5}) = 54 π \frac{28}{5} a^{5} = \frac{1512 π}{5} a^{5} .

الفضل في إمكانية اختزال التكامل الثلاثي لآخر أسهل في متغير واحد يعود لطريقة التمرير إلى إحداثيات أسطوانية

أمثلة

التكامل الثنائي

لنفترض أننا نرغب في مكاملة دالة في عدة متغيرات f خلال منطقة A :

A = {(x, y) \in ℝ^{2} : 11 \leq x \leq 14; 7 \leq y \leq 10}

و

f (x, y) = x^{2} + 4 y

لهذه الحالة نكون التكامل الثنائي:: $\int_{7}^{10} \int_{11}^{14} (x^{2} + 4 y) d x d y$

يتوجه النظر إلى التكامل الداخلي أولاً والذي نكامله باعتبار x، يجب إجراء هذا التكامل قبل مكاملة الدالة بالنسبة لy. لاحظ أننا في البدء نعتبر y ثابتاً حيث أنها ليست متغير التكامل.

\begin{array}{l} \int_{11}^{14} (x^{2} + 4 y) d x & = (\frac{1}{3} x^{3} + 4 y x) |_{x = 11}^{x = 14} \\ = \frac{1}{3} (14)^{3} + 4 y (14) - \frac{1}{3} (11)^{3} - 4 y (11) \\ = 471 + 12 y \end{array}

بعد ذلك نكامل بالنسبة ل y

\begin{array}{l} \int_{7}^{10} (471 + 12 y) d y & = (471 y + 6 y^{2}) |_{y = 7}^{y = 10} \\ = 471 (10) + 6 (10)^{2} - 471 (7) - 6 (7)^{2} \\ = 1719 \end{array}

الحجوم

حجم متوازي المستطيلات ذو الأضلاع 4×6×5 نتحصل عليه بطريقتين:

التكامل الثنائي:: $\iint_{D} 5 d x d y$

للدالة 5=(f(x,y محسوبة في المنطقة D من مستوى xy الذي يمثل قاعدة متوازي المستطيلات:: $∭_{p a r a l l e l e p i p e d} 1 d x d y d z$

التكامل الثلاثي:: $∭_{p a r a l l e l e p i p e d} 1 d x d y d z$

للدالة الثابتة 1 محسوبةً على متوازي المستطيلات نفسه.

حساب الحجوم

بفضل الطرق المفصلة أعلاه يمكن تبيين قيمة الحجم لبعض الأجسام:

الأسطوانة: اعتبر أن المجال هو القاعدة الدائرية ذات نصف قطر R، والدالة ثابتة بالارتفاع h. يمكن كتابة ذلك في إحداثيات قطبية كالآتي:

V o l u m e = \int_{0}^{2 π} d ϕ \int_{0}^{R} h ρ d ρ = h 2 π {[\frac{ρ^{2}}{2}]}_{0}^{R} = π R^{2} h

التحقق: الحجم = مساحة القاعدة* الارتفاع=

π R^{2} \cdot h

الكرة: وهو توضيح جاهز لتطبيق التمرير في احداثيات كروية للدالة الثابتة المُكامَلة 1 في الكرة ذات نفس نصف القطر R:

V o l u m e = \int_{0}^{2 π} d ϕ \int_{0}^{π} \sin θ d θ \int_{0}^{R} ρ^{2} d ρ = 2 π \int_{0}^{π} \sin θ \frac{R^{3}}{3} d θ = \frac{2}{3} π R^{3} [- \cos θ]_{0}^{π} = \frac{4}{3} π R^{3} .

رباعي السطوح(هرم مثلثي ذو 4 وجوه): حجم رباعي سطوح ذو رأس عند نقطة الأصل يمكن حسابهعن طريق صيغ الاختزال آخذين بالاعتبار، كمثال، ال normality على المستوى xy ولمحور x ومثل الدالة الثابتة 1.

V o l u m e = \int_{0}^{ℓ} d x \int_{0}^{ℓ - x} d y \int_{0}^{ℓ - x - y} d z = \int_{0}^{ℓ} d x \int_{0}^{ℓ - x} (ℓ - x - y) d y

= \int_{0}^{ℓ} (ℓ^{2} - 2 ℓ x + x^{2} - \frac{(ℓ - x)^{2}}{2}) d x = ℓ^{3} - ℓ ℓ^{2} + \frac{ℓ^{3}}{3} - {[\frac{ℓ^{2}}{2} - ℓ x + \frac{x^{2}}{2}]}_{0}^{ℓ} =

= \frac{ℓ^{3}}{3} - \frac{ℓ^{3}}{6} = \frac{ℓ^{3}}{6}

التحقق: الحجم = مساحة القاعدة * الارتفاع /3 =

\frac{ℓ^{2}}{2} \cdot ℓ / 3 = \frac{ℓ^{3}}{6} .

التكامل المعتل المتعدد

في حالة المجالات غير المحدودة أو الدوال غير المحدودة بالقرب من حدود المجال، نقوم باستعمال التكامل المعتل الثنائي أو التكامل المعتل الثلاثي.

التكامل المعتل المتعدد والتكامل المتتابع

حسب مبرهنة فوبيني Fubini's theorm :

\int_{A \times B} | f (x, y) | d (x, y) < \infty,

هذا يعني أنه إذا كان التكامل محدد مطلقاً فان نفس النتيجة التي نحصل عليها بالتكامل المتعدد يمكن الحصول عليها بالتكامل المتتابع،: $\int_{A \times B} f (x, y) d (x, y) = \int_{A} (\int_{B} f (x, y) d y) d x = \int_{B} (\int_{A} f (x, y) d x) d y .$

يحدث ذلك تحديدا عندما تكون |(f(x,y| دالة محددة، وA وB مجموعتان محددتان. إذا لم يكن التكامل متقارب مطلقاً يجب العناية وعدم خلط مبادئ التكامل المتعدد والتكامل المتتابع، خاصة أن كلاهما يكتب بنفس الرموز. الرمز:

\int_{0}^{1} \int_{0}^{1} f (x, y) d y d x

يعني في بعض الحالات تكاملاً متتابعاً وليس تكاملاً ثنائياً حقيقياً. التكامل الخارجي في التكامل المتتابع: $\int_{0}^{1} \dots d x$

هو تكامل باعتبار x لدالة x التالية: $g (x) = \int_{0}^{1} f (x, y) d y .$

من ناحية أخرى، التكامل الثنائي يعرف باعتبار المساحة في المستوى xy. إذا وُجد تكامل ثنائي فانه يكون مساوياً لكل من التكاملين المتتابعين على حدا (إما "dy dx" أو"dx dy") ويتم حسابه عادة بحساب أحد التكاملين المتتابعين. ولكن أحياناً يوجد التكاملين المتتابعين إذا وفقط إذا لم يكن هناك تكامل ثنائي، ويكونان في هذه الجالة ذوي قيم متغايرة عن بعضهما كما في المثال:

\int_{0}^{1} \int_{0}^{1} f (x, y) d y d x \neq \int_{0}^{1} \int_{0}^{1} f (x, y) d x d y .

وهو إعادة ترتيب افتراضي للتكامل المتقارب شرطياً. نكتب: $\int_{[0, 1] \times [0, 1]} f (x, y) d x d y$

الذي يمكن استعماله للتأكد من أننا حسبنا التكامل المتعدد وليس المتتابع

بعض التطبيقات العملية

تستخدم هذه التكاملات في العديد من التطبيقات الفيزيائية

في الميكانيكا، يحسب عزم القصور الذاتي كتكامل حجم (تكامل ثلاثي) للكثافة الموزونة مع مربع المسافة من المحور:

I_{z} = ∭_{V} ρ r^{2} d V .

في الكهرومغناطيسية، يمكن كتابة معادلات ماكسويل في صورة تكامل ثلاثي لحساب المجالات الكهربية والمغناطيسية الكلية

فس المثال التالي حصلنا على المجال الكهربي بتوزيع للشحنات تم الحصول عليه عن طريق تكامل ثلاثي لدالة متجهة: $\vec{E} = \frac{1}{4 π ϵ_{0}} ∭ \frac{\vec{r} - {\vec{r}}^{'}}{{‖ \vec{r} - {\vec{r}}^{'} ‖}^{3}} ρ ({\vec{r}}^{'}) d^{3} r^{'} .$

انظر أيضًا

مبرهنات التحليل الرئيسية المرتبطة بالتكامل المتعدد:

مراجع

^ ^أ ^ب ميشال إبراهيم ورامي أبو سليمان وفادي (1 يناير 2007). Dictionaire des termes scientifiques (Anglais/Français/Arabe): قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي. Dar Al Kotob Al Ilmiyah دار الكتب العلمية. ISBN:978-2-7451-5445-3. مؤرشف من الأصل في 2020-02-20.
^ Larson؛ Edwards (2014). Multivariable Calculus (ط. 10th). Cengage Learning. ISBN:978-1-285-08575-3.
^ Rudin، Walter. Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (ط. 3rd). McGraw–Hill. ISBN:978-0-07-054235-8. مؤرشف من الأصل في 2019-03-25.
^ Stewart، James (2008). Calculus: Early Transcendentals (ط. 6th). Brooks Cole Cengage Learning. ISBN:978-0-495-01166-8. مؤرشف من الأصل في 2019-12-15.

Robert A. Adams - Calculus: A Complete Course (5th Edition) ISBN 0-201-79131-5.

بوابة تحليل رياضي

[Dict-1] أ ^ب ميشال إبراهيم ورامي أبو سليمان وفادي (1 يناير 2007). Dictionaire des termes scientifiques (Anglais/Français/Arabe): قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي. Dar Al Kotob Al Ilmiyah دار الكتب العلمية. ISBN:978-2-7451-5445-3. مؤرشف من الأصل في 2020-02-20.

[2] Larson؛ Edwards (2014). Multivariable Calculus (ط. 10th). Cengage Learning. ISBN:978-1-285-08575-3.

[3] Rudin، Walter. Principles of Mathematical Analysis. Walter Rudin Student Series in Advanced Mathematics (ط. 3rd). McGraw–Hill. ISBN:978-0-07-054235-8. مؤرشف من الأصل في 2019-03-25.

[Stewart-4] Stewart، James (2008). Calculus: Early Transcendentals (ط. 6th). Brooks Cole Cengage Learning. ISBN:978-0-495-01166-8. مؤرشف من الأصل في 2019-12-15.

[1]

[2]

[3]

[4]

ع ن ت مواضيع التفاضل والتكامل
ما قبل حساب التفاضل والتكامل ^[English]	مبرهنة ذي الحدين دوال خطيَّة مُستمِرة مُقعَّرة العاملي فرق محدود المتغير الحر والمتغير المقيد تمثيل الدالة البياني ميل المستقيم راديان مبرهنة رول القاطع المماس
النهايات	صيغة غير مُحدَّدة نهاية دالة وحيدة الجانب نهاية متتالية درجة التقريب
حساب التفاضل	مُشتَق تفاضلي ^[English] معادلة تفاضلية مؤثر تفاضلي مبرهنة القيمة المتوسطة تدوين التفاضل ^[English] لايبنز نيوتن ^[English] قواعد التفاضل الخطيَّة الرفع إلى أُس السلسلة لوبيتال الضرب قاعدة لايبنيز العامة ناتج القسمة تقنيات أخرى الدوال العكسية اللوغاريتم المعدلات المرتبطة نقاط الثبات اختبار المشتق مبرهنة القيمة المُتَّطرفة النقاط الحدية تطبيقات أُخرى طريقة نيوتن لإيجاد الجذور سلسلة تايلور
حساب التكامل	المبرهنة الأساسية مُشتَق التكامل ثابت التكامل بالتجزئة بالتعويض مُثلثي أويلر ^[English] فايرشتراس ^[English] تربيعي ^[English] شبه المنحرف مُشتَق عكسي طول القوس الحجوم بالأقراص بالطبقات الأسطوانية
حساب المتجهات	مشتق اتجاهي المؤثرات دوران تباعد تدرج لابلاس مبرهنات رئيسة التدرُّج التباعد غرين كلفن وستوكس
حساب التفاضل والتكامل متعدد المتغيرات	مبرهنة التباعد حساب المصفوفات حساب هندسي ياكوبية هيسية معامل لاغرانج تكاملات خط سطح حجم متعدد مشتق جزئي مواضيع مُتقدِّمة أشكال تفاضلية مشتق خارجي مبرهنة ستوكس المُعمَّمة حساب المُوتِّر
المتتاليات والسلاسل	متتالية حسابية هندسية ^[English] أنواع السلاسل متناوبة ذات حدين فورييه هندسية متناسقة قوى تايلور متداخلة اختبارات التقارب أبيل ^[English] السلاسل المتناوبة ^[English] كوشي للتكثيف ^[English] المقارنة المباشرة ^[English] دركليه التكامل ^[English] مقارنة النهايات ^[English] النسبة الأصل ^[English] الحد النوني
دوال وأرقام مُميَّزة	أعداد برنولي ثابت أويلر دالة أسية لوغاريتم طبيعي تقريب ستيرلينغ
تاريخ التفاضل والتكامل	شخصيات تايلور ماكلورين لايبنتس نيوتن أويلر مفاهيم تسوية ^[English] المتناهيات في الصغر التدفق قانون الاستمرارية ^[English] عمومية الجبر ^[English] كتب طريقة المبرهنات الميكانيكية طرق التدفق
قوائم	قواعد التفاضل تكاملات الدوال اللوغاريتمية الأسية المثلثية العكسية القواطع ^[English] المُكعَّبة ^[English] الزائدية العكسية الكسرية غير الكسرية النهايات
مواضيع متنوعة	الانحناء هندسة تفاضلية للمنحنيات للسطوح ^[English] صيغة أويلر وماكلورين بوق جبريل إثبات أن 22/7 أكبر من π مسألة ريغيومونتانوس للزاوية العظمى ^[English] مجسم شتاينميتز ^[English]
تصنيف • كومنز بوابة رياضيات • بوابة تحليل رياضي • بوابة هندسة رياضية

تكامل متعدد

محتويات

مقدمة

التعريف الرياضي

الخصائص

حالات خاصة

طرق للتكامل

الحل المباشر

الدوال الثابتة

الحل باستخدام التماثل

صيغ الاختزال

المجالات البسيطة على R²

محور x

محور y

مثال

المجالات البسيطة على R³

تغيير المتغيرات

الإحداثيات القطبية

الإحداثيات الأسطوانية

الإحداثيات الكروية

أمثلة

التكامل الثنائي

الحجوم

حساب الحجوم

التكامل المعتل المتعدد

التكامل المعتل المتعدد والتكامل المتتابع

بعض التطبيقات العملية

انظر أيضًا

مراجع

قائمة التصفح

تكامل متعدد

مقدمة

التعريف الرياضي

الخصائص

حالات خاصة

طرق للتكامل

الحل المباشر

الدوال الثابتة

الحل باستخدام التماثل

صيغ الاختزال

المجالات البسيطة على R2

محور x

محور y

مثال

المجالات البسيطة على R3

تغيير المتغيرات

الإحداثيات القطبية

الإحداثيات الأسطوانية

الإحداثيات الكروية

أمثلة

التكامل الثنائي

الحجوم

حساب الحجوم

التكامل المعتل المتعدد

التكامل المعتل المتعدد والتكامل المتتابع

بعض التطبيقات العملية

انظر أيضًا

مراجع

قائمة التصفح

بحث

المجالات البسيطة على R²

المجالات البسيطة على R³