تأثير صوتي مرن

تأثير صوتي مرن (بالإنجليزية: Acoustoelastic effect)‏، وهو تفسير كيفية تغير سرعات موجات الصوت (سواء الموجات الطولية وسرعات موجات القص) لمادة مرنة إذا تعرضت لحقل إجهاد ثابت أولي. هذا تأثير غير خطي للعلاقة التأسيسية بين الإجهاد الميكانيكي والانفعال المحدود في مادة ذات كتلة مستمرة. في نظرية المرونة الخطية الكلاسيكية، يمكن وصف التشوهات الصغيرة لمعظم المواد المرنة بعلاقة خطية بين الإجهاد المطبق والسلالة الناتجة. تُعرف هذه العلاقة عمومًا باسم قانون هوك المعمم. تتضمن نظرية المرونة الخطية ثوابت مرنة من الدرجة الثانية (على سبيل المثال $λ$ و $μ$ ) وتنتج سرعات صوت طولية وقص ثابتة في مادة مرنة، لا تتأثر بضغط مطبق. من ناحية أخرى، يشمل التأثير الصوتي المرن توسعًا عالي المستوى للعلاقة التأسيسية (نظرية المرونة غير الخطية ^[1] ) بين الضغط المطبق والضغط الناتج، والذي ينتج سرعات صوت طولية وسرعات قص تعتمد على حالة إجهاد المادة. في حدود مادة غير مضغوطة، يتم إعادة إنتاج سرعات الصوت لنظرية المرونة الخطية.

تم التحقيق في التأثير الصوتي المرن في وقت مبكر من عام 1925 بواسطة بريلوين.^[2] وجد أن سرعة انتشار الموجات الصوتية ستنخفض بالتناسب مع الضغط الهيدروستاتيكي المطبق. ومع ذلك، كانت نتيجة نظريته أن الموجات الصوتية ستتوقف عن الانتشار عند ضغط كبير بدرجة كافية. تبين لاحقًا أن هذا التأثير المتناقض ناتج عن الافتراضات غير الصحيحة بأن المعلمات المرنة لم تتأثر بالضغط.^[3]

في عام 1937، قدم مورناغان ^[4] نظرية رياضية توسع من نظرية المرونة الخطية لتشمل أيضًا التشوه المحدود في المواد الخواص المرنة. تضمنت هذه النظرية ثلاثة ثوابت مرنة من الدرجة الثالثة $l$ و $m$ ، و $n$ . في عام 1953 استخدم هاجز وكيلي نظرية مورناغان في عملهم تجريبي لتحديد القيم العددية لأعلى أجل الثوابت المرنة لعدة مواد مرنة بما في ذلك البوليستيرين، شركة أرامكو الحديد، و بيركس، تعرض لل ضغط الهيدروستاتيكي والضغط أحادي المحور.^[5]

نظرية المرونة غير الخطية للمواد فائقة المرونة

التأثير الصوتي هو تأثير التشوه المحدود للمواد المرنة غير الخطية. يمكن العثور على حساب شامل حديث لهذا في.^[1] يعالج هذا الكتاب تطبيق نظرية المرونة غير الخطية وتحليل الخواص الميكانيكية للمواد الصلبة القادرة على إحداث تشوهات مرنة كبيرة. الحالة الخاصة لنظرية المرونة الصوتية لمادة مفرطة المرونة قابلة للانضغاط، مثل الفولاذ متعدد البلورات ^[6] يتم إعادة إنتاجها وعرضها في هذا النص من نظرية المرونة غير الخطية كما قدمها أوجدن.^[1]

لاحظ أن الإعداد في هذا النص وكذلك في ^[1] متساوي الحرارة، ولا توجد إشارة إلى الديناميكا الحرارية .

العلاقة التأسيسية - المواد مفرطة المرونة (علاقة الإجهاد والانفعال)

المادة المفرطة المرونة هي حالة خاصة لمادة كوشي المرنة حيث يكون الضغط في أي نقطة موضوعيًا ويتم تحديده فقط من خلال الحالة الحالية للتشوه فيما يتعلق بتكوين مرجعي عشوائي (لمزيد من التفاصيل حول التشوه، انظر أيضًا الصفحات تشوه (الميكانيكا ) وسلالة محدودة ). ومع ذلك، قد يعتمد العمل الذي تقوم به الضغوط على المسار الذي يتخذه التشوه. لذلك، فإن مادة كوشي المرنة لها هيكل غير متحفظ، ولا يمكن اشتقاق الضغط من دالة محتملة مرنة قياسية. يشار إلى الحالة الخاصة لمواد كوشي المرنة حيث يكون العمل الذي تقوم به الضغوط مستقلًا عن مسار التشوه مادة خضراء مرنة أو مادة فائقة المرونة. هذه المواد متحفظة ويمكن اشتقاق الضغوط الموجودة في المادة بواسطة جهد مرن قياسي، يُعرف أكثر باسم دالة كثافة طاقة الإجهاد.

يمكن التعبير عن العلاقة التأسيسية بين الإجهاد والانفعال بأشكال مختلفة بناءً على أشكال الإجهاد والتوتر المختارة. اختيار موتر الإجهاد الميكانيكي لبيولا كيرشوف الأول $P$ (وهو تبديل موتر الإجهاد الاسمي $P^{T} = N$ )، يمكن التعبير عن المعادلة التأسيسية لمادة مرنة شديدة الانضغاط بدلالة سلالة لاغرانج جرين ( $E$ ) كما:

$P = F \cdot \frac{\partial W}{\partial E} or P_{i j} = F_{i k} \frac{\partial W}{\partial E_{k j}}, i, j = 1, 2, 3,$

حيث $F$ هو موتر التدرج التشوهي، وحيث يستخدم التعبير الثاني اصطلاح جمع آينشتاين لتدوين مؤشر التوتر . $W$ هي دالة كثافة طاقة الإجهاد لمادة مفرطة المرونة وقد تم تحديدها لكل وحدة حجم وليس لكل وحدة كتلة لأن هذا يتجنب الحاجة إلى مضاعفة الجانب الأيمن مع كثافة الكتلة $ρ_{0}$ من التكوين المرجعي.^[1]

بافتراض أن دالة كثافة طاقة السلالة العددية $W (E)$ يمكن تقريبه عن طريق توسع سلسلة تايلور في السلالة الحالية $E$ ، يمكن التعبير عنها (في تدوين الفهرس) على النحو التالي:

$W \approx C_{0} + C_{i j} E_{i j} + \frac{1}{2!} C_{i j k l} E_{i j} E_{k l} + \frac{1}{3!} C_{i j k l m n} E_{i j} E_{k l} E_{m n} + \dots$

فرض القيود على أن وظيفة طاقة الإجهاد يجب أن تكون صفرية ولها حد أدنى عندما تكون المادة في حالة غير مشوهة (أي $W (E_{i j} = 0) = 0$ ) من الواضح أنه لا يوجد حد ثابت أو خطي في دالة طاقة الإجهاد، وبالتالي:

$W \approx \frac{1}{2!} C_{i j k l} E_{i j} E_{k l} + \frac{1}{3!} C_{i j k l m n} E_{i j} E_{k l} E_{m n} + \dots,$

حيث $C_{i j k l}$ هو موتر من الدرجة الرابعة لوحدات مرنة من الدرجة الثانية، بينما $C_{i j k l m n}$ هو موتر من الدرجة السادسة لمعايير مرنة من الدرجة الثالثة. تناظر $E_{i j} = E_{j i}$ جنبًا إلى جنب مع دالة كثافة طاقة السلالة العددية $W$ يعني أن معاملات الدرجة الثانية $C_{i j k l}$ لديك التناظر التالي:

$C_{i j k l} = C_{j i k l} = C_{i j l k},$

مما يقلل من عدد الثوابت المرنة المستقلة من 81 إلى 36. بالإضافة إلى ذلك، فإن تمدد القوة يعني أن معايير الدرجة الثانية لها أيضًا تناظر كبير

$C_{i j k l} = C_{k l i j},$

مما يقلل من عدد الثوابت المرنة المستقلة إلى 21. يمكن استخدام نفس الوسيطات لمعايير المرونة من الدرجة الثالثة $C_{i j k l m n}$ . تسمح هذه التناظرات أيضًا بالتعبير عن المعاملات المرنة بواسطة تدوين Voigt (أي $C_{i j k l} = C_{I J}$ و $C_{i j k l m n} = C_{I J K}$ ).

يمكن التعبير عن موتر التدرج المشوه في شكل مكون على النحو التالي

$F_{i j} = \frac{\partial u_{i}}{\partial X_{j}} + δ_{i j},$

حيث $u_{i}$ هو إزاحة نقطة مادية $P$ من تنسيق $X_{i}$ في التكوين المرجعي للتنسيق $x_{i}$ في التكوين المشوه (انظر الشكل 2 في صفحة نظرية السلالة المحدودة). بما في ذلك تمدد القوة لوظيفة طاقة الإجهاد في العلاقة التأسيسية واستبدال موتر الإجهاد اللاغرانج $E_{k l}$ مع التمدد المعطى على نتائج صفحة موتر الإجهاد المحدودة (لاحظ أن الأحرف الصغيرة $u$ تم استخدامها في هذا القسم مقارنة بالحالة الكبيرة في صفحة الإجهاد المحدود ) المعادلة التأسيسية

$P_{i j} = C_{i j k l} \frac{\partial u_{k}}{\partial X_{l}} + \frac{1}{2} M_{i j k l m n} \frac{\partial u_{k}}{\partial X_{l}} \frac{\partial u_{m}}{\partial X_{n}} + \frac{1}{3} M_{i j k l m n p q} \frac{\partial u_{k}}{\partial X_{l}} \frac{\partial u_{m}}{\partial X_{n}} \frac{\partial u_{p}}{\partial X_{q}} + \dots,$

حيث

$M_{i j k l m n} = C_{i j k l m n} + C_{i j l n} δ_{k m} + C_{j n k l} δ_{i m} + C_{j l m n} δ_{i k},$

ومصطلحات الرتبة الأعلى تم إهمالها ^[7]^[8] (انظر ^[9] للحصول على الاشتقاقات التفصيلية). للرجوع إليها عن طريق إهمال شروط الترتيب الأعلى في $\partial u_{k} / \partial X_{l}$ هذا التعبير يقلل إلى $P_{i j} = C_{i j k l} \frac{\partial u_{k}}{\partial X_{l}},$ وهو نسخة من قانون هوك المعمم حيث $P_{i j}$ هو مقياس للضغط أثناء $\partial u_{k} / \partial X_{l}$ هو مقياس للضغط، و $C_{i j k l}$ هي العلاقة الخطية بينهما.

سرعة الصوت

بافتراض أن تشوهًا ديناميكيًا صغيرًا (صوتيًا) يزعج مادة مضغوطة بشكل ثابت بالفعل، يمكن اعتبار تأثير المرونة الصوتية تأثيرًا على تشوه صغير متراكب على تشوه محدود أكبر (يُطلق عليه أيضًا نظرية صغيرة على كبيرة).^[8] دعونا نحدد ثلاث حالات لنقطة مادية معينة. في الحالة المرجعية (غير المشددة) يتم تحديد النقطة بواسطة متجه الإحداثيات $X$ بينما نفس النقطة لها متجه الإحداثيات $x$ في حالة الإجهاد الثابت في البداية (أي تحت تأثير الإجهاد المسبق المطبق). أخيرًا، افترض أن النقطة المادية الواقعة تحت اضطراب ديناميكي صغير (مجال الضغط الصوتي) لها متجه الإحداثيات $x^{'}$ . يمكن بعد ذلك وصف الإزاحة الكلية لنقاط المواد (تحت تأثير كل من الإجهاد المسبق الثابت والاضطراب الصوتي الديناميكي) بواسطة نواقل الإزاحة

$u = u^{(0)} + u^{(1)} = x^{'} - X,$

حيث

$u^{(0)} = x - X, u^{(1)} = x^{'} - x$

يصف الإزاحة الأولية الساكنة (لاغرانج) بسبب الإجهاد المسبق المطبق، والإزاحة (أويلريان) بسبب الاضطراب الصوتي، على التوالي. قانون كوشي الأول للحركة (أو توازن الزخم الخطي) لاضطراب أويلريان الإضافي $u^{(1)}$ يمكن بعد ذلك اشتقاقها من حيث التشوه الوسيط لاغرانج $u^{(0)}$ على افتراض أن الافتراض الصغير مقابل الكبير

$| u^{(1)} | ≪ | u^{(0)} |$

يحمل. استخدام صيغة لاغرانج لقانون كوشي الأول للحركة، حيث تم إهمال تأثير قوة الجسم الثابتة (أي الجاذبية)، ينتج عنه

$D i v P = ρ_{0} \ddot{{x^{'}}^{'}} .$

لاحظ أنه يتم استخدام الرمز "0" المنخفض / المرتفع في هذا النص للإشارة إلى حالة المرجع غير المشدد، وأن المتغير المنقط هو الوقت المعتاد ( $t$ ) مشتق المتغير $D i v$ هو عامل الاختلاف فيما يتعلق بنظام إحداثيات لاغرانج $X$ .

يمكن التعبير عن الجانب الأيمن (الجزء المعتمد على الوقت) من قانون الحركة كـ

$\begin{array}{r} ρ_{0} \ddot{{x^{'}}^{'}} & = ρ_{0} \frac{\partial^{2}}{\partial t^{2}} (u^{(0)} + u^{(1)} + X) \\ = ρ_{0} \frac{\partial^{2} u^{(1)}}{\partial t^{2}} \end{array}$

على افتراض أن كلا من حالة عدم الإجهاد وحالة التشوه الأولية ثابتة وبالتالي

$\partial^{2} / \partial t^{2} (u^{(0)}) = \partial^{2} / \partial t^{2} (X) = 0$ .

بالنسبة للجانب الأيسر (الجزء المعتمد على الفضاء)، مشتقات لاغرانج الجزئية المكانية بالنسبة إلى $X_{j}$ يمكن توسيعها في أويلريان $x_{j}$ باستخدام قاعدة السلسلة وتغيير المتغيرات من خلال العلاقة بين متجهات الإزاحة على النحو ^[8]

$\frac{\partial}{\partial X_{j}} = \frac{\partial}{\partial x_{j}} + u_{k, j}^{(0)} \frac{\partial}{\partial x_{k}} + \dots$

حيث الشكل القصير $u_{k, j}^{(0)} \equiv \partial u_{k}^{(0)} / \partial x_{j}$ تم استخدامه. هكذا

$\frac{\partial P_{i j}}{\partial X_{j}} \approx \frac{\partial P_{i j}}{\partial x_{j}} + u_{p . j}^{(0)} \frac{\partial P_{i j}}{\partial x_{p}}$

على افتراض كذلك أن التشوه الأولي الثابت $u^{(0)}$ (حالة الإجهاد المسبق) في حالة توازن يعني ذلك $D i v P^{(0)} = 0$ ، ويمكن لقانون الحركة بالاقتران مع المعادلة التأسيسية المذكورة أعلاه أن يختزل إلى علاقة خطية (أي عندما تكون شروط الترتيب الأعلى في $u_{m, n}^{(0)}$ ) بين التشوه الأولي الثابت $u^{(0)}$ والاضطراب الديناميكي الإضافي $u^{(1)} (x, t)$ مثل ^[7] (انظر ^[9] للحصول على الاشتقاقات التفصيلية)

$B_{i j k l} \frac{\partial^{2} u_{k}^{(1)}}{\partial x_{j} \partial x_{l}} = ρ_{0} \frac{\partial^{2} u_{i}^{(1)}}{\partial t^{2}},$

حيث

$B_{i j k l} = C_{i j k l} + δ_{i k} C_{j l q r} u_{q, r}^{(0)} + C_{r j k l} u_{i, r}^{(0)} + C_{i r k l} u_{j, r}^{(0)} + C_{i j r l} u_{k, r}^{(0)} + C_{i j k r} u_{l, r}^{(0)} + C_{i j k l m n} u_{m, n}^{(0)} .$

يتم التعرف على هذا التعبير على أنه معادلة الموجة الخطية . النظر في موجة مستوية من النموذج

$u^{(1)} (x, t) = m f (N \cdot x - c t),$

حيث $N$ هو متجه وحدة لاغرانج في اتجاه الانتشار (أي موازٍ لرقم الموجة $k = k N$ طبيعي في مقدمة الموجة،)، $m$ هو متجه وحدة يشار إليه باسم متجه الاستقطاب (يصف اتجاه حركة الجسيمات)، $c$ هي سرعة موجة الطور، و $f$ هي وظيفة قابلة للتفاضل مرتين بشكل مستمر (على سبيل المثال وظيفة جيبية ). إدخال هذه الموجة المستوية في معادلة الموجة الخطية المشتقة أعلاه النتائج ^[10]

Q (N) m = ρ_{0} c^{2} m

حيث $Q (N)$ يتم تقديمه على أنه موتر صوتي، ويعتمد على $N$ كـ ^[10]

$[Q (N)]_{i k} = B_{i j k l} N_{j} N_{l} .$

يسمى هذا التعبير بشرط الانتشار ويحدد اتجاه انتشار معين $n$ سرعة واستقطاب الموجات المحتملة المقابلة للموجات المستوية. يمكن تحديد سرعات الموجة بواسطة المعادلة المميزة ^[10]

$det (Q (N) - ρ_{0} c^{2} I) = 0,$

حيث $det$ هو المحدد و $I$ هي مصفوفة الهوية .

لمواد مفرطة المرونة $Q (N)$ متماثل (ولكن ليس بشكل عام)، والقيم الذاتية ( $ρ_{0} c^{2}$ ) حقيقية. لكي تكون سرعات الموجة حقيقية أيضًا، يجب أن تكون القيم الذاتية موجبة.^[1] إذا كانت هذه هي الحالة، توجد ثلاث موجات مستوية حقيقية متعامدة متبادلة لاتجاه الانتشار المحدد $N$ . من تعبيري الموتر الصوتي، من الواضح أن ^[10]

$ρ_{0} c^{2} = Q (N) m \cdot m = B_{i j k l} N_{j} N_{l} m_{i} m_{k},$

وعدم المساواة $B_{i j k l} N_{j} N_{l} m_{i} m_{k} > 0$ (وتسمى أيضًا حالة الإهليلجية القوية) لجميع النواقل غير الصفرية $N$ و $m$ تضمن أن تكون سرعة الموجات المستوية المتجانسة حقيقية. الاستقطاب $m = N$ يتوافق مع موجة طولية حيث تكون حركة الجسيم موازية لاتجاه الانتشار (يشار إليها أيضًا باسم الموجة الانضغاطية). الاستقطابين حيث $m \cdot N = 0$ يتوافق مع الموجات المستعرضة حيث تكون حركة الجسيمات متعامدة مع اتجاه الانتشار (يشار إليها أيضًا باسم موجات القص).^[10]

تماثل المواد

نماذج مرنة للمواد المتماثلة

بالنسبة إلى موتر الخواص من الدرجة الثانية (أي موتر له نفس المكونات في أي نظام إحداثيات) مثل موتر إجهاد لاغرانج $E$ لديك الثوابت $t r E^{q}$ حيث $t r$ هو عامل التتبع، و $q \in {1, 2, 3, \dots}$ . وبالتالي يمكن التعبير عن وظيفة طاقة الإجهاد لمادة الخواص $W (E) = W (t r E^{q}), k \in {1, 2, 3, \dots}$ ، أو تراكب هناك، والذي يمكن إعادة كتابته كـ ^[8]

$W = \frac{λ}{2} (t r E)^{2} + μ t r E^{2} + \frac{C}{3} (t r E)^{3} + B (t r E) t r E^{2} + \frac{A}{3} t r E^{3} + \dots,$

حيث $λ, μ, A, B, C$ هي ثوابت. الثوابت $λ$ و $μ$ هي المعامل المرنة من الدرجة الثانية المعروفة باسم معلمات لامي، بينما $A, B,$ و $C$ هي المقاييس المرنة من الدرجة الثالثة التي تم تقديمها بواسطة، ^[11] والتي تعتبر بديلة ولكنها مكافئة لها $l, m,$ و $n$ قدمه مورناغان.^[4] بدمج هذا مع التعبير العام لوظيفة طاقة الإجهاد، من الواضح أن ^[8]

$\begin{array}{r} C_{i j k l} & = λ δ_{i j} δ_{k l} + 2 μ δ I_{i j k l}, \\ C_{i j k l m n} & = 2 C δ_{i j} δ_{k l} δ_{m n} + 2 B (δ_{i j} I_{k l m n} + δ_{k l} I_{m n i j} + δ_{m n} I_{i j k l}) + \frac{1}{2} A (δ_{i k} I_{j l m n} + δ_{i l} I_{j k m n} + δ_{j k} I_{i l m n} + δ_{j l} I_{i k m n}), \end{array}$

حيث $I_{i j k l} = \frac{1}{2} (δ_{i k} δ_{j l} + δ_{i l} δ_{j k})$ . تم استخدام اختيار مختلف تاريخيًا لهذه الثوابت المرنة من الدرجة الثالثة، وتظهر بعض الاختلافات في الجدول 1.

**الجدول 1:** العلاقة بين الثوابت المرنة من الدرجة الثالثة للمواد الصلبة الخواص ^[7]
لانداو وليفشيتز (1986) ^[11]	توبين وبرنشتاين (1961) ^[12]	مورناغان (1951) ^[4]	بلاند (1969) ^[13]	إرينجن وسوهوبي (1974) ^[14]	اساسي $C_{I J K}$
$A$	$ν_{1} = 2 C$	$l = B + C$	$α = \frac{1}{3} C$	$l_{E} = \frac{1}{3} A + B + \frac{1}{3} C$	$C_{123} = 2 C$	$C_{111} = 2 A + 6 B + 2 C$
$B$	$ν_{2} = B$	$m = \frac{1}{2} A + B$	$β = B$	$m_{E} = - A - 2 B$	$C_{144} = B$	$C_{112} = 2 B + 2 C$
$C$	$ν_{3} = \frac{1}{4} A$	$n = A$	$γ = \frac{1}{3} A$	$n_{E} = A$	$C_{456} = \frac{1}{4} A$	$C_{166} = \frac{1}{2} A + B$

أمثلة للصلب

يقدم الجدولان 2 و 3 الثوابت المرنة من الرتبة الثانية والثالثة لبعض أنواع الصلب الواردة في الأدبيات

**الجدول 2:** ثوابت لامي وتوبين وبيرنشتاين في GPa
	ثوابت لامي		ثوابت توبين وبرنشتاين
مادة	$λ$	$μ$	$ν_{1}$	$ν_{2}$	$ν_{3}$
هيكلا 37 (0.4٪ ج) ^[15]	$111 \pm 1$	$82.1 \pm 0.5$	$- 385 \pm 70$	$- 282 \pm 30$	$- 177 \pm 8$
هيكلا 37 (0.6٪ ج) ^[15]	$110.5 \pm 1$	$82.0 \pm 0.5$	$- 134 \pm 20$	$- 261 \pm 20$	$- 167 \pm 6$
هيكلا 138 أ ^[15]	$109 \pm 1$	$81.9 \pm 0.5$	$- 323 \pm 50$	$- 265 \pm 30$	$- 177 \pm 10$
ريكس 535 ني فولاذ ^[15]	$109 \pm 1$	$81.8 \pm 0.5$	$- 175 \pm 50$	$- 240 \pm 50$	$- 169 \pm 15$
هيكلا ATV الأوستنيتي ^[15]	$87 \pm 2$	$71.6 \pm 3$	$34 \pm 20$	$- 552 \pm 80$	$- 100 \pm 10$

**الجدول 3:** ثوابت لامي ومورناغان في GPa
	ثوابت لامي		ثوابت مورناغان
مادة	$λ$	$μ$	$l$	$m$	$n$
النيكل والصلب S / NVT ^[16]	$109.0 \pm 1$	$81.7 \pm 0.2$	$- 56 \pm 20$	$- 671 \pm 6$	$- 785 \pm 7$
عينة السكك الحديدية الفولاذية 1 ^[17]	$115.8 \pm 2.3 %$	$79.9 \pm 2.3 %$	$- 248 \pm 2.8 %$	$- 623 \pm 4.1 %$	$- 714 \pm 2.7 %$
عينة السكك الحديدية الفولاذية 4 ^[17]	$110.7 \pm 2.3 %$	$82.4 \pm 2.3 %$	$- 302 \pm 2.8 %$	$- 616 \pm 4.1 %$	$- 724 \pm 2.7 %$

المرونة الصوتية للتوتر أحادي المحور للمواد مفرطة المرونة الخواص

يمكن التعبير عن عينة مكعبة من مادة صلبة مضغوطة في تكوين مرجعي غير مضغوط بواسطة الإحداثيات الديكارتية $X_{i} \in [0, L_{i}], i = 1, 2, 3$ ، حيث تتم محاذاة الهندسة مع نظام الإحداثيات لاغرانج، و $L_{i}$ هو طول جوانب متوازي المستطيلات في التكوين المرجعي. تعرض المكعب للتوتر أحادي المحور في $x_{1}$ - الاتجاه بحيث يتشوه بسلالة متجانسة خالصة بحيث يمكن التعبير عن إحداثيات نقاط المواد في التكوين المشوه بواسطة $x_{1} = λ_{1} X_{1}, x_{2} = λ_{2} X_{2}, x_{3} = λ_{3} X_{3}$ ، مما يعطي الاستطالات

$e_{i} \equiv l_{i} / L_{i} - 1 = λ_{i} - 1$

في ال $x_{i}$ -اتجاه. هنا $l_{i}$ يشير إلى الطول الحالي (المشوه) للجانب متوازي المستطيلات $i$ وحيث يتم الإشارة إلى النسبة بين طول الجانبين في التكوين الحالي والمرجعي بواسطة

$λ_{i} \equiv l_{i} / L_{i}$

تسمى الامتدادات الرئيسية. بالنسبة إلى مادة متناحرة، يتوافق هذا مع تشوه بدون أي دوران (انظر التحلل القطبي لموتّر التدرج المشوه حيث $F = R U = V R$ والدوران $R = I$ ). يمكن وصف ذلك من خلال التمثيل الطيفي من خلال الامتدادات الرئيسية $λ_{i}$ كقيم ذاتية، أو مكافئ من خلال الاستطالات $e_{i}$ .

للتوتر أحادي المحور في $x_{1}$ -اتجاه ( $P_{11} > 0$ نفترض أن $e_{1}$ زيادة بمقدار ما. إذا كانت الوجوه الجانبية خالية من الجر (أي $P_{22} = P_{33} = 0$ ) الاستطالات الجانبية $e_{2}$ و $e_{3}$ تقتصر على النطاق $e_{2}, e_{3} \in (- 1, 0]$ . من أجل التناظر الخواص، يجب أن تكون الاستطالات الجانبية (أو الانقباضات) متساوية أيضًا (على سبيل المثال $e_{2} = e_{3}$ ). النطاق يتوافق مع النطاق من الانكماش الجانبي الكلي ( $e_{2} = e_{3} = - 1$ ، وهو غير مادي)، وبدون تغيير في الأبعاد الجانبية ( $e_{2} = e_{3} = 0$ ). ويلاحظ أنه من الناحية النظرية، يمكن توسيع النطاق إلى قيم أكبر من 0 تقابل زيادة في الأبعاد الجانبية نتيجة للزيادة في البعد المحوري. ومع ذلك، عدد قليل جدا من المواد (وتسمى منمي الحجم المواد) يحمل هذه الخاصية.

توسيع سرعات الصوت

إذا كانت حالة الإهليلجية القوية ( $B_{i j k l} N_{j} N_{l} m_{i} m_{k} > 0$ ) يحمل ثلاثة اتجاهات استقطاب متعامد ( $m$ سوف يعطي سرعة صوت غير صفرية وحقيقية لاتجاه انتشار معين $N$ . سيشتق ما يلي سرعات الصوت لاختيار واحد للشد أحادي المحور المطبق واتجاه الانتشار ومجموعة متعامدة من نواقل الاستقطاب. للتوتر أحادي المحور المطبق في $x_{1}$ -الاتجاه واشتقاق سرعات الصوت للموجات التي تنتشر بشكل متعامد مع التوتر المطبق (على سبيل المثال في $x_{3}$ -الاتجاه مع ناقل الانتشار $N = [0, 0, 1]$ )، قد يكون اختيار واحد من الاستقطابات المتعامدة

${m} = {\begin{matrix} m_{1} = {\hat{x}}_{1} = [1, 0, 0] & | to applied tension \\ m_{2} = {\hat{x}}_{2} = [0, 1, 0] & ⊥ to applied tension \\ m_{3} = {\hat{x}}_{3} = [0, 0, 1] & | to N \end{matrix}$

الذي يعطي سرعات الصوت الثلاث

$ρ_{0} c_{33}^{2} = B_{3333}, ρ_{0} c_{31}^{2} = B_{1313}, ρ_{0} c_{32}^{2} = B_{2323},$

حيث الفهرس الأول $i$ من سرعات الصوت $c_{i j}$ أشر إلى اتجاه الانتشار (هنا $x_{3}$ الاتجاه بينما الفهرس الثاني $j$ تشير إلى اتجاه الاستقطاب المحدد ( $j = i$ يتوافق مع حركة الجسيمات في اتجاه الانتشار $i$ - أي موجة طولية، و $j \neq i$ يتوافق مع حركة الجسيمات العمودية على اتجاه الانتشار - أي موجة القص).

توسيع المعاملات ذات الصلة للموتر الصوتي، واستبدال المعاملين المرنة من الرتبتين الثانية والثالثة $C_{i j k l}$ و $C_{i j k l m n}$ مع معادلاتها الخواص، $λ, μ$ و $A, B, C$ على التوالي، يؤدي إلى سرعات الصوت المعبر عنها كـ

$ρ_{0} c_{33}^{2} = λ + 2 μ + a_{33} e_{1}, ρ_{0} c_{3 k}^{2} = μ + a_{3 k} e_{1}, k = 1, 2$

حيث

a_{33} = - \frac{2 λ (λ + 2 μ) + λ A + 2 (λ - μ) B - 2 μ C}{λ + μ}

a_{31} = \frac{(λ + 2 μ) (4 μ + A) + 4 μ B}{4 (λ + μ)}

a_{32} = - \frac{λ (4 μ + A) - 2 μ B}{2 (λ + μ)}

هي معاملات المرونة الصوتية المرتبطة بالتأثيرات من الثوابت المرنة من الدرجة الثالثة.^[18]

طرق القياس

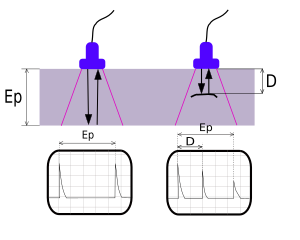
لتكون قادرًا على قياس سرعة الصوت، وبشكل أكثر تحديدًا التغيير في سرعة الصوت، في مادة تخضع لبعض حالات الإجهاد، يمكن للمرء قياس سرعة إشارة صوتية تنتشر عبر المادة المعنية. توجد عدة طرق للقيام بذلك ولكن جميعها تستخدم واحدة من علاقتين ماديتين لسرعة الصوت. تتعلق العلاقة الأولى بالوقت الذي تستغرقه الإشارة للانتشار من نقطة إلى أخرى (عادةً المسافة بين محولين صوتيين أو ضعف المسافة من محول طاقة إلى سطح عاكس). غالبًا ما يشار إلى هذا باسم قياسات "وقت الرحلة" (TOF)، واستخدم العلاقة

$c = \frac{d}{t}$

حيث $d$ هي المسافة التي تقطعها الإشارة و $t$ هو الوقت المستغرق لقطع هذه المسافة. العلاقة الثانية تتعلق بعكس الوقت، التردد، للإشارة. العلاقة هنا

c = f λ

حيث $f$ هو تردد الإشارة و $λ$ هو طول الموجة . تستخدم القياسات التردد كمقياس لظاهرة الرنين الصوتي حيث $n$ يتطابق عدد أطوال الموجات مع الطول الذي تردد عليه الإشارة. تعتمد كلتا الطريقتين على المسافة التي تقيسها، إما بشكل مباشر كما في زمن الرحلة، أو بشكل غير مباشر من خلال عدد الأطوال الموجية المطابقة على المدى المادي للعينة التي يتردد صداها.

مثال على تقنيات الاختبار بالموجات فوق الصوتية

بشكل عام، هناك طريقتان لإنشاء نظام محول لقياس سرعة الصوت في مادة صلبة. أحدهما عبارة عن إعداد يحتوي على محولين أو أكثر حيث يعمل أحدهما كمرسل، بينما يعمل الآخر (ق) كجهاز استقبال. يمكن بعد ذلك قياس سرعة الصوت عن طريق قياس الوقت بين إشارة يتم إنشاؤها في جهاز الإرسال وعندما يتم تسجيلها في المستقبل مع افتراض معرفة (أو قياس) المسافة التي قطعتها الإشارة الصوتية بين المحولات، أو العكس قياس تردد الرنين مع معرفة السماكة التي يتردد صداها. غالبًا ما يُطلق على النوع الآخر من الإعداد نظام صدى النبض. هنا يتم وضع محول طاقة واحد بالقرب من العينة يعمل كمرسل ومستقبل. يتطلب ذلك واجهة عاكسة حيث يمكن أن تنعكس الإشارة المولدة مرة أخرى باتجاه محول الطاقة الذي يعمل بعد ذلك كمستقبل يسجل الإشارة المنعكسة. انظر اختبار الموجات فوق الصوتية لبعض أنظمة القياس.

موجات القص الطولية والمستقطبة

كما هو موضح أعلاه، هناك مجموعة من ثلاثة استقطابات متعامدة ( $m$ ) لحركة الجسيمات لاتجاه انتشار معين $N$ في صلب. بالنسبة لإعدادات القياس حيث يمكن تثبيت المحولات مباشرة على العينة قيد التحقيق، فمن الممكن إنشاء هذه الاستقطابات الثلاثة (موجتان طولية وموجات عرضية متعامدة) من خلال تطبيق أنواع مختلفة من محولات الطاقة التي تثير الاستقطاب المطلوب (على سبيل المثال، محولات كهرضغطية مع المطلوب وضع التذبذب ). وبالتالي، من الممكن قياس سرعة الصوت للموجات مع جميع الاستقطابات الثلاثة من خلال إعدادات قياس تعتمد على الوقت أو تعتمد على التردد اعتمادًا على اختيار أنواع محول الطاقة. ومع ذلك، إذا تعذر تثبيت محول الطاقة على عينة الاختبار، فسيلزم وجود وسيط اقتران لنقل الطاقة الصوتية من محول الطاقة إلى العينة. غالبًا ما يتم استخدام الماء أو المواد الهلامية كوسيلة اقتران. يعتبر هذا كافيًا لقياس سرعة الصوت الطولية، ولكن السوائل لا تحمل موجات القص، وبالتالي لتكون قادرًا على توليد وقياس سرعة موجات القص في عينة الاختبار، يجب أن تتفاعل الموجة الطولية الساقطة بزاوية مائلة عند السائل / سطح صلب لتوليد موجات القص من خلال تحويل الوضع . يتم بعد ذلك تحويل موجات القص هذه مرة أخرى إلى موجات طولية عند السطح الصلب / السائل الذي ينتشر مرة أخرى عبر السائل إلى محول طاقة التسجيل مما يتيح قياس سرعات موجات القص أيضًا من خلال وسيط اقتران.

التطبيقات

المواد الهندسية - تقدير الإجهاد

نظرًا لأن الصناعة تسعى جاهدة لتقليل تكاليف الصيانة والإصلاح، فإن الاختبار غير المدمر للهياكل يصبح ذا قيمة متزايدة في كل من التحكم في الإنتاج وكوسيلة لقياس استخدام وحالة البنية التحتية الرئيسية. هناك العديد من تقنيات القياس لقياس الضغط في مادة ما . ومع ذلك، فإن التقنيات التي تستخدم القياسات البصرية والقياسات المغناطيسية وانحراف الأشعة السينية والحيود النيوتروني كلها تقتصر على قياس الإجهاد السطحي أو بالقرب من السطح أو الإجهاد. تنتشر الموجات الصوتية بسهولة من خلال المواد وتوفر بالتالي وسيلة لاستكشاف الأجزاء الداخلية من الهياكل، حيث يكون مستوى الإجهاد والانفعال مهمين للسلامة الهيكلية الشاملة. نظرًا لأن سرعة الصوت لمثل هذه المواد المرنة غير الخطية (بما في ذلك مواد البناء الشائعة مثل الألومنيوم والصلب ) تعتمد على الإجهاد، فقد يكون أحد تطبيقات تأثير المرونة الصوتية هو قياس حالة الإجهاد في الجزء الداخلي من مادة محملة باستخدام مجسات صوتية مختلفة (مثل الاختبار بالموجات فوق الصوتية ) لقياس التغير في سرعات الصوت.

المواد الحبيبية والمسامية - الجيوفيزياء

يدرس علم الزلازل انتشار الموجات المرنة عبر الأرض ويستخدم على سبيل المثال في دراسات الزلازل وفي رسم خرائط باطن الأرض . يتعرض الجزء الداخلي من الأرض لضغوط مختلفة، وبالتالي قد تمر الإشارات الصوتية عبر الوسائط في حالات ضغط مختلفة. وبالتالي قد تكون نظرية المرونة الصوتية ذات أهمية عملية حيث يمكن استخدام سلوك الموجة غير الخطية لتقدير الخصائص الجيوفيزيائية.^[8]

الأنسجة الرخوة - الموجات فوق الصوتية الطبية

قد تكون التطبيقات الأخرى في التصوير فوق الصوتي الطبي والتصوير المرن لقياس الضغط أو مستوى الضغط في أنواع الأنسجة المرنة ذات الصلة (على سبيل المثال ^[19]^[20]^[21] )، مما يعزز التشخيص غير الجراحي.

انظر أيضًا

مراجع

^ ^أ ^ب ^ت ^ث ^ج ^ح Ogden, R. W., Non-linear elastic deformations, Dover Publications Inc., Mineola, New York, (1984)
^ Brillouin، Léon (1925). "Les tensions de radiation ; leur interprétation en mécanique classique et en relativité". Journal de Physique et le Radium. ج. 6 ع. 11: 337–353. DOI:10.1051/jphysrad:01925006011033700. ISSN:0368-3842.
^ Tang، Sam (1967). "Wave propagation in initially-stressed elastic solids". Acta Mechanica. ج. 4 ع. 1: 92–106. DOI:10.1007/BF01291091. ISSN:0001-5970.
^ ^أ ^ب ^ت Murnaghan، F. D. (1937). "Finite Deformations of an Elastic Solid". American Journal of Mathematics. ج. 59 ع. 2: 235–260. DOI:10.2307/2371405. ISSN:0002-9327. JSTOR:2371405.
^ Hughes، D. S.؛ Kelly، J. L. (1953). "Second-Order Elastic Deformation of Solids". Physical Review. ج. 92 ع. 5: 1145–1149. Bibcode:1953PhRv...92.1145H. DOI:10.1103/PhysRev.92.1145. ISSN:0031-899X.
^ "Anisotropy and Isotropy". مؤرشف من الأصل في 2012-05-31. اطلع عليه بتاريخ 2013-12-07.
^ ^أ ^ب ^ت Norris, A. N. (1997). "Finite-Amplitude Waves in Solids". في Hamilton، Mark F.؛ Blackstock، David T. (المحررون). Nonlinear Acoustics. Acoustical Society of America. ISBN:978-0123218605.
^ ^أ ^ب ^ت ^ث ^ج ^ح Norris, A. N. (2007). "Small-on-Large Theory with Applications to Granular Materials and Fluid/Solid Systems" (PDF). في M. Destrade؛ G. Saccomandi (المحررون). Waves in Nonlinear Pre-Stressed Materials. CISM Courses and Lectures. Springer, Vienna. ج. 495. DOI:10.1007/978-3-211-73572-5. ISBN:978-3-211-73572-5.
^ ^أ ^ب Eldevik, S., "Measurement of non-linear acoustoelastic effect in steel using acoustic resonance", PhD Thesis, University of Bergen, (in preparation)
^ ^أ ^ب ^ت ^ث ^ج Ogden, R. W. (2007). "Incremental Statics and Dynamics of Pre-Stressed Elastic Materials" (PDF). في M. Destrade؛ G. Saccomandi (المحررون). Waves in Nonlinear Pre-Stressed Materials. CISM Courses and Lectures. Springer, Vienna. ج. 495. DOI:10.1007/978-3-211-73572-5. ISBN:978-3-211-73572-5.
^ ^أ ^ب Landau, L. D.؛ Lifshitz, E. M. (1970). Theory of Elasticity (ط. second). Pergamon Press. ISBN:9780080064659. مؤرشف من الأصل في 2017-05-31.
^ Toupin، R. A.؛ Bernstein، B. (1961). "Sound Waves in Deformed Perfectly Elastic Materials. Acoustoelastic Effect". The Journal of the Acoustical Society of America. ج. 33 ع. 2: 216–225. Bibcode:1961ASAJ...33..216T. DOI:10.1121/1.1908623. ISSN:0001-4966.
^ Bland, D. R., Nonlinear dynamic elasticity, Blaisdell Waltham, (1969)
^ Suhubi, E. S., Eringen, A. C., Elastodynamics, Academic press New York, (1974)
^ ^أ ^ب ^ت ^ث ^ج Smith، R. T.؛ Stern، R.؛ Stephens، R. W. B. (1966). "Third‐Order Elastic Moduli of Polycrystalline Metals from Ultrasonic Velocity Measurements". The Journal of the Acoustical Society of America. ج. 40 ع. 5: 1002–1008. Bibcode:1966ASAJ...40.1002S. DOI:10.1121/1.1910179. ISSN:0001-4966.
^ Crecraft، D.I. (1967). "The measurement of applied and residual stresses in metals using ultrasonic waves". Journal of Sound and Vibration. ج. 5 ع. 1: 173–192. Bibcode:1967JSV.....5..173C. DOI:10.1016/0022-460X(67)90186-1. ISSN:0022-460X.
^ ^أ ^ب Egle، D. M.؛ Bray، D. E. (1976). "Measurement of acoustoelastic and third‐order elastic constants of rail steel". The Journal of the Acoustical Society of America. ج. 59 ع. S1: S32. Bibcode:1976ASAJ...59...32E. DOI:10.1121/1.2002636. ISSN:0001-4966.
^ Abiza، Z.؛ Destrade، M.؛ Ogden، R.W. (2012). "Large acoustoelastic effect". Wave Motion. ج. 49 ع. 2: 364–374. arXiv:1302.4555. DOI:10.1016/j.wavemoti.2011.12.002. ISSN:0165-2125.
^ Gennisson، J.-L.؛ Rénier، M.؛ Catheline، S.؛ Barrière، C.؛ Bercoff، J.؛ Tanter، M.؛ Fink، M. (2007). "Acoustoelasticity in soft solids: Assessment of the nonlinear shear modulus with the acoustic radiation force". The Journal of the Acoustical Society of America. ج. 122 ع. 6: 3211–3219. Bibcode:2007ASAJ..122.3211G. DOI:10.1121/1.2793605. ISSN:0001-4966. PMID:18247733.
^ Jun Wu؛ Wei He؛ Wei-min Chen؛ Lian Zhu (2013). "Research on simulation and experiment of noninvasive intracranial pressure monitoring based on acoustoelasticity effects". Medical Devices: Evidence and Research. ج. 6: 123–131. DOI:10.2147/MDER.S47725. PMID:24009433. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)
^ Duenwald، Sarah؛ Kobayashi، Hirohito؛ Frisch، Kayt؛ Lakes، Roderic؛ Vanderby، Ray (2011). "Ultrasound echo is related to stress and strain in tendon". Journal of Biomechanics. ج. 44 ع. 3: 424–429. DOI:10.1016/j.jbiomech.2010.09.033. ISSN:0021-9290. PMID:21030024. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)

بوابة علم المواد

[ogden-1] أ ^ب ^ت ^ث ^ج ^ح Ogden, R. W., Non-linear elastic deformations, Dover Publications Inc., Mineola, New York, (1984)

[Brillouin1925-2] Brillouin، Léon (1925). "Les tensions de radiation ; leur interprétation en mécanique classique et en relativité". Journal de Physique et le Radium. ج. 6 ع. 11: 337–353. DOI:10.1051/jphysrad:01925006011033700. ISSN:0368-3842.

[Tang1967-3] Tang، Sam (1967). "Wave propagation in initially-stressed elastic solids". Acta Mechanica. ج. 4 ع. 1: 92–106. DOI:10.1007/BF01291091. ISSN:0001-5970.

[Murnaghan-4] أ ^ب ^ت Murnaghan، F. D. (1937). "Finite Deformations of an Elastic Solid". American Journal of Mathematics. ج. 59 ع. 2: 235–260. DOI:10.2307/2371405. ISSN:0002-9327. JSTOR:2371405.

[HughesKelly1953-5] Hughes، D. S.؛ Kelly، J. L. (1953). "Second-Order Elastic Deformation of Solids". Physical Review. ج. 92 ع. 5: 1145–1149. Bibcode:1953PhRv...92.1145H. DOI:10.1103/PhysRev.92.1145. ISSN:0031-899X.

[6] "Anisotropy and Isotropy". مؤرشف من الأصل في 2012-05-31. اطلع عليه بتاريخ 2013-12-07.

[norris97-7] أ ^ب ^ت Norris, A. N. (1997). "Finite-Amplitude Waves in Solids". في Hamilton، Mark F.؛ Blackstock، David T. (المحررون). Nonlinear Acoustics. Acoustical Society of America. ISBN:978-0123218605.

[norris07-8] أ ^ب ^ت ^ث ^ج ^ح Norris, A. N. (2007). "Small-on-Large Theory with Applications to Granular Materials and Fluid/Solid Systems" (PDF). في M. Destrade؛ G. Saccomandi (المحررون). Waves in Nonlinear Pre-Stressed Materials. CISM Courses and Lectures. Springer, Vienna. ج. 495. DOI:10.1007/978-3-211-73572-5. ISBN:978-3-211-73572-5.

[eldevik-9] أ ^ب Eldevik, S., "Measurement of non-linear acoustoelastic effect in steel using acoustic resonance", PhD Thesis, University of Bergen, (in preparation)

[ogden07-10] أ ^ب ^ت ^ث ^ج Ogden, R. W. (2007). "Incremental Statics and Dynamics of Pre-Stressed Elastic Materials" (PDF). في M. Destrade؛ G. Saccomandi (المحررون). Waves in Nonlinear Pre-Stressed Materials. CISM Courses and Lectures. Springer, Vienna. ج. 495. DOI:10.1007/978-3-211-73572-5. ISBN:978-3-211-73572-5.

[LandauLifshitz-11] أ ^ب Landau, L. D.؛ Lifshitz, E. M. (1970). Theory of Elasticity (ط. second). Pergamon Press. ISBN:9780080064659. مؤرشف من الأصل في 2017-05-31.

[ToupinBernstein1961-12] Toupin، R. A.؛ Bernstein، B. (1961). "Sound Waves in Deformed Perfectly Elastic Materials. Acoustoelastic Effect". The Journal of the Acoustical Society of America. ج. 33 ع. 2: 216–225. Bibcode:1961ASAJ...33..216T. DOI:10.1121/1.1908623. ISSN:0001-4966.

[Bland-13] Bland, D. R., Nonlinear dynamic elasticity, Blaisdell Waltham, (1969)

[EringSuhubi-14] Suhubi, E. S., Eringen, A. C., Elastodynamics, Academic press New York, (1974)

[smith-15] أ ^ب ^ت ^ث ^ج Smith، R. T.؛ Stern، R.؛ Stephens، R. W. B. (1966). "Third‐Order Elastic Moduli of Polycrystalline Metals from Ultrasonic Velocity Measurements". The Journal of the Acoustical Society of America. ج. 40 ع. 5: 1002–1008. Bibcode:1966ASAJ...40.1002S. DOI:10.1121/1.1910179. ISSN:0001-4966.

[Crecraft1967-16] Crecraft، D.I. (1967). "The measurement of applied and residual stresses in metals using ultrasonic waves". Journal of Sound and Vibration. ج. 5 ع. 1: 173–192. Bibcode:1967JSV.....5..173C. DOI:10.1016/0022-460X(67)90186-1. ISSN:0022-460X.

[egle_bay-17] أ ^ب Egle، D. M.؛ Bray، D. E. (1976). "Measurement of acoustoelastic and third‐order elastic constants of rail steel". The Journal of the Acoustical Society of America. ج. 59 ع. S1: S32. Bibcode:1976ASAJ...59...32E. DOI:10.1121/1.2002636. ISSN:0001-4966.

[AbizaDestrade2012-18] Abiza، Z.؛ Destrade، M.؛ Ogden، R.W. (2012). "Large acoustoelastic effect". Wave Motion. ج. 49 ع. 2: 364–374. arXiv:1302.4555. DOI:10.1016/j.wavemoti.2011.12.002. ISSN:0165-2125.

[GennissonRénier2007-19] Gennisson، J.-L.؛ Rénier، M.؛ Catheline، S.؛ Barrière، C.؛ Bercoff، J.؛ Tanter، M.؛ Fink، M. (2007). "Acoustoelasticity in soft solids: Assessment of the nonlinear shear modulus with the acoustic radiation force". The Journal of the Acoustical Society of America. ج. 122 ع. 6: 3211–3219. Bibcode:2007ASAJ..122.3211G. DOI:10.1121/1.2793605. ISSN:0001-4966. PMID:18247733.

[20] Jun Wu؛ Wei He؛ Wei-min Chen؛ Lian Zhu (2013). "Research on simulation and experiment of noninvasive intracranial pressure monitoring based on acoustoelasticity effects". Medical Devices: Evidence and Research. ج. 6: 123–131. DOI:10.2147/MDER.S47725. PMID:24009433. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)

[DuenwaldKobayashi2011-21] Duenwald، Sarah؛ Kobayashi، Hirohito؛ Frisch، Kayt؛ Lakes، Roderic؛ Vanderby، Ray (2011). "Ultrasound echo is related to stress and strain in tendon". Journal of Biomechanics. ج. 44 ع. 3: 424–429. DOI:10.1016/j.jbiomech.2010.09.033. ISSN:0021-9290. PMID:21030024. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

[11]

[12]

[13]

[14]

[15]

[16]

[17]

[18]

[19]

[20]

[21]

تأثير صوتي مرن

محتويات

نظرية المرونة غير الخطية للمواد فائقة المرونة