مبرهنة بايز

في نظرية الاحتمالات والإحصاء، تصف مبرهنة بايز (التي تعرف أيضا بقانون بايز أو قاعدة بايز) احتمال وقوع حدث، بناءً على المعرفة المسبقة بالظروف التي قد تكون ذات صلة بالحدث. على سبيل المثال، إذا كان السرطان مرتبطًا بالتقدم في العمر، فعند استخدام مبرهنة بايز، يمكن استخدام عمر الشخص لإجراء تقييم لاحتمال إصابته بالسرطان أكثر دقة مما يمكن عمله دون معرفة عمر الشخص.

أحد التطبيقات العديدة لمبرهنة بايز هو الاستدلال البايزي وهي أحد طرق الاستدلال الإحصائي. عند تطبيق الاستدلال البايزي، قد يكون للاحتمالات التي تنطوي عليها مبرهنة بايز (Bayesian interpretation of probability) مدلول مختلف عن المفهوم التكراري للاحتمالات (Frequentist interpretation of probability). باستخدام التفسير البايزي للاحتمالات (Bayesian interpretation of probability)، فإن النظرية تبين إلى أي درجة يجب أن تتغير درجة اعتقادنا في أمر ما (وهو ما نعبر عنه على شكل احتمال حدوث هذا الأمر) بعد الأخذ في الاعتبار الأدلة الجديدة التي أصبحت متوفرة. لذلك فان الاستدلال البايزي يعد مفهوما أساسيا في الإحصاء البايزي.

سميت مبرهنة بايز على اسم القس توماس بايز (1701 - 1761)، الذي استخدم الاحتمال الشرطي لأول مرة لتوفير خوارزمية (في فرضيته رقم 9) الذي تستخدم القرائن (evidences) لحساب حدود متغير غير معروف،

هذه الخوارزمية نشرت تحت عنوان مقال نحو حل مشكلة في عقيدة الاحتمالات (عام 1763). فيما أسماه ب”تعليق” ، طور بايز خوارزميته لتشمل أي مسبب غير معروف.

استخدم العالم بيير لابلاس في عام 1774 (وبعد ذلك في بحثه بعنوان “نظرية الاحتمالات التحليلية” الذي نشرعام 1812) الاحتمال الشرطي لصياغة علاقة الاحتمال البعدي (أو اللاحق) المحدث بالاحتمال القبلي (أو المسبق) بعلومية الأدلة. ثم جاء بعد ذلك السير هارولد جيفريز ليضع كلا من خوارزمية بايز وصياغة لابلاس على أساس بديهي. كتب جيفريز أن أهمية مبرهنة بايز «لنظرية الاحتمالات هي كأهمية نظرية فيثاغورس للهندسة.»^[1]

برهان مبدئي لمبرهنة بايز

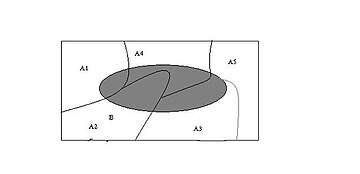
لنفرض أن الأحداث $A_{1}$ و $A_{2}$ و $A_{3}$ و $A_{4}$ و $A_{5}$ تشكل تجزيئا لفضاء العينة $S$ . أي أن $A_{1}$ و $A_{2}$ و $A_{3}$ و $A_{4}$ و $A_{5}$ مجموعات جزئية من فضاء العينة $S$ متنافية مثنى مثنى (لا يوجد تقاطع بين أي اثنين منها، واجتماعها جميعها يشكل فضاء العينة بكامله). لنفرض أن حدثا ضمن فضاء العينة $B$ (المنطقة المظللة) فإن:^[2]

B = (S \cap B) = (A_{1} \cap B) \cup (A_{2} \cap B) \cup (A_{3} \cap B) \cup (A_{4} \cap B) \cup (A_{5} \cap B)

وبما أن $A_{1}$ و $A_{2}$ و $A_{3}$ و $A_{4}$ و $A_{5}$ متنافية مثنى مثنى فإن الأحداث $B \cap A_{i}$ متنافية أيضا مثنى:

P (B) = P (A_{1} \cap B) + P (A_{2} \cap B) + P (A_{3} \cap B) + P (A_{4} \cap B) + P (A_{5} \cap B)

باستخدام علاقة الاحتمال الشرطي:

P (B) = P (B | A_{1}) P (A_{1}) + P (B | A_{2}) P (A_{2}) + P (B | A_{3}) P (A_{3}) + P (B | A_{4}) P (A_{4}) + P (B | A_{5}) P (A_{5})

مقولات مبرهنة بايز

تقوم مبرهنة بايز بربط الاحتمالات الشرطية conditional والاحتمالات الحافية marginal probabilities, لكي نقوم باستنتاج هذه المبرهنة، لا بد لنا أن نبدأ من تعريف الاحتمال الشرطي:^[3]

P (A | B) P (B) = P (A \cap B) = P (B | A) P (A)

وهو ما يقرأ (جداء الاحتمال الشرطي ل $A$ بمعرفة $B$ في احتمال $B$ ) يعطي احتمال حدوث $A$ و $B$ معا وهويساوي أيضا (جداء الاحتمال الشرطي ل $B$ بمعرفة $A$ في احتمال A).

باعتبار $P (B)$ ليس معدوما نقوم بقسمة طرفي المعادلة السابقة عليه:

P (A | B) = \frac{P (B | A) P (A)}{P (B)}

وهونص ما يعرف عادة بمبرهنة بايز.

تقرأ: " الاحتمال الشرطي للحدث $A$ بمعرفة الحدث $B$ يساوي إلى احتمال $B$ بمعرفة $A$ مضروبا باحتمال $A$ مقسوما على احتمال $B$ . "

انظر أيضا

المراجع

^ Harold (1973). Scientific inference. -. Cambridge [Eng.]: Cambridge University Press. مؤرشف من الأصل في 2020-02-13.
^ Stuart، A.؛ Ord، K. (1994)، Kendall's Advanced Theory of Statistics: Volume I—Distribution Theory، Edward Arnold، §8.7.
^ Daniel Kahneman (25 أكتوبر 2011). Thinking, Fast and Slow. Macmillan. ISBN:978-1-4299-6935-2. مؤرشف من الأصل في 2019-11-21. اطلع عليه بتاريخ 2012-04-08.

في كومنز صور وملفات عن: مبرهنة بايز

[1] Harold (1973). Scientific inference. -. Cambridge [Eng.]: Cambridge University Press. مؤرشف من الأصل في 2020-02-13.

[2] Stuart، A.؛ Ord، K. (1994)، Kendall's Advanced Theory of Statistics: Volume I—Distribution Theory، Edward Arnold، §8.7.

[Kahneman2011-3] Daniel Kahneman (25 أكتوبر 2011). Thinking, Fast and Slow. Macmillan. ISBN:978-1-4299-6935-2. مؤرشف من الأصل في 2019-11-21. اطلع عليه بتاريخ 2012-04-08.

[1]

[2]

[3]

مبرهنة بايز

محتويات

برهان مبدئي لمبرهنة بايز

مقولات مبرهنة بايز

انظر أيضا

المراجع

قائمة التصفح