حسابيات معيارية

الصفحة الأولى من الطبعة الأصلية من كتاب كارل فريدريش غاوس، **استفسارات حسابية**، الكتاب المؤسس للحسابيات النمطية.

في الرياضيات وبالتحديد في مجال النظرية الجبرية للأعداد، الحسابيات النمطية (بالإنجليزية: modular arithmetics)‏ هي مجموعة من الطرق التي تتيح حل بعض المسائل الخاصة بالأعداد الصحيحة و من ضمنها الطبيعية. وهي ترتكز على دراسة الباقي الحاصل من القسمة الإقليدية.

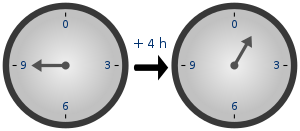
ترتكز الحسابيات النمطية أساسا على النظر إلى باقي قسمة الأعداد الطبيعية على عدد طبيعي معين ثابت ما، بدلا من النظر إلى هذه الأعداد ذاتها. يظهر هذا جليا في مثال حسابيات المنبه، الذي يوافق حالة n=12 : العقرب الصغير يوجد في نفس الموضع في لحظتين تفصل بينهما اثنتا عشرة ساعة، وبهذا تصير الساعة 1 كالساعة 13.

استعمالات

في الرياضيات الأساسية, هذا المفهوم قليل الاستعمال. التوظيف الأكثر استعمالا هو المبرهنة الجيرية للأعداد,^[1] التي تتضمن مجالا أكثر توسعا, تتضمن مثلا مفاهيم الأعداد الجبرية ومبرهنة غالوا.^[2]

في الرياضيات التطبيقية, لهذه العبارة استعمالات مكثفة في أساسيات الرياضيات في مختلف مجالات نظرية المعلوميات كالتشفير ونظرية الترميز والمعلوميات. لعدد من الأدوات وخوارزميات داخل هذا المجال نجد اختبار أولية عدد ما والتفكيك إلى جداء عوامل أولية,^[3] استعمال مميزات مجموعة مثلا بالنسبة لتحويل فوريي المتقطع^[4] أو دراسة الخارج أو الخاصة بالأعداد الطبيعية, كما في الدوال الحدودية.^[5]

حسب مختلف العلماء والمألفين وحسب مجال التطبيق, تعتبر هذه التمديدات, إما جزء من الحسابيات النمطية^[6] أو تطبيقات أو غير مصنفة. في صيغتها البسيطة, تحمل في بعض الأحيان حسابيات المنبه.^[7] المفهوم نظام نمطي مستعمل^[8] في الحسابيات النمطية في مجموعات أعداد غير الأعداد الطبيعية.

التاريخ

الأصول الأولى

الصفحة الأولى لطبعة 1621 ل أريثميتيكا (كتاب) لمؤلفه ديوفانتوس الإسكندري، المترجمة إلى اللاتينية من طرف كلود غاسبارد باشي دي ميزيرياك.

الظهور في أوروبا

بيير دي فيرما développe largement l'حسابيات. Les propriétés de la خوارزمية تقسيم, fondement de l'arithmétique modulaire, sont largement utilisées par ce mathématicien.

الطرق المستعملة

مساهمات كارل فريدريش غاوس

القرن العشرون

التعمية

*آلة إنجما*, آلة للتعمية استعملت خلال الحرب العالمية الثانية، كُسر تشفيرها من طرف عالم الرياضيات ماريان رييفسكي.

نظرية المعلومات

وسائل الحسابيات النمطية

تساوي عددين بتردد عدد ثالث

للحصول على حساب من نوع هذه المجموعة, علينا التأكد من كون عمليـّـتي الجمع والضرب متكافئة مع تعريفهما.

بالنسبة لكارل فريدرش غاوس فقد أضاف تحليل بنية هذه المجموعة, والمسماة حلقة ل تقارب ورمزها Z/nZ. تهتم أولا بدراسة عملية الجمع, الذي يعرف بزمرة دائرية ذات المولد 1 ; ثم عملية الضرب, المستقل عن خصائص التطابق (congruency) . إذا كان هذا عددا أوليا, نحصل على حقل . هذه المقاربة تسهل عملية المبرهنة في مجال الحسابيات. المثالان التاريخيان من كتاب Disquisitiones arithmeticae تبع الرياضياتي الألماني غاوس هما مبرهنة ويلسون^[9] والبرهنة على مبرهنة فيرما الصغرى.^[10]

الحسابيات النمطية ، في حالة لم يكن الترديد عددا أوليا ، أكثر تعقيدا. مبرهنة الباقي الصيني تسمح بتنوير البنية. الحلقة غير داخلية, حيث يوجد قواسم الصفر, وهي أعداد إذا ضربت في أعداد غير منعدمة أعطت كنتيجة العدد صفر. عدد العناصر المقلوبة معطاة بواسطة مؤشر أويلر. وهي تتيح مثلا, تعميم مبرهنة فيرما الصغرى.

الأعداد الصحيحة الجبرية

حروف دركليه

طور يوهان بيتر غوستاف لوجون دركليه الجزء الأساسي من النظرية في إطار الحلقة ℤ/nℤ.

درس دركليه الأعداد الأولية اللائي يأخذن الشكل n + λm حيث m و n عددان أوليان فيما بينهما وحيث λ عدد طبيعي ما. فحاول البرهان على أن هناك عددا غير منتهي من هذه الأعداد الأولية.

أساسيات

تعتبر الحسابيات النمطية نظاما حسابيا للأعداد الصحيحة يعتمد على تكرار الأعداد بشكل نمطي لدى بلوغها قيمة نمطية معينة ، و هي تـُـخـْـتـَـزَل بالتعبير $(\mod)$ . مرتبط بذلك الرياضياتيون يتكلمون عن «تطابق» (congruency) .

على فرض لدينا عدد صحيح موجب $n$ وعدد صحيح $a$ فإننا بقسمة $a$ على $n$ نحصل على عدد صحيح $q$ هو ناتج القسمة وعدد صحيح $r$ هو باقي القسمة بحيث يحققان العلاقة التالية:

$a = q n + r 0 \leq r < n; q = ⌊ \frac{a}{n} ⌋$

حيث الصيغة $⌊ x ⌋$ تعني أكبر عدد صحيح أصغر أو يساوي $x$

يرمز إلى عملية حساب باقي القسمة ب mod حيث نكتب $r = a mod n$ وبالتالي:

$a = ⌊ \frac{a}{n} ⌋ \times n + (a mod n)$

أمثلة:

$5 mod 7 = 5$

$0 mod 7 = 0$

$7 mod 7 = 0$

$11 mod 7 = 4$

$- 11 mod 7 = 3$

نقول عن عددين صحيحين $a$ و $b$ بانهما متوافقان بقياس $n$ إذا تحقق $(a mod n) = (b mod n)$ ونرمز لذلك بـ $a \equiv b mod n$

خصائص عملية حساب باقي القسمة

$a \equiv b mod n$ إذا و إذا كان فقط $n ∣ (a - b)$
$a \equiv b mod n ⟺ b \equiv a mod n$
$a \equiv b mod n \land b \equiv c mod n ⟹ a \equiv c mod n$

خصائص الحسابيات النمطية

$(x y) mod m = ((x mod m) (y mod m)) mod m$

$(x + y) mod m = ((x mod m) + (y mod m)) mod m$

$x^{n} mod m = ((x^{⌊ \frac{n}{2} ⌋} mod m) (x^{⌈ \frac{n}{2} ⌉} mod m)) mod m$

انظر أيضا

حقل منته
- مبرهنة الباقي الصيني
نظرية الأعداد
- زمرة دائرية
- مبرهنة أويلر
- مبرهنة فيرما الصغرى، حالة خاصة من مبرهنة أويلر
- مبرهنة لاغرانج (نظرية الزمر)

مراجع

^ قالب:Samuel1
^ A. Fröhlich, Galois Module structure of Algebraic integers, Springer-Verlag, Berlin, 1983.
^ Chantal David Cryptographie à clé publique et factorisation Université Concordia Quebec pp. 11-17 نسخة محفوظة 08 أكتوبر 2006 على موقع واي باك مشين. ^{[وصلة مكسورة]}
^ J-M Muller J-C Bajard Calcul arithmétique des ordinateurs Traité Hermes CNRS 2004 lire pp. 142-150 et pp. 181-201 نسخة محفوظة 09 أغسطس 2017 على موقع واي باك مشين.
^ Pascal Giorgi Arithmétique modulaire entière en base polynomiale Séminaire de l'université de Perpignan 2005 lire نسخة محفوظة 26 سبتمبر 2007 على موقع واي باك مشين. ^{[وصلة مكسورة]}
^ Thomas Plantard L'arithmétique modulaire pour la cryptographie Université de Montpelier 2005 lire نسخة محفوظة 05 نوفمبر 2012 على موقع واي باك مشين. ^{[وصلة مكسورة]}
^ سيمون لينا سينغ Histoire des codes secrets p. 324-329
^ Pascal Paillier Low-cost double-size modular exponentiation or how to stretch your cryptoprocessor GEMPLUS, ENST Lecture notes in computer science Springer, Berlin 1973
^ كارل فريدرش غاوس, Carl Friedrich Gauß: Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Ed. Courcier p56 1807
^ كارل فريدرش غاوس, Carl Friedrich Gauß: Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Ed. Courcier p. 34 1807

حسابيات معيارية في المشاريع الشقيقة:

[1] قالب:Samuel1

[2] A. Fröhlich, Galois Module structure of Algebraic integers, Springer-Verlag, Berlin, 1983.

[3] Chantal David Cryptographie à clé publique et factorisation Université Concordia Quebec pp. 11-17 نسخة محفوظة 08 أكتوبر 2006 على موقع واي باك مشين. ^{[وصلة مكسورة]}

[4] J-M Muller J-C Bajard Calcul arithmétique des ordinateurs Traité Hermes CNRS 2004 lire pp. 142-150 et pp. 181-201 نسخة محفوظة 09 أغسطس 2017 على موقع واي باك مشين.

[5] Pascal Giorgi Arithmétique modulaire entière en base polynomiale Séminaire de l'université de Perpignan 2005 lire نسخة محفوظة 26 سبتمبر 2007 على موقع واي باك مشين. ^{[وصلة مكسورة]}

[6] Thomas Plantard L'arithmétique modulaire pour la cryptographie Université de Montpelier 2005 lire نسخة محفوظة 05 نوفمبر 2012 على موقع واي باك مشين. ^{[وصلة مكسورة]}

[7] سيمون لينا سينغ Histoire des codes secrets p. 324-329

[8] Pascal Paillier Low-cost double-size modular exponentiation or how to stretch your cryptoprocessor GEMPLUS, ENST Lecture notes in computer science Springer, Berlin 1973

[9] كارل فريدرش غاوس, Carl Friedrich Gauß: Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Ed. Courcier p56 1807

[10] كارل فريدرش غاوس, Carl Friedrich Gauß: Recherches arithmétiques, 1801 Traduction M. Poullet-Delisle Ed. Courcier p. 34 1807

[1]

[2]

[3]

[4]

[5]

[6]

[7]

[8]

[9]

[10]

وصلة مكسورة

حسابيات معيارية

محتويات

استعمالات