|
تضامنًا مع حق الشعب الفلسطيني |
حدسية كولاتز
حدسية كولاتز |


حدسية كولاتز (بالإنجليزية: Collatz conjecture) هي حدسية في الرياضيات سميت هكذا نسبة إلى لوثار كولاتز, حدسها عام 1937.[1] قد تسمى أيضا حدسية 3n + 1[2] و حدسية أولام (نسبة إلى العالم البولندي ستانيسلو أولام) و معضلة كاكوتاني (نسبة إلى شيزوو كاكوتاني) و حدسية توايتس (نسبة إلي سير برايان توايتس) وخوارزمية هاس (نسبة إلى هيلموت هاس) ومعضلة سيراكوز.
قال بول إيردوس عن هذه الحدسية : الرياضيات ليست ناضجة بما فيه الكفاية لكي تحل معضلة كهذه، كما منح جائزة خمسمائة دولار أمريكي لمن يحلها.
في عام 2007، أُثبت أن أي تعميم طبيعي لمعضلة كولاتز هو معضلة غير قابلة للقرار من الوجهة الخوارزمية.
نص المعضلة
حدسية كولاتز خاصة بالأعداد الصحيحة الطبيعية غير المعدومة، وهي عبارة عن متتالية كما يلي:
- إذا كان العدد زوجيا، نقسمه على 2.
- إذا كان العدد فرديا، نضربه في 3 ونضيف له 1.
باستعمال رموز الحسابيات النمطية, لتكن الدالة f معرفة كما يلي:
إذا كررنا العملية عدة مرات، سنصل دائما ل 1، مهما كان عدد الانطلاق، وهذه هي الحدسية التي لم تثبت صحتها أو خطأها.
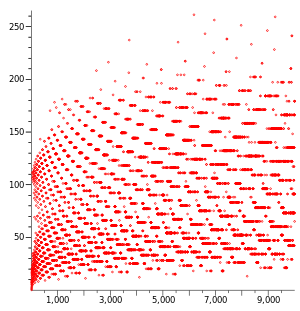
أمثلة
إذا كانت قيمة العدد الأول هو 6، فسيُحصل على المتتالية 6، 3، 10، 5، 16، 8، 4، 2، 1.
11 على سبيل المثال، المتتالية تمر على عدد أكبر من الحدود لكي تصل إلى الواحد: 11، 34، 17، 52، 26، 13، 40، 20، 10، 5، 16، 8، 4، 2، 1.
بالنسبة ل n = 27، تصل المتتالية إلى الواحد بعد 111 خطوة، صاعدة إلى 9232 قبل أن تنزل إلى الواحد. فيما يلي لائحة حدودها وبيان يمثلها:
- { 27, 82, 41, 124, 62, 31, 94, 47, 142, 71, 214, 107, 322, 161, 484, 242, 121, 364, 182, 91, 274, 137, 412, 206, 103, 310, 155, 466, 233, 700, 350, 175, 526, 263, 790, 395, 1186, 593, 1780, 890, 445, 1336, 668, 334, 167, 502, 251, 754, 377, 1132, 566, 283, 850, 425, 1276, 638, 319, 958, 479, 1438, 719, 2158, 1079, 3238, 1619, 4858, 2429, 7288, 3644, 1822, 911, 2734, 1367, 4102, 2051, 6154, 3077, 9232, 4616, 2308, 1154, 577, 1732, 866, 433, 1300, 650, 325, 976, 488, 244, 122, 61, 184, 92, 46, 23, 70, 35, 106, 53, 160, 80, 40, 20, 10, 5, 16, 8, 4, 2, 1 }

قوى العدد اثنين تعود إلى الواحد بسرعة لأن تُقسم على اثنين مرة لكي تعود إلى الواحد ولا تكبر قيمتها نهائيا.
صيغ أخرى للحدسية
بصفة عكسية

باعتبار آلة حاسبة مجردة تعمل في النظام الثنائي
مثال
111
1111
10110
10111
100010
100011
110100
11011
101000
1011
10000
تمديدات إلى مجالات أوسع
التكرار على الأعداد الصحيحة
التكرار على الأعداد الحقيقية أو العقدية

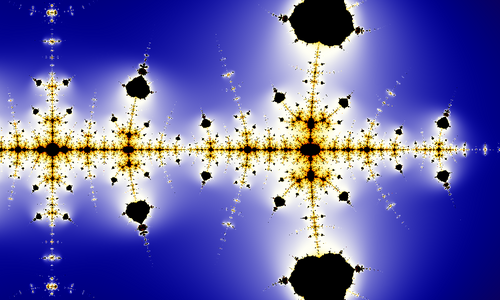
كسيرية كولاتز
مراجع
- ^ "معلومات عن حدسية كولاتز على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2019-06-16.
- ^ Alabbasi, Ahmad F (2023). "Mathematical analysis and proof of Collatz's conjecture" (بEnglish). DOI:10.13140/RG.2.2.34625.74087/1.
{{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب|دورية محكمة=(help)
انظر أيضا
| في كومنز صور وملفات عن: حدسية كولاتز |