اقتصاد مالي

من أرابيكا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث
  لمعانٍ أخرى، طالع اقتصاد مالي (توضيح).
اقتصاد مالي

تعديل - تعديل مصدريحول القالب

جزء من سلسلة مقالات حول
اقتصاد
  • تاريخ
  • أفرع
  • المفاهيم
  • النظرية
  • التقنيات
تطبيقات
اقتصاديون مميزون

الاقتصاد المالي هو فرع الاقتصاد الذي يتميز بـ «التركيز على الأنشطة النقدية»، والذي من المحتمل أن يظهر فيه «المال من نوع أو آخر على جانبي التجارة».[1] وبالتالي، فإن اهتمامها هو الترابط بين المتغيرات المالية، مثل الأسعار وأسعار الفائدة والأسهم، مقابل تلك المتعلقة بالاقتصاد الحقيقي. له مجالان رئيسيان للتركيز:[2] تسعير الأصول وتمويل الشركات؛ الأول هو منظور مقدمي رأس المال، أي المستثمرين، والثاني لمستخدمي رأس المال.

يتعلق الموضوع بـ «تخصيص ونشر الموارد الاقتصادية، مكانيا وعبر الزمن، في بيئة غير مستقرة».[3] لذلك فهو يركز على اتخاذ القرارات في ظل عدم اليقين في سياق الأسواق المالية، والنماذج والمبادئ الاقتصادية والمالية الناتجة، ويهتم باستنباط الآثار القابلة للاختبار أو السياسة من الافتراضات المقبولة. إنه مبني على أسس الاقتصاد الجزئي ونظرية القرار.

الاقتصاد القياسي هو فرع الاقتصاد المالي الذي يستخدم تقنيات الاقتصاد القياسي لتحديد معالم هذه العلاقات. يرتبط التمويل الرياضي بأنه سيشتق ويوسع النماذج الرياضية أو العددية المقترحة من قبل الاقتصاد المالي. لاحظ على الرغم من أن التركيز هناك هو الاتساق الرياضي، على عكس التوافق مع النظرية الاقتصادية. يركز الاقتصاد المالي في المقام الأول على الاقتصاد الجزئي، في حين أن الاقتصاد النقدي هو في المقام الأول الاقتصاد الكلي بطبيعته.

يتم تدريس الاقتصاد المالي عادة على مستوى الدراسات العليا؛ انظر ماجستير في الاقتصاد المالي. في الآونة الأخيرة، يتم تقديم شهادات جامعية متخصصة في التخصص.[4]

توفر هذه المقالة نظرة عامة واستطلاعًا حول الحقل: للحصول على مزيد من الاشتقاقات ومناقشة فنية أكثر، راجع المقالات المحددة المرتبطة.

الاقتصاد الأساسي

رموز تصنيف JEL
في رموز تصنيف مجلة الأدب الاقتصادي، يعد الاقتصاد المالي واحدًا من التصنيفات الـ 19 الأولية، في JEL: G. ويتبع الاقتصاد النقدي والدولي ويسبق الاقتصاد العام. للاطلاع على التصنيفات الفرعية التفصيلية، انظر أكواد تصنيف JEL الاقتصاد المالي.

يستخدم قاموس الجرافيك الجديد للاقتصاد (2008، الطبعة الثانية) أيضًا رموز JEL لتصنيف إدخالاته في الإصدار 8، فهرس الموضوع، بما في ذلك الاقتصاد المالي في صفحة.   863-64. فيما يلي روابط لملخصات إدخال The New Palgrave Online لكل فئة من فئات JEL الأساسية أو الثانوية (10 أو أقل لكل صفحة، على غرار عمليات بحث Google):

JEL: G - الاقتصاد المالي
JEL: G0 - عام
JEL: G1 - الأسواق المالية العامة
JEL: G2 - المؤسسات والخدمات المالية
JEL: G3 - تمويل الشركات والحوكمة

ويمكن أيضا إدخالات الفئة الثالثة يمكن البحث.[5]

كما ذكر أعلاه، يستكشف الانضباط بشكل أساسي كيف يمكن للمستثمرين العقلانيين تطبيق نظرية القرار على مشكلة الاستثمار. وبالتالي فإن الموضوع مبني على أسس الاقتصاد الجزئي ونظرية القرار، ويستخلص العديد من النتائج الرئيسية لتطبيق صنع القرار في ظل عدم اليقين في الأسواق المالية.

القيمة الحالية والتوقع والفائدة

تكمن وراء كل الاقتصاد المالي مفاهيم القيمة الحالية والتوقع.[6]

يسمح حساب القيمة الحالية لصانع القرار بتجميع التدفقات النقدية (أو العوائد الأخرى) التي يتم إنتاجها بواسطة الأصل في المستقبل، إلى قيمة واحدة في التاريخ المعني، وبالتالي مقارنة فرصتين بسهولة أكبر؛ وبالتالي هذا المفهوم هو نقطة الانطلاق لاتخاذ القرارات المالية. (تاريخها مبكرًا: يناقش ريتشارد ويت الاهتمام المركب بعمق بالفعل في عام 1613، في كتابه «أسئلة الحساب»؛ [7] بتطويره يوهان دي ويت وإدموند هالي.)

يتمثل الامتداد الفوري في الجمع بين الاحتمالات والقيمة الحالية، مما يؤدي إلى معيار القيمة المتوقعة الذي يحدد قيمة الأصول كدالة لأحجام الدفعات المتوقعة واحتمالات حدوثها. (هذه الأفكار تنبع من بليز باسكال وبيير دي فيرمات.)

ومع ذلك، تفشل طريقة القرار هذه في النظر في كره المخاطرة («كما يعرف أي طالب مالي» [6]). بمعنى آخر، نظرًا لأن الأفراد يحصلون على فائدة أكبر من دولار إضافي عندما يكونون فقراء وأقل فائدة عندما يكونون أغنياء نسبياً، فإن الطريقة هي «ضبط» الوزن المعين لمختلف النتائج («الحالات») في المقابل. (قد يكون بعض المستثمرين في الواقع يبحثون عن المخاطرة بدلاً من تجنب المخاطرة، ولكن نفس المنطق سينطبق).

قد يتم وصف الاختيار تحت عدم اليقين هنا بأنه تعظيم الفائدة المتوقعة. أكثر رسميا، مما أدى إلى فرضية فائدة المتوقع تنص على أنه، إذا راضون بعض البديهيات، وذاتية القيمة المرتبطة مقامرة من قبل فرد هو أن ' التوقع الإحصائي لتقييم نتائج تلك المقامرة.

ينشأ الدافع وراء هذه الأفكار من التناقضات المختلفة التي لوحظت في إطار القيمة المتوقعة، مثل مفارقة سان بطرسبرغ؛ انظر أيضا مفارقة إلسبرغ. (التطوير هنا يرجع أصلاً إلى دانييل بيرنولي، وتم إضفاء طابع رسمي عليه لاحقًا بواسطة جون فون نيومان وأوسكار مورغنسترن)

التسعير وخالية من التحكيم

ثم تقترن مفاهيم التحكيم- الحر، «العقلاني»، التسعير والتوازن مع ما سبق لاستخلاص الاقتصاد المالي «الكلاسيكي» [8] (أو «الكلاسيكي الجديد» [9]).

التسعير العقلاني هو افتراض أن أسعار الأصول (وبالتالي نماذج تسعير الأصول) ستعكس السعر الخالي من المراجحة للأصل، حيث إن «أي انحراف عن هذا السعر» سيتم «تحريفه». هذا الافتراض مفيد في تسعير الأوراق المالية ذات الدخل الثابت، وخاصة السندات، وهو أساسي لتسعير الأدوات المشتقة.

التوازن الاقتصادي هو، بوجه عام، حالة تتوازن فيها القوى الاقتصادية مثل العرض والطلب، وفي غياب التأثيرات الخارجية، لن تتغير قيم التوازن للمتغيرات الاقتصادية. يتعامل التوازن العام مع سلوك العرض والطلب والأسعار في الاقتصاد ككل مع العديد من الأسواق المتفاعلة أو العديد منها، من خلال السعي لإثبات وجود مجموعة من الأسعار ستؤدي إلى توازن شامل. (هذا على عكس التوازن الجزئي، الذي يحلل فقط الأسواق الموحدة.)

يرتبط المفهومان على النحو التالي: حيث لا تسمح أسعار السوق بمراجحة مربحة، أي أنها تشتمل على سوق خالية من المراجحة، ثم يقال إن هذه الأسعار تشكل «توازن موازنة». حدسيًا، يمكن ملاحظة ذلك من خلال التفكير في أنه في حالة وجود فرصة تحكيم، فمن المتوقع أن تتغير الأسعار، وبالتالي ليست في حالة توازن.[10] وبالتالي فإن موازنة التحكيم شرط مسبق لتحقيق التوازن الاقتصادي العام.

على الفور، وغير الرسمية، وتوسيع هذه الفكرة والنظرية الأساسية في تسعير الأصول، ويظهر أنه عندما تكون الأسواق كما -و صفه هي بالإضافة إلى ذلك (ضمنا وتبعا لذلك) كاملة قد -one ثم اتخاذ القرارات المالية عن طريق بناء مقياس المخاطر محايد احتمال المقابلة إلى السوق.

«اكتمال» هنا يعني أن هناك ثمنًا لكل أصل في كل حالة ممكنة من العالم، وبالتالي يمكن بناء المجموعة الكاملة من الرهانات المحتملة على دول العالم المستقبلية بأصول موجودة (مع عدم الاحتكاك) أساسا حل في وقت واحد لن الاحتمالات (خالية من المخاطر)، نظرا لارتفاع أسعار ن. سوف يشتق الاشتقاق الرسمي بحجج التحكيم.[6][10] للاطلاع على مثال عملي ، انظر التسعير الرشيد # التقييم المحايد للمخاطر، حيث يوجد في بيئة مبسطة، يوجد حالتان محتملتان فقط - للأعلى والأسفل - وحيث p و (1− p) هما الاحتمالان المقابلان (أي ضمني) وبدوره، التوزيع المشتق، أو "التدبير".

مع وجود هذا الإجراء في مكانه، فإن عائد أي ورقة مالية (أو محفظة) المتوقعة، أي ما هو مطلوب، سوف يساوي بعد ذلك العائد الذي لا ينطوي على مخاطر، بالإضافة إلى «تسوية للمخاطر»، [6] أي علاوة المخاطر الخاصة بالأمان، وتعويض المدى التي لا يمكن التنبؤ بتدفقاتها النقدية. جميع نماذج التسعير هي متغيرات أساسية لذلك، مع إعطاء افتراضات و/ أو شروط محددة.[6][11] يتماشى هذا النهج مع ما ورد أعلاه، ولكن مع التوقع القائم على «السوق» (أي خالي من المراجحة، ووفقًا للنظرية، وبالتالي في حالة توازن) بدلاً من التفضيلات الفردية.

وبالتالي، مع الاستمرار في المثال، لتقييم قيمة ورقة مالية معينة، يتم ضرب التدفقات النقدية المتوقعة في الدول الصاعدة والهابطة من خلال p و (1- p) على التوالي، ثم يتم خصمها بسعر فائدة خالي من المخاطر بالإضافة إلى متميزة. بشكل عام، قد يتم اشتقاق هذه العلاوة بواسطة C A P M (أو الامتدادات) كما سيظهر تحت # اليقين.

أسعار الدولة

مع إقامة العلاقة أعلاه، يمكن اشتقاق نموذج Arrow-D e b r e u المتخصص. تشير هذه النتيجة المهمة إلى أنه في ظل ظروف اقتصادية معينة، يجب أن يكون هناك مجموعة من الأسعار بحيث يكون إجمالي الإمدادات مساوياً للطلب الكلي على كل سلعة في الاقتصاد. غالبًا ما يتم إجراء التحليل هنا بافتراض وجود وكيل تمثيلي.[12]

ينطبق نموذج Arrow-D e b r e u على الاقتصادات التي تتمتع بأسواق كاملة إلى أقصى حد، حيث يوجد سوق لكل فترة زمنية وأسعار آجلة لكل سلعة في جميع الفترات الزمنية. الامتداد المباشر، إذن، هو مفهوم ضمان أسعار الدولة (يُطلق عليه أيضًا اسم أمان السهم - D e b r e u)، وهو عقد يوافق على دفع وحدة واحدة من n u m e r a i r e (عملة أو سلعة) في حالة حدوث حالة معينة ("up") "و" لأسفل "في المثال المبسط أعلاه) في وقت معين في المستقبل وتدفع قيمة الصفر في جميع الولايات الأخرى. ثمن هذا الأمن هو سعر الدولة لهذه الحالة بالذات في العالم.

في المثال أعلاه، فإن أسعار الدولة تعادل القيم الحالية التي تبلغ $ p و$ (1 − p): أي ما الذي سيدفعه اليوم، على التوالي، للأوراق المالية ذات الحالة العليا والدنيا؛ ناقل سعر الحالة هو ناقل أسعار الحالة لجميع الولايات. بالتطبيق على التقييم، سيكون سعر المشتق اليوم هو ببساطة السعر الأعلى × المردود المدفوع من الدولة + السعر المقلوب من الدولة × المردود المسقط؛ انظر أدناه فيما يتعلق بعدم وجود أي علاوة المخاطرة هنا. بالنسبة للمتغير العشوائي المستمر الذي يشير إلى استمرارية الحالات المحتملة، يتم العثور على القيمة من خلال التكامل على كثافة أسعار الولاية؛ انظر عامل الخصم العشوائي. يتم توسيع هذه المفاهيم لتشمل التسعير مارتينجال والتدبير محايد للمخاطر ذات الصلة.

تجد أسعار الولاية تطبيقًا فوريًا كأداة مفاهيمية («تحليل المطالبات الطارئة»)؛ [6] ولكن يمكن تطبيقها أيضًا على مشكلات التقييم.[13] بالنظر إلى آلية التسعير الموصوفة، يمكن للمرء تحليل القيمة المشتقة - في الواقع لكل «ورقة مالية» [2] - كتركيبة خطية من أسعارها الحكومية؛ أي حل الظهر للأسعار الدولة المقابلة لأسعار مشتقة لوحظ.[13][14] يمكن بعد ذلك استخدام أسعار الحالة المستردة لتقييم الأدوات الأخرى ذات التعرض الأقل من اللازم، أو لاتخاذ القرارات الأخرى المتعلقة بأقل من اللازم. (عمل B r e e d e n وL i t z e n b e r g e r في عام 1978 [15] أنشأ استخدام أسعار الدولة في الاقتصاد المالي.)

النماذج الناتجة

Modigliani-Miller Proposition II بدين محفوف بالمخاطر. مع زيادة الرافعة المالية (D / E)، يظل W A C C (k 0) ثابتًا.
كفاءة الحواف. يشار أحيانًا إلى "القطع الزائد" باسم "M a r k o w i t z Bullet" ، وجزءه المنحدر الصاعد هو الحدود الفعالة إذا لم تتوفر أصول خالية من المخاطر. مع الأصول الخالية من المخاطر ، فإن الخط الثابت هو الحدود الفعالة. يعرض الرسم CAL ، خط تخصيص رأس المال ، الذي يتكون عندما يكون الأصل الخطير أصل واحد وليس السوق، وفي هذه الحالة يكون الخط هو C M L.
خط سوق رأس المال هو خط الظل المرسوم من نقطة الأصل الخالي من المخاطر إلى المنطقة الممكنة للأصول الخطرة. تمثل نقطة الظل M حافظة السوق. ينتج C M L عن مزيج من محفظة السوق والأصول الخالية من المخاطر (النقطة L). تؤدي إضافة الرافعة المالية (النقطة R) إلى إنشاء حافظات ذات رافعة موجودة أيضًا في C M L.
حركات البني البراقة الهندسية مع معلمات من بيانات السوق.

بتطبيق المفاهيم الاقتصادية أعلاه، قد نستنتج بعد ذلك مختلف النماذج والمبادئ الاقتصادية والمالية. كما ذكر أعلاه، فإن مجالي التركيز المعتادين هما تسعير الأصول وتمويل الشركات، الأول هو منظور مقدمي رأس المال، والثاني لمستخدمي رأس المال. هنا، ولجميع نماذج الاقتصاد المالي (تقريبًا)، تكون الأسئلة التي يتم تناولها مؤطرة عادةً من حيث «الوقت، وعدم اليقين، والخيارات، والمعلومات»، [1][12] كما سنرى أدناه.

الوقت: يتم تداول المال الآن مقابل المال في المستقبل. عدم اليقين (أو المخاطرة): مبلغ المال الذي سيتم تحويله في المستقبل غير مؤكد.

الخيارات: يمكن لطرف واحد في المعاملة اتخاذ قرار في وقت لاحق يؤثر على التحويلات المالية اللاحقة. المعلومات: يمكن للمعرفة بالمستقبل أن تقلل أو ربما تقضي على عدم اليقين المرتبط بالقيمة النقدية المستقبلية (FMV).

تطبيق هذا الإطار، مع المفاهيم المذكورة أعلاه، يؤدي إلى النماذج المطلوبة. يبدأ هذا الاشتقاق بافتراض «عدم اليقين» ثم يتم توسيعه ليشمل الاعتبارات الأخرى. (يشير هذا القسمة في بعض الأحيان إلى «الحتمية» و«العشوائية»، [16] أو «العشوائية».)

السياقات

نقطة الانطلاق هنا هي «الاستثمار تحت اليقين». تؤكد نظرية فصل فيشر أن هدف الشركة هو زيادة قيمتها الحالية إلى الحد الأقصى، بغض النظر عن تفضيلات مساهميها. ذات الصلة هي نظرية Modigliani-Miller ، التي توضح أنه في ظل ظروف معينة، لا تتأثر قيمة الشركة بكيفية تمويل هذه الشركة، ولا تعتمد على سياسة توزيع الأرباح ولا على قرار جمع رأس المال عن طريق إصدار الأسهم أو بيع الديون. يستمر الدليل هنا باستخدام وسيطات التحكيم، ويعمل كمعيار لتقييم آثار العوامل خارج النموذج التي تؤثر على القيمة.

يتم توفير آلية تحديد القيمة (المؤسسية) من خلال نظرية قيمة الاستثمار (John Burr Williams)، التي تقترح أن يتم احتساب قيمة الأصل باستخدام «التقييم وفقًا لقيم القيمة الحالية». وبالتالي، بالنسبة للسهم العادي، فإن القيمة الحقيقية طويلة الأجل هي القيمة الحالية لصافي التدفقات النقدية المستقبلية، في شكل أرباح. ما يتبقى هو تحديد سعر الخصم المناسب. تظهر التطورات اللاحقة «عقلانيًا»، بمعنى رسمي، أن معدل الخصم المناسب هنا (ينبغي) يعتمد على مخاطرة الأصل بالنسبة للسوق ككل، بدلاً من تفضيلات مالكيها ؛ انظر أدناه. القيمة الحالية الصافية (NPV) هي الامتداد المباشر لهذه الأفكار التي يتم تطبيقها عادة على اتخاذ القرارات بشأن تمويل الشركات (مقدمة من جويل دين ‏ في عام 1951). للحصول على نتائج أخرى، بالإضافة إلى النماذج المحددة التي تم تطويرها هنا، راجع قائمة مواضيع «تقييم الأسهم» ضمن مخطط التمويل # تقييم التدفقات النقدية المخصومة.

تقييم السندات، في أن التدفقات النقدية (القسائم وعودة رأس المال) هي الحتمية، قد تسير بنفس الطريقة.[16] إن الامتداد الفوري ، وهو سعر السندات الخالي من التحكيم، يقوم بتخفيض كل تدفق نقدي بالسعر المشتق من السوق - أي بسعر الصفر المقابل لكل كوبون - بدلاً من المعدل الإجمالي. لاحظ أنه في العديد من المعالجات ، يسبق تقييم السندات تقييم حقوق الملكية، والتي بموجبها «التدفقات النقدية (أرباح الأسهم)» غير معروفة في حد ذاتها. يسمح Williams وما بعده بالتنبؤ به - بناءً على النسب التاريخية أو السياسة المنشورة - ثم يتم التعامل مع التدفقات النقدية باعتبارها حتمية بشكل أساسي ؛ انظر أدناه تحت نظرية تمويل الشركات #.

يتم استخدام جميع نتائج «اليقين» هذه بشكل شائع في إطار تمويل الشركات. عدم اليقين هو محور «نماذج تسعير الأصول»، على النحو التالي.

شك

بالنسبة إلى "الاختيار في حالة عدم اليقين" ، فإن الافتراضين التوأمين للعقلانية وكفاءة السوق ، كما تم تعريفه بشكل أوثق ، يؤديان إلى نظرية المحفظة الحديثة (M P T) مع نموذج تسعير الأصول الرأسمالية (CAPM) - نتيجة تستند إلى التوازن - وإلى Black-Scholes نظرية -Merton (BSM ؛ غالبًا ، ببساطة Black-S c h o l e s) لتسعير الخيار - نتيجة خالية من المراجحة. لاحظ أنه يتم احتساب أسعار المشتقات الأخيرة بحيث تكون خالية من المراجحة فيما يتعلق بأسعار الأوراق المالية الأكثر تحديدًا وتوازنًا ؛ رؤية تسعير الأصول.

باختصار ، وبشكل حدسي - ومتسق مع # التسعير والتوازن الخاليين من المراجحة أعلاه - يكون الرابط كما يلي.[17] بالنظر إلى القدرة على الاستفادة من المعلومات الخاصة ، يتم تحفيز المتداولين المهتمين بأنفسهم للحصول على معلوماتهم الخاصة والتصرف فيها. عند القيام بذلك ، يساهم المتداولون في المزيد من «الأسعار» الصحيحة ، أي الفعالة : فرضية السوق الفعالة، أو EMH (Eugene Fama ، 1965). تفترض EMH (ضمنيًا) أن متوسط التوقعات يشكل «توقعات مثالية»، أي أن الأسعار التي تستخدم جميع المعلومات المتاحة ، مطابقة لأفضل تخمين للمستقبل : افتراض التوقعات المنطقية. تسمح EMH أنه عند مواجهة معلومات جديدة ، قد يبالغ بعض المستثمرين في رد فعلهم وقد يكون رد فعلهم غير صحيح ، لكن المطلوب هو أن ردود فعل المستثمرين تتبع توزيعا طبيعيا - بحيث لا يمكن استغلال التأثير الصافي على أسعار السوق بشكل موثوق تحقيق ربح غير طبيعي. في الحدود التنافسية ، ستعكس أسعار السوق جميع المعلومات المتاحة ، ويمكن أن تتحرك الأسعار فقط استجابة للأخبار ؛ [18] وهذا ، بالطبع ، يمكن أن يكون «جيدًا» أو «سيئًا»، كبيرًا أو صغيرًا: فرضية المشي العشوائي. وبالتالي ، إذا كانت أسعار الأصول المالية فعالة (على نطاق واسع)، فلن تستمر الانحرافات عن هذه القيم (التوازن) لفترة طويلة. (انظر معامل استجابة الأرباح. (على مسارات عشوائية في أسعار الأسهم: جول رينو، 1863 ؛ لويس باشيلير، 1900 ؛ موريس كيندال، 1953 ؛ بول كوتنر، 1964.)

في ظل هذه الظروف ، يمكن عندئذ افتراض أن المستثمرين يتصرفون بطريقة عقلانية: يجب حساب قرارهم الاستثماري أو التأكد من اتباع الخسارة ؛ في المقابل ، عندما تقدم فرصة التحكيم ، يستغلها المراجحون ، مما يعزز هذا التوازن. هنا ، كما هو الحال في حالة اليقين الموضحة أعلاه ، الافتراض المحدد فيما يتعلق بالتسعير هو أن الأسعار تُحسب كقيمة حالية لتوزيعات الأرباح المستقبلية المتوقعة ، [11][12][18] حسب المعلومات المتوفرة حاليًا. ما هو مطلوب رغم ذلك هو نظرية لتحديد معدل الخصم المناسب ، أي «العائد المطلوب»، بالنظر إلى عدم اليقين هذا: يتم توفيره بواسطة MPT وCAPM الخاص به. ذات الصلة ، والعقلانية - بمعنى المراجحة في الاستغلال - تؤدي إلى ظهور بلاك سكولز ؛ قيم الخيار هنا تتفق في نهاية المطاف مع CAPM.

بشكل عام ، إذن ، بينما تدرس نظرية المحفظة كيف ينبغي للمستثمرين الموازنة بين المخاطر والعائد عند الاستثمار في العديد من الأصول أو الأوراق المالية ، فإن CAPM أكثر تركيزًا ، ويصف كيف ، في التوازن ، تحدد الأسواق أسعار الأصول فيما يتعلق بمدى خطورة هذه المخاطر. الأهم من ذلك ، ستكون هذه النتيجة مستقلة عن مستوى كره المخاطرة لدى المستثمر و/ أو وظيفة الأداة المفترضة ، وبالتالي توفير معدل خصم محدد بسهولة لصناع القرار في تمويل الشركات على النحو الوارد أعلاه ، [19] وبالنسبة للمستثمرين الآخرين. تستمر الحجة على النحو التالي: إذا كان بإمكان المرء إنشاء حدود فعالة - أي كل مجموعة من الأصول التي تقدم أفضل مستوى متوقع من العائد لمستوى المخاطرة الخاص بها ، انظر الرسم البياني - ثم يمكن تشكيل محافظ كفاءة التباين المتوسط ببساطة على أنها مزيج من حيازات الأصول الخالية من المخاطر و«محفظة السوق» (نظرية فصل صناديق الاستثمار المشتركة)، مع التخطيط هنا للتخطيط كخط لسوق المال، أو CML. بعد ذلك ، بالنظر إلى CML ، فإن العائد المطلوب على الأوراق المالية المحفوفة بالمخاطر سيكون مستقلاً عن وظيفة المرافق للمستثمر ، وسيتم تحديده فقط من خلال التغاير («بيتا») مع المخاطر الإجمالية ، أي السوق. وذلك لأن المستثمرين هنا يمكنهم بعد ذلك زيادة الفائدة من خلال الرافعة المالية بدلاً من التسعير ؛ انظر مخطط CML. كما يتضح من الصيغة جانبا ، فإن هذه النتيجة تتسق مع ما سبق ، حيث تساوي العائد بلا مخاطرة بالإضافة إلى تعديل للمخاطر.[11] (تم تقديم الحدود الفعالة بواسطة هاري ماركويتز في عام 1952. تم اشتقاق CAPM بواسطة Jack Treynor (1961، 1962)، وWilliam F. Sharpe (1964)، وJohn Lintner (1965) وJan Mossin (1966) بشكل مستقل.)

يوفر Black – Scholes نموذجًا رياضيًا لسوق مالية تحتوي على أدوات مشتقة، والمعادلة الناتجة عن سعر الخيارات الأوروبية. يتم التعبير عن النموذج باعتباره معادلة Black-Scholes ، معادلة تفاضلية جزئية تصف السعر المتغير للخيار بمرور الوقت ؛ تم اشتقاقها بافتراض وجود حركة براونية هندسيه ‏ طبيعية (انظر النموذج البراوني للأسواق المالية). تتمثل النظرة المالية الرئيسية وراء النموذج في أنه يمكن للمرء أن يحوط الخيار تمامًا عن طريق شراء وبيع الأصل الأساسي بالطريقة الصحيحة وبالتالي «التخلص من المخاطر»، مع عدم وجود تسوية للمخاطر من السعر (V ، قيمة ، أو سعر الخيار ، ينمو في خطأ رياضيات (خطأ في الصياغة): {\displaystyle <mrow class="MJX-TeXAtom-ORD"><mstyle displaystyle="true" scriptlevel="0"><mi> <math>r} </mi></mstyle></mrow> </math>r r ، معدل خالية من المخاطر. انظر معادلة بلاك شولز التفسير المالي).[6][11] هذا التحوط ، بدوره ، يعني أن هناك سعرًا واحدًا مناسبًا - بمعنى خالٍ من التحكيم - للخيار. ويتم إرجاع هذا السعر بواسطة صيغة تسعير خيار Black-Scholes. (الصيغة ، وبالتالي السعر ، تتسق مع المعادلة ، لأن الصيغة هي الحل للمعادلة. بما أن الصيغة لا تشير إلى العائد المتوقع للسهم ، فإن Black-Scholes يرث حياد المخاطر ؛ متسقة بشكل حدسي مع «القضاء على المخاطر» هنا ، ومتسقة رياضياً مع # التسعير والتوازن الخاليين من التحكيم. وبالتالي ، يمكن أيضًا اشتقاق صيغة التسعير مباشرةً من خلال التوقعات المحايدة للمخاطرة. (BSM - بحثان أساسيان في عام 1973 [20][21] - يتوافق مع «الإصدارات السابقة من صيغة» Louis Bachelier (1900) وEdward O. Thorp (1967)؛ [22] على الرغم من أن هذه كانت «اكتوارية» أكثر في نكهة ، ولم يثبت خصم محايد للمخاطر.[23] انظر أيضا بول صامويلسون (1965).[24] حقق فينزينز برونزين (1908) نتائج مبكرة للغاية ، أيضًا.)

كما ذكرنا ، يمكن إثبات أن النموذجين متسقان ؛ ثم ، كما هو متوقع ، فإن الاقتصاد المالي «الكلاسيكي» موحد. هنا ، يمكن اشتقاق معادلة Black Scholes من CAPM ، وبالتالي فإن السعر الذي يتم الحصول عليه من نموذج Black-Scholes يتسق مع العائد المتوقع من CAPM.[23][25] نظرية Black-Scholes ، على الرغم من أنها مبنية على التسعير الخالي من التحكيم ، تتفق مع تسعير الأصول الرأسمالية القائمة على التوازن. كلا النموذجين ، بدوره ، يتفقان في النهاية مع نظرية Arrow-Debreu ، ويمكن اشتقاقهما من خلال تسعير الدولة ، [6] لمزيد من التوضيح ، وإذا لزم الأمر ، فإن هذه الوحدة توضح ذلك.

ملحقات

العمل الأكثر حداثة يعمم و/ أو يمدد هذه النماذج. فيما يتعلق بتسعير الأصول ، تتم مناقشة التطورات في التسعير على أساس التوازن في إطار «نظرية المحفظة» أدناه ، في حين أن «التسعير المشتق» يتعلق بتسعير محايد من المخاطر ، أي خالي من التحكيم. فيما يتعلق باستخدام رأس المال ، تتعلق «نظرية تمويل الشركات»، بشكل أساسي ، بتطبيق هذه النماذج.

نظرية الحافظة

قطعة من معيارين عند تعظيم العائد وتقليل المخاطر في المحافظ المالية (نقاط Pareto الأمثل باللون الأحمر)
انظر أيضا: نظرية محفظة ما بعد الحداثة والتمويل الرياضي إدارة المخاطر والمحفظة: العالم ف .

تتعلق غالبية التطورات هنا بالعائد المطلوب ، أي التسعير ، وتمديد C A P M الأساسي. تقترح النماذج متعددة العوامل ، مثل نموذج Fa m a-F r e n c h ثلاثي العوامل ونموذج C a r h a r t المكون من أربعة عوامل، عوامل أخرى غير عائد السوق كما هو مناسب في التسعير. يقوم نظام C A P M in t e rt e m p o r a l وC A P M المعتمد على الاستهلاك بتمديد النموذج بشكل مشابه. من خلال اختيار محفظة i n te r t e m p o r a l ، تقوم المستثمر الآن بتحسين محفظتها بشكل متكرر. بينما يدرج إدراج الاستهلاك (بالمعنى الاقتصادي) جميع مصادر الثروة ، وليس فقط الاستثمارات القائمة على السوق ، في حساب المستثمر للعائد المطلوب.

في حين أن ما سبق يمد C A P M ، فإن نموذج الفهرس الفردي هو نموذج أكثر بساطة. إنه يفترض ، فقط ، وجود علاقة بين عوائد الأمن والسوق ، دون افتراضات اقتصادية (عديدة) أخرى. من المفيد أنه يبسط تقدير العلاقة بين الأوراق المالية ، مما يقلل بشكل كبير من المدخلات لبناء مصفوفة الارتباط اللازمة لتحسين المحفظة. تختلف نظرية تسعير المراجحة (APT ؛ ستيفن روس، 1976) بالمثل فيما يتعلق بافتراضاتها. APT «تتخلى عن فكرة أن هناك محفظة واحدة مناسبة للجميع في العالم ، و... استبدالها بنموذج توضيحي لما يدفع عائدات الأصول.» [26] تقوم بإرجاع العائد المطلوب (المتوقع) للأصل المالي كدالة خطية لمختلف عوامل الاقتصاد الكلي ، ويفترض أن المراجحة يجب أن تعيد الأصول المسعرة بشكل غير صحيح إلى خطها.

فيما يتعلق بتحسين المحفظة، فإن نموذج Black-L i t t e rm a n يغادر من نهج M a r k o w i t z الأصلي المتمثل في بناء المحافظ عبر حدود فعالة. يبدأ Black-Li t term a n بدلاً من ذلك بافتراض توازن ، ثم يتم تعديله لمراعاة «وجهات النظر» (أي الآراء المحددة حول عائدات الأصول) للمستثمر المعني للوصول إلى تخصيص أصل مخصص. حيث تعتبر العوامل الإضافية للتقلبات (التقرن ، الانحراف ...) ثم يمكن تطبيق تحليل القرار متعدد المعايير؛ هنا اشتقاق محفظة باريتو فعالة. تطبق خوارزمية الحافظة الشاملة (Thomas M. Cover) التعلم الآلي على اختيار الأصول ، والتعلم بشكل تكيفي من البيانات التاريخية. تدرك نظرية الحافظة السلوكية أن المستثمرين لديهم أهداف متنوعة وأنشئوا محفظة استثمارية تلبي مجموعة واسعة من الأهداف. تم تطبيق Copulas مؤخرًا هنا. انظر تحسين الحافظة § تحسين محفظة الأمثل للتقنيات و/ أو الأهداف الأخرى.

التسعير المشتق

شعرية ذات الحدين مع صيغ CRR

فيما يتعلق بالتسعير المشتق ، يوفر نموذج تسعير الخيارات ذات الحدين إصدارًا تقديريًا من Black-Scholes ، مفيد لتقييم الخيارات الأمريكية. النماذج المبنية من هذا النوع مبنية - على الأقل ضمنيًا - باستخدام أسعار الحالة (على النحو الوارد أعلاه)؛ فيما يتعلق بذلك ، استخدم عدد كبير من الباحثين خيارات لاستخراج أسعار الحالة لمجموعة متنوعة من التطبيقات الأخرى في الاقتصاد المالي.[6][14][25] بالنسبة إلى المشتقات المعتمدة على المسار ، يتم استخدام طرق مونت كارلو لتسعير الخيارات؛ هنا النمذجة في وقت مستمر ، ولكن بالمثل يستخدم القيمة المتوقعة للخطر المحايدة. كما تم تطوير تقنيات رقمية مختلفة أخرى. لقد تم تمديد الإطار النظري أيضًا بحيث أصبح تسعير مارتينجال الآن هو النهج القياسي. التطورات المتعلقة التعقيدات في العودة و/ أو التقلب تناقش أدناه.

بالاعتماد على هذه التقنيات ، تم تطوير نماذج مشتقة للعديد من التطبيقات الفرعية والتطبيقات الأخرى ، وكلها تستند إلى نفس المنطق (باستخدام «تحليل المطالبة الطارئة»). يسمح تقييم الخيارات الحقيقية بأنه يمكن لأصحاب الخيارات التأثير على أساس الخيار ؛ تفترض نماذج تقييم خيارات أسهم الموظف بشكل صريح عدم العقلانية من جانب أصحاب الخيارات ؛ تسمح مشتقات الائتمان بعدم الوفاء بالتزامات الدفع و/ أو متطلبات التسليم. يتم الآن تقييم المشتقات الغريبة بشكل روتيني. يتم التعامل مع وكيل الأصول المتعددة عن طريق المحاكاة أو التحليل القائم على الكوبولا.

وبالمثل ، بدايةً من أولدريتش فاسيتش (1977)، تسمح مختلف النماذج ذات المعدلات القصيرة ، وكذلك التقنيات المعتمدة على السعر الآجل H J M وB G M ، بتمديد هذه التقنيات لتشمل المشتقات ذات الدخل الثابت وأسعار الفائدة. (يعتمد طرازا V a s i c e k وCIR على التوازن ، بينما تعتمد النماذج Ho-Lee والنماذج اللاحقة على التسعير الخالي من التحكيم.) يتم تمديد تقييم السندات ذات الصلة: يسمح أسلوب حساب التفاضل والتكامل في Stochastic ، الذي يستخدم هذه الطرق ، بمعدلات «عشوائية» (مع إعادة سعر خالٍ من المراجحة ، على النحو الوارد أعلاه)؛ نماذج شعرية للأوراق المالية المختلطة تسمح بتدفقات نقدية غير حتمية (وأسعار عشوائية).

على النحو الوارد أعلاه ، اعتمد تسعير المشتقات (OTC) على إطار التسعير المحايد لمخاطر B S M ، في ظل افتراضات التمويل بسعر خالٍ من المخاطر والقدرة على تكرار التدفقات النقدية بشكل مثالي حتى يتم التحوط بالكامل. وهذا ، بدوره ، مبني على افتراض وجود بيئة خالية من مخاطر الائتمان. بعد الأزمة المالية في عام 2008 ، لذلك ، يتم إضافة مسائل مثل مخاطر الائتمان للطرف المقابل ، وتكاليف التمويل وتكاليف رأس المال ، [27] وتعديل تقييم الائتمان ، أو C V A - وتسويات تقييم محتملة أخرى ، مجتمعة x V A - تتم إضافتها عمومًا إلى القيمة المشتقة المحايدة للمخاطر.

من التغييرات ذات الصلة ، وربما الأكثر جوهرية ، أن الخصم الآن على منحنى مؤشر مبادلة Overnight ، بدلاً من L I B O R كما كان مستخدمًا من قبل. وذلك لأن ما بعد الأزمة ، يعتبر O I S وكيلًا أفضل «للمعدلات الخالية من المخاطر».[28] (وأيضًا ، من الناحية العملية ، عادة ما تكون الفائدة المدفوعة على ضمان ن قدي هي معدل الليلة الواحدة ؛ يُشار إلى خصم O I S ، في بعض الأحيان ، باسم «خصم C S A».) التسعير مبادلة - و، في الواقع، بناء منحنى - يتم تعديل أبعد من ذلك: في السابق، وبلغت قيمة المبادلات قبالة «خصم النفس» منحنى أسعار الفائدة واحد؛ في حين أنه بعد الأزمة ، لاستيعاب خصم O I S ، أصبح التقييم الآن ضمن إطار «متعدد المنحنى» حيث يتم إنشاء «منحنيات التنبؤ» لكل فترة L I B O R عائمة ، مع خصم على منحنى O I S مشترك ؛ انظر مقايضة سعر الفائدة التقييم والتسعير.

نظرية تمويل الشركات

تقييم المشروع عبر شجرة القرار.

تم تمديد نظرية تمويل الشركات أيضًا: تعكس التطورات المذكورة أعلاه وتقييم الأصول واتخاذ القرارات بعد الآن «اليقين». كما تمت مناقشته ، فإن طرق مونت كارلو في مجال التمويل ، التي طرحها ديفيد بي. هيرتز في عام 1964، تسمح للمحللين الماليين بإنشاء نماذج «تمويل عشوائية أو احتمالية للشركات»، على عكس النماذج الثابتة والحتمية التقليدية ؛ [29] انظر تمويل الشركات قياس عدم اليقين. ذات الصلة ، تسمح نظرية الخيارات الحقيقية للمالك - أي الإجراءات الإدارية - التي تؤثر على القيمة الأساسية: من خلال دمج منطق تسعير الخيارات ، يتم تطبيق هذه الإجراءات بعد ذلك على توزيع النتائج المستقبلية ، مع التغيير مع الوقت ، والتي تحدد بعد ذلك تقييم «المشروع» اليوم.[30]

وبشكل أكثر تقليدية ، تم استخدام أشجار القرارات - التي تكمل بعضها البعض - لتقييم المشروعات ، من خلال دمجها في التقييم (جميع) الأحداث (أو الولايات) المحتملة وقرارات الإدارة المترتبة عليها ؛ [29][31] معدل الخصم الصحيح هنا يعكس «كل نقطة غير قابلة للتنوع تتطلع إلى الأمام».[29] (هذه التقنية تسبق استخدام خيارات حقيقية في تمويل الشركات ؛ [32] فهي مستعارة من بحوث العمليات، وليست «تنمية اقتصادية مالية» في حد ذاتها.)

يرتبط هذا ، هو التدفقات النقدية المتوقعة في تقييم الأسهم. في كثير من الحالات ، بعد وليامز أعلاه ، تم تخفيض متوسط (أو على الأرجح) التدفقات النقدية ، [33] بدلاً من معاملة أكثر صحة لكل ولاية في ظل عدم اليقين ؛ انظر التعليقات تحت النمذجة المالية § المحاسبة. في العلاجات الأكثر حداثة ، إذن ، فإن التدفقات النقدية المتوقعة (بالمعنى الرياضي) مجتمعة في القيمة الإجمالية لكل فترة تنبؤية يتم خصمها.[29][34][35][36] وباستخدام C A P M - أو الامتدادات - يكون الخصم هنا بسعر خالٍ من المخاطر بالإضافة إلى علاوة مرتبطة بعدم اليقين في التدفقات النقدية للمشروع أو المشروع.[29][35]

تتضمن التطورات الأخرى هنا [37] نظرية الوكالة، التي تحلل الصعوبات في تحفيز إدارة الشركات («الوكيل») للعمل بما يحقق مصلحة المساهمين («الموكل»)، وليس لمصالحهم الخاصة. توفر محاسبة الفوائض النظيفة وتقييم الدخل المتبقي ذي الصلة نموذجًا يعيد السعر كدالة للأرباح والعوائد المتوقعة والتغيير في القيمة الدفترية، بدلاً من توزيعات الأرباح. ينشأ هذا النهج ، إلى حد ما ، بسبب التناقض الضمني في رؤية القيمة كدالة لتوزيعات الأرباح ، مع الإبقاء أيضًا على أن سياسة توزيع الأرباح لا يمكن أن تؤثر على القيمة وفقًا لمبدأ Modigliani وMiller «مبدأ عدم الصلة»؛ انظر سياسة توزيع الأرباح عدم أهمية سياسة توزيع الأرباح.

التطبيق النموذجي للخيارات الحقيقية هو مشاكل نوع الميزانية الرأسمالية كما هو موضح. ومع ذلك ، يتم تطبيقها أيضًا على مسائل هيكل رأس المال وسياسة توزيع الأرباح ، وعلى التصميم ذي الصلة لأوراق مالية الشركات ؛ [38] وبما أن حاملي الأسهم والسندات لديهم وظائف موضوعية مختلفة ، في تحليل مشاكل الوكالة ذات الصلة.[30] في جميع هذه الحالات ، يمكن أن توفر الأسعار الحكومية المعلومات الضمنية في السوق المتعلقة بالشركة ، على النحو الوارد أعلاه ، والتي يتم تطبيقها بعد ذلك على التحليل. على سبيل المثال ، يمكن (يجب) تسعير السندات القابلة للتحويل بما يتفق مع الأسعار الحكومية لأسهم الشركة.[13][34]

التحديات والنقد

كما ذكر أعلاه ، هناك صلة وثيقة للغاية بين (1) فرضية المشي العشوائي ، مع التوقعات المرتبطة بأن تغيرات الأسعار يجب أن تتبع التوزيع الطبيعي، من ناحية ، و (2) كفاءة السوق والتوقعات المنطقية، من ناحية أخرى. لاحظ ، مع ذلك ، أنه يتم ملاحظة حالات الخروج (الواسعة) عن هذه ، وبالتالي ، هناك ، على التوالي ، مجموعتان رئيسيتان من التحديات.

المغادرين من الحياة الطبيعية

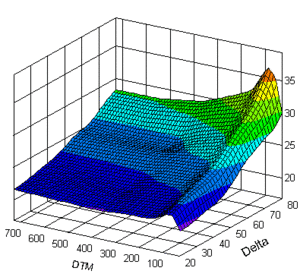
سطح التقلب الضمني. يمثل المحور Z تقلبًا ضمنيًا في المئة ، وتمثل محاور X وY دلتا الخيار ، والأيام حتى الاستحقاق.

كما تمت مناقشته ، فإن الافتراضات القائلة بأن أسعار السوق تتبع مسارًا عشوائيًا و/ أو أن عوائد الأصول يتم توزيعها بشكل طبيعي هي أمور أساسية. ومع ذلك ، تشير الدلائل التجريبية إلى أن هذه الافتراضات قد لا تصمد (انظر خطر التعرق ، مخاطر الانحراف ، الذيل الطويل) وأنه في الممارسة العملية ، يعدل التجار والمحللون ومديرو المخاطر بشكل متكرر «النماذج القياسية» (انظر نموذج المخاطر). في الواقع ، اكتشف B e n o i t Mandelbrot بالفعل في الستينيات من القرن الماضي أن التغيرات في الأسعار المالية لا تتبع توزيعًا غوسيًا، وهو الأساس لنظرية تسعير الخيارات ، على الرغم من أن هذه الملاحظة كانت بطيئة في العثور على طريقها إلى الاقتصاد المالي السائد.

تم تقديم نماذج مالية ذات توزيعات طويلة الذيل وتجمعات متقلبة للتغلب على مشاكل الواقعية للنماذج المالية «الكلاسيكية» أعلاه ؛ بينما تسمح نماذج الانتقال السريع لأسعار (الخيار) بدمج "القفزات" في السعر الفوري.[39] وبالمثل ، يستكمل مديرو المخاطر (أو البديل) القيمة القياسية في نماذج المخاطر بمحاكاة تاريخية، ونماذج خليط، وتحليل مكون رئيسي، ونظرية القيمة القصوى، فضلاً عن نماذج لتجميع التقلب.[40] لمزيد من المناقشة رؤية الذيل الدهون § التوزيع التطبيقات في الاقتصاد ، والقيمة المعرضة للخطر النقد. مديرو الحافظة ، وبالمثل ، قاموا بتعديل معايير وخوارزميات التحسين الخاصة بهم ؛ انظر نظرية محفظة # أعلاه.

يرتبط ارتباطًا وثيقًا بابتسامة التقلب، حيث يُلاحظ أن التقلب الضمني - التقلب المقابل لسعر B S M - يختلف كدالة لسعر الإضراب (أي النقود)، وهذا صحيح فقط إذا كان توزيع تغيير السعر غير طبيعي ، على عكس ذلك المفترض بواسطة B S M. يصف مصطلح مصطلح التقلب مدى اختلاف التقلب (الضمني) بالنسبة للخيارات ذات الصلة مع آجال استحقاق مختلفة. سطح التقلب الضمني هو ثم مؤامرة سطح ثلاثية الأبعاد من ابتسامة التقلب وهيكل المدى. هذه الظواهر التجريبية تنفي افتراض التقلب المستمر والسجلات الطبيعية - التي بنيت عليها بلاك سكولز ؛ [22][39] انظر نموذج بلاك سكولز تقلب ابتسامة.

نتيجة لذلك ، يستخدم المتداولون (ومديرو المخاطر) نماذج «متسقة مع الابتسامة»، أولاً ، عند تقييم المشتقات التي لم يتم تعيينها مباشرة إلى السطح ، مما يسهل تسعير المجموعات الأخرى ، مثل مجموعات الأسعار / النضج غير المشتقة ، أو المشتقات غير الأوروبية ، وعموما لأغراض التحوط. الطريقتان الرئيسيتان هما التقلب المحلي وتقلب مؤشر ستوكاستيك. الأول يعيد التقلبات «المحلية» إلى كل نقطة زمنية محددة للتقييم القائم على الفروق أو المحاكاة - أي على عكس التذبذب الضمني ، والذي يبقى ثابتًا بشكل عام. وبهذه الطريقة ، تكون الأسعار المحسوبة - والهياكل الرقمية - متسقة مع السوق بطريقة خالية من المراجحة. النهج الثاني يفترض أن تقلب السعر الأساسي هو عملية عشوائية وليس ثابتة. يتم أولاً "معايرة" النماذج هنا للأسعار المرصودة ، ثم يتم تطبيقها على التقييم المعني ؛ الأكثر شيوعًا هي H e s t o n وS A B R وC E V. يعالج هذا النهج بعض المشكلات المحددة مع التحوط في ظل التقلبات المحلية.[41]

تتعلق التقلبات المحلية بالأشجار الضمنية ذات الحدين والأشجار المستندة إلى شعرية - تقديرا أساسيا للنهج - والتي تستخدم بالمثل في التسعير هذه مبنية على أسعار الدولة المستردة من السطح. تسمح أشجار E d g e w o r t h ذات الحدين بوجود انحراف وخرط محدد (أي غير غاوسي) في السعر الفوري ؛ بسعر هنا ، فإن الخيارات ذات الضربات المختلفة ستعيد التقلبات الضمنية المختلفة ، ويمكن معايرة الشجرة حسب الابتسامة على النحو المطلوب.[42] كما تم تطوير نماذج مقفلة ذات أغراض مماثلة.[43]

كما ذكر أعلاه ، يفترض B S M - ونماذج المشتقات الأخرى عادة - (د) القدرة على تكرار التدفقات النقدية تمامًا بحيث يتم التحوط بالكامل ، ومن ثم إلى الخصم دون معدل المخاطرة. وهذا ، بدوره ، مبني على افتراض وجود بيئة خالية من مخاطر الائتمان. بعد الأزمة ، إذن ، يتم إجراء العديد من التعديلات على القيمة x على القيمة المشتقة من المخاطر المحايدة. لاحظ أن هذه العناصر إضافية لأي تأثير على الابتسامة أو السطح: هذا صحيح لأن السطح مبني على بيانات الأسعار المتعلقة بالمراكز المضمونة بالكامل ، وبالتالي لا يوجد «حساب مزدوج» لمخاطر الائتمان (وما إلى ذلك) عند تضمين x V A. (أيضًا ، لو لم يكن الأمر كذلك ، فسيكون لكل طرف مقابل سطحه الخاص.. .)

المغادرين من العقلانية

الشذوذ في السوق والألغاز الاقتصادية
  • تأثير التقويم
    • تأثير يناير
    • سانتا كلوز تجمع
    • بيع في مايو
  • لغز نهاية مغلقة الصندوق
  • لغز الارباح
  • الإنصاف لغز المنزل التحيز
  • لغز قسط الأسهم
  • إلى الأمام الشذوذ قسط
  • انخفاض الشذوذ الشذوذ
  • الزخم الشذوذ
  • بعد إعلان الأرباح الانجراف
  • الألغاز الحقيقية لسعر الصرف

كما رأينا ، هناك افتراض شائع هو أن صناع القرار المالي يتصرفون بعقلانية. رؤية هومو الاقتصادية. لكن في الآونة الأخيرة ، تحدى الباحثون في الاقتصاد التجريبي والتمويل التجريبي هذا الافتراض تجريبياً. كما يتم تحدي هذه الافتراضات من الناحية النظرية، من خلال التمويل السلوكي، وهو مجال يتعلق في المقام الأول بالقيود المفروضة على عقلانية العوامل الاقتصادية.

تمشيا مع هذه النتائج ومكملة لها ، تم توثيق العديد من الحالات الشاذة المستمرة في السوق ، والتي تمثل تشوهات في الأسعار و/ أو العودة - على سبيل المثال أقساط الحجم - والتي تتعارض مع فرضية السوق الفعالة؛ تأثيرات التقويم هي أفضل مجموعة معروفة هنا. تتعلق هذه الألغاز الاقتصادية المختلفة ، المتعلقة بالظواهر التي تتناقض مع النظرية بالمثل. ينشأ لغز علاوة الأسهم ، على سبيل المثال ، في أن الفرق بين العوائد الملحوظة على الأسهم مقارنة بالسندات الحكومية أعلى باستمرار من عائد المخاطرة في الأسهم العقلانية التي ينبغي على المستثمرين طلبها ، وهو «عائد غير طبيعي». للحصول على مزيد من السياق ، انظر فرضية المشي العشوائي § فرضية المشي العشوائية، والشريط الجانبي لحالات محددة.

بشكل أعم ، وخاصة بعد الأزمة المالية في 2007-2010 ، تعرض الاقتصاد المالي والتمويل الرياضي إلى نقد أعمق ؛ جدير بالذكر هنا نسيم نيكولاس طالب، الذي يدعي أن أسعار الأصول المالية لا يمكن وصفها بالنماذج البسيطة المستخدمة حاليًا ، مما يجعل الكثير من الممارسات الحالية غير ذات صلة ، وفي أسوأ الأحوال ، مضللة بشكل خطير ؛ رؤية نظرية البجعة السوداء، توزيع طالب. كان موضوع الاهتمام العام الذي تمت دراسته في السنوات الأخيرة هو الأزمات المالية، [44] وفشل الاقتصاديات المالية في تشكيلها. (المشكلة ذات الصلة هي المخاطر النظامية: حيث تحتفظ الشركات بأوراق مالية فيما بينها ، فإن الترابط قد يستلزم «سلسلة تقييم» - وأداء شركة واحدة ، أو أمان ، سوف يؤثر هنا على الجميع ، وهي ظاهرة لا يمكن صياغتها بسهولة ، بغض النظر عما إذا النماذج الفردية صحيحة. انظر المخاطر النظامية § عدم كفاية نماذج التقييم الكلاسيكية؛ شلالات في الشبكات المالية؛ رحلة إلى الجودة.)

تشمل مجالات البحث التي تحاول شرح (أو على الأقل نموذج) هذه الظواهر والأزمات ، [12] تجارة الضوضاء والبنية المجهرية للسوق ونماذج العوامل غير المتجانسة. يمتد هذا الأخير إلى الاقتصاد الحسابي القائم على الوكيل، حيث يتم التعامل مع السعر كظاهرة ناشئة، الناتجة عن تفاعل مختلف المشاركين في السوق (الوكلاء). تقول فرضية السوق الصاخبة أن الأسعار يمكن أن تتأثر بالمضاربين وتجار الزخم ، وكذلك من الداخل والمؤسسات التي غالباً ما تشتري وتبيع الأسهم لأسباب لا علاقة لها بالقيمة الأساسية ؛ انظر الضوضاء (الاقتصادية). فرضية السوق التكيفية هي محاولة للتوفيق بين فرضية السوق الفعالة والاقتصاد السلوكي ، من خلال تطبيق مبادئ التطور على التفاعلات المالية. بدلاً من ذلك ، تُظهر سلسلة المعلومات المشاركين في السوق وهم يشاركون في نفس أفعال الآخرين («سلوك القطيع»)، على الرغم من التناقضات مع معلوماتهم الخاصة. وقد تم تطبيق النمذجة المستندة إلى Copula بالمثل. انظر أيضًا "فرضية عدم الاستقرار المالي" التي وضعها هيمان مينسكي، بالإضافة إلى مقاربة جورج سوروس، الانعكاسية ، الأسواق المالية ، والنظرية الاقتصادية.

ولكن على الجانب الآخر ، أظهرت العديد من الدراسات أنه على الرغم من هذه الانحرافات عن الكفاءة ، إلا أن أسعار الأصول عادةً ما تمشي بشكل عشوائي ، وبالتالي لا يمكن للمرء أن يتفوق باستمرار على متوسطات السوق («ألفا»).[45] لذلك فإن الأثر العملي هو أن الاستثمار السلبي (على سبيل المثال من خلال صناديق المؤشرات منخفضة التكلفة) ينبغي ، في المتوسط ، أن يخدم بشكل أفضل من أي إستراتيجية نشطة أخرى.[46] تعد لعبة Burton M a l k i e l للمشي العشوائي في وول ستريت - التي نُشرت لأول مرة في عام 1973، وفي عددها الحادي عشر اعتبارًا من عام 2015 - تعميمًا شائعًا لهذه الحجج. (راجع أيضًا جون س. بوغل 's Sense على صناديق الاستثمار المشتركة ؛ لكن قارن وارين بافيت من S u p e r i n v e s t o r s لـ Graham-and-D o d d s v i l l e. لاحظ أيضًا أن الحدود الموروثة مؤسسيًا للمراجحة - على عكس العوامل المتناقضة مباشرة مع النظرية - تُقترح أحيانًا كتفسير لهذه الانحرافات عن الكفاءة.

انظر أيضا

المراجع

  1. ^ أ ب William F. Sharpe, "Financial Economics" , in "Macro-Investment Analysis". Stanford University (manuscript). مؤرشف من الأصل في 2014-07-14. اطلع عليه بتاريخ 2009-08-06.
  2. ^ أ ب ميرتون ميلر ، (1999). تاريخ المالية: حساب شاهد عيان ، مجلة إدارة المحافظ. صيف 1999.
  3. ^ Robert C. Merton "Nobel Lecture" (PDF). مؤرشف من الأصل (PDF) في 2009-03-19. اطلع عليه بتاريخ 2009-08-06.
  4. ^ e.g.: Kent نسخة محفوظة 2014-02-21 على موقع واي باك مشين.; City London نسخة محفوظة 2014-02-23 على موقع واي باك مشين.; UC Riverside نسخة محفوظة 2014-02-22 على موقع واي باك مشين.; Leicester نسخة محفوظة 2014-02-22 على موقع واي باك مشين.; Toronto نسخة محفوظة 2014-02-21 على موقع واي باك مشين.; UMBC نسخة محفوظة 2014-12-30 على موقع واي باك مشين.
  5. ^ For example, http://www.dictionaryofeconomics.com/search_results?q=&field=content&edition=all&topicid=G00 نسخة محفوظة 2013-05-29 على موقع واي باك مشين..
  6. ^ أ ب ت ث ج ح خ د ذ روبنشتاين ، مارك. (2005). "لحظات عظيمة في الاقتصاد المالي: رابعا. النظرية الأساسية (الجزء الأول)" ، مجلة إدارة الاستثمار ، المجلد. 3 ، رقم 4 ، الربع الرابع 2005 ؛ ~ (2006). الجزء الثاني ، المجلد. 4 ، رقم 1 ، الربع الأول 2006. انظر تحت عنوان "الروابط الخارجية".
  7. ^ C. Lewin (1970). An early book on compound interest نسخة محفوظة 2016-12-21 على موقع واي باك مشين., Institute and Faculty of Actuaries
  8. ^ انظر روبنشتاين تحت عنوان "الببليوغرافيا".
  9. ^ Emanuel Derman, A Scientific Approach to CAPM and Options Valuation نسخة محفوظة 2016-03-30 على موقع واي باك مشين.[وصلة مكسورة]
  10. ^ أ ب Freddy Delbaen and Walter Schachermayer. (2004). "What is... a Free Lunch?" نسخة محفوظة 2016-03-04 على موقع واي باك مشين. (pdf). Notices of the AMS 51 (5): 526–528
  11. ^ أ ب ت ث Christopher L. Culp and جون إتش كوكرين. (2003). ""Equilibrium Asset Pricing and Discount Factors: Overview and Implications for Derivatives Valuation and Risk Management" نسخة محفوظة 2016-03-04 على موقع واي باك مشين., in Modern Risk Management: A History. Peter Field, ed. London: Risk Books, 2003. (ردمك 1904339050)
  12. ^ أ ب ت ث Farmer J. Doyne, Geanakoplos John (2009). "The virtues and vices of equilibrium and the future of financial economics" (PDF). Complexity. ج. 14 ع. 3: 11–38. arXiv:0803.2996. Bibcode:2009Cmplx..14c..11F. DOI:10.1002/cplx.20261. مؤرشف من الأصل (PDF) في 2020-03-17.
  13. ^ أ ب ت انظر de Matos ، وكذلك Bossaerts وØdegaard ، تحت المراجع.
  14. ^ أ ب Don M. Chance (2008). "Option Prices and State Prices" نسخة محفوظة 2012-02-09 على موقع واي باك مشين.
  15. ^ Breeden، Douglas T.؛ Litzenberger، Robert H. (1978). "Prices of State-Contingent Claims Implicit in Option Prices". Journal of Business. ج. 51 ع. 4: 621–651. DOI:10.1086/296025. JSTOR:2352653.
  16. ^ أ ب انظر لوينبرجر علوم الاستثمار ، تحت المراجع.
  17. ^ للحصول على علاج أكثر رسمية ، انظر ، على سبيل المثال: يوجين فاما. 1965. يسير عشوائي في أسعار البورصة. مجلة المحللين الماليين ، سبتمبر / أكتوبر 1965 ، المجلد. 21 ، رقم 5: 55-59. "نسخة مؤرشفة". مؤرشف من الأصل في 2018-11-19. اطلع عليه بتاريخ 2019-04-20.{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)
  18. ^ أ ب Shiller، Robert J. (2003). "From Efficient Markets Theory to Behavioral Finance" (PDF). Journal of Economic Perspectives. ج. 17 ع. 1 (Winter 2003): 83–104. DOI:10.1257/089533003321164967. مؤرشف (PDF) من الأصل في 2015-04-12.
  19. ^ ميخائيل س. جنسن and Smith، Clifford W.، "Theory of Corporate Finance: A Historical Overview". In: The Modern Theory of Corporate Finance ، New York: McGraw-Hill Inc.، pp. 2-20، 1984.
  20. ^ Black، Fischer؛ Myron Scholes (1973). "The Pricing of Options and Corporate Liabilities". Journal of Political Economy. ج. 81 ع. 3: 637–654. DOI:10.1086/260062. [1]
  21. ^ Merton، Robert C. (1973). "Theory of Rational Option Pricing". Bell Journal of Economics and Management Science. ج. 4 ع. 1: 141–183. DOI:10.2307/3003143. JSTOR:3003143. [2] نسخة محفوظة 27 أبريل 2019 على موقع واي باك مشين.
  22. ^ أ ب Haug, E. G. and Taleb, N. N. (2008): Why We Have Never Used the Black-Scholes-Merton Option Pricing Formula نسخة محفوظة 2011-05-03 على موقع واي باك مشين., Wilmott Magazine January 2008
  23. ^ أ ب Emanuel Derman, A Scientific Approach to CAPM and Options Valuation نسخة محفوظة 30 مارس 2016 على موقع واي باك مشين.[1] نسخة محفوظة 2016-03-30 على موقع واي باك مشين.
  24. ^ Samuelson Paul (1965). "A Rational Theory of Warrant Pricing" (PDF). Industrial Management Review. ج. 6: 2. مؤرشف (PDF) من الأصل في 2017-03-01. اطلع عليه بتاريخ 2017-02-28.
  25. ^ أ ب Don M. Chance (2008). "Option Prices and Expected Returns" نسخة محفوظة 2015-09-23 على موقع واي باك مشين.
  26. ^ نظرية التسعير للتحكيم ، الفصل السادس في جوتزمان ، تحت الروابط الخارجية
  27. ^ "Post-Crisis Pricing of Swaps using xVAs" نسخة محفوظة 2016-09-17 على موقع واي باك مشين., Christian Kjølhede & Anders Bech, Master thesis, Aarhus University
  28. ^ Hull، John؛ White، Alan (2013). "LIBOR vs. OIS: The Derivatives Discounting Dilemma". Journal of Investment Management. ج. 11 ع. 3: 14–27.
  29. ^ أ ب ت ث ج Aswath Damodaran (2007). "Probabilistic Approaches: Scenario Analysis, Decision Trees and Simulations". In Strategic Risk Taking: A Framework for Risk Management. Prentice Hall. (ردمك 0137043775) "نسخة مؤرشفة" (PDF). مؤرشف من الأصل في 2020-03-08. اطلع عليه بتاريخ 2020-04-06.{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)
  30. ^ أ ب Damodaran، Aswath (2005). "The Promise and Peril of Real Options" (PDF). NYU Working Paper ع. S-DRP-05-02. مؤرشف (PDF) من الأصل في 2001-06-13. اطلع عليه بتاريخ 2016-12-14.
  31. ^ Smith، James E.؛ Nau، Robert F. (1995). "Valuing Risky Projects: Option Pricing Theory and Decision Analysis" (PDF). Management Science. ج. 41 ع. 5: 795–816. DOI:10.1287/mnsc.41.5.795. مؤرشف (PDF) من الأصل في 2010-06-12. اطلع عليه بتاريخ 2017-08-17.
  32. ^ See for example: Magee، John F. (1964). "Decision Trees for Decision Making". هارفارد بزنس ريفيو. July 1964: 795–816. مؤرشف من الأصل في 2017-08-16. اطلع عليه بتاريخ 2017-08-16.
  33. ^ Kritzman، Mark (2017). "An Interview with Nobel Laureate Harry M. Markowitz". Financial Analysts Journal. ج. 73 ع. 4: 16–21. DOI:10.2469/faj.v73.n4.3.
  34. ^ أ ب انظر Kruschwitz وLöffler لكل ببليوغرافيا.
  35. ^ أ ب "Capital Budgeting Applications and Pitfalls" نسخة محفوظة 2017-08-15 على موقع واي باك مشين.. Ch 13 in إيفو ويلش (2017). Corporate Finance: 4th Edition[وصلة مكسورة]
  36. ^ George Chacko and Carolyn Evans (2014). Valuation: Methods and Models in Applied Corporate Finance. FT Press. (ردمك 0132905221)
  37. ^ انظر جنسن وسميث تحت عنوان "الروابط الخارجية" ، وكذلك روبنشتاين تحت عنوان "المراجع"
  38. ^ Kenneth D. Garbade (2001). Pricing Corporate Securities as Contingent Claims. ميت بريس. (ردمك 9780262072236)
  39. ^ أ ب Black، Fischer (1989). "How to use the holes in Black-Scholes". Journal of Applied Corporate Finance. ج. 1 ع. Jan: 67–73. DOI:10.1111/j.1745-6622.1989.tb00175.x.
  40. ^ III.A.3 in Carol Alexander, ed. The Professional Risk Managers' Handbook: A Comprehensive Guide to Current Theory and Best Practices. PRMIA Publications (January 2005). (ردمك 978-0976609704)
  41. ^ Hagan، Patrick؛ وآخرون (2002). "Managing smile risk". Wilmott Magazine ع. Sep: 84–108.
  42. ^ See for example Pg 217 of: Jackson, Mary; Mike Staunton (2001). Advanced modelling in finance using Excel and VBA. New Jersey: Wiley. (ردمك 0-471-49922-6).
  43. ^ وتشمل هذه: Jarrow وRudd (1982) ؛ Corrado and Su (1996)؛ Backus وForesi وWu (2004). انظر: Emmanuel Jurczenko ، Bertrand Maillet & Bogdan Negrea ، 2002. "إعادة النظر في نماذج تسعير الخيار التقريبي متعدد اللحظات: مقارنة عامة (الجزء 1)". ورقة عمل ، كلية لندن للاقتصاد والعلوم السياسية.
  44. ^ From The New Palgrave Dictionary of Economics, Online Editions, 2011, 2012, with abstract links:

       • "regulatory responses to the financial crisis: an interim assessment" نسخة محفوظة 2013-05-29 على موقع واي باك مشين. by Howard Davies

       • "Credit Crunch Chronology: April 2007–September 2009" نسخة محفوظة 2013-05-29 على موقع واي باك مشين. by The Statesman's Yearbook team

       • "Minsky crisis" نسخة محفوظة 2013-05-29 على موقع واي باك مشين. by إل. راندال راي

       • "euro zone crisis 2010" نسخة محفوظة 2013-05-29 على موقع واي باك مشين. by دانيال قروس and Cinzia Alcidi.

       • Carmen M. Reinhart and Kenneth S. Rogoff, 2009. This Time Is Different: Eight Centuries of Financial Folly, Princeton. Description نسخة محفوظة 2013-01-18 على موقع واي باك مشين., ch. 1 ("Varieties of Crises and their Dates". pp. 3-20) نسخة محفوظة 2012-09-25 على موقع واي باك مشين., and chapter-preview links.
  45. ^ William F. Sharpe (1991). "The Arithmetic of Active Management" نسخة محفوظة 2013-11-13 على موقع واي باك مشين.. Financial Analysts Journal Vol. 47, No. 1, January/February
  46. ^ William F. Sharpe (2002). Indexed Investing: A Prosaic Way to Beat the Average Investor نسخة محفوظة 2013-11-14 على موقع واي باك مشين.. Presention: Monterey Institute of International Studies. Retrieved May 20, 2010.
مجلوبة من «https://3rabica.org/index.php?title=اقتصاد_مالي&oldid=2668479»