لوغاريتم

لوغاريتم
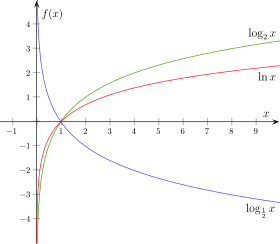تمثيل اللوغاريتمات، فاللون الأحمر ذو الأساس (e)، واللون الاخضر ذو الأساس 2، واللون الأزرق ذو الأساس 1/2، نلاحظ أن جميع المنحنيات قطعت النقطة x = 1. تمثيل اللوغاريتمات، فاللون الأحمر ذو الأساس (e)، واللون الاخضر ذو الأساس 2، واللون الأزرق ذو الأساس 1/2، نلاحظ أن جميع المنحنيات قطعت النقطة x = 1.
تدوين	${\log }_a(x)$
دالة عكسية	$a^x(x)$
مشتق الدالة	$\frac{1}{x\ln (a)}$
مشتق عكسي (تكامل)	$\frac{x\ln (x)-x}{\ln a}+C$ أو:$x{\log }_{a}x-x{\log }_{a}e+C$
الميزات الأساسية
مجال الدالة	${\mathbb{R}}_{+}^{*}$
المجال المقابل	$\mathbb{R}$
قيم محددة
القيمة/النهاية عند الصفر	على اليمين: $-\mathrm{\infty }$ إذا كان $a>1$ $+\mathrm{\infty }$ إذا كان $a<1$
نهاية الدالة عند +∞	$+\mathrm{\infty }$ إذا كان $a>1$ $-\mathrm{\infty }$ إذا كان $a<1$
القيمة/النهاية عند 1	0
القيمة/النهاية عند $a$	1
خطوط مقاربة	$x=0$
جذور الدالة	1

في الرياضيات اللوغاريتم أو اللوغاريثم (بالإنجليزية: logarithm)‏ هي الدالة العكسية للدوال الأسية ويُعرَّف لوغاريتم عدد ما بالنسبة لأساس ما، بأنه الأس المرفوع على الأساس والذي سينتج ذلك العدد. فعلى سبيل المثال فلوغاريتم 1000 بالنسبة للأساس 10 هو 3 لأن 1000 = 10 × 10 × 10 = 10³. وعموما، يمكن القول أنه إذا كان x = b^y فإن لوغاريتم x بالنسبة للأساس b هو y يعبر عن ذلك رياضياً بالعلاقة:

log_b x=y

وبالرجوع إلى المثال يصبح:

log₁₀(1000) = 3.

يعرف اللوغاريتم العشري بأنه لوغاريتم عدد ما بالنسبة للأساس 10 والذي يستخدم بشكل كبير في حساب التطبيقات العلمية والهندسية. الأسس أو اللوغاريتم هي العملية العكسية للدوال الأسية ويُعرَّف اللوغاريتم الطبيعي بأنه لوغاريتم عدد بالنسبة لأساس هو العدد النيبيري (e) والذي له تطبيقات كثيرة في الحسابات الهندسية والعلمية وفي الرياضيات البحتة وخاصة في التفاضل والتكامل. في حين يعرف اللوغاريتم الثنائي لعدد ما بأنه لوغاريتمه بالنسبة للأساس 2 ويستخدم بشكل كبير في علم الحاسوب والدارات المنطقية.

كان اللوغارتم معروفا لدى العرب نسبة إلى العالم الخوارزمي، ولقد أدخل مفهوم اللوغاريتمات إلى الرياضيات في أوائل القرن السابع عشر على يد العالم جون نابير وسيلةً لتبسيط الحسابات، ليعتمد عليها بعد ذلك الملاحون والعلماء والمهندسون والفلكيون وغيرهم لإنجاز حساباتهم بسهولة أكبر، مستخدمين المساطر الحاسبة والجداول اللوغاريتمية. وتعود كلمة اللوغارتم إلى العالم العربي الخوارزمي حيث يرد أسمه في اللغة الإنجليزية بكلمة Algorism وalgorithm واللتان تنبعان من كلمة Algoritmi، الشكل اللاتيني لاسمه الخوارزمي. كما استفادوا من خواص اللوغاريتمات باستبدال عمليات الضرب لإيجاد لوغاريتم جداء عددين بخاصية الجمع وفق الخاصية:

${\log }_b(xy)={\log }_b(x)+{\log }_b(y).$

قام ليونهارت أويلر في القرن الثامن عشر بربط مفهوم اللوغاريتمات بمفهوم التابع الأسي ليتوسع مفهوم اللوغاريتمات ويرتبط بالتوابع.

كما يستفاد من المقياس اللوغاريتمي من التقليل من التمثيل البياني لمجالات واسعة من الكميات إلى مقياس أصغر. فعلى سبيل المثال الديسيبل هو وحدة لوغاريتمية لقياس ضغظ الصوت ونسبة الفولت. كما يستخدم الأس الهيدروجيني (وهو مقياس لوغاريتمي) في الكيمياء لتحديد حمضية محلول ما وذلك من خلال العلاقة التالية:

$\mathrm{p}\mathrm{H}=\mathrm{-}\log \mathrm{[}{H}_3{\mathrm{O}}^{+}\mathrm{]}$

الأساس والتعريف

لقد أتت فكرة اللوغاريتم على أنها العملية العكسية للرفع، وهي رفع رقم لأس، على سبيل المثال رفع الرقم 2 للأس 3 هو 8، لأن الـ 8 تنتج عن ضرب 2 بنفسها 3 مرات أي:

$2^3=2\times 2\times 2=8.$

وبالتالي تكون العملية العكسية للرفع هي : لوغاريتم الـ 8 بالنسبة للأساس 2 هي 3 أي:

log₂ 8 = 3.

الرفع

يمكننا القول أن ناتج رفع رقم ما b إلى الأس 3 هو حاصل ضرب الرقم b بنفسه ثلاث مرات، وبالتعميم فإن ناتج رفع الرقم b إلى الأس n هو حاصل ضرب b بنفسه n مرة أي:

$b^n=\underset{n\text{factor}}{\underbrace{b1\times b2\times \cdots \times bn}}.$

التعريف

يعرف لوغاريتم عدد ما x بالنسبة للأساس b بأنه الأس الذي يجب أن يرفع له b لينتج عنه x أو يمكننا القول بأن لوغاريتم x بالنسبة للأساس b هو الأس y في المعادلة:

$b^y=x.$

وتكتب العبارة (لوغاريتم x بالنسبة للأساس b) رياضياً بالشكل:

${\log }_b(x)$

وناتج هذه المعادلة هو الأس y

${\log }_b(x)=y$

ولتعريف اللوغاريتم يجب أن يكون الأساس عدد حقيقي موجب لايساوي الصفر وx عدد موجب.

الحساب

من السهل حساب اللوغاريتم في بعض الحالات، مثل log10(1,000) = 3. لكن بالعموم يمكن حساب اللوغاريتم باستخدام متسلسلة القوى أو باستخدام الهندسة الحسابية بالوسائل التقريبية أو من خلال ايجاده تقريبياً من خلال الجداول اللوغاريتمية. كما تستخدم طريقة نيوتن-رافسون التكرارية في حساب اللوغاريتم لأن استخدام هذه الطريقة تمكن من ايجاد التابع العكسي والتابع الأسي بشكل فعال. وتستخدم طريقة منزلة بمنزلة لحساب اللوغاريتمات إذا كانت العملية المتاحة فقط هي إضافة وتحويل منزلة. بالإضافة إلى استخدام طريقة حساب اللوغاريتم ثنائي لـ lb(x) والتي تقوم على الاستدعاء الذاتي لمربع x وتكرار العملية والاستفادة من ذلك.

${\log }_2(x^2)=2{\log }_2(x).$

متسلسلة القوى

متسلسلة تايلور

المقالة الرئيسية: متسلسلة تايلور وماكلورين

من أجل $x\in ]0,2[$ ، عندها يمكن كتابة العلاقة:

$\ln (x)=\sum _{n=1}^{\mathrm{\infty }}(-1{)}^{n+1}(\frac{(x-1{)}^n}{n})=(x-1)-\frac{(x-1{)}^2}{2}+\frac{(x-1{)}^3}{3}-\frac{(x-1{)}^4}{4}+\cdots$

مثال إيجاد تقريب لـ $\ln (\frac{3}{2})$

$\ln (\frac{3}{2})\approx (\frac{3}{2}-1)-\frac{(\frac{3}{2}-1{)}^2}{2}+\frac{(\frac{3}{2}-1{)}^3}{3}-\frac{(\frac{3}{2}-1{)}^4}{4}+\frac{(\frac{3}{2}-1{)}^5}{5}\approx \frac{391}{960}\approx 0.40$

متسلسلات أخرى

باستعمال تحويلات أويلر على متسلسلة تايلور نحصل على المتفاوتة التالية:

من أجل كل عدد حقيقي $x$

$\ln (x)=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{n}(1-\frac{1}{x}{)}^n=(1-\frac{1}{x})+\frac{1}{2}(1-\frac{1}{x}{)}^2+\frac{1}{3}(1-\frac{1}{x}{)}^3+\dots$

خواص وقوانين اللوغاريتم الطبيعي

اللوغاريتم الطبيعي والتكامل

$\ln (x)=\underset{1}{\overset{x}{\int }}\frac{1}{t}dt$ حيث $x>0$ ومنه فإن $\ln (1)=\underset{1}{\overset{1}{\int }}\frac{1}{t}dt=0$

الدالة الأصلية للوغاريتم الطبيعي $\int \ln (x)=x\ln (x)-x+c$حيث $c$ عدد حقيقي

خصائص جبرية

إن من بين أهم خصائص دالة اللوغاريتم الطبيعي هي خاصية تحويل الجداء إلى مجموع.

• $\ln (\coprod _{i=1}^n{a}_i)=\sum _{i=1}^n\ln (a_i)$ حيث $a_1$ و $a_2$ و $a_3$ و ... و $a_i$ أعداد حقيقية موجبة قطعا.

تاريخ اللوغاريتمات

اللوغاريتمات قديماً

نشر عالم الرياضيات الاسكتلندي جون نايبير أول بحث وجدول للوغاريتمات عام 1614م. وقد اكتشف السويسري جوبست برجي اللوغاريتمات على نحو مستقل في نفس الوقت تقريبا. وفي أوائل القرن السابع عشر، قدم الإنجليزي هنري برجز للرقم الأساسي 10، وبدأ في وضع جدول به 14 خانة للوغاريتمات العشرية، ثم أكمل الهولندي أدريان فلاك العمل الذي بدأه برجز. وحوالي عام 1622م، وضع الإنجليزي إدموند جنتر، تصورًا لفكرة كتابة الأعداد على مستطيلات رفيعة وفقًا للوغاريتم الخاص بكلٍ منها، وضربها وقسمتها عن طريق انزلاق مستطيل على الآخر. وتمثل هذه الفكرة أساس المسطرة المنزلقة. استمر استخدام جداول برجز - فلاك حتى تم وضع جداول لوغاريتمات عادية بها 20 خانة في بريطانيا في الفترة من 1924 و حتى 1949م.

اللوغاريتمات حديثاً

أدى استخدام الحواسيب والحاسبات الإلكترونية إلى إلغاء الحاجة إلى استخدام اللوغاريتمات في العمليات الحسابية. ومع ذلك، فإن اللوغاريتمات لها أهميتها في الأغراض النظرية.

إستخدامات اللوغاريتمات

• الضرب، لضرب رقمين باستخدام اللوغاريتمات، ابحث عن اللوغاريتم الخاص بكل من الرقمين في الجدول، وإجمع هذين اللوغاريتمين للحصول على لوغاريتم حاصل ضرب هذين الرقمين، ثم ابحث عن الرقم الذي يكون لوغاريتمه هو لوغاريتم حاصل ضرب الرقمين، مستخدمًا الجدول مرة أخرى.
• القسمة، لقسمة رقم على آخر، ابحث عن اللوغاريتم الخاص بكلٍ من الرقمين في الجدول، واطرح لوغاريتم المقام من لوغاريتم البسط، ثم استخدم الجدول مرة أخرى لمعرفة الرقم الذي يكون اللوغاريتم الخاص به هو لوغاريتم حاصل عملية الطرح هذه. هذا الرقم هو حاصل القسمة المطلوب.
• رفع الرقم إلى قوة معينة، لكي ترفع رقمًا إلى قوة معينة، ابحث في الجدول عن لوغاريتم هذا الرقم وإضرب هذا اللوغاريتم في أُس القوة، ثم ابحث في الجدول عن الرقم الذي يكون اللوغاريتم الخاص به هو نفس لوغاريتم حاصل عملية الضرب هذه. هذا الرقم هو القوة المطلوبة للرقم الأول.
• إيجاد الجذر، لمعرفة جذر رقم ما، ابحث عن لوغاريتم الرقم في الجدول، وإقسم هذا الرقم على أُس الجذر، ثم استخدم الجدول مرة أخرى لمعرفة الرقم الذي يكون اللوغاريتم الخاص به مساويًا لحاصل عملية القسمة، ويكون هذا هو الجذر المطلوب للرقم.

أنواع اللوغاريتمات

تقسم اللوغاريتمات إلى خمس أقسام- بحسب أنواعها -:

• لوغاريتمات عادية: تستخدم كل الأعداد عدا العشرة والاثنين والعدد النيبيري والأعداد المركبة.
• لوغاريتمات ثنائية: تستخدم العدد 2.
• لوغاريتمات عشرية: تستخدم العدد 10.
• لوغاريتمات طبيعية: بحيث تستخدم الرقم 2.72 في هذه العملية وهو ما يسمى بالعدد النيبيري.
• لوغاريتمات مركبة: تستخدم الأعداد المركبة.

الأصل اللغوي

لوغاريتم هي كلمة إنجليزية أُخذت من اسم العالم العربي الخوارزمي. أما الأسس فهي كلمة ذات أصل عربي وهي متناسقة مع الأس والذي يعني وضع الأساس. فالتعبير x4 يعني x تُبنى وتُرفع 4 مرات أي تضرب 4 مرات في نفسها.

وقيل إن أصل كلمة لوغارتم Logarithm قد يكون من الكلمتين إغريقيتين لوغوس (Logos) والتي تعني نسبة وأريتموس (Arithmos) والتي تعني عدد.

طالع أيضاً

• الجبر
• العدد النيبيري
• الضرب
• القسمة
• الجمع
• الطرح
• لوغاريتم طبيعي