حركة دائرية

  ميّز عن حركة دورانية.

الحركة الدائرية.

الحركة الدائرية في الفيزياء هي حركة يتحرك الجسم فيها بمحاذاة محيط دائرة ثابتة القطر، وتكون الحركة بسرعة ثابتة مقدارًا ومتغيرة اتجاهًا. التسارع المركزي: هو تسارع الجسم في الحركة الدائرية المنتظمة، ويكون اتجاهه دائما نحو المركز ولذلك يسمى بتسارع مركزي.

تتضمن الأمثلة عن الحركة الدائرية:

• قمر اصطناعي يدور حول الأرض على ارتفاع ثابت.
• جسم مربوط في خيط، ويتأرجح في دوائر.
• سيارة تدور حول منحنى في حلبة سباق.
• كهيرب يتحرك عموديًا على حقل مغناطيسي.
• ترس يدور داخل آلية .

أنواع الحركة الدائرية

رسم بياني للحركة الدائرية.

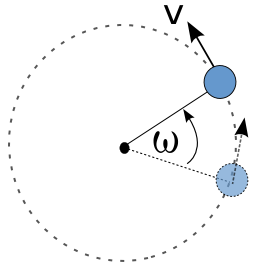
تعرف الحركة الدائرية بأنها حركة جسم على محيط دائرة وتكون على نوعين إما منتظمة أو غير منتظمة.

الحركة الدائرية المنتظمة

تحصل هذه الحركة عندما يقطع الجسم أقواس متساوية خلال فواصل زمنية متساوية ويتحقق ذلك إذا كان نصف قطر الدوران ثابت والانطلاق ثابت. ويكون للجسم تعجيل مركزي فقط.

الحركة الدائرية غير المنتظمة

تحصل هذه الحركة عندما يقطع الجسم أقواس غير متساوية في أزمان متساوية، ويتحقق ذلك إذا كان نصف قطر الدوران غير ثابت أو الانطلاق غير ثابت أو أن يكون كليهما غير ثابت. ويكون للجسم تعجيل مركزي وتعجيل مماسي.

• ملاحظة: المماس للدائرة عند أي نقطة يمثل اتجاه السرعة في هذة النقطة.

مفاهيم في الحركة الدائرية

التسارع المركزي

هو المعدل الزمني لتغير اتجاه الحركة، أي أن التعجيل المركزي ينشأ بسبب تغيير اتجاه الحركة دون الاعتماد على مقدارها، ويُحسب من العلاقة:

ت = ع^2 \ نق

حيث:

• (ت) التسارع المركزي ويقاس بوحدات (م\ث²).
• (ع) سرعة الجسم ويقاس بوحدات (م\ث).
• (نق) نصف قطر الدوران ويقاس بوحدات (م).

ومن مميزات هذا التعجيل أنه:

• ثابت المقدار ومتغير الاتجاه إذا كانت الحركة الدائرية منتظمة.
• متغير المقدار والاتجاه إذا كانت الحركة الدائرية غير منتظمة.

وفي كلتا الحالتين يتجه التعجيل نحو مركز الدوران، لذا سُمي بالتعجيل المركزي. ويُلاحظ أن التعجيل المركزي يعتمد على عاملين هما:

• مربع سرعة الانطلاق.
• ونصف قطر الدوران.

القوة المركزية

القوة المركزية هي القوة اللازمة لتغيير اتجاه الحركة بشكل مستمر والتي تحافظ على دوران الجسم في مساره الدائري، وتحسب من العلاقة التالية:

قم = ك س²\ نق ، وتقاس بوحدة النيوتن.

يمكن كتابة العلاقة السابقة بالشكل التالي قم = ك جم ، حيث (ك) تمثل كتلة الجسم وتقاس بوحدات الكتلة (كغم). وتمتاز هذه القوة بما يلي:

1. تخضع لقانون نيوتن الثاني في الحركة.
2. لايمكن لها أن تنجز شغل لعدم توفر الإزاحة باتجاه المركز.
3. قوة محصلة وليست معادلة (غير متزنة).
4. الجسم الذي يخضع لها يكون غير متزن.
5. تكون مساوية لقوة القصور الذاتي والتي تمنع الجسم من الحركة باتجاه مركز الدوران.
6. يكون اتجاهها دائما باتجاه مركز الدوران (أي بنفس الاتجاه مع التعجيل المركزي).
7. يعتمد مقدارها على مربع الانطلاق وكتلة الجسم ونصف قطر الدوران.
8. لايمكن أن تكون صفر لأن الجسم في هذه الحالة يتحرك باتجاه المماس لحظة الكف عن التأثير وتكون حركتة خطية.
9. يكون مقدارها ثابتًا إذا كانت الحركة الدائرية منتظمة، ومتغيرًا إذا كانت الحركة غير منتظمة وفي كلتا الحالتين يكون الاتجاه متغير ولكنها تتجه نحو مركز الدائرة لذا سميت بالقوة المركزية.

• ملاحظة: وجود القوة المركزية هو تطبيق لقانون نيوتن الأول في الحركة لأنها تعمل على تغيير حالة الجسم.

قوة القصور الذاتي

قوة القصور الذاتي هي قوة مساوية للقوة المركزية بالمقدار ومعاكسة لها بالاتجاه وتؤثر على جسم يختلف عن الجسم الذي تؤثر عليه القوة المركزية. فهي تطبيق لقانون نيوتن الثالث في الحركة (الفعل ورد الفعل) وتعتمد على كتلة الجسم ومربع انطلاق الجسم ونصف قطر الدوران، وتكون مسؤولة عن عدم السماح للجسم بالتحرك باتجاه مركز الدوران، كما أنها تساوي القوة المركزية مقدارًا وتعاكسها اتجاهًا كما هو مذكور أعلاه.

كيفية حل المسائل المتعلقة بالحركة الدائرية

1. نرسم الجسم ونُبين القوى المؤثرة عليه أولا ثم نأخذ القوى التي تتجه نحو مركز الدوران دائمًا كقوة مركزية.
2. إذا كانت هذه القوى مائلة نُحللها إلى مركباتها وناخذ المركبة التي تتجه نحو مركز الدوران كقوة مركزية.
3. إذا كانت تؤثر على الجسم أكثر من قوة نحو مركز الدوران فنوجد المحصلة لهذة القوى (نجمع القوى التي هي باتجاه واحد، ونطرحهم لو كانوا باتجاهين متعاكسين)
4. نساوي القوة أو محصلة القوة إلى الحد (ك س²\نق) ونجد ما هو مطلوب من السؤال.
5. يُمكن الاستفادة من القوى التي تكون على المحور العمودي لايجاد بعض المجاهيل التي نحتاج اليها في الحل.

صور مختلفة للقوة المركزية

القوة المركزية قد تكون كالآتي:

• إما أن تكون قوة شد كما في الخيط أو الوتر أو السلك المربوط به كرة تدور بدائرة افقية.
• أو أن تكون قوة احتكاك كما في المنعطفات الأفقية.
• أو تكون قوة رد فعل كما في سكة القطار وجهاز التسلية الدوار.
• أو مركبة قوة الشد الافقية كما في الرقاص المخروطي.
• أو المركبة الأفقية لرد الفعل كما في المنعطفات الافقية المائلة.
• أو محصلة وزن ورد فعل كما في الجسور والمنحدرات.
• أو محصلة وزن وشد كما في الكرة المربوطة بخيط وتدور بدائرة عمودية.

صيغ مشتقة

هناك صيغ مشتقة يمكن استعمالها مباشرة للحل وهي:

• مـ = س² \ نق ج ، مع المنعطفات الافقية.
• ظا هـ = س² \ نق ج ، مع كل المنعطفات المائلة بما فيها الدراجة والطائرة والرقاص المخروطي
• مـ = نق ج \ س² ، مع جهاز التسلية الدوار.

من التطبيقات الرياضية على الحركة الدائرية المنتظمة

كرة مربوطة بخيط تدور بدائرة أفقية، عربة على مسار دائري أفقي ومسار مائل، السكة الحديد، الجهاز الدوار، الدراجة، الطائرة، الرقاص المخروطي، دولاب الهواء.

من التطبيقات الرياضية على الحركة الدائرية غير المنتظمة

الجسور، المنحدرات، سكة الألعاب المسلية، كرة مربوطة بخيط تدور بدائرة عمودية.

انظر أيضًا

• حركة دورانية
• زخم زاوي
• معادلة حركة
• قوة وهمية
• حركة ترددية
• المدار الجغرافي الثابت
• مدار أرضي جغرافي متزامن
• رقاص (رياضيات)
• المدار الجغرافي الثابت
• حركة توافقية بسيطة
• القاذفة (سلاح)