تمثيل المعاوقة

جيمس كليرك ماكسويل أول مَنْ قام بربط القوة الميكانيكية بفرق الجهد الكهربي عام 1873.

تمثيل المعاوقة أو تمثيل ماكسويل، (بالإنجليزية: Impedance analogy)‏ هو أحد التمثيلات الكهربية الميكانيكية الأكثر شيوعًا، وسُمى بذلك لأنه يحافظ على التماثل بين المعاوقة الكهربية والمعاوقة الميكانيكية، على عكس تمثيل القبولية. استخدم جيمس كليرك ماكسويل التمثيل الميكانيكي لشرح أفكاره عن المجالات الكهرومغناطيسية، فكان أول مَنْ قام بربط القوة الميكانيكية بفرق الجهد الكهربي عام 1873م وبالتالي فيرجع له وضع بذرة تمثيل المعاوقة، وهو أول التمثيلات الكهربية الميكانيكية ظهورًا، بالرغم من أن مصطلح المعاوقة لم يكن قد صيغ بعد حتى صاغه أوليفر هيفسايد سنة 1886م، ثم طُوّرتْ الفكرة وقام آرثر كينيلي بتقديم فكرة المعاوقة المُعقدة سنة 1893م، ثم امتدّ مفهوم المعاوقة إلى المجال الميكانيكي سنة 1920م بواسطة آرثر كينيلي وآرثر جوردون ويبستر.

يُستخدَم تمثيل الأنظمة الميكانيكية على شكل دوائر كهربائية للاستفادة من التطورات النظرية الهائلة في تحليل الأنظمة الكهربائية المُعقدة، وخاصةً في مجال المرشحات. بتحويل النظام الميكانيكي إلى صيغة كهربائية يمكن تطبيق قواعد هندسة الدوائر الكهربية مباشرةً على النظام الميكانيكي دون تعديل، بالإضافة إلى أهمية استخدام التمثيل الكهربي الميكانيكي في الأنظمة الكهروميكانيكية؛ عن طريق تحويل الجزء الميكانيكي من النظام إلى صيغة كهربائية وبذلك يمكن إجراء تحليل واحد للنظام بأكمله.

عند تطبيق هذه الطريقة يكون السلوك الرياضي للنظام الكهربي المُحاكى مطابقًا للنظام الميكانيكي المُمثَّل، وكل عنصر في المجال الكهربي لديه عنصر مقابل في المجال الميكانيكي، وبالتالي جميع قوانين تحليل الدوائر الكهربية - مثل قوانين كيرشوف التي تُطبَّق في المجال الكهربي - يمكن تطبيقها أيضًا على النظام الميكانيكي المُمثَّل.

التطبيقات

يستخدم تمثيل المعاوقة على نطاق واسع لوضع نموذج لسلوك المرشحات الميكانيكية، حيث إنّ هذه المرشحات مصممة لاستخدامها في الدوائر الإلكترونية، لكنها تعمل بالكامل بطريقة ميكانيكية، وتستخدم المبدلات عند مداخل ومخارج المُرشحات للتحويل بين المجالين الكهربي والميكانيكي.

ومن التطبيقات الأخرى الشائعة، استخدامه في مجال المعدات السمعية مثل مكبرات الصوت، حيث تتكون مكبرات الصوت  من مبدلات وأجزاء ميكانيكية متحركة، كما أن الموجات الصوتية هي نفسها موجات ميكانيكية من تذبذبات جزيئات الموائع، ومن التطبيقات المُبكرة في هذا المجال؛ إجراء تحسينات كبيرة على الأداء الصوتي للفونوغراف. في عام 1929 صمم إدوارد نورتون مرشحًا ميكانيكيًا للفونوغراف، وتوقع من خلال التمثيل الكهربي لهذا المُرشح أن سلوكه سيكون مثل سلوك مُشرحات باتيرورث الإلكترونية.

العناصر

قبل البدء بعملية التمثيل الكهربي للنظام الميكانيكي؛ يجب وصف الشبكة الميكانيكية، بمجموعة من العناصر المثالية، ثم يتم استبدال كل عنصر بالعنصر الكهربي المناظر له.

يتم التمثيل حسب نموذج العناصر المُجمع، حيث نفترض أن العنصر الميكانيكي الذي تتم عليه العملية صغير جدًا لدرجة أن الزمن الذي تستغرقه الموجات الميكانيكية للمرور بين طرفيه يمكن إهمالها. يمكن أيضًا إجراء التمثيل حسب نموذج العناصر المُوزع مثلما يُطيق في تحليل خطوط النقل؛ لكن مميزات نموذج العناصر المُجمع أكبر. تُمثل العناصر الميكانيكية المُجمعة بثلاثة عناصر كهربية رئيسية هي المقاومة، والحث، والسعة، ويُختار «متغير جهد» ليتم تمثيله بفرق الجهد الكهربي، و«متغير تدفق» ليتم تمثيله بالتيار الكهربي. في تمثيل المعاوقة متغير الجهد هو القوة ومتغير التدفق هو السرعة. وبذلك يحافظ تمثيل المعاوقة على أن النسبة بين متغير الجهد ومتغير التدفق تساوي المعاوقة في كلا المجالين.

المقاومة

رمز المقاومة الكهربية على اليمين، والرمز الميكانيكي للمقاومة الميكانيكية (المُثبّط) على اليسار).

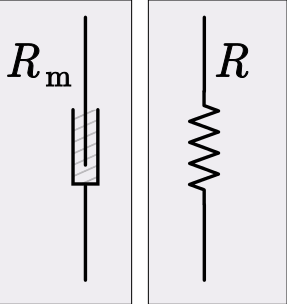
يُمثل "فقدان الطاقة في النظام الميكانيكي نتيجة عمليات مثل الاحتكاك" بـ"المقاومة الكهربية"، المكون الميكانيكي المماثل الذي يمكن تمثيله بالمقاومة هو ممتص الصدمات أو الذي يؤدي وظيفة التخميد. القانون الذي يوضح العلاقة بين المقاومة الكهربية والصيغ الفيزيائية الأخرى هو قانون أوم:

$v=iR$

والمعادلة المماثلة في المجال الميكانيكي:

$F=u{R}_{\mathrm{m}}$

حيث: R هي المقاومة الكهربية، وv هو فرق الجهد، وi هو التيار الكهربي، وR_m هي المقاومة الميكانيكية، أو التخميد، وF هي القوة، وu هي السرعة الناجمة عن القوة.

المقاومة الكهربية تمثل الجزء الحقيقي من المعاوقة الكهربية، وكذلك المقاومة الميكانيكية.

الحث

رمز المحث أو الملف الكهربي على اليمين، ومماثله في النظام الميكانيكي رمز الكتلة على اليسار.

الكمية الميكانيكية التي يتم تمثيلها بـ"الحث" في تمثيل المعاوقة هي "الكتلة". واعتُمِدَ في ذلك على أن الكتلة تعتبر مخزن للطاقة كما يُخرن الملف التيار الكهربي، ويخضع للمعادلة: 

$v=L\frac{di}{dt}$

والمعادلة المماثلة في المجال الميكانيكي هي قانون نيوتن الثاني للحركة:

$F=M\frac{du}{dt}$

حيث: L هو الحث، وt هو الزمن، وM هي الكتلة.

معاوقة المحث هي قيمة خيالية يُعبر عنها بالمعادلة:

$Z=j\omega L$

والمعادلة المماثلة في المجال الميكانيكي:

$Z_{\mathrm{m}}=j\omega M$

حيث: Z هي المعاوقة الكهربائية، وj هو الوحدة التخيلية حيث j² = −1، وω هو التردد الزاوي، وZ_m هي المعاوقة الميكانيكية.

السعة

رمز السعة الكهربية الممثلة بالمُكثف على اليمين، ورمز الجساءة (بالإنجليزية: Stiffness) التي يُمكن تمثيلها بالزُنْبُرُك أو السوستة.

الكمية الميكانيكية التي يتم تمثيلها بـ«السعة» هي المطاوعة وهي مقلوب الجساءة (بالإنجليزية: Stiffness)‏، أما التمثيل الكهربي هو المرانة معكوس السعة وهو أقل استخدامًا. وعلى ذلك يمكن تمثيل المكثف في المجال الكهربي بالنابض أو الزُنْبُرُك في المجال الميكانيكي. تخضع السعة الكهربية للمعادلة:

$v=D\int idt$

والمعادلة المماثلة في المجال الميكانيكي هي قانون هوك:

$F=S\int udt$

حيث: D هو المرانة ويساوي مقلوب السعة (1/C)، وC هو السعة، وS هو الجساءة.

معاوقة المكثف هي قيمة خيالية يُعبر عنها بالمعادلة:

$Z=\frac{D}{j\omega }$

والمعادلة المماثلة في المجال الميكانيكي:

$Z_{\mathrm{m}}=\frac{S}{j\omega }$

وأيضًا يُمكن كتابتها على الشكل التالي:

$Z_{\mathrm{m}}=\frac{1}{j\omega C_{\mathrm{m}}}$

حيث: C_m = 1/S هي المطاوعة الميكانيكية، والتي يُمكن مماثلتها مباشرة مع السعة الكهربية.

الرنَّان

يُمثل الرنان الميكانيكي بكتلة M ومطاوعة C_m في المجال الميكانيكي، ويُمثل في المجال الكهربي بدائرة رنان محث L ومكثف C تتكون من الحث والسعة. إذا كان لدينا كتلة ومطاوعة مثاليتين فسوف تكوّنان رنّانًا ميكانيكيًا مثلما يحدث في المجال الكهربي مع المحث والمكثف المثاليين، لكن في الواقع من الصعب الحصول على قيمة مثالية لأي من المكونات سواء الميكانيكية أو الكهربية، فلا يوجد مكثف محض ولا مطاوعة محضة، فالنابض مثلا يحتوي على مطاوعة وعلى كتلة صغيرة، والكتلة تحتوي بالأساس على كتلة وعلى مطاوعة صغيرة، ولكن يتم نظريًا فرض وجود مكونات مثالية لنتمكن من تمثيلها وتحليلها. الرنان الميكانيكي هو أهم مكون للمرشحات الميكانيكية.

المُولِّدات

رمز مصدر الجهد الكهربي الثابت على اليمين، ويُمثل في المجال الميكانيكي بالقوة الميكانيكية الثابتة على اليسار.

رمز مصدر التيار الكهربي الثابت على اليمين، ويُمثل في المجال الميكانيكي بالسرعة الثابتة على اليسار.

يتم تمثيل مصدر الجهد الكهربي الثابت V في تمثيل المعاوقة بمصدر القوة الميكانيكية الثابتة F، فمصدر الجهد الكهربي بمثابة القوة التي تدفع التيار الكهربي في المجال الكهربي، أما مصدر التيار الكهربي الثابت i فيتم تمثيله بمصدر السرعة الثابتة، حيث يعتمد تمثيل المعاوقة على مقدار التشابه في أن التيار الكهربي يُعبّر عن سرعة تدفق الشحنات الكهربية.

من الأمثلة العملية على مصادر القوة الميكانيكية الثابتة النابض ثابت القوة (بالإنجليزية: constant-force spring)‏، وهو يماثل مصدر الجهد الكهربي المثالي، مثل بطارية كهربية تظل تعطي جهدًا ثابتًا لحمل أكبر بكثير من مقاومتها الداخلية، ومن الأمثلة العملية على مصدر السرعة الثابتة الآلات ذات الحمل الحفيف، مثل محرك كهربي، يقود سير في مصنع.

محولات الطاقة

تتطلب الأنظمة الكهروميكانيكية استخدام المبدلات أو محولات الطاقة للتحويل بين المجالين الكهربي والميكانيكي، حيث تستخدم أسلوب الشبكات ثنائية المنفذ (بالإنجليزية: two-port networks)‏، وتُوصف هؤلاء بمعادلتين وأربع متغيرات مجهولة يمكن كتابتها على شكل مصفوفة ثنائية، ويُعبَّر عن قيمة المجاهيل الأربعة بوحدة المعاوقة: 

$\left[\begin{array}{c}v\\ F\end{array}\right]=\left[\begin{array}{cc}{z}_{11}& z_{12}\\ z_{21}& z_{22}\end{array}\right]\left[\begin{array}{c}i\\ u\end{array}\right]$

على سبيل المثال: المتغير $z_{22}$ يعبر عن المعاوقة الميكانيكية للدائرة المفتوحة من الجانب الميكانيكي لمحول الطاقة في حالة عدم مرور تيار كهربي (دائرة مفتوحة) من الجانب الكهربي. والعكس مع المتغير $z_{11}$ حيث يعبر عن المعاوقة من الجانب الكهربي عندما يكون الجانب الميكانيكي ساكنًا (السرعة بصفر)، أما المتغيران الآخران $z_{21}$ و$z_{12}$ فيعبران عن معاوقة النقل من الاتجاهين الأمامي والعكسي.

المحولات

يمكن تمثيل المحول الكهربي بآلة ميكانيكية بسيطة مثل البكرة أو الرافعة، القوة الواقعة على الحمل قد تكون أكبر أو أصغر من القوة الداخلة اعتمادًا على ما يُسمى بالميزة الميكانيكية، إن كانت قيتمها أكبر أو أصغر من الواحد. تماثل الميزة الميكانيكية في تمثيل القبولية بالنسبة بين عدد لفات طرفي المحول، فإن كانت الميزة الميكانيكية للآلة أكبر تُمثَّل بمحول رافع للجهد، وإن كانت أقل تُمثَّل بمُحول خافض للجهد.

معادلات القدرة والطاقة

الكهربائية الكمية	المعادلة الكهربية	التمثيل الميكانيكي	المعادلة الميكانيكية
الطاقة الموردة	$E=\int vidt$	الطاقة الموردة	$E=\int Fudt$
القدرة الموردة	$P=vi$	القدرة الموردة	$P=Fu$
القدرة المُبددة في المقاومة	$P=i^{2}R=\frac{v^2}{R}$	القدرة المُبددة في المُثبّط	$P=u^2{R}_{\mathrm{m}}=\frac{F^2}{R_{\mathrm{m}}}$
الطاقة المُخزَّنة في المحث	$E=\frac{1}{2}L{i}^2$	الطاقة الحركية لتحريك كتلة	$E=\frac{1}{2}M{u}^2$
الطاقة المُخزَّنة في المكثف	$E=\frac{1}{2}C{v}^2$	طاقة الوضع المُخزَّنة في النابض	$E=\frac{1}{2}{C}_{\mathrm{m}}{F}^2$

أمثلة

دائرة رنين بسيطة

يوضح الشكل دائرة رنين ميكانيكية بسيطة مكونة من كتلة M موصلة على التوازي مع نباض S ومقاومة ميكانيكية R، وتُمثل باستخدام تمثيل المعاوقة بدائرة رنين مكونة من مقاومة ومحث ومكثف على التوالي.

دائرة رنين ميكانيكية بسيطة على اليسار، وتمثيلها الكهربي على اليمين.

نموذج الأذن البشرية

تشريح الأذن

يُمكن تمثيل الأذن البشرية على شكل دائرة كهربية باستخدام تمثيل المعاوقة، الشكل بالأسفل يوضح إحدى هذه التمثيلات، أقصى اليسار يُمثل قناة الأذن، ويليها محول يُمثِّل طبلة الأذن، حيث إنّ طبلة الأذن تحول الموجات الصوتية في الهواء في قناة الأذن إلى اهتزازات ميكانيكية في عظام الأذن الوسطى. أما في القوقعة يتم تغيير وسط الاهتزازات الميكانيكية من الهواء إلى السائل في القوقعة. يجمع هذا المثال على أربعة مجالات مختلفة ممثلة بدائرة كهربية واحدة: المجال الميكانيكي والصوتي وتدفق الموائع، بالإضافة إلى المجال الكهربي الممثل في النبضات العصبية التي تتدفق إلى الدماغ والتي ضُمِّنت في النموذج.

يستخدم جزء القوقعة في الدائرة طريقة تحليل العناصر المحدودة لخط النقل المستمر لقناة القوقعة، لبناء تمثيل مثالي للأذن البشرية يُستخدم عددًا لا حصر له من العناصر متناهية الصغر، فنموذج القوقعة وحده ينقسم إلى 350 قسم، كل قسم يستخدم عددًا لا حصر له من العناصر المجمعة.

واحدة من الدوائر التي تُمثل الأذن البشرية باستخدام تمثيل المعاوقة.

المزايا والعيوب

الميزة الرئيسية في تمثيل المعاوقة بالمقارنة بتمثيل القبولية هو أنه يحافظ على التماثل بين المعاوقة الكهربية والميكانيكية، فتُمثل المعاوقة الميكانيكية بالمعاوقة الكهربية في الدائرة المماثلة والعكس صحيح، كما أن تمثيل المعاوقة أكثر منطقية، فمن المنطقي تمثيل القوة بفرق الجهد الكهربي لما بينهما من تشابه، وأحيانًا يُسمى مصدر الجهد الكهربي بالقوة الدافعة الكهربية، وكذلك تمثيل السرعة بالتيار الكهربي أكثر منطقية، فالتيار الكهربي يُعبر عن سرعة تدفق الشحنات الكهربية، يقود ذلك إلى تماثل المعاوقة الكهربية والميكانيكية.

بينما أحد العيوب الرئيسية في تمثيل المعاوقة هو أنه لا يحافظ على طوبولوجيا النظام الميكانيكي، حيث إنّ العناصر الموصلة على التوالي في النظام الميكانيكي تُمثل بعناصر موصلة على التوازي في النظام الكهربي، والعكس بالعكس.

شيء آخر قد يُعتبر أحد العيوب، وهو أن مصفوفة المعاوقة الخاصة بمحولات الطاقة تُحول القوة في المجال الميكانيكي إلى التيار في المجال الكهربي، والسرعة في المجال الميكانيكي إلى فرق الجهد في المجال الكهربي، بالرغم أن القوة تُمثل بفرق الجهد وليس التيار، وهذا قد يبدو وكأنه عيب. ومع ذلك فإن العديد مِن استخدامات محولات الطاقة، خصوصًا في الترددات الصوتية، تعمل بواسطة الحث الكهرومغناطيسي والذي يحكمه علاقة مثل هذه، فعلى سبيل المثال فإن قانون لورنتس يعطى علاقة مباشرة بين القوة والتيار الكهربي:

$F=BIl$

حيث: B هي كثافة التدفق المغناطيسي، وl هو طول الموصل الكهربي.

التاريخ

يسمى تمثيل المعاوقة أحيانًا بـتمثيل ماكسويل، حيث استخدم جيمس كليرك ماكسويل (1831-1879) التمثيل الميكانيكي لشرح أفكاره عن المجالات الكهرومغناطيسية، فكان أول مَنْ قام بربط القوة الميكانيكية بفرق الجهد الكهربي عام 1873 وبالتالي فيرجع له وضع بذرة تمثيل المعاوقة، وهو أول التمثيلات الكهربية الميكانيكية ظهورًا، بالرغم من أن مصطلح المعاوقة لم يكن قد صيغ بعد حتى صاغه أوليفر هيفسايد سنة 1886، ثم طُوّرتْ الفكرة وقام آرثر كينيلي بتقديم فكرة المعاوقة المُعقدة سنة 1893، ثم امتدّ مفهوم المعاوقة إلى المجال الميكانيكي سنة 1920 بواسطة آرثر كينيلي وآرثر جوردون ويبستر.

وكان هنري بوانكاريه أول من وصف المُبدّل بمعادلات جبرية خطية تربط المتغيرات الكهربية (فرق الجهد والتيار) بالمتغيرات الميكانيكية المتغيرات (القوة والسرعة) وذلك في عام 1907. وفي عام 1921، قام ويغيل بالتعبير عنه بمعادلات بدلالة المعاوقة الميكانيكية كمماثلة للمعاوقة الكهربية.

قراءة مُوسّعة

1. Beranek & Mellow، Beranek, Leo Leroy; Mellow, Tim J. (2012). Acoustics: Sound Fields and Transducers. Academic Press. ISBN:0123914213.{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
2. Busch-Vishniac، Ilene J. (1999). Electromechanical Sensors and Actuators. Springer Science & Business Media. ISBN:038798495X.
3. Carr، Joseph J. (2002). RF Components and Circuits. Newnes. ISBN:0-7506-4844-9.
4. Eargle، John (2003). Loudspeaker Handbook. Kluwer Academic Publishers. ISBN:1402075847.
5. Jackson، Roger G. (2004). Novel Sensors and Sensing. CRC Press. ISBN:1420033808.
6. Kleiner، Mendel (2013). Electroacoustics. CRC Press. ISBN:1439836183.
7. Martinsen & Grimnes، Martinsen, Orjan G.; Grimnes, Sverre (2011). Bioimpedance and Bioelectricity Basics. Academic Press. ISBN:0080568807.{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
8. Pierce، Allan D. (1989). Acoustics: an Introduction to its Physical Principles and Applications. Acoustical Society of America. ISBN:0883186128.
9. Pipes & Harvill، Pipes, Louis A.; Harvill, Lawrence R. (2014). Applied Mathematics for Engineers and Physicists. Courier Dover Publications. ISBN:0486779513.{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
10. Talbot-Smith، Michael (2013). Audio Engineer's Reference Book. Taylor & Francis. ISBN:1136119736.
11. Taylor & Huang، Taylor, John; Huang, Qiuting (1997). CRC Handbook of Electrical Filters. CRC Press. ISBN:0849389518.{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
12. Paik، H. J. (1996). Superconduction accelerometers, gravitational-wave transducers, and gravity gradiometers, pp. 569–598, in Weinstock, Harold, SQUID Sensors: Fundamentals, Fabrication, and Applications. Springer Science & Business Media. ISBN:0792343506.
13. Eargle، John (1996). Superconduction accelerometers, gravitational-wave transducers, and gravity gradiometers, pp. 569–598, in Weinstock, Harold, SQUID Sensors: Fundamentals, Fabrication, and Applications. Springer Science & Business Media. ISBN:0792343506.
14. Poincaré، H. (1907). Study of telephonic reception, vol. 50, pp. 221–372. Eclairage Electrique.
15. Wegel، R. L. (1921). Theory of magneto-mechanical systems as applied to telephone receivers and similar structures, vol. 40, pp. 791–802. Journal of the American Institute of Electrical Engineers.
16. Darlington، S. (1984). A history of network synthesis and filter theory for circuits composed of resistors, inductors, and capacitors, vol. 31, no. 1, pp. 3–13. IEEE Transactions on Circuits and Systems. مؤرشف من الأصل في 2019-12-15.
17. Fukazawa & Tanaka، Fukazawa, Tatsuya; Tanaka, Yasuo (1993). Evoked otoacoustic emissions in a cochlear model, pp. 191–196 in Hohmann, D. (ed), ECoG, OAE and Intraoperative Monitoring: Proceedings of the First International Conference, Würzburg, Germany, September 20–24, 1992. Kugler Publications. ISBN:9062990975.{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
18. Harrison، Henry C. (1929). Acoustic device. U.S. Patent 1,730,425, filed 11 October 1927 (and in Germany 21 October 1923), issued 8 October 1929.
19. Hunt، Frederick V. (1954). Electroacoustics: the Analysis of Transduction, and its Historical Background. Harvard University Press. OCLC:2042530.
20. Stephens & Bate، Stephens, Raymond William Barrow; Bate, A. E (1966). Acoustics and vibrational physics. Edward Arnold. OCLC:912579.{{استشهاد بكتاب}}: صيانة الاستشهاد: أسماء متعددة: قائمة المؤلفين (link)
21. de Silva، Clarence W. (2006). Vibration: Fundamentals and Practice. CRC Press. ISBN:0849319870.