|
تضامنًا مع حق الشعب الفلسطيني |
اقتصار (رياضيات)
تحتاج هذه المقالة كاملةً أو أجزاءً منها إلى تدقيق لغوي أو نحوي. |
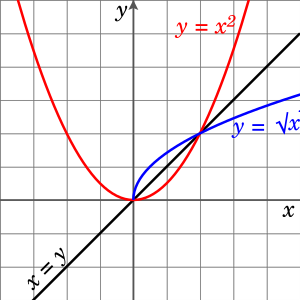
في الرياضيات، اقتصار دالة [1] هي دالة جديدة يرمز لها بـ أو ، يُحْصَلُ عليها من خلال اختيار أصغر مجال للدالة الأصلية .
تعريف
بفرض أن هي دالة من مجموعة لمجموعة ، وإذا كانت المجموعة هي مجموعة فرعية من ، فإن اقتصار على هي الدالة:[2]حيث لكل قيم ، بمعنى أن اقتصار على هي نفس الدالة ، ولكن معرفة فقط على .
إذا نظرنا للدالة على أنها علاقة رياضية في الجداء الديكارتي ، فإن اقتصار على يمكن تمثيله بالرسم البياني الخاص بها حيث العلاقة تمثل الأزواج المرتبة في الرسم البياني
امتدادات
يُقال أن دالة امتداد ( باللغة الأنجليزية "extension") دالة أخرى إذا كان في كل مرة تكون في مجال ، فإنها أيضا في مجال و . تحديدًا إذا كانت و
الامتداد الخطي (باللغة الأنجليزية "linear extension" وأيضًا الامتداد المستمر) للدالة هو تحويل خطي لـ (وأيضًا تحويل مستمر).
أمثلة
- اقتصار الدالة الغير متباينة على المجال هو التباين .
- دالة المضروب تنتج من اقتصار الدالة غاما على مجموعة الأعداد الصحيحة الموجبة لأننا نطرح 1 من ، أي: .
خصائص الاقتصار
- اقتصار دالة على المجال بأكمله يعيد إلى الدالة الأصلية، أي .
- اقتصار دالة مرتين هو نفسه اقتصارها مرة واحدة، أي إذا كان ، فإنّ: .
- اقتصار الدالة المحايدة المعرفة على مجموعة على مجموعة فرعية من هو مجرد تباين قانوني من إلى [3]
- اقتصار دالة مستمرة هو عبارة عن دالة مستمرة.[4][5]
تطبيقات
دوال عكسية
لكي يكون لـ الدالة دالة عكسية، يجب أن تكون تقابلية، وإذا لم تكن f كذلك، يمكن تحديد دالتها العكسية عن طريق اقتصارها (تقييدها) على جزء من المجال.
على سبيل المثال، دالة المُعرّفة عموماً على ليست تقابلية لأن وذلك لكل من
ومع ذلك، تصبح الدالة تقابلية إذا اقتصرنا على المجال ، في هذه الحالة
ملاحظة:
إذا كنا نود أن نقتصر على المجال ، فإن دالتها العكسية ستكون( ) بدلًا من ذلك، ليست هناك حاجة لاقتصار المجال إذا كنا لا نريد إيجاد الدالة العكسية كونها دالة متعددة القيم.
اختيار المؤثرات
هذا القسم فارغ أو غير مكتمل. ساهم في توسيعه. |
الحزم
هذا القسم فارغ أو غير مكتمل. ساهم في توسيعه. |
انظر أيضاً
مراجع
- ^ ترجمة و معنى restriction في قاموس المعاني. قاموس عربي انجليزي نسخة محفوظة 3 يناير 2020 على موقع واي باك مشين.
- ^ Stoll، Robert (1974). Sets, Logic and Axiomatic Theories (ط. 2nd). San Francisco: W. H. Freeman and Company. ص. [36]. ISBN:0-7167-0457-9.
- ^ Halmos، Paul (1960). Naive Set Theory . Princeton, NJ: D. Van Nostrand. Reprinted by Springer-Verlag, New York, 1974. (ردمك 0-387-90092-6) (Springer-Verlag edition). Reprinted by Martino Fine Books, 2011. (ردمك 978-1-61427-131-4) (Paperback edition).
- ^ Munkres، James R. (2000). Topology (ط. 2nd). Upper Saddle River: Prentice Hall. ISBN:0-13-181629-2.
- ^ Adams، Colin Conrad؛ Franzosa، Robert David (2008). Introduction to Topology: Pure and Applied. Pearson Prentice Hall. ISBN:978-0-13-184869-6.