متجه برغر

في علم المواد، متجه برجر، الذي سمي على اسم الفيزيائي الهولندي يان برجرز، هو متجه، غالبًا ما يُشار إليه بالرمز b، ويمثل حجم واتجاه التشوه البلوري الناتج عن إنحراف في الشبكة البلورية.

متجه برغر في إنحراف الحافة (يسار) وفي إنحراف دوراني (يمين). يمكن تخيل إنحراف الحواف على أنه إدخال نصف مستوى (مربعات رمادية) لا يتناسب مع التناظر البلوري. يمكن تخيل إنحراف الدوران كعملية قطع وتمزيق على امتداد نصف مستوى.

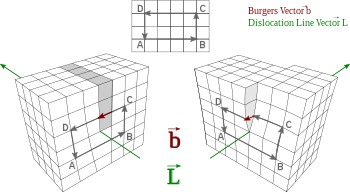
يتم فهم حجم المتجه واتجاهه بشكل أفضل عندما يتم تصور الهيكل البلوري الحامل للخلع(أو الإنحراف) لأول مرة دون الخلع، أي الهيكل البلوري المثالي. في هذا الهيكل البلوري المثالي، يتم رسم مستطيل تكون أطواله وعرضه مضاعفات صحيحة لـ "a" (طول حافة البنية البلورية ) يشمل موقع أصل الخلع الأصلي. بمجرد رسم هذا المستطيل الشامل، يمكن إدخال الخلع. سيكون لهذا الخلع تأثير تشوه، ليس فقط على البنية البلورية المثالية، ولكن على المستطيل أيضًا. يمكن أن يكون المستطيل المذكور منفصلاً عن الجانب العمودي، مما يؤدي إلى قطع اتصال الطول والعرض لأجزاء المستطيل عند أحد زوايا المستطيل، وإزاحة كل قطعة مستقيمة عن بعضها البعض. ما كان في السابق مستطيلًا قبل إدخال الخلع أصبح الآن شكلًا هندسيًا مفتوحًا يحدد فتحه اتجاه وحجم متجه برجر. على وجه التحديد، يحدد عرض الفتح حجم متجه برجر، وعند إدخال مجموعة من الإحداثيات الثابتة، يمكن تحديد زاوية بين نهاية مقطع خط طول المستطيل المخلوع وقطعة خط العرض.

عند حساب متجه برجر عمليًا، يمكن للمرء رسم دورة مستطيلة عكس اتجاه عقارب الساعة من نقطة البداية لإحاطة التفكك (انظر الصورة أعلاه). سيكون متجه برجر هو المتجه لإكمال الدائرة، أي من نهاية الدائرة إلى بداية الدائرة.

يعتمد اتجاه المتجه على مستوى التفكك، والذي يكون عادةً على أحد أقرب مستويات التصوير البلوري. عادةً ما يتم تمثيل الحجم بواسطة المعادلة (لبنية BCC و FCC فقط):

$\left|\mathbf{b}\right|=(a/2)\sqrt{h^2+k^2+l^2}$

حيث a هو طول حافة خلية البنية البلورية، || b || هو حجم متجه برجر و h و k و l هي إحداثيات متجه برجر، b = $(a/2)⟨hkl⟩$، ويعزى المعامل a / 2 إلى حقيقة أنه في بنيتي BCC و FCC، يمكن التعبير عن أقصر المتجهات الشبكية كالتالي $(a/2)⟨hkl⟩$ . نسبيًا، بالنسبة للبنية المكعبة البسيطة، b = $a⟨hkl⟩$ وبالتالي يتم تمثيل الحجم بواسطة

$\left|\mathbf{b}\right|=a\sqrt{h^2+k^2+l^2}$

في معظم المواد الفلزية، يكون حجم متجه برجر للإنحراف مساوياً للتباعد بين الذرات للمادة، نظرًا لأن الخلع الفردي سيعوض الشبكة البلورية بوحدة تباعد بلورية واحدة مكتظة.

في حالات إنحراف الحواف، يكون خط العيب البلوري ومتجه البرغر متعامدين مع بعضهما البعض. أما في إنحراف الدوران، فهي متوازية.

يعتبر متجه برجر مهمًا في تحديد مقاومة الخضوع للمادة من خلال التأثير على التصلب المذاب، وتصلب الترسيب والتصلب أثناء الشغل . يلعب متجه برجر دورًا مهمًا في تحديد اتجاه خط الخلع.