|
تضامنًا مع حق الشعب الفلسطيني |
قانون جيب التمام
قانون جيب التمام |
| جزء من سلسلة مقالات حول |
| حساب المثلثات |
|---|
 |
| بوابة رياضيات |

قانون جيب التمام أو قانون التجيب أو مبرهنة الكاشي هي مبرهنة في هندسة المثلثات[ملاحظة 1] تربط ضلع أي مثلث بضلعيه الآخرين وجيب تمام الزاوية المحصورة بينهما. ينص قانون جيب التمام على أنه في أي مثلث أطوال أضلاعه a, b, c المقابلة للزوايا α, β, γ فإنَّ:[1]
.
قانون جيب التمام يُعمم نظرية فيثاغورس لأي مثلث بأي زوايا. بوضع نجد أنَّ ومنها نظرية فيثاغورس .
التسمية
سُميت بهذا الاسم نسبة إلى العالم غياث الدين الكاشي الذي نشر هذه المبرهنة في كتابه «مفتاح الحساب» عام 1429 م.
التاريخ
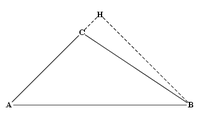
في كتاب العناصر لإقليدس، نجد مقاربة هندسية لتعميم مبرهنة فيثاغورس: نجد في الكتاب 2 العبارتين 12 و13, حيث يتم التطرق لحالة مثلث عادي بزاوية منفرجة وفي مثلث عادي بزوايا حادة. لكن عدم وجود الدوال المثلثية (آنذاك) وكذلك الجبر أدى إلى استعمال المساحات.
فالعبارة 12 :
وفي الشكل المقابل المثلث ABC مثلث منفرج الزاوية في C والقطعة المستقيمة CH هي مسقط الضلع BC على الضلع AC (انظر شكل2) وبالتالي وطبقاً للنظرية يكون
و كان يجب انتظار العرب المسلمين لتظهر الدوال المثلثية لرؤية المبرهنة في تطورها: فالفلكي والرياضي البتاني عمم نتيجة إقليدس في الهندسة الفضائية والتي مكنت من القيام بحساب المسافات بين النجوم. وفي نفس الوقت تم إنشاء جداول للدوال المثلثية والتي أتاحت للعالم غياث الدين الكاشي صياغة المبرهنة في شكلها النهائي.
تطبيقات
مبرهنة الكاشي في تعميم لمبرهنة فيتاغورس، عندما تكون الزاوية : قائمة، أو عندما يكون: ، المبرهنة تصبح:, و عكسيا.

النظرية تستعمل في المثلثات(انظر شكل. 3)حل مثلث، أي تحديد:
- الضلع الثالث لمثلث نعرف فيه زاوية والضلعين المكونين لها:
- ;
- زوايا مثلث نعرف فيه الأضلاع:
- .
البراهين
بتقسيم المساحات
من بين طرق البرهنة حساب المساحات، حيث يتم ملاحظة ما يلي:
- , و هي مساحات لمربع أضلاعه على التوالي , و
- وهو ل متوازي أضلاع من جهة و يكونان زاوية ، تغيير إشارة: تصبح الزاوية منفرجة تجعل دراسة الحالات ضرورية.

الشكل 4أ (جانبه) يقسم سباعي بكيفيتين مختلفتين حيث تتم البرهنة في حالة زاوية حادة. يدخل هنا :
- بالوردي، lالمساحات , في اليسار، والمساحات و في اليمين ;
- بالأزرق، المثلث ABC، في اليمين كما في اليسار ;
- بالرمادي، بعض المثلثات الإضافية، متطابقة مع المثلث ABC وبنفس العدد في التقسيمين.
تساوي المساحات في اليمين واليسار يعطي
- .

الشكل 4ب (جانبه) يقسم سداسي بكيفيتين مختلفتين بكيفية برهن في حالة زاوية منفرجة. الشكل يبين
- بالوردي، المساحات , و في اليسار، والمساحات في اليمين ;
- بالأزرق، مرتين المثلث ABC، في اليمين كما في اليسار.
تساوي المساحتين يمينا ويسارا يعطي
- .
باستعمال نظرية فيتاغورس
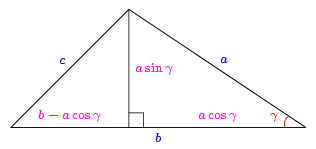
الشكل 5 (جانبه) يبين طريقة البرهنة باستعمال مبرهنة فيتاغورس في مثلث قائم الزاوية ناتج عن طريق الارتفاع :
بنفس الطريقة نبرهن في حالة مثلث بزاوية منفرجة.
في الهندسة اللاإقليدية
في الهندسة الكروية
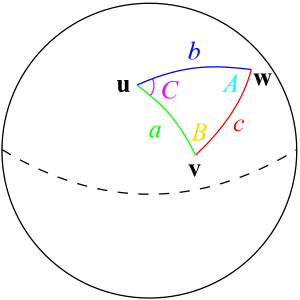
توجد نسخ مشابهة لقانون جيب التمام للمثلثات المستوية أيضًا في كرة الوحدة (نصف قطرها يساوي 1) وفي المستوي الزائدي. في الهندسة الكروية، يعرّف المثلث بثلاث نقاط u وv، و w على كرة الوحدة، وأقواس الدوائر العظمى التي تربط تلك النقاط. إذا كانت هذه الدوائر العظمى تصنع الزوايا A، B، و C مع الأضلاع المقابة a، b، c فإن القانون الكروي لجيب التمام ينص أن:
في الهندسة الزائدية
في الهندسة الزائدية، تُعرف المعادلتين معًا باسم قانون جيب التمام للمثلثات الزائدية. الأولى هي:
حيث sinh و cosh هي دالتي الجيب وجيب التمام الزائديتان.
والثانية هي:
كما هو الحال في الهندسة الإقليدية ، يمكن للمرء استخدام قانون جيب التمام لتحديد الزوايا A, B, C من معرفة الأضلاع a، b، c. على عكس الهندسة الإقليدية، فإن العكس ممكن أيضًا في كلا المثلثين اللاإقليديين: تحدد الزوايا A، B، C الأضلاع a، b، c.
انظر أيضًا
ملاحظات
- ^ هي أيضاً تعميم لمبرهنة فيثاغورس على أي زاوية من زوايا المثلث (ليست بالضرورة قائمة).
| في كومنز صور وملفات عن: قانون جيب التمام |
مراجع
- ^ Java applet version by Prof. D E Joyce of Clark University. نسخة محفوظة 05 أغسطس 2017 على موقع واي باك مشين.
