مبرهنة نايكويست وشانون

مثال على رفع تردد الموجة مع بقاء تردد الإعتيان ثابت. نلاحظ في البداية نظراً لتحقق شرط نظرية شعنون استخراجا صحيحا للإشارة: $f_{sampling}>2\cdot f_{max}$، لكن فيما بعد وبسبب جرح هذا الشرط تكون الإشارة المُسترجعة (الخط المنفصل) غير مطابقة لتلك الأصلية.

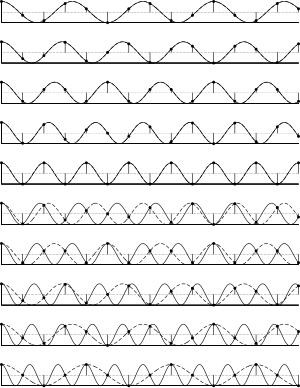
مبرهنة شانون ونايكويست أو مبرهنة شانون ونايكويست في الاستعيان (بالإنجليزية: Nyquist–Shannon sampling theorem)‏ هي من أهم المبرهنات في التقنيات الرقمية الحديثة والعلوم المتصلة بها مثل المعالجة الرقمية للإشارة والمعلوماتية ونظرية المعلومات.

تعود المبرهنة إلى جهد العالمين كلود شانون وهاري نايكست. وممن اشتهر في هذه المبرهنة العالم العراقي الأمريكي عبدالجبار جري.

الإشكال الذي تعالجه المبرهنة

لنعتبر أنه لدينا إشارة متواترة أي غير متقطعة, بغض النظر عن طبيعة هذه الإشارة سواء أن كانت تيارا كهربائيا أو غيره, وإذا قمنا بتحويل هذه الإشارة المتواصلة المتواترة إلى إشارة غير متواترة أي متقطعة كما هو الحال في العديد من التقنيات الرقمية, فإن ذلك يتم عن طريق أخذ عينات من الإشارة.

مجموعة العينات هذه تكون المقابل الرقمي للإشارة المتواترة. السؤال المطروح هو: ما العدد المناسب من العينات التي يجب أن نأخذها حتى يتسنى لنا لاحقا انطلاقا من هذه العينات إعادة تركيب الإشارة الأصلية أو إيجادها. أو بلغة أخرى ما هو التردد أي الفاصل الزمني الذي يجب أن تأخذ فيه هذه العينات حتى يتسنى لنا عن طريق معالجة العينات أن نعرف الإشارة الأصلية أي المتواترة.

تعطي المبرهنة إجابة على هذا السؤال حيث تقول أنه إذا كان لدينا إشارة متواترة يكون أكبر تردد فيها يساوي $f_{max}$ وأصغر تردد هو صفر فإن أخذ العينات يجب أن يتم بتردد أكبر من ضعف $f_{max}$ أي بتررد $f_a=2f_{max}$.

أمثلة

• 

  صورة تراعي مبرهنة الاستعيان

• 

  صورة لا تراعي مبرهنة الاستعيان. لاحظ التقوسات التي تبدو وكأنها موجودة على سقف المنزل