مفاعلة كهربائية
المفاعلة في المكثفات والملفات وحدتها الأوم لكنها تختلف عن المقاومة فالمقاومة تخضع لقانون أوم بغض النظر عن قيمة تردد تيار الدائرة الكهربية بينما المفاعلة فهي قيمة تخيلية تمثل معاكسة الملف والمكثف للتيار الذي يمر بهما، علما بأن قيمتهما تتغيران بتغير تردد التيار.[1]
رياضيا
في حالة التيار المستمر
ولذلك في حالة التيار المستمر فإن مفاعلة الملف تكون صفرا وبذلك يعتبر في الدائرة كما لو كان دارة قصر، أي لايحدث أي فقد للطاقة الكهربائية أو انبعاث حرارة وذلك لإن:
حيث هي مفاعلة الملف بال أوم وهي دائما قيمة موجبة تمثل تأخر التيار عن الجهد.
f هي تردد بالهيرتز
L هي تحريض الملف بال هنري (وحدة قياس)
بينما يتصرف المكثف في حالة التيار المستمر كما لو كان دائرة مفتوحة أي لا يمر في التيار بسبب أن:
حيث Xc هي مفاعلة المكثف بالأوم وهي دائما قيمة سالبة تعبر عن أسبقية التيار على الجهد.
F هي سعة المكثف بالفاراد
أما المفاعلة الكلية في أي دائرة فتكون:
وبما أن المفاعلة الكلية للمكثف دائما سالبة اصطلح على وضع الإشارة مسبقا فتصبح هكذا
ويمكن الاستدلال بقيمة المفاعلة على نوع المكون الإلكتروني فهو ملف إذا كانت قيمة المفاعلة موجبة ومكثف حينما تكون سالبة ومقاوم إذا ما ساوت الصفر.
وبذلك تكون المعاوقة الكلية للدائرة هي حصيلة جمع متجهات بين جملة المقاومات وجملة المفاعلات في الدائرة:
مقدار تساوي:
| وحدات الكهرومغناطيسية القياسية
| ||||
|---|---|---|---|---|
| رمز الكمية | الكمية | الواحدة | رمز الواحدة | الأبعاد |
| I | التيار | أمبير (وحدات قياسية) | A | A |
| Q | شحنة كهربائية | كولوم | C | A·s |
| V | فرق الجهد | فولت | V | J/C = kg·m2·s−3·A−1 |
| R، Z، X | مقاومة، معاوقة، مفاعلة بالترتيب | أوم | Ω | V/A = kg·m2·s−3·A−2 |
| ρ | مقاومية | أوم متر | Ω·m | kg·m3·s−3·A−2 |
| P | القدرة الكهربائية | واط | W | V·A = kg·m2·s−3 |
| C | سعة كهربائية | فاراد | F | C/V = kg−1·m−2·A2·s4 |
| مرانة | مقلوب الفاراد | F−1 | kg·m2·A−2·s−4 | |
| سماحية | فاراد لكل متر | F/m | kg−1·m−3·A2·s4 | |
| Y ، G ، B | مسامحة، مواصلة، مطاوعة | سيمنز | S | Ω−1 = kg−1·m−2·s3·A2 |
| موصلية | سيمنز في متر | S/m | kg−1·m−3·s3·A2 | |
| تدفق مغناطيسي | فيبر | Wb | V·s = kg·m2·s−2·A−1 | |
| B | كثافة التدفق المغناطيسي أو المجال المغناطيسي | تيسلا | T | Wb/m2 = kg·s−2·A−1 |
| H | شدة المجال المغناطيسي | أمبير لكل متر | A/m | A·m−1 |
| ممانعة | أمبير لكل فيبر | A/Wb | kg−1·m−2·s2·A2 | |
| L | محاثة مغناطيسية | هنري | H | Wb/A = V·s/A = kg·m2·s−2·A−2 |
| نفاذية | هنري على متر | H/m | kg·m·s−2·A−2 | |
| قابلية مغناطيسية | (بلا أبعاد) | χ | - | |
المفاعلة في وجود تيار متردد
(يتطلب فهم المفاعلة لمكثف أو لملف كهربائي معرفة بالأعداد المركبة وحساباتها)
المفاعلة هي الجزء التخيلي للمقاومة الكهربائية. وستنباط المعادلات الخاصة بها نجده في موضوعي مقاومة كهربائية وتيار متردد. ونتعامل مع تلك المسألة عادة بافتراض أن تردد التيار يكون في هيئة موجة جيبية.
في تلك الحسابات تستخدم المفاعلة لحساب مطال التيار المتردد وكذلك لحساب تغير طوره الموجي في دائرة كهربائية باعتبار التيار المتردد في شكل موجة جيبية. ويرمز للمعاوقة بالرمز .
ونحتاج إلى كلا الإثنين: للمفاعلة والمقاومة لحساب المعاوقة الكهربائية .
وقد تغلب قيمة أو مفعول أحداهما في دائرة كهربائية ولكن معرفة قيمة كل منهما تعرفنا عما إذا كان في الإمكان أهمالها أم لا.
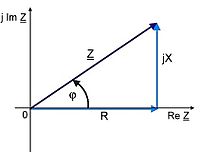
والمعاوقة هي:
- حيث
- المعاوقة الكهربائية، ونقيسها بالأوم.
- المقاومة الكهربائية، وتقاس بالأوم.
- المفاعلة الكهربائية، وتقاس بالأوم.
وكل من القيمة المطلقة والطور يعتمد على المقاومة و المفاعلة (الجزء التخيلي للمعاوقة).
- حيث
وقيمتها هي حاصل قسمة مطال الجهد الكهربائي على مطال التيار الكهربائي، بينما الفرق بين طور الجهد وطور التيار يعطي الطور.
- إذا كانت , فتسمى المفاعلة «مفاعلة محاثية»
- وإذا كانت , فتسمى المفاعلة «مفاعلة مقاومية»
- وإذا كانت , فتسمى المفاعلة «مفاعلة مكثفية».
الملف
بالنسبة إلى «ملف» ذو محاثة L، تبلغ المعاوقة:
حيث j الوحدة التخيلية.
ومفاعلتها، وتسمى أيضا الجزء التخيلي للمعاوقة (للمقاومة، واسمها بالألمانية «مقاومة عمياء» أو «مقاومة خفية»)، تعطى بالمعادلة:
ومقاومتها التخيلية تكون مقاومة خطية للتيار المتردد (ولا تعتمد على الجهد ولا على شدة التيار)، ولكنها تزداد بزيادة التردد f (وبالتالي بزيادة التردد الزاوي ).
المكثف
بالنسبة إلى مكثف ذو سعة كهربائية C:
المقاومة التخيلية للمكثف تساوي:
وهي تمثل الجزء التخيلي من المعاوقة الكهربائية
وكما نرى تكون المقاومة التخيلية لمكثف مثالي ذو سعة C مقاومة خطية للتيار المتردد، ولكنها تقل بزيادة التردد.
يلاحظ أن المقاومة التخليلية للمكثف ذات إشارة سالبة. والمعنى الفيزيائي لهذا هو أنه بين الجهد والتيار يوجد انزياح طور معاكس بينهما.
انظر أيضا
المراجع
- ^ Les circuits à courant alternatif sur le site de l'IIHE. نسخة محفوظة 18 نوفمبر 2017 على موقع واي باك مشين.