نقاط مشتركة بدائرة

في الهندسة الرياضية، تتصف مجموعةٌ من النقاط بـ«الدائرية» إذا كانت نقاطاً مشتركة بدائرة. أي أنها تقع على محيط دائرة مشتركة. بنحوٍ مكافئ، هناك نقطةً بُعْدُها بين كل نقطة أخرى من مجموعة النقاط متساوٍ. تُسمّى هذه النقطة مركز الدائرة. حتى تشتركَ نقاطٌ بدائرةٍ، على المنصفات العمودية لكل نقطتين أن تلتقي في نقطة واحدة هي مركز الدائرة المحيطة بالنقاط، والعكس صحيح.

حالات وعلاقات الكائنات الهندسية فيما بينها
تسامُتٌ	تلاقٍ
توازٍ	تعامد
تنصيف	انطباقٌ
دَائريَّةٌ	تماس
السعي نحو اللانهاية	انعدامٌ
مُخالَفَةٌ	اشتراك في مستوى

نقاط مشتركة بدائرة، محاور القطع المستقيمة المشكلة بالنقط تتقاطع في مركز الدائرة

للنقاط المشتركة بدائرة تكون الزاوية $\alpha$ متماثلة.

مبرهنات

كل نقطة متساوية البعد عن طرفي قطعة مستقيمة تكون واقعة على منصفها العمودي.

البرهان: إذا كانت النقطة O متساوية البعد عن طرفي PQ أي OP = OQ، نرسم OM حيث M منتصف PQ، عندئذٍ:

MP = MQ
OP = OQ
OM ضلع مشتركة

وبالتالي المثلثان OMP وOMQ متطابقان بحسب حالة (ضلع.ضلع.ضلع)، ومنه

$\widehat{OMP}=\widehat{OMQ}$

، لكن

$\widehat{OMP}$

تشكل مع

$\widehat{OMQ}$

زاوية مستقيمة، وبالتالي

$\widehat{OMP}=180/2=90$

، ومنه OM منصف عمودي لـ PQ، وO واقعة عليه.

كل نقطة من منصف عمودي لقطعة مستقيمة متساوية البعد عن طرفيها.

البرهان: بفرض PQ قطعة مستقيمة محورها OM، فإن :

MP=MQ
OM ضلع مشتركة
$\widehat{OMP}=\widehat{OMQ}=90$ ومنه المثلثان OMP وOMQ مثلثان متطابقان بحسب حالة (ضلع.زاوية.ضلع)، ومن التطابق ينتج أن OP = OQ.

المضلعات الدائرية

المثلثات

رؤوس أي مثلث تشترك بدائرة، الدائرة المشتركة تسمى الدائرة المحيطة بالمثلث، ويحسب نصف قطرها، بأطوال أضلاع المثلث a، b، c: $R=\sqrt{\frac{a^2{b}^2{c}^2}{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}}.$

الرباعيات الدائريات

المقالة الرئيسية: رباعي دائري

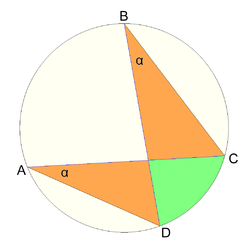
يحاط المضلع ABCD بدائرة إذا وفقط إذا كانت $\mathrm{\angle }CAD=\mathrm{\angle }CBD$ ويحسب نصف قطر الدائرة المحيطة بدلالة أطوال الأضلاع a، b، c، d، ونصف المحيط S حيث $S=\frac{a+b+c+d}{2}$ ، بالقانون: $R=\frac{1}{4}\sqrt{\frac{(a.b+c.d)(a.c+b.d)(a.d+b.c)}{(s-a)(s-b)(s-c)(s-d)}}$ وقد استنتج هذا القانون لأول مرة من قبل العالم الهندي ڤاتاسِّيري پاراميشڤارا في القرن الخامس عشر. وبفرض ABCD شكل رباعي، وبحسب مبرهنة بطليموس فإنه دائري إذا وفقط إذا كان جداء القطرين يساوي مجموع جداءي كل ضلعين متقابلين أي أن: $AC.BD=AB.CD+AD.BC$. وإذا كانت النقطة X هي نقطة تلاقي القطرين ACو BD فإن ABCD شكل دائري إذا وفقط إذا كان: $AX.XC=BX.XD$. تعرف هذه النظرية باسم قوة نقطة.

مضلعات ذوات n ضلعاً

بشكل عام، تكون المضلعات دائرية إذا كانت منصفاتها العمودية تلتقي في نقطة واحدة، وتلك النقطة هي مركز الدائرة.