|
تضامنًا مع حق الشعب الفلسطيني |
حسابات الطاقة الكهربائية للتيار ثلاثي الطور

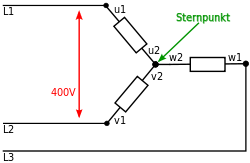

في الهندسة الكهربائية، تمتلك أنظمة الطاقة الكهربائية ثلاثية الأطوار ثلاثة موصلات على الأقل تحمل الجهد المتردد يكون جهد كل طرف متأخر عن جهد الطرف الأخر بمقدار ثلث الزمن الكامل. يمكن توصيل النظام الثلاثي إما ستار أو دلتا.
تسمح توصلية ستار باستخدام جهدين مختلفين بين الثلاث موصلات، فعلى سبيل المثال:
- في الأنظمة التي تعمل (220/380) فولت يكون فيها الجهد بين كل فازه (طور) والنيوترال 220 بينما 380 بين أي فيزتين (طورين).
- في الأنظمة التي تعمل (230/400) فولت يكون فيها الجهد بين كل فازه (طور) والنيوترال 230 بينما 400 بين أي فيزتين (طورين).
في حين لا توفر توصيله الدلتا غير جهد واحد لكنه يوفر تكرارية تصل إلى 57.7% تجعل العزم أفضل.[1] قد يصبح التيار التوافقي في الخط المحايد كبير جدا في حالة توصيل الأحمال غير الخطية.
تعريفات
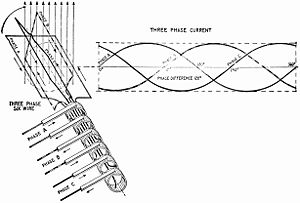


في طوبولوجيا توصيلة ستار، مع تسلسل الدوران L1 - L2 - L3، يمكن حساب الفولتية اللحظية المتغيرة مع الوقت لكل مرحلة A,C,B على التوالي من خلال المعادلة التالية:
حيث
- : هو الجهد الأقصى.
- : هي الزاوية بالدرجات.
- : الزمن بالثواني
- : التردد ويساوي ععدد الدورات في الثانية الواحدة
الأحمال المتوازنة
بشكل عام، في أنظمة الطاقة الكهربائية يتم توزيع الأحمال بالتساوي على الأطوار. من المعتاد مناقشة نظام متوازن أولاً ثم وصف آثار الأنظمة غير المتوازنة باعتبارها انحرافات عن الحالة الأولية.
نقل الطاقة
توفر الطاقة ثلاثية الطور ميزة أن الحمل المكون من مقاومات فقط يكون ثابت من المعادلة:
بما أن
للتبسيط يمكن القول أن
ومن هنا نجد أن الطاقة الكلية تساوي:
لا تختلف الطاقة بمرور الوقت. ومع الأخذ في الاعتبار أن تكون الطاقة الكلية تساوي:
- .
لا يجب أن يكون الحمل مكون من مقاومات فقط لذلك:
لذلك يكون أقصى تيار:
عند تطبيق ما سلف على الثلاث أطوار نجد أن:
لذلك تكون الطاقة تساوي:
يمكن كتابتها بالشكل التالي:
بذلك تكون الطاقة الكلية:
بعد اختصار المعادلة السابقة يكون الناتج هي المعادلة التالية
أو يمكن كتابتها بالشكل التالي
أو الشكل التالي
- .
تيار المحايد
لا يسير تيار في النيوترال (المحايد) في حالة كون الأحمال متساوية في كل الأطوار. فمع تطبيق قوانيون كيرشوف، يظهر أن تيار النيوترال هو مجموع المتجه المقلوب لتيارات الخط.
وبما أن إذا:
الأنظمة غير المتزنة

من الناحية العملية، نادراً ما تكون للأنظمة أحمال متزنة تمامًا في التيارات، الجهد والممانعات في جميع المراحل الثلاث. يتم تبسيط تحليل الحالات غير المتوازنة بشكل كبير من خلال استخدام تقنيات المكونات المتماثلة حيث يتم تحليل النظام غير المتوازن باعتباره تراكب ثلاثة أنظمة متوازنة، لكل منها التسلسل الإيجابي أو السلبي أو صفر للجهود المتوازنة. عند تحديد أحجام الأسلاك في نظام ثلاثي الأطوار لا نحتاج سوى معرفة حجم الطور وتيار النيوترال. يمكن تحديد التيار المحايد عن طريق إضافة التيارات ثلاثية الطور معًا كأعداد معقدة ومن ثم تحويلها من مستحاثات. إذا كانت تيارات جذر متوسط التربيع (RMS) ثلاثية المراحل هي: يتم اختصارها إلى ، و . لتكون بذلك قيمة تيار النيوترال المتوسط يساوي:
يمكن اختصارها إلى الشكل التالي:[2]
لتكون بذلك القيمة المطلقة له تساوي:
الأحمال غير الخطية
في حالة الأحمال الخطية، يحمل النيوترال التيار نتيجة اختلاف التوازن بين الأطوار. تولد الأجهزة التي تستخدم مقوم- مكثف (مثل مزود الطاقة لأجهزة الكمبيوتر، الأجهزة مكتبية وما شابه) توافقيات من الدرجة الثالثة.[3][4]
قياسات النظام
من الممكن قياس القدرة في نظام ثلاثي الطور باستخدام محولين في حالة عدم وجود نيوترال أو ثلاثة محولات في حالة وجود نيوترال.[5] تنص مبرهنة بلونديل على أن عدد عناصر القياس المطلوبة أقل من عدد الموصلات الحاملة للتيار.[6]
انظر أيضًا
المصادر
- ^ "Archived copy" (PDF). مؤرشف (PDF) من الأصل في 2013-05-13. اطلع عليه بتاريخ 2012-11-21.
{{استشهاد ويب}}: صيانة الاستشهاد: الأرشيف كعنوان (link) public domain - ^ Keljik، Jeffrey (2008). Electricity 3: Power Generation and Delivery. Clifton Park, NY: Cengage Learning/Delmar. ص. 49. ISBN:1435400291.
- ^ Lowenstein، Michael. "The 3rd Harmonic Blocking Filter: A Well Established Approach to Harmonic Current Mitigation". IAEI Magazine. مؤرشف من الأصل في 2011-03-27. اطلع عليه بتاريخ 2012-11-24.
- ^ Enjeti، Prasad. "Harmonics in Low Voltage Three-Phase Four-Wire Electric Distribution Systems and Filtering Solutions" (PDF). Texas A&M University Power Electronics and Power Quality Laboratory. مؤرشف (PDF) من الأصل في 2010-06-13. اطلع عليه بتاريخ 2012-11-24.
- ^ "Measurement of three-phase power with the 2-wattmeter method". مؤرشف من الأصل (PDF) في 2020-07-03.[وصلة مكسورة]
- ^ "THE TWO-METER WATTMETER METHOD" (PDF). مؤرشف من الأصل (PDF) في 19 مارس 2013. اطلع عليه بتاريخ أكتوبر 2020.
{{استشهاد ويب}}: تحقق من التاريخ في:|تاريخ الوصول=(مساعدة)