|
تضامنًا مع حق الشعب الفلسطيني |
تحويلة ستار دلتا
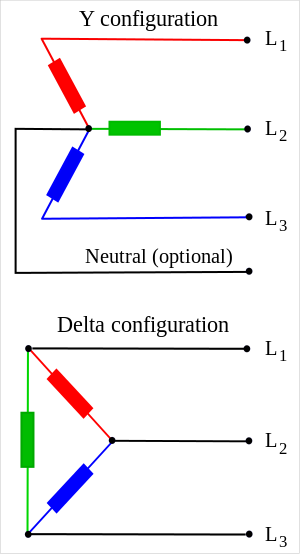
تحويلة ستار دلتا (تحويلة Y-Δ)، يمكن تسميتها أيضا بتحويلة وي دلتا، هي طريقة رياضية لتبسيط تحليل الدوائر الكهربائية. تم اشتقاق الاسم من أشكال مخططات الرسم البياني فستار تشبة الحرف Y ودلتا هو حرف يوناني قديم Δ. يرجع الفضل في اكتشاف تلك الطريقة إلى عالم الرياضيات إيرلندي المولد أمريكي الجنسية آرثر إدوين كينلي الذي اكتشفها في عام 1899.[1] تستخدم الطريقة على نطاق واسع في تحليل الدوائر الكهربائية ثلاثية الطور.
يمكن اعتبار تحويلة ستار دلتا كحالة خاصة من تحويلة الشبكة النجمية لثلاثة مقاومات. في الرياضيات، تلعب التحويلة دوراً هامّاً في نظرية الرسوم البيانية المستوية الدائرية.[2]
التسمية

للتحويلة مجموعة كبيرة من الأسماء المشهورة بها، يستند معظمها إلى الأشكال. فعلى سبيل المثال، يمكن أن يطلق على الشكل Y ستار، وي أو تي، بينما يمكن تسمية رمز Δ دلتا، المثلث، باي Π أو ميش. لذلك تحويلة ستار دلتا هي نفسها وي دلتا، ستار ميش أو T-Π.
التحويلات

تستخدم الطريقة لإيجاد دائرة مكافئة بسيطة بثلاثة أطراف للدوائر المعقدة. في دوائر الدلتا يشترك كل عنصرين في عقدة بينما في حالة الستار يشترك الثلاث عناصر في عقدة واحدة.
تحويل من دلتا إلى ستار
الفكرة العامة هي إيجاد المقاومة لأي عنصرين , بشرط أن يكونوا متجاورين من المعادلة التالية:
حيث هي المقاومة الكلية لدائرة دلتا Δ.
لتحويل كل عنصر من دلتا إلى ستار من المعادلة التالية:
تحويل من ستار إلى دلتا
الفكرة العامة هي الحصول على للدائرة Δ من المعادلة التالية:
حيث:
هي مجموع كل عنصرين في الدائرة ستار، بينما هي العنصر المراد تحويلة إلى دلتا. بذلك تصبح المعادلات كالتالي:
أو بالشكل التالي:
تبسيط الدوائر
يمكن أن تستخدم التحويلة أكثر من مرة في نفس الدائرة المعقدة لتبسيطها، فعلى سبيل المثال يمكن استخدام تحويلة دلتا ستار لحل عقدة ثم تحويلة ستار دلتا لتبسيط عقدة أخرى، كما هو موضح في الأشكال التالية:


نظرية المخططات
في نظرية المخططات، تعني تحويلة ستار دلتا استبدال مخطط Y إلى مخطط Δ مع الاحتفاظ بقيمة المقاومات المكافئة، لكن ليس عدد العناصر. فعلى سبيل المثال، يمكن تحويل 3 أشكال دلتا إلى شكل Y وحيد في ثلاث خطوات.
البرهنة
معادلات تحويل دلتا إلى ستار

لتحويل العناصر من الدائرة دلتا Δ إلى في الدائرة ستار Y. يتم ربط بداية كل عنصر ونهايته بالعقد. يمكن ملاحظة أن العقد N1 و N2 و N3 يكونوا مثلث Δ:
للتبسيط، نجعل هي حاصل جمع العناصر التالية .
المقاومة بين العقدة N1 والعقدة N2 في الدائرة Δ:
تكون المقاومة المكافئة في الدائرة Y:
بالتالي:
- (1)
وبالمثل في حالة :
- (2)
وبالمثل أيضا في حالة :
- (3)
وبالتالي يمكن استنتاج قيم عن طريق عمليات الجمع والطرح.
على سبيل المثال يمكن جمع كل من معادلة (1) و (3) ثم طرح الناتج من معادلة (2)، كالتالي:
لتكون المعادلة النهائية بالشكل التالي:
- (4)
- (5)
- (6)
معادلات تحويل ستار إلى دلتا
نجعل
- .
يمكن استخلاص معادلات Δ من Y:
- (1)
- (2)
- (3)
بضرب كل معادلتين، يكون شكل المعادلات كالتالي:
- (4)
- (5)
- (6)
ثم جمع المعادلات، لتكون المعادلة كالتالي:
- (7)
بأخذ عامل مشترك في الطرف الأيمن، فتظهر ثم اختصارها مع الموجودة في المقام.
- (8)
بعد قسمة (8) على (1):
وبالتالي نحصل على في دائرة دلتا. وبالمثل قسمة (8) على (2) مرة وعلى (3) مرة أخرى لنحصل على ,
انظر أيضا
المصادر
- ^ A.E. Kennelly, "Equivalence of triangles and three-pointed stars in conducting networks", Electrical World and Engineer, vol. 34, pp. 413–414, 1899.
- ^ E.B. Curtis, D. Ingerman, J.A. Morrow, Circular planar graphs and resistor networks, Linear Algebra and its Applications, vol. 238, pp. 115–150, 1998. نسخة محفوظة 24 سبتمبر 2015 على موقع واي باك مشين.