|
تضامنًا مع حق الشعب الفلسطيني |
ميكانيكا الكم
| جزء من سلسلة مقالات حول |
| ميكانيكا الكم |
|---|
| بوابة ميكانيكا الكم |
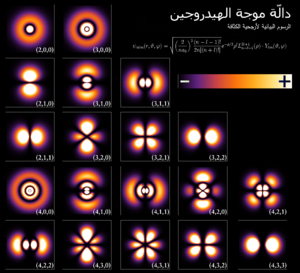
لا يمكن لميكانيكا الكم أن تتنبأ بالموقع الدقيق للجسيم في الفضاء، وإنما فقط احتمال العثور عليه في مواقعَ مختلفةٍ.[1] تمثل المناطق الأكثر سطوعًا احتمالًا أعلى لإيجاد الإلكترون.
ميكانيكا الكم[ar 1] أو ميكانيك الكم[ar 2] أو الميكانيك الكمومي[ar 3] أو الفِيقِيَاءُ (أصلها من فاق يفوق، لأنّها تبحث في عالم الظواهر فائقة الصغر وفائقة السرعة)[ar 4] هي نظرية رئيسة في الفيزياء توفر وصفًا للخصائص الفيزيائية للطبيعة على مقياس الذرات والجسيمات دون الذرية.[2] وميكانيكا الكم (أو الحركة الكمومية) هي الأساس الذي تقوم عليه فيزياء الكم وكيمياء الكم ونظرية الحقل الكمومي وتقانة الكم وعلوم المعلومات الكمومية.
تُسمَّى مجموعة النظريات التي كانت موجودةً قبل ظهور ميكانيكا الكم الفيزياء الكلاسيكية، وهي تصف جوانبَ عديدةً من الطبيعة باعتماد مقياس عياني، ولكنها لا تصلح لوصف الظواهر الحاصلة في المقاييس الذرية ودون الذرية. يمكن اشتقاق معظم النظريات في الفيزياء الكلاسيكية من ميكانيكا الكم مثل تقريب صالح على نطاق واسع (عياني).[3]
تختلف ميكانيكا الكم (أو الحركة الكمومية) عن الفيزياء الكلاسيكية في اقتصار الطاقة والزخم والزخم الزاوي (عزم الدوران) والكميات الأخرى من نظام مقيد على القيم المنفصلة (التكميم)، وللأجسام فيها خصائص الجسيمات والموجات معًا (ازدواجية موجة جسيم)؛ وهناك حدود لمدى دقة التنبؤ بقيمة الكمية المادية قبل قياسها، بالنظر إلى مجموعةٍ كاملةٍ من الشروط الأولية (مبدأ اللايقين).
طُوِّرت ميكانيكا الكم تدريجيًا انطلاقًا من نظرياتٍ تشرح الملاحظات التي لا يمكن التوفيق بينها وبين الفيزياء الكلاسيكية، مثل حل ماكس بلانك لمشكلة إشعاع الجسم الأسود في عام 1900، والمطابقة بين الطاقة والتردد في ورقة ألبرت أينشتاين عام 1905 والتي فسرت التأثير الكهروضوئي.[4] أدت هذه المحاولات المبكرة لفهم الظواهر العيانية -والمعروفة الآن باسم «نظرية الكم القديمة»- إلى التطور الكامل لميكانيكا الكم في منتصف عشرينيات القرن الماضي بواسطة نيلز بور وإرفين شرودنغر وفيرنر هايزنبيرغ وماكس بورن وبول ديراك وآخرين. صيغت النظرية الحديثة في أشكال رياضية مختلفة طورت خصيصًا لذلك. يوفر كيان رياضي -هو أحد هذه الأشكال الرياضية، ويسمى دالة الموجة- معلوماتٍ -على شكل سعاتٍ احتماليةٍ- حول قياسات طاقة الجسيم، وزخمه، والخصائص الفيزيائية الأخرى التي قد يتسم بها.
نظرة عامة ومفاهيم رئيسة
تسمح ميكانيكا الكم بحساب خصائص الأنظمة الفيزيائية وسلوكها. وهي تطبق عادةً على الأنظمة المجهرية: كالجزيئات والذرات والجسيمات دون الذرية. وقد أُثبتت قدرتها على الاحتفاظ بالجزيئات المعقدة التي تحتوي على آلاف الذرات،[5] ولكن تطبيقها على البشر يثير مشكلاتٍ فلسفيةٍ، مثل صديق ويغنر، ويظل تطبيقها على الكون كله تخمينيًا.[6] تحقق العلماء من تنبؤات ميكانيكا الكم من خلال التجربة بدرجةٍ عاليةٍ من الدقة.[note 1]
تكمن السمة الرئيسة لميكانيكا الكم في عدم قدرتها على التنبؤ على وجه اليقين بما سيحدث، وتقديمها احتمالاتٍ عوضًا عن ذلك. يُحسَب الاحتمال رياضيًا بأخذ مربع القيمة المطلقة لعدد مركب، والمعروف باسم "سعة الاحتمال". يُعرف هذا باسم قاعدة بورن، والتي سميت على اسم الفيزيائي ماكس بورن. فمثلًا يمكن وصف جسيمٍ كميٍّ مثل الإلكترون بواسطة دالة موجية تربط كل نقطةٍ في الفضاء بسعةٍ احتمالية. إن تطبيق قاعدة بورن على هذه السعات يعطي دالة الكثافة الاحتمالية للموقع الذي سيوجد فيه الإلكترون عند إجراء تجربةٍ لتعيين مكانه، وهذا أفضل ما يمكن للنظرية أن تقدمه؛ فهي لا يمكنها تحديد موقع الإلكترون على وجه اليقين. وتقوم معادلة شرودنغر بربط مجموعة السعات الاحتمالية لموقع لإلكترون المتعلقة بلحظةٍ زمنيةٍ معينةٍ يمجموعة السعات الاحتمالية المتعلقة بلحظةٍ زمنيةٍ أخرى.
إحدى نتائج القواعد الرياضية لميكانيكا الكم هي المقايضة حول إمكانية التنبؤ بين الكمومات المختلفة القابلة للقياس. تشير الصيغة الأكثر شهرةَ لمبدأ اللايقين هذا إلى أنه -وبغض النظر عن كيفية تحضير الجسيم الكمي أو مدى دقة ترتيب التجارب عليه- فإن من المستحيل وجود تنبؤٍ دقيقٍ لقياس كلا موقعه وزخمه في الوقت نفسه.
تعد ظاهرة التداخل الكمي إحدى النتائج الأخرى للقواعد الرياضية لميكانيكا الكم، وهي غالبًا ما تتضَّح من خلال تجربة الشق المزدوج. في النسخة الأصلية من هذه التجربة يُضيء مصدر ضوءٍ متسقٍ -كشعاع ليزر مثلًا- صفيحةً مثقوبةً بشقين متوازيين، ويلاحظ الضوء الذي يمر عبر الشقين على شاشةٍ تقع خلف الصفيحة المثقوبة.[2]:1.1–1.8[7]:102–111 تتسبب الطبيعة الموجية للضوء في تداخل موجات الضوء التي تعبر الشقين، مما ينتج عنه نطاقات ساطعة ومظلمة على الشاشة؛ وهي نتيجة لا يمكن توقعها إذا كان الضوء يتكون من جسيماتٍ كلاسيكية.[7] ومع ذلك دائمًا ما يُمتص الضوء على الشاشة عند نقاطٍ منفصلةٍ كجسيماتٍ فرديةٍ بدلًا من موجاتٍ؛ ويَظهر نمط التداخل من خلال الكثافة المتغيرة لاصطدامات هذه الجسيمات على الشاشة. علاوةً على ذلك وَجدت نسخٌ لاحقة للتجربة تتضمن وضع كاشفاتٍ عند الشقوق أن كل فوتون مكتشَفٍ يمر من خلال شقٍّ واحدٍ (كما هو الحال مع الجسيم الكلاسيكي)، وليس عبر كلا الشقين (كما الحال بالنسبة للموجة).[7]:109[8][9] ومع ذلك فإن مثل هذه التجارب تظهر أن الجسيمات لا تشكل نمط التداخل إذا اكتشف المرء الشق الذي تمر من خلاله. عُثر على جسيماتٍ أخرى ذات مقاسٍ ذريٍّ -مثل الإلكترونات- تُظهر السلوك نفسه عند إطلاقها نحو شقٍّ مزدوج.[2] وهو السلوك الذي يُعرف بازدواجية موجة-جسيم.
تنبأت ميكانيكا الكم بظاهرةٍ أخرى غير بدهيّةٍ هي ظاهرة النفق الكمومي، وفيها يمكن للجسيم الذي يتقدم باتجاه حاجز جهدي أن يتخطاه ولو كانت طاقته الحركية أصغر من الحد الأقصى المحتمل.[10] بينما في الميكانيكا الكلاسيكية سيجري احتجاز هذا الجسيم. ثمة نتائج عديدة مهمة للنفق الكمي مرتبطة بالاضمحلال الإشعاعي، وبالاندماج النووي في النجوم، وتطبيقات مثل مجهر المسح النفقي وثنائي المساري النفقي.[11]
عندما تتفاعل الأنظمة الكمومية يمكن أن تكون النتيجة إنشاء تشابك كمي: فتصبح خصائصها متشابكةً لدرجة أن وصف الكل بالاعتماد على الأجزاء الفردية فقط لا يعود ممكنًا. دعا إرفين شرودنغر التشابكَ «... السمةَ المميزةَ لميكانيكا الكم التي تفرض خروجها بالكامل عن خطوط الفكر الكلاسيكية».[12] يتيح التشابك الكمي الخصائص غير البدهيّةِ للتخاطر الزائف الكمي، ويمكن أن يكون موردًا قيّمًا في بروتوكولات الاتصال، مثل توزيع المفاتيح الكمومية والترميز فائق الكثافة.[13] وعلى عكس الاعتقاد الخاطئ الشائع لا يسمح التشابك بإرسال إشاراتِ أسرع من الضوء، كما يتضح من نظرية عدم الاتصال.[13]
ثمة احتمال آخر ممكن ينتج عن التشابك الكمي هو اختبار «المتغيرات الخفية»، وهي خصائص افتراضية أكثر جوهريةً من الكمومات التي تتناولها نظرية الكم نفسها، ومن شأنها أن تسمح بتنبؤاتٍ أكثر دقةً مما توفره نظرية الكم. أظهرت مجموعة من النتائج -وأهمها مبرهنة بل- أن الفئات العريضة من نظريات المتغيرات الخفية هي في الواقع غير متوافقةٍ مع فيزياء الكم. وفقًا لمبرهنة بل إذا كانت الطبيعة تعمل بالفعل طبقًا لأي نظريةٍ لمتغيراتٍ محليةٍ خفيةٍ، فإن نتائج "اختبار بل" ستكون مقيَّدةً بطريقةٍ معينةٍ قابلةٍ للقياس الكمي. أجري العديد من اختبارات بل باستخدام جسيماتٍ متشابكةٍ، وقد أظهرت نتائجَ غير متوافقةٍ مع القيود التي تفرضها المتغيرات الخفية المحلية.[14][15]
من غير الممكن تقديم هذه المفاهيم بأكثرَ من طريقةٍ سطحيةٍ دون تقديم الرياضيات الفعلية المعنية؛ لا يتطلب فهم ميكانيكا الكم معالجة الأعداد المركبة فحسب، بل أيضًا الجبر الخطي والمعادلات التفاضلية ونظرية الزمر وموضوعاتٍ أخرى أكثر تقدمًا.[note 2] وفقًا لذلك ستقدم هذه المقالة صياغةً رياضيةً لميكانيكا الكم ومسحًا لتطبيقاتها على بعض الأمثلة المفيدة التي جرت دراستها كثيرًا.
صياغة رياضية
تكون حالة النظام الميكانيكي الكمومي في الصيغة الرياضية الدقيقة لميكانيكا الكم عبارةً عن متجه ينتمي إلى فضاء هيلبرت العقدي (القابل للفصل) . يُفترض أن هذا المتجه يجري تطبيعه ضمن الجداء الداخلي لفضاء هيلبرت، أي إنه يخضع لـ، وهو محدد جيد حتى عدد معقد من المعامل 1 (المرحلة العامة)، أي و تمثل النظام الفعلي نفسه. بعبارةٍ أخرى الحالات المحتملة هي نقاط في الفضاء الإسقاطي لفضاء هيلبرت، والتي تسمى عادةً فضاء الإسقاط العقدي. تعتمد الطبيعة الدقيقة لفضاء هيلبرت على النظام؛ فعلى سبيل المثال لوصف الموقع والزخم، فإن فضاء هيلبرت هو فضاء الدوال العقدية القابلة للتكامل المربع ، بينما فضاء هلبرت لمغزل بروتون واحد هو ببساطة فضاء المتجهات العقدية ثنائية الأبعاد مع الجداء الداخلي المعتاد.
يجري تمثيل الكمومات المادية ذات الأهمية -الموقع، والزخم، والطاقة، والمغزلية- بواسطة المراقبات، وهي مؤثرات خطية هيرميتية (بتعبيرٍ أدق مساعد ذاتي) تعمل في فضاء هيلبرت. يمكن أن تكون الحالة الكمومية متجهًا ذاتيًا يمكن ملاحظته، وفي هذه الحالة يطلق عليها اسم حالة ذاتية، وتتوافق القيمة الذاتية المرتبطة مع قيمة ما يمكن ملاحظته في تلك الحالة الذاتية. ستكون الحالة الكمومية مزيجًا خطيًا من حالاتٍ ذاتيةٍ عموماً، والمعروف باسم التراكب الكمومي. عندما يجري قياس ما يمكن ملاحظته، ستكون النتيجة واحدة من قيمها الذاتية مع الاحتمال الذي قدمته قاعدة بورن: في أبسط الحالات، تكون القيمة الذاتية غير منهارةٍ ويجري إعطاء الاحتمال بواسطة ، وفيه هو المتجه الذاتي المرتبط به. تنهار القيمة الذاتية عادةً ويُعطى الاحتمال باستعمال ، وفيه هو الإسقاط على الفضاء الذاتي المرتبطة به. في الحالة المستمرة تعطي هذه الصيغ بدلاً من ذلك كثافة الاحتمال.
إذا تُوُصِّلَ -بعد القياس- إلى النتيجة فيُفترض أن الحالة الكمومية تنهار إلى ، في الحالة غير المنهارة أو في الحالة العامة. وعليه فإن الطبيعة الاحتمالية لميكانيكا الكم تنبع من فعل القياس، وهو أحد أصعب جوانب الأنظمة الكمومية قابليةً للفهم، وقد كان الموضوع الرئيسي في مناظرات بور-أينيشتاين الشهيرة، حيث حاول فيها العالمان توضيح هذه المبادئ الرئيسة عن طريق التجارب الفكرية. وفي العقود التي تلت صياغة ميكانيكا الكم جرت دراسة مسألة ماهية «القياس» على نطاقٍ واسع، وصيغت تفسيرات جديدة لميكانيكا الكم تتخلص من مفهوم «انهيار الدالة الموجية» (انظر على سبيل المثال تفسير العوالم المتعددة). الفكرة الأساس هي أن دوال الموجة الخاصة بنظامٍ كميٍّ وجهاز قياسٍ تتشابك عندما يتفاعلان، وحينها يتوقف النظام الكمي الأصيل عن الوجود بصفته كيانًا مستقلًا. لمزيدٍ من التفاصيل راجع مقال القياس في ميكانيكا الكم.[18]
جرى وصف النمو الزمني للحالة الكمومية بواسطة معادلة شرودنغر:
وتشير فيها إلى هاملتوني يمكن ملاحظته المقابلة للطاقة الكلية للنظام، و هو ثابت بلانك المختزَل. يُدخل الثابت لكي يقلل هاميلتوني إلى هاملتونيان الكلاسيكي في الحالات التي يُقرَّب فيها النظام الكمومي باستعمال النظام الكلاسيكي؛ وتسمى القدرة على إجراء مثل هذا التقريب في حدودٍ معينةٍ مبدأ التطابق.
يُعطى حل هذه المعادلة التفاضلية كما يأتي:
يُعرف عامل المؤثر باسم عامل النمو الزمني ولديه الخاصة الحاسمة بأنه وحدوي. يعتبر النمو الزمني هذا حتميًا بمعنى أنه -بالنظر إلى حالةٍ كموميةٍ أوليةٍ - يقدم تنبؤًا محددًا لماهية الحالة الكمية في أي وقت لاحق.[19]

من خلال دوال الموجة «المتزنة». على سبيل المثال يُصوَّر إلكترون واحد في ذرة غير مستثارةٍ تصويراً تقليدياً على هيئة جسيمٍ متحرِّكٍ في مسارٍ دائريٍّ حول النواة الذرية، بينما يجري وصفه في ميكانيكا الكم بواسطة دالة موجةٍ متزنةٍ تحيط بالنواة. مثلًا دالة الموجة الإلكترونية لذرة هيدروجينٍ غير مستثارةٍ هي دالة متناظرة كرويًا تُعرف باسم مدار s (الشكل 1).
تُعرف الحلول التحليلية لمعادلة شرودنغر بعددٍ قليلٍ جدًا من النماذج البسيطة نسبيًا من أتباع هاميلتونيين بما في ذلك الهزاز التوافقي الكمومي والجسيم في الصندوق وكاتيون ثنائي الهيدروجين وذرة الهيدروجين. حتى ذرة الهليوم -التي تحتوي على إلكترونين فقط- تحدت جميع المحاولات في علاجٍ تحليليٍّ كامل.
ومع هذا ثمة تقانات لإيجاد حلولٍ تقريبية. تستخدم إحدى الطرق -المسماة نظرية الاضطراب- النتيجة التحليلية لنموذجٍ ميكانيكيٍّ كميٍّ بسيطٍ لإنشاء نتيجةٍ لنموذجٍ ذي صلةٍ، ولكنه أكثر تعقيدًا -على سبيل المثال- عن طريق إضافة طاقةٍ كامنةٍ ضعيفة. هناك طريقة أخرى تسمى «معادلة الحركة شبه الكلاسيكية»، والتي تنطبق على الأنظمة التي ينتج عنها ميكانيكا الكم انحرافات صغيرة فقط عن السلوك الكلاسيكي. يمكن بعد ذلك حساب هذه الانحرافات بناءً على الحركة الكلاسيكية. هذا النهج مهم خصوصاً في حقل الفوضى الكمومية.
مبدأ اللايقين
إحدى النتائج الرئيسة للصيغ الكمومية هي مبدأ اللايقين. ينص هذا المبدأ في أكثر أشكاله شيوعًا على أنه لا يوجد تحضير لجسيمٍ كميٍّ يمكن أن يشير ضمنًا إلى تنبؤاتٍ دقيقةٍ في الوقت نفسه لتحديد موقعه وقياس زخمه.[20][21] كل من الموقع والزخم يمكن ملاحظتهما، مما يعني أنهما ممثَّلان من قبل المؤثرات الهيريميتية. مؤثر الموقع ومؤثر الزخم لا يستبدان بل يلبيان علاقة التبديل القانوني:
وبالنظر إلى الحالة الكمومية تتيح لنا قاعدة بورن حساب قيم التوقع لكل من و، بالإضافة إلى قوى كل منهما. تحديد اللايقين للملاحظة من خلال الانحراف المعياري، لدينا
وبالمثل بالنسبة للزخم:
ينص مبدأ اللايقين على ذلك
يمكن نظرياً أن يكون أي من الانحرافين المعياريين ذا قيمةٍ صغيرةٍ عشوائيًّا، ولكن ليس كلاهما في وقتٍ واحد.[22] تُعمَّم هذه المتباينة على أزواجٍ عشوائيةٍ من المؤثرات المترابطة ذاتيًا و. المبدل لهذين الموثرين هو
وهذا يوفر الحد الأدنى لجداء الانحرافات المعيارية:
ثمة نتيجة أخرى لعلاقة التبديل القانوني وهي أن مؤثري الموقع والزخم عبارة عن تحويلات فورييه لبعضهم بعضَا، فيكون وصف كائنٍ وفقًا لزخمه الخاص به هو تحويل فورييه لوصفه وفقًا لموقعه. وحقيقةً إن الاعتماد في الزخم هو تحويل فورييه للاعتماد في الموقع يعني أن مؤثر الزخم مكافئ (حتى عامل ) لأخذ المشتق وفقًا للموقع، لأن التمايز في تحليل فورييه يتوافق مع الضرب في الفضاء المزدوج، وهو السبب في المعادلات الكمومية في فضاء الموقع، يستبدل الزخم بـ، وعلى وجه الخصوص في معادلة شرودنغر غير النسبية في فضاء الموقع، يستبدل مصطلح مربع الزخم بضرب لابلاسيه .[20]
الأنظمة المركبة والتشابك
عندما ينظر إلى نظامين كموميين مختلفين معًا، فإن فضاء هيلبرت للنظام المدمج هو ناتج جداء الموتر لفضاءات هيلبرت للمكونين. مثلًا لنفترض أن A وB نظامان كموميان مع فضاءات هيلبرت و على التوالي. إذن فضاء هيلبرت للنظام المركب هو
إذا كانت حالة النظام الأول هي المتجه وكانت حالة النظام الثاني هي ، فإن حالة النظام المركب هي
لا يمكن كتابة جميع الحالات في فضاء هيلبرت المشترك بهذا الشكل، لأن مبدأ التراكب يشير إلى أن التوليفات الخطية لهذه الحالات «القابلة للفصل» أو «حالات المنتج» صالحة أيضًا. على سبيل المثال إذا كانت كلتا و حالتان ممكنتان للنظام وبالمثل و كلتاهما حالتان ممكنتان للنظام إذن
هي حالة مشتركة صالحة لا يمكن فصلها، والحالات غير القابلة للفصل تسمى متشابكة.[23][24]
إذا كانت حالة النظام المركب متشابكةً فمن المستحيل وصف أي نظام مكون A أو النظام B بواسطة متجه الحالة. يمكن للمرء بدلاً من ذلك تحديد مصفوفات الكثافة المنخفضة التي تصف الإحصائيات التي يمكن الحصول عليها من خلال إجراء قياساتٍ على أي نظامٍ مكونٍ بمفرده. يؤدي هذا بالضرورة إلى فقدان المعلومات، على الرغم من أن معرفة مصفوفات الكثافة المنخفضة للأنظمة الفردية لا يكفي لإعادة بناء حالة النظام المركب.[23][24] تمامًا كما تحدد مصفوفات الكثافة حالة نظامٍ فرعيٍّ لنظامٍ أكبر. بالمقابل تصف (POVMs) التأثير على نظام فرعي للقياس الذي يجري على نظام أكبر. تستخدم POVM على نطاق واسع في نظرية المعلومات الكمومية.[23][25]
وكما هو موضح أعلاه يعد التشابك سمة رئيسة لنماذج عمليات القياس التي تتشابك فيها الأدوات مع النظام الذي يجري قياسه. تتفاعل الأنظمة متشابكة مع البيئة حيث توجد، وهي ظاهرة تُعرف باسم إزالة الترابط الكمي. هذا يمكن أن يفسر لماذا -من الناحية العملية- تصعب ملاحظة التأثيرات الكمية في الأنظمة الأكبر من المجهرية.[26]
التكافؤ بين الصيغ
توجد صيغ عديدة متكافئة رياضيًا لوصف ميكانيكا الكم، أقدمها وأشهرها هي «نظرية التحويل» التي اقترحها بول ديراك، والتي توحد وتعمم الصيغتين الأقدم لميكانيكا الكم؛ ميكانيكا المصفوفة (وضعها فيرنر هايزنبيرغ) وميكانيكا الموجات (وضعها إرفين شرودنغر).[27] الصيغة البديلة لميكانيكا الكم هي صيغة فاينمان لتكامل المسار، وفيها يُنظر إلى السعة الميكانيكية الكمومية بوصفها مجموعاً للمسارات التقليدية وغير التقليدية الممكنة بين الوضعين الابتدائي والنهائي. هذا هو المقابل الميكانيكي الكمومي لمبدأ الفعل في الميكانيكا التقليدية.
التناظرات وقوانين الحفظ
يُعرف هاميلتونيان بأنه مُولِّد نمو الوقت، لأنه يحدد عامل النمو الزمني الوحدوي لكل قيمة من قيم . يترتب على هذه العلاقة بين و حفظ ويمكن ملاحظته أن توقُّع : لن يُغير القيمة بمرور الوقت. تُعمم هذه العبارة رياضيًا أي عامل هرميتي يمكن أن يولد مجموعةً من العوامل الوحدوية ذات معلماتٍ بواسطة متغير . في ظل التطور الناتج عن ، سيجري حفظ أي يمكن ملاحظته ويتنقل مع . علاوةً على ذلك إذا كان محفوظًا بالنمو تحت ، فإن يجري حفظه في ظل النمو الناتج عن . يشير هذا إلى نسخةٍ كميةٍ للنتيجة التي أثبتتها إيمي نويثر في الميكانيكا الكلاسيكية (لاغرانج): لكل تناظرٍ قابلٍ للاشتقاق الهاملتوني يوجد قانون حفظ مطابق.
أمثلة
جسيم حر

أبسط مثال على نظام كمي بدرجة حرية موقعية هو جسيم حر في بُعد مكاني واحد. الجسيم الحر هو الذي لا يخضع لتأثيرات خارجية، لذلك فإن الهاميلتوني يتكون فقط من طاقته الحركية:
يعطى الحل العام لمعادلة شرودنغر بواسطة
وهو تراكب لجميع الموجات المستوية الممكنة ، وهي حالات ذاتية لمؤثر الزخم مع الزخم . معاملات التراكب هي ، وهو تحويل فورييه للكم الأولي الحالة .
من غير الممكن أن يكون الحل عبارةً عن حالةٍ ذاتيةٍ واحدةٍ للزخم، أو حالةٍ ذاتيةٍ وحيدةِ الموقع، لأن هذه ليست حالاتٍ كموميةً قابلةً للتطبيع.[note 3] بدلاً من ذلك توصف حزمة الموجة الغاوسية كما يأتي:
ويُوصف توزيع الزخم بعد إنجاز تحويل فورييه
عندما يَتضاءل فإن الانتشار في الموقع يصبح أصغر، لكن انتشار الزخم يغدو أكبر. بالمقابل من خلال جعل أكبر، فإنّا نجعل الانتشار في الزخم أصغر، لكن الانتشار في الموقع يصبح أكبر، وهذا يوضح مبدأ اللايقين.
عندما ندع حزمة الموجة الغاوسية تنمو بمرور الوقت نرى أن مركزها يتحرك عبر الفضاء بسرعةٍ ثابتةٍ (مثل جسيم كلاسيكي دونما أي قوىً تؤثر عليه)، ومع ذلك فإن الحزمة الموجية ستنتشر أيضًا بتقدم الوقت، مما يعني أن الموقع يصبح غير مؤكدٍ أكثر فأكثر. ورغم ذلك فإن عدم اليقين في الزخم يظل ثابتًا.[28]
جسيم في صندوق

يعتبر الجسيم الموجود في صندوق طاقة كامنة (وضع) وحيد البعد هو المثال الأكثر بساطة من الناحية الحسابية وعندها تؤدي القيود إلى تكميم مستويات الطاقة. يُعرّف الصندوق بأنه لا يحتوي على طاقة كامنة في كل مكان داخل منطقة معينة، وبالتالي طاقة كامنة غير محدودة في كل مكان خارج تلك المنطقة.[20]:77–78 بالنسبة للحالة وحيدة البعد في اتجاه ، يمكن كتابة معادلة شرودنغر المستقلة عن الوقت
مع المؤثر التفاضلي المحدد بواسطة
المعادلة السابقة تستحضر نظير الطاقة الحركية الكلاسيكي،
مع الحالة في هذه الحالة تحتوي على طاقة تتطابق مع الطاقة الحركية للجسيم.
الحلول العامة لمعادلة شرودنغر للجسيم في الصندوق هي
أو، من صيغة أويلر،
تحدد الجدران المحتملة اللانهائية للمربع قيم و عند و وفيها يجب أن تكون صفرًا. وبالتالي، عند ،
و. عند ،
لا يمكن أن تكون تساوي صفرًا لأن هذا سيتعارض مع الافتراض بأن لها المعيار 1. لذلك، فإن ، يجب أن يكون عددًا صحيحًا مضاعفًا لـ،
هذا القيد على يعني قيدًا على مستويات الطاقة، مما ينتج عنه
إن بئر الجهد المحدود هو تعميم مشكلة بئر الجهد اللانهائي على الآبار الجهدية ذات العمق المحدود. مشكلة البئر المحدود هي أكثر تعقيدًا من الناحية الرياضية من مشكلة الجسيم اللانهائي في المربع لأن دالة الموجة ليست مثبتة على الصفر عند جدران البئر. بدلاً من ذلك، يجب أن تفي دالة الموجة بشروط حدودية رياضية أكثر تعقيدًا لأنها ليست صفرية في مناطق خارج البئر. مشكلة أخرى ذات صلة هي مشكلة حاجز الجهد المستطيل، الذي يقدم نموذجًا لتأثير النفق الكمي الذي يلعب دورًا مهمًا في أداء التقنيات الحديثة مثل ذاكرة الفلاش ومجهر المسح النفقي.
هزاز توافقي
كما في الحالة الكلاسيكية، تعطى طاقة وضع الاهتزاز التوافقي الكمومي بواسطة
يمكن معالجة هذه المشكلة إما عن طريق حل معادلة شرودنغر مباشرةً، وهي ليست بسيطة، أو باستخدام «طريقة السلم» الأكثر أناقة التي اقترحها بول ديراك لأول مرة. تعطى حالات ذاتية بواسطة
حيث Hn هي كثيرات حدود هيرامايت
ومستويات الطاقة المقابلة
هذا مثال آخر يوضح تقديرية الطاقة للحالات المقيدة.
مقياس التداخل ماخ زيندر

يوضح مقياس التداخل ماخ-زيندر (MZI) مفاهيم التراكب والتداخل مع الجبر الخطي في البعد 2، بدلاً من المعادلات التفاضلية. يمكن اعتبارها نسخة مبسطة من تجربة الشق المزدوج، لكنها ذات أهمية بحد ذاتها، على سبيل المثال في ممحاة الكم للاختيار المتأخر، واختبار قنبلة إليزور- فايدمان، وفي دراسات التشابك الكمي.[29][30]
يُنمذَج فوتون يمر عبر مقياس التداخل أخذاً بالحسبان وجود تراكب من مسارين فقط عند كل نقطة: المسار «الأسفل» الذي يبدأ من اليسار، ويمر مباشرة من خلال كل من مقسم الأشعة، وينتهي في الأعلى، والمسار «الأعلى» الذي يبدأ من الأسفل، ويمر مباشرة عبر مقسم الأشعة، وينتهي عند اليمين. وبالتالي فإن الحالة الكمومية للفوتون هي متجه وهو تراكب للمسار «الأسفل» والمسار «الأعلى» ، أي العقديان. من أجل احترام الافتراض بأن يتطلب ذلك .
صمم كلا مقسمي الأشعة على شكل المصفوفة الوحدوية ، مما يعني أنه عندما يلتقي الفوتون بمقسم الأشعة، فإنه إما سيبقى على المسار نفسه بسعة احتمالية تبلغ ، أو الانعكاس على المسار الآخر بسعة احتمالية تبلغ . صمم ناقل الطور في الجزء الأعلى من الذراع على شكل المصفوفة الوحدوية ، مما يعني أنه إذا كان الفوتون على المسار «الأعلى»، فسيحصل على طور نسبي من ، وسيبقى دون تغيير إذا كان في المسار الأسفل.
سيجري بعد ذلك العمل على الفوتون الذي يدخل مقياس التداخل من اليسار باستخدام مقسم الأشعة ، وناقل طور ، ومقسم أشعة آخر ، وهكذا ينتهي الأمر في الحالة
والاحتمالات التي سيجري اكتشافها على اليمين أو في الأعلى تعطى على التوالي بواسطة
لذلك يُستخدم مقياس التداخل ماخ زيندر لتقدير انزياح الطور من خلال تقدير هذه الاحتمالات.
ماذا يحدث لو كان الفوتون إما في المسار «الأسفل» أو «الأعلى» بين مقسم الأشعة؟ يمكن تحقيق ذلك عن طريق سد أحد المسارات، وأيضاً عن طريق إزالة مقسم الأشعة الأول (وتغذية الفوتون من اليسار أو من الأسفل، حسب الرغبة). في كلتا الحالتين لن يكون هناك تداخل بين المسارات بعد الآن، وتعطى الاحتمالات بواسطة ، بصرف النظر عن الطور . يعني هذا أن الفوتون لا يأخذ مسارًا أو آخر بعد مقسم الأشعة الأول، بل إنه في تراكب كمي حقيقي للمسارين.[31]
تطبيقات
نجحت ميكانيكا الكم نجاحًا هائلاً في شرح العديد من سمات الكون، خاصةً فيما يتعلق بالكميات الصغيرة والمنفصلة والتفاعلات التي لا يمكن تفسيرها بالطرق الكلاسيكية.[note 4] غالبًا ما تكون ميكانيكا الكم النظريةَ الوحيدةَ التي يمكن أن تكشف عن السلوكيات الفردية للجسيمات دون الذرية التي تكوّن أشكال المادة كلها (الإلكترونات والبروتونات والنيوترونات والفوتونات وغيرها). كما تعتمد فيزياء الحالة الصلبة وعلوم المواد على ميكانيكا الكم.[32]
تعمل التقانة الحديثة في العديد من الجوانب في النطاق الذي تكون فيه التأثيرات الكمية كبيرةً. تشمل التطبيقات المهمة لنظرية الكم كيمياء الكم، والبصريات الكمومية، والحوسبة الكمومية، والمغناطيسات فائقة التوصيل، والصمامات الثنائية الباعثة للضوء، والمضخم البصري والليزر، والترانزستور وأشباه الموصلات مثل المعالج الدقيق، والتصوير الطبي والبحثي مثل التصوير بالرنين المغناطيسي والمجهر الإلكتروني.[33] إن تفسير العديد من الظواهر الحيوية والفيزيائية متجذرة في طبيعة الرابطة الكيميائية، وأبرزها الحمض النووي للجزيء-الضخم.
علاقتها بالنظريات العلمية الأخرى
| جزء من سلسلة مقالات حول |
| الفيزياء الحديثة |
|---|
| |
| بوابة الفيزياء |
الميكانيكا الكلاسيكية
تؤكد قواعد ميكانيكا الكم أن فضاء حالة النظام هو فضاء هيلبرت، وأن ما يمكن ملاحظته في النظام هي مؤثرات هيرميتية تُطبَّق على المتجهات في ذلك الفضاء؛ على الرغم من أن هذه المتجهات لا تخبرنا عن فضاء هيلبرت أو المؤثرات. تُختار هذه أيضاً للحصول على وصفٍ كميٍّ للنظام الكمومي، وهي خطوة ضرورية لعمل تنبؤاتٍ فيزيائية. ثمة دليل مهم لاتخاذ هذه الاختيارات هو مبدأ التطابق، وهو دليل إرشادي ينص على أن تنبؤات ميكانيكا الكم تختزل إلى تلك الخاصة بالميكانيكا الكلاسيكية في نظام الأعداد الكمومية الكبيرة.[34] يمكن للمرء أيضًا أن يبدأ من نموذجٍ كلاسيكيٍّ راسخٍ لنظامٍ معين، ثم يحاول تخمين النموذج الكمومي الرئيس الذي من شأنه أن يؤدي إلى النموذج الكلاسيكي في حدود التطابق. يُعرف هذا النهج باسم التكميم.
عندما صيغت ميكانيكا الكم في الأصل طبقت على النماذج التي كان حد التطابق الخاص بها هو الميكانيكا الكلاسيكية غير النسبية. على سبيل المثال يُستخدم النموذج المعروف للهزاز التوافقي الكمومي تعبيرًا غيرَ نسبيٍّ صريحًا للطاقة الحركية للهزاز، وبالتالي فهو نسخة كمومية من الهزاز التوافقي الكلاسيكي.
تنشأ التعقيدات مع الأنظمة الفوضوية -التي لا تحتوي على أرقامٍ كميةٍ جيدةٍ- وتدرس الفوضى الكمومية العلاقة بين الأوصاف الكلاسيكية والكمومية في هذه الأنظمة.
إزالة الترابط الكمي هو آلية تفقد من خلالها الأنظمة الكمومية الاتساق، وبالتالي تصبح غير قادرة على عرض العديد من التأثيرات الكمومية النموذجية؛ إذ تصبح التراكبات الكمومية مجرد مزيج احتمالي، والتشابك الكمي يغدو ببساطة ارتباطات كلاسيكية. لا يتضح التماسك الكمي عادة على المقاييس العيانية -ربما باستثناء حالاتٍ عند درجات حرارةٍ تقترب من الصفر المطلق- والتي قد يظهر فيها السلوك الكمومي بمقاييسَ مجهرية.[note 5]
إن العديد من الخصائص العيانية للنظام الكلاسيكي هو نتيجة مباشرة للسلوك الكمومي لأجزائه. فعلى سبيل المثال إن استقرار المادة السائبة (المكوَّنة من الذرات والجزيئات التي تنهار بسرعةٍ تحت تأثير القوى الكهربائية وحدها)، وصلابة المواد الصلبة، والخصائص الميكانيكية والحرارية والكيميائية والبصرية والمغناطيسية للمادة؛ كلها قاطبةً إنْ هي إلا نتيجةٌ لتفاعل الشحنات الكهربائية بموجب قواعد ميكانيكا الكم.[35]
النسبية الخاصة والديناميكا الكهربائية
تضمنتِ المحاولات المبكرة لدمج ميكانيكا الكم مع النسبية الخاصة طرح معادلةٍ متغيرةٍ مثل معادلة كلاين-غوردون أو معادلة ديراك بديلاً عن معادلة شرودنغر. وفي حين كانت هذه النظريات ناجحةً في تفسير العديد من النتائج التجريبية، إلا أنها حوت بعض النقائص غير المُرْضيةِ النابعة من إهمالها للخلق النسبي وفناء الجسيمات. تتطلب نظرية الكم النسبية الكاملة في تطوير نظرية الحقل الكمومي، والتي تطبق التكميم على حقلٍ (بدلاً من مجموعةٍ ثابتةٍ من الجسيمات). توفر أول نظرية حقلٍ كميٍّ كاملٍ -وهي الكهروديناميكا الكمية- وصفًا كميًّا كاملًا للتفاعل الكهرومغناطيسي. تعد الكهروديناميكا الكمية لصيقةً إلى جانب النسبية العامة واحدةً من أكثر النظريات الفيزيائية دقةً على الإطلاق.[36][37]
وغالبًا ما تكون الأدوات الكاملة لنظرية الحقل الكمومي غير ضروريةٍ لوصف الأنظمة الكهروديناميكية. ثمة نهجٌ أبسطُ -هو النهج الذي استخدم منذ نشأة ميكانيكا الكم- وهو معالجة الجسيمات المشحونة كأجسامٍ ميكانيكيةٍ كموميةٍ يجري العمل عليها بواسطة مجال كهرومغناطيسي كلاسيكي. فمثلًا يصف النموذج الكمومي الأولي لذرة الهيدروجين الحقل الكهربائي لهذه الذرة باستخدام جهد كولوم تقليدي. يفشل هذا النهج «شبه الكلاسيكي» عندما يكون للتقلبات الكمومية في الحقل الكهرومغناطيسي دور مهم، مثل انبعاث الفوتونات بواسطة الجسيمات المشحونة.
طُورَت كذلك نظريات الحقل الكمومي للقوة النووية القوية والقوة النووية الضعيفة. تسمى نظرية الحقل الكمومي للقوة النووية القوية بالديناميكا اللونية الكمومية، وتصف تفاعلات الجسيمات دون النووية مثل الكواركات والغلوونات. جرى توحيد القوة النووية الضعيفة والقوة الكهرومغناطيسية في أشكالهما الكمومية في نظرية حقلٍ كميٍّ واحدٍ (تُعرف باسم نظرية الكهروضعيفة) بواسطة كل من: محمد عبد السلام وشيلدون جلاشو وستيفن واينبرج.[38]
العلاقة مع النسبية العامة
على الرغم من أن تنبؤات كلٍّ من نظرية الكم والنسبية العامة كانت مدعومةً بأدلةٍ تجريبيةٍ صارمةٍ ومتكررةٍ، إلا أن شكلياتها المجردة تتعارض بعضها مع بعضٍ بحيث ثبت أن من الصعب للغاية دمجها في نموذجٍ واحدٍ متّسقٍ ومتماسك. لما كانتِ الجاذبية تكاد لاتذكر في العديد من مجالات فيزياء الجسيمات، فإن التوحيد بين النسبية العامة وميكانيكا الكم لم يك قضيةً ملحةً في تلك التطبيقات الخاصة. ومع ذلك يعد الافتقار إلى نظريةٍ صحيحةٍ للجاذبية الكمومية قضيةً لها اعتبارها في علم الكون الفيزيائي. لقد بحث الفيزيائيون عن «نظرية كل شيء» (TOE) أنيقة. وعليه كان حل التناقضات بين النظريتين هدفًا رئيسيًا لفيزياء القرنين العشرين والحادي والعشرين. كان على نظرية كل شيء (TOE) لا أن تجمع نماذج الفيزياء دون الذرية فحسب، ولكن أيضًا قضية اشتقاق القوى الأربعة الرئيسة في الطبيعة انطلاقًا من قوةٍ أو ظاهرةٍ واحدة.[39]
تقترح نظرية الأوتار تفسيراً مستبدلةً بالجسيمات الشبيهة بالنقاط في فيزياء الجسيمات أجساماً وحيدة البعد تسمى الأوتار. تصف هذه االنظرية كيف تنتشر هذه الأوتار عبر الفضاء وتتفاعل مع بعضها بعضًا. يبدو الوتر -على مسافاتٍ أكبر من مقاس الوتر- تمامًا مثل الجسيم العادي، بكتلته وشحنته وخصائص أخرى تحددها حالة اهتزاز الوتر. في نظرية الأوتار تتوافق إحدى حالات الاهتزازات العديدة للسلسلة مع الجرافتون، وهو جسيم ميكانيكي كمومي يحمل قوة الجاذبية.[40][41]
والنظرية الشائعة الأخرى هي الجاذبية الكمية الحلقية (LQG) -والتي تصف الخصائص الكمومية للجاذبية- وعليه فهي نظرية الزمكان الكمومي. إن الجاذبية الكمية الحلقية (LQG) ما هي إلا محاولة لدمج وتكييف ميكانيكا الكم القياسية والنسبية العامة القياسية. تصف هذه النظرية الفضاء بأنه نسيج ناعم للغاية «منسوج» من حلقاتٍ محدودةٍ تسمى شبكاتٍ مغزلية. يسمى تطور الشبكة المغزلية بمرور الوقت الرغوة المغزلية، ومقياس الطول المميز للرغوة المغزلية هو طول بلانك، أي قرابة 1.616×10−35 متر، وبناءً عليه فإن الأطوال الأقصر من طول بلانك ليست ذات معنىً ماديٍّ في الجاذبية الكمية الحلقية (LQG).[42]
الآثار الفلسفية
أثارت ميكانيكا الكم منذ نشأتها نقاشاتٍ فلسفيةً متنوعةً، وطُوِّر لها العديد من التفسيرات. تركز الحجج على الطبيعة الاحتمالية لميكانيكا الكم، والصعوبات المتعلقة بانهيار الدالة الموجية، ومسألة القياس الكمي ذات الصلة، والكم غير الموضعي. ولريما كان الاتفاق الوحيد في هذه المسائل هو غياب الإجماع العلمي حول أيِّ منها. قال ريتشارد فاينمان ذات مرةٍ: «أعتقد أنني أستطيع القول بثقةٍ إنه لا أحد يفهم ميكانيكا الكم.»[43] أما ستيفن واينبرج فأعرب: «لا يوجد الآن في رأيي تفسير مرضٍ تمامًا لميكانيكا الكم.»[44]
تُجمَع آراء نيلز بور وفيرنر هايزنبيرغ والفيزيائيين الآخرين في الغالب معًا تحت مسمى «تفسير كوبنهاغن».[45][46] ووفقًا لهذه الآراء مجتمعةً فإن الطبيعة الاحتمالية لميكانيكا الكم ليست سمةً مؤقتةً سيستبدل بها -في نهاية المطاف- نظرية حتمية، ولكنها تشكل بدلاً من ذلك التخلي النهائي عن الفكرة الكلاسيكية «السببية». لقد أكد نيلز بور -على الخصوص- أن أي تطبيقٍ محددٍ جيدًا للشكلية الميكانيكية الكمية يجب أن يشير دائمًا إلى الترتيب التجريبي، بسبب الطبيعة التكاملية للأدلة التي يُحصل عليها في ظل مواقفَ تجريبيةٍ مختلفة. ظلتِ التفسيرات من نمط [مدرسة] كوبنهاغن شائعةً حتى في القرن الحادي والعشرين.[47]
كان ألبرت أينشتاين -أحد مؤسسي نظرية الكم القديمة- ممتعضًا من فشلها الواضح في احترام بعض المبادئ الميتافيزيقية العزيزة، مثل الحتمية والمحلية. تُعرف حوارات أينشتاين المديدة مع نيلز بور حول ماهية ميكانيكا الكم وحالتها باسم مناظرات بور-أينشتاين. رأى أينشتاين أن على ميكانيكا الكم أن تكون نظريةً تحظر صراحةً الفعل عن بعد، وجادل بأن ميكانيكا الكم غيرُ مكتملةٍ، وهو رأي كان صحيحاً ولكنه غيرُ جوهريٍّ ومماثلٌ لكيفية صحة الديناميكا الحرارية، لكن النظرية الأساس الكامنة وراءها هي الميكانيكا الإحصائية. وفي عام 1935 نشر أينشتاين ومعاونوه بوريس بودولسكي وناثان روزين حجةً مفادها أن مبدأ المكان يعني عدم اكتمال ميكانيكا الكم، وهي تجربة فكرية أطلق عليها فيما بعد مفارقة أينشتاين-بودولسكي-روزين (حجة EPR).[note 6] عام 1964 أظهر جون بل -فيما يُعرف الآن باسم مبرهنة بل (أو عدم مساواة بل)- أن مبدأ (EPR) الخاص بالمكان -مقرونًا مع الحتمية- كان في الواقع غير متوافقٍ مع ميكانيكا الكم؛ فقد تضمن قيودًا على الارتباطات التي تنتجها أنظمة البعد، والتي يمكن للجسيمات المتشابكة أن تنتهكها.[52] مذ ذاك الحين أجري العديد من التجارب للوصول إلى هذه الارتباطات، وكان مُؤدى نتيجة هذه التجارب أنها تنتهك في الواقع عدم مساواة بل، وبالتالي زيف اقتران المكان بالحتمية.[14][15]
تُظهِر ميكانيكا بوم إمكانية إعادة صياغة ميكانيكا الكم بهدف جعلها حتميةً، ولكن -وبصريح العبارة- على حساب جعلها غير محليةٍ. لا تنتسب الدالة الموجية إلى نظامٍ ماديٍّ فحسب، بل تنسب أيضًا موقعًا حقيقيًا يتطور تطوراً قطعيًّا بموجب معادلةٍ توجيهيةٍ غير محلية. يجري تقديم تطور النظام الفيزيائي في جميع الأوقات من خلال معادلة شرودنغر مقرونةً مع المعادلة التوجيهية؛ لا يوجد أبدًا انهيار للدالة الموجية، وهذا -بدوره أيضًا- يحل معضلة القياس.[53]
يرى تفسير إيفرت للعوالم المتعددة -الذي صيغ في عام 1956- أن الاحتمالات التي وصفتها نظرية الكم تحدث كلُّها متزامنةً في وقتٍ واحدٍ في كونٍ متعددٍ يتألف على الأرجح من أكوانٍ متوازيةٍ مستقلة.[54] ينتج هذا من إزالة بدهيّة انهيار الحزمة الموجية. إن جميع الحالات الممكنة للنظام المَقيس وجهاز القياس -جنبًا إلى جنبٍ مع المراقب- موجودة في تراكب كمي حقيقي. ونحن ندرك السلوكَ غيرَ الحتمي -الذي تحكمه الاحتمالات- في حين إن الكون متعدد [الأكوان] حتمي، وماذاك إلا لأننا لا نلاحظ الكون المتعدد ككل، ولكن كونًا واحدًا موازيًا فقط في كل مرة. كانتِ الطريقة التي يُفترض أن يعمل بها هذا الكون موضوعًا بالضبط لكثيرٍ من الجدل، وقد بُذلت محاولات عدة لفهم هذا واستنباط قاعدة بورن -من ثَمَّ-[55][56] دونما إجماعٍ حول ما إذا كانت تلك القاعدة ناجحةً أم لا.[note 7][58][59]
ظهرت ميكانيكا الكم العلائقية في أواخر التسعينيات مشتقاً حديثاً لأفكارٍ من نمط [مدرسة] كوبنهاغن،[60] وجرى تطوير ميكانيكا بيشان الكمية (أو اختصارًا QBism) بعد بضع سنوات.[61]
تاريخ

طُوِّرت ميكانيكا الكم في العقود الأولى من القرن العشرين مدفوعةً بالحاجة إلى تفسير الظواهر التي لوحظت في بعض الحالات في أوقاتٍ سابقة. بدأ البحث العلمي في الطبيعة الموجية للضوء في القرنين السابع عشر والثامن عشر، عندما اقترح علماء مثل روبرت هوك وكريستيان هوغنس وليونهارت أويلر النظرية الموجية للضوء بناءً على الملاحظات التجريبية.[62] وفي عام 1803 وصف الموسوعي الإنجليزي توماس يانغ تجربة الشق المزدوج الشهيرة،[63] الني لعبت دورًا رئيسيًا في القبول العام للنظرية الموجية للضوء.
ثمَّن البحث الكيميائي لجون دالتون وأميديو أفوجادرو للنظرية الذرية للمادة في أوائل القرن التاسع عشر، وهي فكرة بنى عليها جيمس كليرك ماكسويل ولودفيغ بولتزمان وآخرون لتأسيس النظرية الحركية للغازات، وقد أعطت نجاحات هذه النظرية مزيدًا من المصداقية لفكرة أن المادة تتكون من ذراتٍ، ومع ذلك كانت للنظرية أيضًا أوجه قصور لا يمكن حلها إلا من خلال تطوير ميكانيكا الكم.[64] في حين كان المفهوم المبكر للذرات منذ الفلسفة اليونانية أنها وحدات غير قابلة للتجزئة (كلمة «ذرة» مشتقة من اليونانية بمعنى «غير قابلة للتجزئة») شهد القرن التاسع عشر صياغة فرضياتٍ حول التركيب دون الذري، وكان أحد الاكتشافات المهمة في هذا الصدد هو ملاحظة مايكل فاراداي عام 1838 لتوهجٍ ناجمٍ عن تفريغٍ كهربائيٍّ داخل أنبوبٍ زجاجيٍّ يحتوي على غازٍ عند ضغطٍ منخفض. واصل يوليوس بلوكر ويوهان فيلهلم هيتورف ويوجين غولدشتاين عمل فاراداي وحسنوه، ثم وُصِفت الأشعة المهبطية، والتي وجد جوزيف جون طومسون أنها تتكون من جسيماتٍ دون ذريةٍ تسمى إلكترونات.[65][66]
اكتشف غوستاف كيرشهوف مشكلة إشعاع الجسم الأسود في عام 1859. وفي عام 1900 اقترح ماكس بلانك فرضية أن الطاقة تُشع وتُمتص على شكل «كوانتا» منفصلة (أو حزم طاقة) ينتج عنه حساب يطابق بدقةٍ الأنماط المرصودة لإشعاع الجسم الأسود.[67] كلمة «كم» مشتقة من اللاتينية، وتعني «كم هو عظيم» أو «كم الثمن».[68] تُقسَّم كميات الطاقة وفقًا لبلانك إلى «عناصرَ» يتناسب مقدارها (E) مع ترددها (ν):
- ،
وفيها h هو ثابت بلانك. أصر بلانك بحذرٍ على أن هذا ليس إلا جانبًا من جوانب عمليات امتصاص الإشعاع وانبعاثه وبأنه مغاير للواقع المادي للإشعاع.[69] في الواقع اعتبرت فرضيته "المبدأ الكمي" خدعةً رياضيةً للوصول إلى الإجابة الصحيحة بدلاً من اكتشافٍ كبير.[70] ومع ذلك ففي عام 1905 فسر ألبرت أينشتاين فرضية بلانك الكمومية تفسيرًا واقعيًّا، واستخدمها لشرح التأثير الكهروضوئي، وفيها يمكن للضوء الساطع على موادَّ معينةٍ أن يسبب قذف الإلكترونات من المادة. ثم طور نيلز بور أفكار بلانك حول الإشعاع إلى نموذج بور لذرة الهيدروجين والذي تنبأ بنجاحٍ بالخطوط الطيفية للهيدروجين.[71] طور أينشتاين هذه الفكرة أيضًا لإظهار أن الموجة الكهرومغناطيسية مثل الضوء يمكن أيضًا أن توصف بأنها جسيمات (سميت فيما بعد بالفوتونات) مع كميةٍ منفصلةٍ من الطاقة تعتمد على ترددها.[72] وفي ورقته البحثية «حول نظرية الكم للإشعاع» توسع أينشتاين في قضية التفاعل بين الطاقة والمادة لشرح امتصاص الطاقة وانبعاثها بواسطة الذرات. وعلى الرغم من أن نظريته النسبية العامة طغت على بحثه هذا في ذلك الوقت، إلا أنه أوضح الآلية الكامنة وراء الانبعاث المحفز للإشعاع،[73] والذي أصبح مبدأ الليزر.

تُعرف هذه المرحلة بنظرية الكم القديمة، والتي لم تكن مكتملةً أو متسقةً مع ذاتها، بل عبارةً عن مجموعةٍ من التصحيحات التجريبية للميكانيكا الكلاسيكية.[74] تُفهم النظرية الآن على أنها تقريب شبه كلاسيكي[75] لميكانيكا الكم الحديثة.[76] تشمل النتائج الملحوظة من تلك الفترة بالإضافة إلى أعمال بلانك وأينشتاين وبور المذكورة أعلاه، عمل أينشتاين وبيتر ديباي حول الحرارة النوعية للمواد الصلبة وبرهان نيلز بور وهندريكا جوانا فان ليوين على أن الفيزياء الكلاسيكية لا يمكن أن تفسر المغناطيسية المعاكسة، وتوسيع أرنولد سومرفيلد لنموذج بور ليشمل التأثيرات النسبية الخاصة.
أصبحت ميكانيكا الكم الصيغة القياسية المستعملة لوصف الفيزياء الذرية بحلول العشرينيات من القرن الماضي. طرح الفيزيائي الفرنسي لويس دي بروي نظريته عن موجات المادة في عام 1923 قائلًا إن الجسيمات يمكن أن تظهر خصائص الموجة والعكس بالعكس. وفقاً لمنهج دي بروي فقد وُلدت ميكانيكا الكم الحديثة في عام 1925 عندما طور الفيزيائيون الألمان فيرنر هايزنبيرغ وماكس بورن وباسكوال جوردان[77][78] ميكانيكا المصفوفة ووضع الفيزيائي النمساوي إرفين شرودنغر ميكانيكا الموجات. قدم بورن التفسير الاحتمالي لوظيفة شرودنغر الموجية في يوليو 1926.[79] وهكذا ظهر مجال فيزياء الكم بأكمله، مما أدى إلى قبوله على نطاق واسع في مؤتمر سولفاي الخامس عام 1927.[80]
وحَّد ديفيد هيلبرت وبول ديراك وجون فون نيومان ميكانيكا الكم[81] بحلول عام 1930 وأضفَوا عليها الطابع الرسمي مع التركيز تركيزاً أكبر على القياس والطبيعة الإحصائية لمعرفتنا بالواقع والتكهنات الفلسفية حول "المراقب". ومنذ ذلك الحين تغلغلت في العديد من التخصصات، بما في ذلك كيمياء الكم، والإلكترونيات الكمومية، والبصريات الكمومية، وعلم المعلومات الكمومية، كما يوفر إطارًا مفيدًا للعديد من ميزات الجدول الدوري الحديث للعناصر، ويصف سلوك الذرات أثناء الترابط الكيميائي وتدفق الإلكترونات في أشباه الموصلات الحاسوبية، وبذا يلعب دورًا حاسمًا في العديد من التقانات الحديثة. وبينما أنشئت ميكانيكا الكم لوصف عالم الأشياء بالغة الصغر، إلا أنها ضرورية أيضًا لشرح بعض الظواهر العيانية مثل الموصلات الفائقة[note 8] والموائع الفائقة.[83]
انظر أيضًا
هوامش
- ^ انظر على سبيل المثال اختبارات الدقة للكهروديناميكا الكمية. لقد ثبت أن التنقيح النسبي لميكانيكا الكم المعروف باسم الكهروديناميكا الكمية (QED) يتفق مع التجربة في حدود جزءٍ واحدٍ من كل 108 لبعض الخصائص الذرية.
- ^ يحذر الفيزيائي جون سي بايز، "لا توجد طريقة لفهم تفسير ميكانيكا الكم دون القدرة أيضًا على حل مسائل ميكانيكا الكم؛ لفهم النظرية يجب أن تكون قادرًا على استخدامها (والعكس صحيح)".[16] أوجز كارل ساغان "الأساس الرياضي" لميكانيكا الكم وكتب: "بالنسبة لمعظم طلاب الفيزياء قد يشغلهم هذا من الصف الثالث -مثلاً- إلى مرحلة الدراسات العليا؛ ما يقرب من 15 عامًا.[...] إن مهمة مُبسِّط العلم -ذاك الذي يحاول إيصال فكرةٍ عن ميكانيكا الكم إلى الجمهور العام ممّن لم يعايش شعائر البدء هذه من قبل- لَهيَ مهمة شاقة. ولهذا السبب -جزئيًا- لا توجد في الواقع تبسيطات ناجحة لميكانيكا الكم في رأيي".[17]
- ^ إن الحالة ذاتية الزخم ستكون موجةً وحيدة اللون تمامًا ذات مدىً لانهائي، وهي ليست مربعة التكامل. وبالمثل فإن موقع الحالة الذاتية سيكون توزيع دلتا ديراك، وليس قابلًا للتكامل المربع، وليس من الناحية الفنية دالة على الإطلاق. وبالتالي لا يمكن أن ينتمي أي منهما إلى فضاء هلبرت للجسيم. يقدم الفيزيائيون أحيانًا "قواعدَ" وهميةً لفضاء هلبرت تشتمل على عناصرَ من خارج ذلك الفضاء جرى اختراعها من أجل التبسيط الحسابي ولا تمثل الحالات المادية.[20]:100–105
- ^ انظر -على سبيل المثال- محاضرات فاينمان في الفيزياء لبعض التطبيقات التكنولوجية التي تستخدم ميكانيكا الكم، مثلًا الترانزستور (المجلد III، الصفحات 11-14 وما يليها)، الدوائر المتكاملة، وهي تقانة تابعة لفيزياء الحالة الصلبة (المجلد II، الصفحات 6-8)، والليزر (المجلد III، ص 9-13).
- ^ انظر الظواهر الكمومية العيانية، تكاثف بوز-أينشتاين، والآلة كمومية.
- ^ يرجع الشكل المنشور من حجة EPR إلى بودولسكي، ولم يكن أينشتاين نفسه راضيًا عنها. استخدم أينشتاين في منشوراته ومراسلاته حجةً مختلفةً للإصرار على أن ميكانيكا الكم نظرية غير مكتملة.[48][49][50][51]
- ^ يبدو الاستنتاج بأننا لم نحصل على أي اشتقاقٍ لقاعدة بورن استنتاجٌ مقبولٌ -بشكلٍ عامٍ- حتى الآن، ولكن هذا لا يعني أن مثل هذا الاشتقاق مستحيل من حيث المبدأ.[57]
- ^ ...كان يعتقد منذ فترة طويلة أن الدالة الموجية لمعادلة شرودنغر لن يكون لها أبدًا تمثيل عياني مشابه للتمثيل العياني لسعة الفوتونات. من ناحية أخرى أدرك الآن أن ظاهرة الموصلية الفائقة تقدم لنا هذا الموقف فقط.[82]
المراجع
- ^ Born, M. (1926). "Zur Quantenmechanik der Stoßvorgänge" [On the Quantum Mechanics of Collision Processes]. Zeitschrift für Physik (بEnglish). 37 (12): 863–867. Bibcode:1926ZPhy...37..863B. DOI:10.1007/BF01397477. S2CID:119896026.
- ^ أ ب ت Feynman, Richard; Leighton, Robert; Sands, Matthew (1964). The Feynman Lectures on Physics (بEnglish). California Institute of Technology. Vol. 3. p. 1.1. ISBN:978-0201500646. Archived from the original on 2023-06-07. Retrieved 2020-12-19.
- ^ Jaeger, Gregg (2014). "What in the (quantum) world is macroscopic?". American Journal of Physics (بEnglish). 82 (9): 896–905. Bibcode:2014AmJPh..82..896J. DOI:10.1119/1.4878358.
- ^ Nobel Foundation. "The Nobel Prize in Physics 1921" (بEnglish). Archived from the original on 2022-09-30. Retrieved 2020-11-07.
- ^ Yaakov Y. Fein؛ Philipp Geyer؛ Patrick Zwick؛ Filip Kiałka؛ Sebastian Pedalino؛ Marcel Mayor؛ Stefan Gerlich؛ Markus Arndt (2019). "Quantum superposition of molecules beyond 25 kDa". Nature Physics. ج. 15 ع. 12: 1242–1245. Bibcode:2019NatPh..15.1242F. DOI:10.1038/s41567-019-0663-9. S2CID:203638258.
- ^ Bojowald, Martin (2015). "Quantum cosmology: a review". Reports on Progress in Physics (بEnglish). 78 (2): 023901. arXiv:1501.04899. Bibcode:2015RPPh...78b3901B. DOI:10.1088/0034-4885/78/2/023901. PMID:25582917. S2CID:18463042.
- ^ أ ب ت Lederman, Leon M.; Hill, Christopher T. (2011). Quantum Physics for Poets (بEnglish). US: Prometheus Books. ISBN:978-1616142810. Archived from the original on 2022-09-22.
- ^ Müller-Kirsten, H. J. W. (2006). Introduction to Quantum Mechanics: Schrödinger Equation and Path Integral (بEnglish). US: World Scientific. p. 14. ISBN:978-981-2566911. Archived from the original on 2022-10-11.
- ^ Plotnitsky, Arkady (2012). Niels Bohr and Complementarity: An Introduction (بEnglish). US: Springer. pp. 75–76. ISBN:978-1461445173. Archived from the original on 2022-10-09.
- ^ Griffiths, David J. (1995). Introduction to Quantum Mechanics (بEnglish). Prentice Hall. ISBN:0-13-124405-1.
- ^ Trixler, F. (2013). "Quantum tunnelling to the origin and evolution of life". Current Organic Chemistry (بEnglish). 17 (16): 1758–1770. DOI:10.2174/13852728113179990083. PMC:3768233. PMID:24039543.
- ^ Bub, Jeffrey (2019). "Quantum entanglement". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy (بEnglish). Metaphysics Research Lab, Stanford University.
- ^ أ ب Caves, Carlton M. (2015). "Quantum Information Science: Emerging No More". In Kelley, Paul; Agrawal, Govind; Bass, Mike; Hecht, Jeff; Stroud, Carlos (eds.). OSA Century of Optics (بEnglish). Optical Society of America. pp. 320–323. arXiv:1302.1864. Bibcode:2013arXiv1302.1864C. ISBN:978-1-943580-04-0.
- ^ أ ب Wiseman, Howard (2015). "Death by experiment for local realism". Nature (بEnglish). 526 (7575): 649–650. DOI:10.1038/nature15631. ISSN:0028-0836. PMID:26503054.
- ^ أ ب Wolchover, Natalie (7 Feb 2017). "Experiment Reaffirms Quantum Weirdness". Quanta Magazine (بEnglish). Archived from the original on 2022-05-26. Retrieved 2020-02-08.
- ^ Baez, John C. (2020). "How to Learn Math and Physics". University of California, Riverside (بEnglish). Archived from the original on 2022-11-12. Retrieved 2020-12-19.
- ^ Sagan, Carl (1996). The Demon-Haunted World: Science as a Candle in the Dark (بEnglish). Ballantine Books. p. 249. ISBN:0-345-40946-9.
- ^ Greenstein, George; Zajonc, Arthur (2006). The Quantum Challenge: Modern Research on the Foundations of Quantum Mechanics (بEnglish) (2nd ed.). Jones and Bartlett Publishers, Inc. p. 215. ISBN:978-0-7637-2470-2. Archived from the original on 2023-03-07., Chapter 8, p. 215
- ^ Weinberg, Steven (2010). Dreams Of A Final Theory: The Search for The Fundamental Laws of Nature (بEnglish). Random House. p. 82. ISBN:978-1-4070-6396-6. Archived from the original on 2022-08-25.
- ^ أ ب ت ث Cohen-Tannoudji, Claude; Diu, Bernard; Laloë, Franck (2005). Quantum Mechanics (بEnglish). Translated by Hemley, Susan Reid; Ostrowsky, Nicole; Ostrowsky, Dan. John Wiley & Sons. ISBN:0-471-16433-X.
- ^ Landau, L.D.; Lifschitz, E.M. (1977). Quantum Mechanics: Non-Relativistic Theory (بEnglish) (3rd ed.). Pergamon Press. Vol. 3. ISBN:978-0-08-020940-1. OCLC:2284121. Archived from the original on 2022-05-14.
- ^ Section 3.2 of Ballentine, Leslie E. (1970), "The Statistical Interpretation of Quantum Mechanics", Reviews of Modern Physics (بEnglish), vol. 42, pp. 358–381, Bibcode:1970RvMP...42..358B, DOI:10.1103/RevModPhys.42.358, S2CID:120024263. This fact is experimentally well-known for example in quantum optics; see e.g. chap. 2 and Fig. 2.1 Leonhardt، Ulf (1997)، Measuring the Quantum State of Light، Cambridge: Cambridge University Press، ISBN:0-521-49730-2، مؤرشف من الأصل في 2021-12-13
- ^ أ ب ت Nielsen, Michael A.; Chuang, Isaac L. (2010). Quantum Computation and Quantum Information (بEnglish) (2nd ed.). Cambridge: Cambridge University Press. ISBN:978-1-107-00217-3. OCLC:844974180.
- ^ أ ب Rieffel, Eleanor G.; Polak, Wolfgang H. (2011). Quantum Computing: A Gentle Introduction (بEnglish). MIT Press. ISBN:978-0-262-01506-6.
- ^ Wilde, Mark M. (2017). Quantum Information Theory (بEnglish) (2nd ed.). Cambridge University Press. arXiv:1106.1445. DOI:10.1017/9781316809976.001. ISBN:9781107176164. OCLC:973404322. S2CID:2515538.
- ^ Schlosshauer, Maximilian (2019). "Quantum decoherence". Physics Reports (بEnglish). 831: 1–57. arXiv:1911.06282. Bibcode:2019PhR...831....1S. DOI:10.1016/j.physrep.2019.10.001. S2CID:208006050.
- ^ Rechenberg, Helmut (1987). "Erwin Schrödinger and the creation of wave mechanics". Acta Physica Polonica B (بEnglish). 19 (8): 683–695. Archived from the original (PDF) on 2022-01-18. Retrieved 2016-06-13.
- ^ Mathews، Piravonu Mathews؛ Venkatesan، K. (1976). "The Schrödinger Equation and Stationary States". A Textbook of Quantum Mechanics. Tata McGraw-Hill. ص. 36. ISBN:978-0-07-096510-2.
- ^ Paris, M. G. A. (1999). "Entanglement and visibility at the output of a Mach–Zehnder interferometer". Physical Review A (بEnglish). 59 (2): 1615–1621. arXiv:quant-ph/9811078. Bibcode:1999PhRvA..59.1615P. DOI:10.1103/PhysRevA.59.1615. S2CID:13963928.
- ^ Haack, G. R.; Förster, H.; Büttiker, M. (2010). "Parity detection and entanglement with a Mach-Zehnder interferometer". Physical Review B (بEnglish). 82 (15): 155303. arXiv:1005.3976. Bibcode:2010PhRvB..82o5303H. DOI:10.1103/PhysRevB.82.155303. S2CID:119261326.
- ^ Vedral, Vlatko (2006). Introduction to Quantum Information Science (بEnglish). Oxford University Press. ISBN:9780199215706. OCLC:442351498.
- ^ Cohen, Marvin L. (2008). "Essay: Fifty Years of Condensed Matter Physics". Physical Review Letters (بEnglish). 101 (25): 250001. Bibcode:2008PhRvL.101y0001C. DOI:10.1103/PhysRevLett.101.250001. PMID:19113681. Archived from the original on 2022-08-19. Retrieved 2012-03-31.
- ^ Matson, John. "What Is Quantum Mechanics Good for?". Scientific American (بEnglish). Archived from the original on 2022-03-27. Retrieved 2016-05-18.
- ^ Tipler, Paul; Llewellyn, Ralph (2008). Modern Physics (بEnglish) (5th ed.). W.H. Freeman and Company. pp. 160–161. ISBN:978-0-7167-7550-8.
- ^ "Atomic Properties" (بEnglish). Academic.brooklyn.cuny.edu. Archived from the original on 2022-11-09. Retrieved 2012-08-18.
- ^ Hawking, Stephen; Penrose, Roger (2010). The Nature of Space and Time (بEnglish). ISBN:978-1400834747. Archived from the original on 2022-04-07.
- ^ Tatsumi Aoyama; Masashi Hayakawa; Toichiro Kinoshita; Makiko Nio (2012). "Tenth-Order QED Contribution to the Electron g-2 and an Improved Value of the Fine Structure Constant". Physical Review Letters (بEnglish). 109 (11): 111807. arXiv:1205.5368. Bibcode:2012PhRvL.109k1807A. DOI:10.1103/PhysRevLett.109.111807. PMID:23005618. S2CID:14712017.
- ^ "The Nobel Prize in Physics 1979" (بEnglish). Nobel Foundation. Archived from the original on 2022-11-10. Retrieved 2020-12-16.
- ^ Overbye, Dennis (2022). "Black Holes May Hide a Mind-Bending Secret About Our Universe - Take gravity, add quantum mechanics, stir. What do you get? Just maybe, a holographic cosmos". The New York Times (بEnglish). Archived from the original on 2022-11-16. Retrieved 2022-10-10.
- ^ Becker, Katrin; Becker, Melanie; Schwarz, John (2007). String theory and M-theory: A modern introduction (بEnglish). Cambridge University Press. ISBN:978-0-521-86069-7.
- ^ Zwiebach, Barton (2009). A First Course in String Theory (بEnglish). Cambridge University Press. ISBN:978-0-521-88032-9.
- ^ Rovelli, Carlo; Vidotto, Francesca (2014). Covariant Loop Quantum Gravity: An Elementary Introduction to Quantum Gravity and Spinfoam Theory (بEnglish). Cambridge University Press. ISBN:978-1-316-14811-2. Archived from the original on 2022-01-18.
- ^ Feynman, Richard (1967). The Character of Physical Law (بEnglish). MIT Press. p. 129. ISBN:0-262-56003-8.
- ^ Weinberg، Steven (2012). "Collapse of the state vector". Physical Review A. ج. 85 ع. 6: 062116. arXiv:1109.6462. Bibcode:2012PhRvA..85f2116W. DOI:10.1103/PhysRevA.85.062116. S2CID:119273840.
- ^ Howard, Don (2004). "Who Invented the 'Copenhagen Interpretation'? A Study in Mythology". Philosophy of Science (بEnglish). 71 (5): 669–682. DOI:10.1086/425941. ISSN:0031-8248. S2CID:9454552. Archived from the original on 2022-01-18.
- ^ Camilleri, Kristian (2009). "Constructing the Myth of the Copenhagen Interpretation". Perspectives on Science (بEnglish). 17 (1): 26–57. DOI:10.1162/posc.2009.17.1.26. ISSN:1063-6145. S2CID:57559199. Archived from the original on 2022-11-13.
- ^ Schlosshauer, Maximilian; Kofler, Johannes; Zeilinger, Anton (2013). "A snapshot of foundational attitudes toward quantum mechanics". Studies in History and Philosophy of Science Part B (بEnglish). 44 (3): 222–230. arXiv:1301.1069. Bibcode:2013SHPMP..44..222S. DOI:10.1016/j.shpsb.2013.04.004. S2CID:55537196.
- ^ Harrigan, Nicholas; Spekkens, Robert W. (2010). "Einstein, incompleteness, and the epistemic view of quantum states". Foundations of Physics (بEnglish). 40 (2): 125. arXiv:0706.2661. Bibcode:2010FoPh...40..125H. DOI:10.1007/s10701-009-9347-0. S2CID:32755624.
- ^ Howard, D. (1985). "Einstein on locality and separability". Studies in History and Philosophy of Science Part A (بEnglish). 16 (3): 171–201. Bibcode:1985SHPSA..16..171H. DOI:10.1016/0039-3681(85)90001-9.
- ^ Sauer, Tilman (2007). "An Einstein manuscript on the EPR paradox for spin observables". Studies in History and Philosophy of Science Part B: Studies in History and Philosophy of Modern Physics (بEnglish). 38 (4): 879–887. Bibcode:2007SHPMP..38..879S. CiteSeerX:10.1.1.571.6089. DOI:10.1016/j.shpsb.2007.03.002. ISSN:1355-2198. Archived from the original on 2022-11-13.
- ^ Einstein, Albert (1949). "Autobiographical Notes". In Schilpp, Paul Arthur (ed.). Albert Einstein: Philosopher-Scientist (بEnglish). Open Court Publishing Company.
- ^ Bell, J. S. (1964). "On the Einstein Podolsky Rosen paradox". Physics Physique Fizika (بEnglish). 1 (3): 195–200. DOI:10.1103/PhysicsPhysiqueFizika.1.195.
- ^ Goldstein, Sheldon (2017). "Bohmian Mechanics". Stanford Encyclopedia of Philosophy (بEnglish). Metaphysics Research Lab, Stanford University.
- ^ Barrett, Jeffrey (2018). "Everett's Relative-State Formulation of Quantum Mechanics". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy (بEnglish). Metaphysics Research Lab, Stanford University.
- ^ Everett, Hugh; Wheeler, J. A.; DeWitt, B. S.; Cooper, L. N.; Van Vechten, D.; Graham, N. (1973). DeWitt, Bryce; Graham, R. Neill (eds.). The Many-Worlds Interpretation of Quantum Mechanics. Princeton Series in Physics (بEnglish). Princeton, NJ: Princeton University Press. p. v. ISBN:0-691-08131-X.
- ^ Wallace, David (2003). "Everettian Rationality: defending Deutsch's approach to probability in the Everett interpretation". Stud. Hist. Phil. Mod. Phys. (بEnglish). 34 (3): 415–438. arXiv:quant-ph/0303050. Bibcode:2003SHPMP..34..415W. DOI:10.1016/S1355-2198(03)00036-4. S2CID:1921913.
- ^ Landsman, N. P. (2008). "The Born rule and its interpretation" (PDF). In Weinert, F.; Hentschel, K.; Greenberger, D.; Falkenburg, B. (eds.). Compendium of Quantum Physics (بEnglish). Springer. ISBN:978-3-540-70622-9.
- ^ Ballentine, L. E. (1973). "Can the statistical postulate of quantum theory be derived? – A critique of the many-universes interpretation". Foundations of Physics (بEnglish). 3 (2): 229–240. Bibcode:1973FoPh....3..229B. DOI:10.1007/BF00708440. S2CID:121747282.
- ^ Kent, Adrian (2010). "One world versus many: The inadequacy of Everettian accounts of evolution, probability, and scientific confirmation". In S. Saunders; J. Barrett; A. Kent; D. Wallace (eds.). Many Worlds? Everett, Quantum Theory and Reality (بEnglish). Oxford University Press. arXiv:0905.0624. Bibcode:2009arXiv0905.0624K.
- ^ Van Fraassen, Bas C. (2010). "Rovelli's World". Foundations of Physics (بEnglish). 40 (4): 390–417. Bibcode:2010FoPh...40..390V. DOI:10.1007/s10701-009-9326-5. ISSN:0015-9018. S2CID:17217776. Archived from the original on 2022-10-07.
- ^ Healey, Richard (2016). "Quantum-Bayesian and Pragmatist Views of Quantum Theory". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy (بEnglish). Metaphysics Research Lab, Stanford University.
- ^ Born, Max; Wolf, Emil (1999). Principles of Optics (بEnglish). Cambridge University Press. ISBN:0-521-64222-1. OCLC:1151058062.
- ^ Scheider, Walter (1986). "Bringing one of the great moments of science to the classroom". The Physics Teacher (بEnglish). 24 (4): 217–219. Bibcode:1986PhTea..24..217S. DOI:10.1119/1.2341987. ISSN:0031-921X. Archived from the original on 2022-07-30.
- ^ Feynman, Richard; Leighton, Robert; Sands, Matthew (1964). The Feynman Lectures on Physics (بEnglish). California Institute of Technology. Vol. 1. ISBN:978-0201500646. Archived from the original on 2023-06-07. Retrieved 2021-09-30.
- ^ Martin, Andre (1986), "Cathode Ray Tubes for Industrial and Military Applications", In Hawkes, Peter (ed.), Advances in Electronics and Electron Physics, Volume 67 (بEnglish), Academic Press, p. 183, ISBN:978-0080577333,
Evidence for the existence of "cathode-rays" was first found by Plücker and Hittorf ...
- ^ Dahl, Per F. (1997). Flash of the Cathode Rays: A History of J J Thomson's Electron (بEnglish). CRC Press. pp. 47–57. ISBN:978-0-7503-0453-5. Archived from the original on 2022-10-07.
- ^ Mehra, J.; Rechenberg, H. (1982). The Historical Development of Quantum Theory, Vol. 1: The Quantum Theory of Planck, Einstein, Bohr and Sommerfeld. Its Foundation and the Rise of Its Difficulties (1900–1925) (بEnglish). New York: Springer-Verlag. ISBN:978-0387906423.
- ^ "Quantum – Definition and More from the Free Merriam-Webster Dictionary" (بEnglish). Merriam-webster.com. Archived from the original on 2022-11-10. Retrieved 2012-08-18.
- ^ Kuhn, T. S. (1978). Black-body theory and the quantum discontinuity 1894–1912 (بEnglish). Oxford: Clarendon Press. ISBN:978-0195023831.
- ^ Kragh, Helge (2000). "Max Planck: the reluctant revolutionary". Physics World (بEnglish). Archived from the original on 2022-11-14. Retrieved 2020-12-12.
- ^ Stachel, John (2009). "Bohr and the Photon". Quantum Reality, Relativistic Causality and the Closing of the Epistemic Circle. The Western Ontario Series in Philosophy of Science (بEnglish). Dordrecht: Springer. Vol. 73. pp. 69–83. DOI:10.1007/978-1-4020-9107-0_5. ISBN:978-1-4020-9106-3.
- ^ Einstein, A. (1905). "Über einen die Erzeugung und Verwandlung des Lichtes betreffenden heuristischen Gesichtspunkt" [On a heuristic point of view concerning the production and transformation of light]. Annalen der Physik (بEnglish). 17 (6): 132–148. Bibcode:1905AnP...322..132E. DOI:10.1002/andp.19053220607. Reprinted in Stachel, John, ed. (1989). The Collected Papers of Albert Einstein (بDeutsch). Princeton University Press. Vol. 2. pp. 149–166. See also "Einstein's early work on the quantum hypothesis", ibid. pp. 134–148.
- ^ Einstein, Albert (1917). "Zur Quantentheorie der Strahlung" [On the Quantum Theory of Radiation]. Physikalische Zeitschrift (بDeutsch). 18: 121–128. Bibcode:1917PhyZ...18..121E. Translated in Einstein, A. (1967). "On the Quantum Theory of Radiation". The Old Quantum Theory (بEnglish). Elsevier. pp. 167–183. DOI:10.1016/b978-0-08-012102-4.50018-8. ISBN:978-0080121024.
- ^ ter Haar, D. (1967). The Old Quantum Theory (بEnglish). Pergamon Press. pp. 206. ISBN:978-0-08-012101-7. Archived from the original on 2020-06-10.
- ^ "Semi-classical approximation". Encyclopedia of Mathematics (بEnglish). Archived from the original on 2022-10-07. Retrieved 2020-02-01.
- ^ Sakurai, J. J.; Napolitano, J. (2014). "Quantum Dynamics". Modern Quantum Mechanics (بEnglish). Pearson. ISBN:978-1-292-02410-3. OCLC:929609283.
- ^ David Edwards,"The Mathematical Foundations of Quantum Mechanics", Synthese, Volume 42, Number 1/September, 1979, pp. 1–70.
- ^ D. Edwards, "The Mathematical Foundations of Quantum Field Theory: Fermions, Gauge Fields, and Super-symmetry, Part I: Lattice Field Theories", International J. of Theor. Phys., Vol. 20, No. 7 (1981).
- ^ Bernstein, Jeremy (2005). "Max Born and the quantum theory". American Journal of Physics (بEnglish). 73 (11): 999–1008. Bibcode:2005AmJPh..73..999B. DOI:10.1119/1.2060717. ISSN:0002-9505.
- ^ Pais, Abraham (1997). A Tale of Two Continents: A Physicist's Life in a Turbulent World (بEnglish). Princeton, New Jersey: Princeton University Press. ISBN:0-691-01243-1. Archived from the original on 2021-08-19.
- ^ Van Hove, Leon (1958). "Von Neumann's contributions to quantum mechanics" (PDF). Bulletin of the American Mathematical Society (بEnglish). 64 (3): Part 2:95–99. DOI:10.1090/s0002-9904-1958-10206-2. Archived from the original (PDF) on 2022-11-09.
- ^ Feynman, Richard. "The Feynman Lectures on Physics III 21-4" (بEnglish). California Institute of Technology. Archived from the original on 2023-06-07. Retrieved 2015-11-24.
- ^ Packard, Richard (2006). "Berkeley Experiments on Superfluid Macroscopic Quantum Effects" (PDF) (بEnglish). Archived from the original (PDF) on 2015-11-25. Retrieved 2015-11-24.
مراجع عربية
- ^ Q115526796، ص. 248، QID:Q115526796
- ^ Q113987323، ص. 236، QID:Q113987323
- ^ Q113016239، ص. 378، QID:Q113016239
- ^ تعريف مصطلح «فيقياء» في المعجم البصري على موقع ديوان اللغة العربية. (تاريخ الاطلاع: 10 يونيو 2020) "نسخة مؤرشفة". مؤرشف من الأصل في 2020-10-20. اطلع عليه بتاريخ 2020-06-11.
{{استشهاد ويب}}: صيانة الاستشهاد: BOT: original URL status unknown (link)
وصلات خارجية
| ميكانيكا الكم في المشاريع الشقيقة: | |
- خمسة كتب تشرح لك ميكانيكا الكم بسهولة، موقع الجزيرة. (بالعربية)
- ما هي ميكانيكا الكم؟ تفسير ميكانيكا الكم وتبسيطها، مبادرة أنا أصدق العلم. (بالعربية)
- مقالات عن ميكانيكا الكم، مبادرة ناسا بالعربي. (بالعربية)
- كتب ميكانيكا الكم للمبتدئين، موقع الفيزياء.كوم. (بالعربية)
- سلسلة ميكانيكا الكم، على اليوتيوب. (بالعربية)