|
تضامنًا مع حق الشعب الفلسطيني |
زخم الحركة
زخم الحركة |
| الميكانيكا الكلاسيكية |
|---|
| تاريخ الميكانيكا الكلاسيكية |
| بوابة الفيزياء |
الزخم[1] أو زخم الحركة[2] أو كمية الحركة[3] هو أحد الكميات الفيزيائية التي عرفت من خلال الفيزياء الكلاسيكية بأنها حاصل ضرب كتلة الجسم في سرعته، ينطبق على كمية الحركة أحد مبادئ الانحفاظ في الفيزياء الكلاسيكية وهو مبدأ حفظ الزخم أو قانون حفظ الزخم.
ووحدات كمية الحركة أو زخم الحركة هي : كيلوجرام.متر/ثانية.
الميكانيكا النيوتونية
يتحدد الزخم بمقدار واتجاه. تعرف هذه الكميات التي لها مقدار واتجاه باسم كميات متجهة. من هذه الخاصية يمكن أن نتنبأ باتجاه الأجسام بعد التصادم بالإضافة إلى سرعتها. يمكن وصف خواص الزخم في اتجاه واحد وبعد واحد. تشبه الكميات الاتجاهية معادلات الكميات القياسية.
جسم واحد
يمكننا التعبير عن الزخم لجسم بالحرف p وهو حاصل ضرب الكتلة والسرعة.[4]
- وحدات الزخم هي حاصل ضرب وحدة الكتلة والسرعة. بالوحدات الدولية فإن وحدة الكتلة هي الكيلو جرام والسرعة هي المتر لكل ثانية وبذلك تكون وحدة كمية التحرك هي كجم متر لكل ثانية. في نظام وحدات السنتيميتر جرام ثانية فإن وحدة الكتلة هي الجرام والسرعة هي سنتيمتر لكل ثانية لذلك تكون وحدة كمية التحرك هي جرام سنتيميتر لكل ثانية.
كونها اتجاهيه فإنه على سبيل المثال هناك نموذج لطائرة كتلتها 1 كجم تتحرك بسرعة 1 متر لكل ثانية في اتجاه الشمال لذلك فأن كمية التحرك هي 1 كجم متر لكل ثانية باتجاه الشمال.
حفظ كمية الحركة

يظل الزخم في النظام المغلق ( حيث لا تُتبادل المادة مع الوسط المحيط ولا يتأثر بأي قوى خارجية) ثابتاً. هذه الحقيقة وهي مبدأ الحفاظ على كمية الحركة مفهوم ضمني من قوانين نيوتن للحركة. بفرض أن هناك جسمين متفاعلين مع بعضهما وبتطبيق القانون الثالت لنيوتن فإن القوى بينهما تكون متساوية ومتضادة في الاتجاه. إذا كان الجسمين هما 1 و 2 فإن F تساوي:
F1 = dp1dt و F2 = dp2dt.
وبذلك فإن:
الإشارة السالبة تعني أن القوتين في اتجاهين متضادين.
إذا كانت سرعة الجسمين قبل التصادم هما u1 و u2 وسرعتهم بعد التصادم هي v1 و v2 فإن:
وبالتشابه فإنه إذا وجد أجسام عديدة فإن الزخم المتبادل بين كل جسمين يكون صفر وبالتالي يكون التغير الكلي للزخم صفر. يمكننا تطبيق هذا القانون على جميع التصادمات وعمليات الفصل الناجمة بالقوة. يمكن استخدامه أيضا في المواقف التي لا تُطبق قوانين نيوتن فيها مثل نظرية النسبية.
أجسام متعددة
كمية التحرك لمجموعة أجسام هي مجموع الأزخام لهم جميعا. إذا كان لدينا جسمين لهم كتلة و و سرعة كل جسم و فإن الزخم لهم يكون
يمكن حساب الزخم لأكثر من جسمين من العلاقة:
يمكن حساب مركز ثقل لمجموعة أجسام من خلال العلاقة:
إذا كانت جميع الأجسام تتحرك فإن مركز الثقل لهم جميعا يتحرك أيضا. إذا كان مركز الثقل يتحرك بسرعة vcm فإن كمية الحركة تكون:
هذا يمكن تعريفه بقانون أويلر الأول.[5][6]
علاقة مع القوة
عند التأثير بقوة مقدارها F لزمن قدره Δt فإن الزخم يتغير بمقدار يساوي:
يسمي هذا القانون بقانون نيوتن الثاني، يتناسب معدل التغير في الزخم بمقدار القوة المؤثرة على الجسم.
إذا كانت القوة تعتمد على الزمن وتتغير خلال الفترة من t1 و t2 ، فإن التغير في الزخم يكون:
- عند فرض أن الكتلة ثابتة فإن القوة تساوي:
لذلك فإن القوة تساوي حاصل ضرب الكتلة في العجلة.
مثال: نموذج طائرة له كتلة تساوي 1 كجم وتصل من السكون إلى سرعة 6 متر لكل ثانية في خلال ثانيتين باتجاه الشمال. القوة التي نحتاجها للوصول لهذا التسارع هي 3 نيوتن في اتجاه الشمال. قيمة التغير في الزخم تساوي 6 كجم متر لكل ثانية.
في الميكانيكا الكلاسيكية
في الميكانيكا الكلاسيكية، كمية الحركة (الزّخم) لجسيم كتلته ذو سرعة ، تعرّف على أنّها حاصل ضرب الكتلة في السرعة:
وحدة قياس الزخم طبقاً للنظام الدولي: كغ.م/ثا، يجب أن لا يخلط بينها وبين وحدة نيوتن لقياس القوة التي تعتبر حاصل ضرب للكتلة في التسارع (أو العجلة).
كمية الحركة والدفع
يعرف الدفع (impulse) على أنه مقدار التغير من زخم الجسم المدفوع وتكتب كالآتي:
حيث
- تعني الدفع
ومن المعادلة السابقة بقسمة طرفيها وضربهما في نحصل على المعادلة التالية:
حيث F القوة، Δt التغير في الزمن
الزخم طبقا للنظرية النسبية الخاصة
تعطي الميكانيكا الكلاسيكية طبقا لنيوتن العلاقة بين طاقة حركة الجسم و الزخم والكتلة بالعلاقة:
حيث:
p زخم الجسم، m الكتلة النقطوية من الجسم.
وطبقا للنظرية النسبية الخاصة لأينشتاين لا تتزايد زخم الجسم تزايدا طرديا بتزايد سرعته حيث لاتتزايد سرعته طبقا لعلاقة خطية وإنما تحدها سرعة الضوء كحدأقصي، وتُعطي النظرية النسبية زخم الجسم بالعلاقة:
حيث:
m كتلة السكون للجسم، v سرعة الجسم.
كما تعطي العلاقة بين طاقة حركة الجسم وكتلته بالعلاقة :
أما بالنسبة للفوتون وهو عديم الكتلة ويتحرك باستمرار بسرعة الضوء ولا يوجد في حالة سكون، في هذه الحالة تعطينا نظرية الكم زخم الفوتون بالعلاقة:
الاعتماد على المرجع
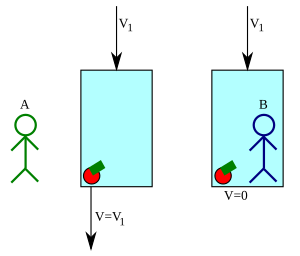
كمية الحركة هي كمية قياسية وتعتمد قيمتها على حركة الملاحظ. على سبيل المثال، عند وجود تفاحة داخل حوض زجاجي تتحرك لأسفل فإن وجود ملاحظ خارج هذا الزجاج يجد أن كمية الحركة لها لا تساوي صفر بينما إذا وجد داخله فإنه يجد ان التفاحة لا تتحرك وبالتالي كمية الحركة لها تساوي صفر.
نفرض أن هناك جسيم له موضع x في إطار مرجعي، عند النظر إليه من إطار آخر يتحرك بسرعة u فإن موضع الجسيم يتغير مع الزمن:
يمكن تسمية هذا يتحويل جاليليو. إذا كان الجسيم يتحرك بسرعة dxdt = v في المرجع الأول فإن في الثاني يتحرك بسرعة:
وبما أن u لا تتغير فإن العجلة تكون نفسها.
إن التغيير في الإطار المرجعي يمكنه فقط من تيسير عمل الحسابات. على سبيل المثال، عند تصادم جسمين فإنه يمكن اختيار إطار مرجعي حيث يبدأ أحد الجسمين عنده من الصفر. يمكن اختيار إطار مرجعي آخر يستخدم كثيرا وهو إطار مركز الثقل الذي يتحرك مع مركز ثقل الجسم وتكون عنده كمية الحركة تساوي صفر.
تطبيقات على التصادم
إن قانون بقاء كمية التحرك غير كاف لتحديد حركة الجسيم بعد التصادم. يجب أن نعرف خاصية أخرى وهي طاقة الحركة للجسيم. هذه الطاقة ليست بالضرورة تظل ثابتة بعد التصادم. إذا ظلت ثابتة هذه الطاقة فيكون التصادم مرن وإذا لم تحفظ فيكون غير مرن.
التصادمات المرنة

في التصادمات المرنة ليس هناك فقد في طاقة الحركة. في التصادم المرن التام لا يكون هناك احتكاك بين الأجسام مثلما يحدث بين الذرات حيث يكون هناك تنافر كهربي بينهم. تصادم بين كرتين مائيتين هو مثال آخر للتصام المرن التام ولكن بالتأكيد عندما يحدث احتكاك بين جسمين فلا بد من وجود تبدد لبعض الطاقة.[7]
إذا كانت سرعة الجسمين المتصادمين قبل التصادم u1 و u2 وسرعة هذه الاجسام بعد التصادم v1 و v2 فإن المعادلات التي تعبر عن مبدأ حفظ الطاقة وطاقة الحركة هي:
يمكن تحليل التصادم بصورة مبسطة من خلال تغيير الإطار المرجعي. على سبيل المثال نفرض أن هناك جسمين لهما كتلة واحدة m أحدها ثابتة والأخرى تتحرك في اتجاهه بسرعة v. يتحرك مركز الثقل بسرعة v2 ويتحرك كلا الجسمين تجاهه بسرعة v2 . بعد تصادم الجسيمن، يجب أن يتحرك كلاهما بسرعات متساوية وفي اتجاهات متضادة. بإضافة سرعة مركز الثقل لكلاهما نجد أن الجسم الذي كان متحرك من قبل قد توقف بينما الجسم الساكن يتحرك بسرعة v. الأجسام هنا تبادلت السرعات. السرعات النهائية يمكن حسابها من:
عند معرفة السرعة الابتدائية فيمكننا معرفة السرعة النهائية للأجسام [8]
إذا كان أحد الجسمين له كتلة أكبر فإن فإن سرعته ستتأثر قليلا بسبب التصادم بينما الآخر سيطرأ عليه تغير كبير.
تصادم غير مرن

يتحول جزأ طاقة الحركة للاجسام المتصادمة في التصادم الغير مرن إلى أشكال أخرى من الطاقات مثل الحرارة والصوت. يمكن رؤيه هذه الطاقة المفقودة في التلف الحادث للمركبة.
في التصادم الغير مرن التام فإن كلا الجسمين يكون لهما نفس الحركة بعد التصادم. مبدأ بقاء كمية الحركة هو:
لذلك:
عندما يكون الإطار المرجعي متحرك بسرعة v فإن الاجسام المتصادمة تسكن وتقف عن الحركة وتتبدد طاقة الحركة جميعها.
من العوامل التي تبين التصادم الغير مرن هو معامل الرد وهو النسبة بين السرعة النسبية للفصل للسرعة النسبية للتقارب. عند تطبيق هذا لكرة الرياضة فإننا يمكن قياسه من العلاقة:[9]
يمكن تطبيق معادلات كمية التحرك والطاقة للاجسام المتحركة سويا والتي تبعد عن بعضها بعد ذلك على سبيل المثال، الانفجارات التي تنتج عن سلسلة تفاعلات التي تحول طاقة الوضع المخزنة في صورة كيميائية، ميكانيكية أو نووية إلى طاقة حركية، صوتية وإشعاع كهرومغناطيسي.
انظر أيضًا
مراجع
- ^ Q111421033، ص. 87، QID:Q111421033
- ^ قاموس المورد، البعلبكي، بيروت، لبنان.
- ^ ميشال إبراهيم ورامي أبو سليمان وفادي (1 يناير 2007). Dictionaire des termes scientifiques (Anglais/Français/Arabe): قاموس المصطلحات العلمية - انكليزي/فرنسي/عربي. Dar Al Kotob Al Ilmiyah دار الكتب العلمية. ISBN:978-2-7451-5445-3. مؤرشف من الأصل في 2020-05-12.
- ^ Feynman Vol. 1، Chapter 9
- ^ "Euler's Laws of Motion". مؤرشف من الأصل في 2018-10-02. اطلع عليه بتاريخ 2009-03-30.
- ^ McGill and King (1995). Engineering Mechanics, An Introduction to Dynamics (ط. 3rd). PWS Publishing Company. ISBN:0-534-93399-8.
- ^ Carl Nave (2010). "Elastic and inelastic collisions". Hyperphysics. مؤرشف من الأصل في 2018-10-04. اطلع عليه بتاريخ 2012-08-02.
- ^ Serway، Raymond A.؛ John W. Jewett, Jr (2012). Principles of physics : a calculus-based text (ط. 5th). Boston, MA: Brooks/Cole, Cengage Learning. ص. 245. ISBN:9781133104261.
- ^ McGinnis، Peter M. (2005). Biomechanics of sport and exercise (ط. 2nd). Champaign, IL [u.a.]: Human Kinetics. ص. 85. ISBN:9780736051019. مؤرشف من الأصل في 2017-04-06.
| في كومنز صور وملفات عن: زخم الحركة |