|
تضامنًا مع حق الشعب الفلسطيني |
قوة محصلة
| الميكانيكا الكلاسيكية |
|---|
| تاريخ الميكانيكا الكلاسيكية |
| بوابة الفيزياء |
القوة المحصلة هي قوة فردية و معها عزم الدوران نُتجت عن طريق نظام مركب من قوي وعزوم تؤثر علي جسم جاسئ. القوة المحصلة تكون مساوية في القيمة مجموع القوي الأصلية المؤثرة.[1]
تحد نقطة التأثير للقوة المحصلة مقدار عزم الدوران المترابط مه هذة القوة.
توضيح
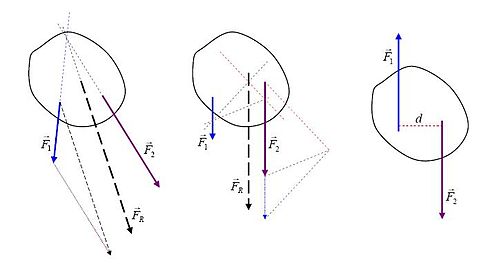
يوضح الشكل ببساطة الطرق البيانية كيفية تحديد خط عمل القوة المحصلة لأنظمة بسيطة من القوة.
- خطوط عمل القوي الأساسية و تتقابل. بعد حدوث جمع جبري في مكان قوة ، محصلة هذة القوي تتكون بحيث نقطة تأثيرها تمر في نقطة التقاء القوي الأساسية، وبالتالي جميع العزوم تساوي صفر، فتصبح القوة المحصلة تساوي مجموع العزوم للقوي الأصلية.
- الشكل الأوسط يوضح قوتان متوازيان، بعد جمع جبري عند مكان قوة ، القوة المحصلة تنتقل إلي نقطة تأثير محددة. تعتمد هذة العملية علي تحليل جميع القوي إلي مركبات بحيث جميع خطوط عمل هذة القوي تتقابل عند نقطة واحدة.
- يوضح الشكل الأيمن ازدواج، قوتان متساويتان ولكن عكس اتجاه وبالتالي تصبح القوة المحصلة تساوي صفر، ولكن يحدث ازدواج ، حيث هي المسافة بين خطان عمل هاتان القوتان.
متجه موجه
تؤثر أي قوي في نقطة تأثير، وهذا التأثير يختلف باختلاف مكانها. لهذا السبب أي قوة تكون متجه موجه. تُجمع القوي التي تكون في نفس الاتجاه، ولكن تُطرح القوي التي تكون عكس الاتجاه. ببساطة يُمكن تغيير نقطة تأثير أي قوة بإدخال قوي متساوية و عكس الاتجاه عند نقاط تأثير مختلفه، وبالتالي يحدث ازدواج صافي علي الجسم.
ازدواج
نقطة R هي نقطة تأثير القوة المحصلة F لنظام ما عليه n عدد من القوي Fi و معها ازدواج T :
و .
نقطة التأثير R في أي مكان علي خط عمل F مع حدوث اختلاف لقيمة الازدواج، وبالتالي:
القوة المحصلة حرة الازدواج
نقطة التأثير R هي التقطة التي عندها يكون الازدواج يساوي صفر.
حيث F القوة المحصلة، وFi هي القوي الأصلية علي نظام ما.
إذا تم تحقيق هذا الشرط بالأعلي بالتالي هناك نقطة يكون لديها قوة صافية من غير ازدواج.
مراجع
- ^ H. Dadourian, Analytical Mechanics for Students of Physics and Engineering, Van Nostrand Co., Boston, MA 1913 نسخة محفوظة 4 مارس 2020 على موقع واي باك مشين.