|
تضامنًا مع حق الشعب الفلسطيني |
تأثير كوريوليس

تأثير كوريوليس في الفيزياء، يطلق اسم تأثير كوريوليس على التشوه الظاهري في حركة الأجسام، عندما ينظر إليها (عندما ترصد) من إطار مرجعي دوراني.[1][2][3]
أطلق هذا الاسم على ذكر غاسبارد-غوستاف كوريوليس، العالم الفرنسي الذي وصف هذا التشوه الظاهري في عام 1835، مع أن الرياضيات التي ظهرت في المعادلات المدية من قبل بيير-سيمون لابلاس منذ عام 1778. يحدث تأثير كوريوليس نتيجة ما يدعى بقوة كوريوليس، التي تظهر في معادلة الحركة لجسم ما ضمن إطار مرجعي دوراني. قوة كوريوليس تعتبر مثالا عن القوى التخيلية fictitious force، لأنها لا تظهر عندما يتم التعبير عن نفس الحركة ضمن إطار مرجعي عطالي، حيث يتم شرح حركة الجسم عن طريق القوى الحقيقية المطبقة دون الحاجة لقوة تخيلية، طبعا مع مفهوم العطالة. أما في إطار مرجعي دوراني، فإن قوى كوريوليس تعتمد على السرعة للجسم المتحرك، والقوة النابذة، التي لاتعتمد على سرعة الأجسام المتحركة. كلا القوتين لازمتين لوصف الحركة بشكل دقيق.
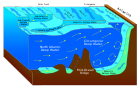
ربما تكون الإطار المرجعي الدوراني الأكثر أهمية هو الأرض. فالأجسام المتحركة بحرية على سطح الأرض تتعرض لقوة كوريوليس، ويظهر ذلك في ميلان حركتها نحو اليمين في نصف الكرة الشمالي، ونحو اليسار في نصف الكرة الجنوبي. حركة الهواء والرياح في الغلاف الأرضي والمياه في المحيطات هي أمثلة واضحة لهذا السلوك. فبدلا من التوجه مباشرة من مناطق الضغط المرتفع لمناطق الضغط المنخفض كما يجب أن يحدث في كوكب غير دائر، نجد أن اتجاه الحركة ينحرف قليلا إلى اليمين من منطقة الضغط المنخفض في النصف الشمالي، وبالعكس إلى اليسار في النصف الجنوبي.
نظرة تاريخية
وصف العالم الإيطالي «جيوفاني باتيستا ريتشيولي» ومساعده «فرانشيسكو ماريا جريمالدي» التأثير وعلاقته بسلاح المدفعية في 1651 في كتاب المجسطي الجديد، إذ كتبا أن دوران الأرض سيسبب انحرافاً شرقياً للقذائق المُطلقة نحو الشمال.[4] في عام 1674، وصف «كلود فرانسوا ميليت ديكالز» في كتاب منهاج عالم الرياضيات كيف أن دوران الأرض يسبب انحراف مسارات الأجسام الساقطة والمقذوفات المُوجهة إلى أحد قطبي الكوكب. وصف كل من ريتشيولي وجريمالدي وديكالز التأثير كجزء من حجتهم ضد نظام مركزية الشمس الذي اقترحه « كوبرنيكوس». بعبارة أخرى، جادلوا بأن دوران الأرض يجب أن ينتج هذا التأثير، وبالتالي فقد كان الفشل في كشفه دليلاً على ثبات الأرض. اشتُقت معادلة تسارع كوريوليس من قبل «أويلر» في عام 1749،[5][6] ووُصف التأثير في معادلات المد والجزر الخاصة بـ «بيير سيمون لابلاس» في عام 1778.[7]
نشر غاسبارد جوستاف كوريوليس بحثاً في عام 1835 حول الطاقة الناتجة عن الآلات ذات الأجزاء الدوارة، مثل نواعير الماء.[8] شمل البحث القوى التكميلية المرصودة في الإطار المرجعي الدوراني. قسم كوريوليس هذه القوى التكميلية إلى فئتين. شملت الفئة الثانية القوة الناشئة عن الضرب الاتجاهي بين السرعة الزاوية لنظام الإحداثيات وإسقاط متجه سرعة الجسم في مستوى عمودي على محور دوران النظام. أشار كوريوليس إلى هذه القوة باسم «قوة الطرد المركزي المركبة» بسبب تشابهها مع قوة الطرد المركزي التي شملتها الفئة الأولى.[9][10] كان التأثير معروفًا في أوائل القرن العشرين باسم «تسارع كوريوليس»، وباسم «قوة كوريوليس» بحلول عام 1920.[11]
في عام 1856، اقترح «وليام فيريل» وجود منطقة دوران على خطوط العرض الوسطى حيث تحرف قوة كوريوليس الهواء لتوليد رياح الغربيات السائدة.[12]
كان فهم الحركة المجردة لتأثير دوران الأرض على تدفق الهواء جزئيًا في البداية.[13] في أواخر القرن التاسع عشر، فُهم المدى الكامل للتفاعل واسع النطاق بين قوة تدرج الضغط والقوة الحارفة التي تؤدي في النهاية إلى تحرك الكتل الهوائية على طول خطوط تساوي الضغط.[14]
الأسباب
لا تظهر قوة كوريوليس إلا عند استخدام إطار مرجعي دوراني. في الإطار الدوراني، تتصرف هذه القوة تمامًا مثل القوى الحقيقية (أي تُسبب تسارع الأجسام ولها تأثيرات حقيقية).[15] مع ذلك، تنتج قوة كوريوليس عن القصور الذاتي، ولا تُعزى إلى مصادر يمكن التعرف عليها، مثلما هو الحال مع القوة الكهرومغناطيسية أو النووية، على سبيل المثال. من وجهة نظر تحليلية، لاستخدام قانون نيوتن الثاني في نظام دوراني، من الضروري تضمين قوة كوريوليس رياضياً، لكنها تختفي في الإطار المرجعي القصوري غير المتسارع. على سبيل المثال، تخيل طفلين يلعبان على جانبين مقابلين من دوامة الخيل، ويرميان كرةً إلى بعضهما البعض. من وجهة نظر الطفلين، تتبع الكرة مساراً منحنياً نتيجة قوة كوريوليس. افترض أن الدوامة تدور عكس اتجاه عقارب الساعة عند النظر من الأعلى. من منظور رامي الكرة، تنحرف الكرة إلى اليمين. من منظور الطفل الآخر، تنحرف الكرة إلى اليسار. في علم الأرصاد الجوية، يوفر الإطار الدوراني (الأرض) مع قوة كوريوليس الخاصة به إطارًا أكثر طبيعيةً لتفسير حركات الهواء مقارنةً مع الإطار القصوري غير الدوراني الخالي من قوة كوريوليس. في هندسة المدفعية بعيدة المدى، تعتمد تصحيحات دوران الأرض البصرية على قوة كوريوليس.[16]
الصيغة
تعطى صيغة المتجه لقيمة واتجاه تسارع الكوريوليس بالعلاقة
حيث v سرعة الجسيم في نظام دوار، وΩ متجه السرعة الزاوية والتي لها قيمة معدل الدوران ω وتكون متجهة نحو محور الدوران للإطار المرجعي الدوار، والرمز × يبين عامل ضرب المتجه.
يمكن ضرب المعادلة بكتلة الجسم للحصول على قوة الكوريوليس:
- .
يمكن تقييم الضرب المتجهي بمحدد المصفوفة:
حيث أن المتجهات i, j, k هي متجهات الوحدة باتجاه x, y وz.
تطبيقات
الأعاصير

يمكن ملاحظة تأثير الكوريوليس في الحياة العملية مثلا لتفسير دوران الأعاصير شمال وجنوب الكرة الأرضية. نظرا لاختلاف درجات الحرارة عند كل من القطبين وعلى خط الاستواء، فإن فرقاً في الضغط الجوي ينشأ دافعاً في الهواء من القطبين نحو خط الاستواء. أثناء سير الرياح فإنها تتعرض لظاهرة الكوريوليس ولما كانت الكرة الأرضية تدور باتجاه الشرق فإن تخلف حركة الرياح تظهر باتجاه خط الاستواء ونحو الغرب. يظهر هذا في شكل أعاصير، لها اتجاه عقارب الساعة شمال الكرة الأرضية، وعكس عقارب الساعة جنوب الكرة الأرضية.
رقاص فوكو
يمثل رقاص فوكو أول تطبيق عملي استعمل لإثبات دوران الأرض حول محورها بحيث يبدو هذا جلياً للمشاهدين. يبلغ طول رقاص فوكو 67 متراً وبه ثقل كتلته 28 كغم. يستطيع هذا الرقاص أيضا تمييز دوائر العرض.
فكرة خاطئة
هناك من يسمع عن تأثير الكوريوليس، واختلاف دوران الأعاصير شمال وجنوب الكرة الأرضية، فيظن أن الأمر نفسه ينطبق على المسطحات المائية الصغيرة، مثل مغاسل المياه والحمامات. للأسف فإن هذه المعلومة الخاطئة قد انتشرت حتى في بعض شبكات التلفزة والإذاعة والأخبار. في الحقيقة لايمكن الجزم بتطبيق هذه الظاهرة على التحركات ذات المسافات القصيرة جدا نسبة إلى قطر الكرة الأرضية بل إن مايحدث في المغطس أو المغسلة من دوران يختلف بحسب طبيعة السطح المائي واتجاه الحركة الأولي. على سبيل المثال يمكن لصنبور المياه جعل الاتجاه مع أو عكس عقارب الساعة بمجرد ميلان صغير أثناء السقوط على السطح.
انظر أيضا
مراجع
- ^ "معلومات عن تأثير كوريوليس على موقع snl.no". snl.no. مؤرشف من الأصل في 2016-10-22.
- ^ "معلومات عن تأثير كوريوليس على موقع jstor.org". jstor.org. مؤرشف من الأصل في 2020-04-12.
- ^ "معلومات عن تأثير كوريوليس على موقع psh.techlib.cz". psh.techlib.cz. مؤرشف من الأصل في 2019-12-14.
- ^ Graney، Christopher M. (2011). "Coriolis effect, two centuries before Coriolis". Physics Today. ج. 64 ع. 8: 8. Bibcode:2011PhT....64h...8G. DOI:10.1063/PT.3.1195.
- ^ Persson, A. "The Coriolis Effect: Four centuries of conflict between common sense and mathematics, Part I: A history to 1885." History of Meteorology 2 (2005): 1–24.
- ^ Truesdell, Clifford. Essays in the History of Mechanics. Springer Science & Business Media, 2012., p. 225
- ^ Cartwright، David Edgar (2000). Tides: A Scientific History. Cambridge University Press. ص. 74. ISBN:9780521797467. مؤرشف من الأصل في 2020-05-09.
- ^ G-G Coriolis (1835). "Sur les équations du mouvement relatif des systèmes de corps". J. De l'Ecole Royale Polytechnique. ج. 15: 144–154.
- ^ Dugas, René and J. R. Maddox (1988). A History of Mechanics. Courier Dover Publications: p. 374. (ردمك 0-486-65632-2) نسخة محفوظة 20 ديسمبر 2019 على موقع واي باك مشين.
- ^ Bartholomew Price (1862). A Treatise on Infinitesimal Calculus : Vol. IV. The dynamics of material systems. Oxford : University Press. ص. 418–420. مؤرشف من الأصل في 2020-05-09.
- ^ Edwin b. Wilson (1920). James McKeen Cattell (المحرر). "Space, Time, and Gravitation". The Scientific Monthly. ج. 10: 226. مؤرشف من الأصل في 2020-05-09.
- ^ William Ferrel (نوفمبر 1856). "An Essay on the Winds and the Currents of the Ocean" (PDF). Nashville Journal of Medicine and Surgery. ج. xi ع. 4: 7–19. مؤرشف من الأصل (PDF) في 11 أكتوبر 2013. Retrieved on 1 January 2009.
- ^ Anders O. Persson. "The Coriolis Effect:Four centuries of conflict between common sense and mathematics, Part I: A history to 1885" (PDF). Swedish Meteorological and Hydrological Institute. مؤرشف من الأصل (PDF) في 2014-04-11. اطلع عليه بتاريخ 2006-02-26.
{{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب|دورية محكمة=(مساعدة) - ^ Gerkema، Theo؛ Gostiaux، Louis (2012). "A brief history of the Coriolis force". Europhysics News. ج. 43 ع. 2: 16. Bibcode:2012ENews..43b..14G. DOI:10.1051/epn/2012202.
- ^ Schneider، Stephen H.؛ Root، Terry L.؛ Mastrandrea، Michael، المحررون (2011). Encyclopedia of Climate and Weather. Oxford University Press. ج. 3. ص. 310.
- ^ Roger Graham Barry؛ Richard J. Chorley (2003). Atmosphere, Weather and Climate. Routledge. ص. 113. ISBN:978-0-415-27171-4. مؤرشف من الأصل في 2020-05-09.
| تأثير كوريوليس في المشاريع الشقيقة: | |