الفراغات المعيرة وفراغات بناخ

نجد في الرياضيات فكرة وهي إن طول القطعة المستقيمة في المستوى ${\mathbf{R}}^{\mathbf{2}}$ ونقطتي النهاية لهذه القطعة مستقيمة هما (0,0) وأي زوج مرتب $x$=($\beta$ , $\alpha$) ففكرة إيجاد طول المتجه $x$ فكرة بديهية ويمكن تعميمها لأى فراغ اتجاهى حقيقى ${\mathbf{R}}^{\mathbf{n}}$ وهذه هي الخصائص لطول المتجه $x$ ويرمز له بالرمز $\left|x\right|$ :

هذا وصف لطول المتجه x في المستوى

1- أي متجه طوله موجب

2- المتجه الصفرى طوله صفر وأيضا إذا كان طول المتجه صفر فيكون هو المتجه الصفرى

3- ضرب متجه في قيمة قياسية يغير طوله بنفس مقدار القيمة المطلقة دون تغير اتجاه المتجه

حيث أن هذه القيمة القياسية إذا كانت تقع في الفترة $(-1,1)$ فإن طول المتجه $x$ ينكمش وإذا كانت تاخذ أي قيمة تقع في الفترة $\mathbf{R}-(-1,1)$ فإن طول المتجه $x$ يتمدد

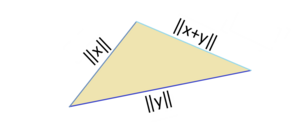
4- متباينة المثلث متحققه حيث أن طول أي ضلع في المثلث لا يزيد عن مجموع طولى الضلعين الآخرين

هذا توضيح لمتباينة المثلث في المستوى

و بتجريد هذه الخصائص لأى فراغ اتجاهى نحصل على مفهوم المعيار ألا وهو كمية مجرده ، فمن الممكن أن تصف طول أو حجم أو مدى أي فراغ وبالتالى يكون المعيار مفهوم المسافة في الفراغ الخطى وهذا يتيح لنا معرفة تقارب متسلسلة لانهائية في هذا الفراغ ، وهذا نهتم به في حل عدد لانهائي من المعادلات الخطية ومن هنا كانت بداية التحليل الدالى عندما تعثر الجبر الخطى في حل تلك المعادلات اللانهائية وعلى سبيل المثال عند تحويل معادلة تكاملية إلى نظام من المعادلات الخطية اللانهائية فهنا يظهر لنا متسلسلات لانهائية وبالتالى نريد معرفه تقاربها ، حيث نشأت نظرية بواسطة إسهامات فوليترا (1940-1860)Volterra وفريدهولم (1927-1866 )Fredholm وهيلبرت (1943-1862)Hilbert في المعادلات التكاملية.

نبذة تاريخية

أول من تكلم على مفهوم المعيار هو عالم الرياضيات النمساوى هيلى ( E.Helly( 1884 - 1943 ولكنه لم يستخدم اسم المعيار ولا رمز المعيار $|.|$ ، كان يعرفها كأى دالة ، وتحقق شروط المعيار ، وقد كتب مقالة في عام 1912 تكلم فيها عن حالة خاصة من نظرية هان - بناخ حيث أنه قام بتفسير نتائج لم يفسرها ريس (F. Riesz ( 1880 – 1956 من قبل وأيضا قام هيلى بعمل اثبات مختلف عن ريس لمد الداليات الخطية ولم يقم بنشر أي مقالات لمدة 9 سنوات بسبب الحرب العالمية الأولى وكان حينئذ سجين الحرب في روسيا ، وقام بعمل مقالة في عام 1921 ، وهذه المقالة تعتبر علامة بارزة في تاريخ التحليل الدالى حيث أنه بدل النظر إلى فراغ معين مثل $C[a,b]$ وL^p و${\ell }^p$ فهو أول من تعامل بصفة عامة مع «الفراغات المعيارية للمتتابعات» باستخدام الأساليب التي لا تعتمد على صفات خاصة للفراغ أي أن بواسطة هيلى في عام 1921 قام بتعميم نظرية نظام من المعادلات الخطية من الفراغ ${\ell }^p$ إلى أي فراغ جزئي معيارى من ${\mathbf{c}}^{\mathbf{N}}$ وهو فراغ كل المتتابعات من الأعداد المركبة وقد قام هيلى بتعريف مفهوم التحدب على الفراغات المعيرة وكان منيكوفسكى ( 1909-1864)Minkowski في عام 1911 ذكر مفهوم التحدب في هندسة الأعداد.

في عام 1920 عرف ما يسمى فراغ بناخ وطرحت فكرة فراغ بناخ من قبل بعض العلماء ، وعلى سبيل المثال وينر (1964 -1894)Norbert Wiener قدم المفاهيم ، ولكنه لم يؤسس النظريات والذي صاغ اسم فراغ بناخ هو فريشيه وأهمية اسهام بناخ انه طور منهجية نظرية التحليل الدالى حيث أنه كان يوجد نتائج معزولة تطورت فيما بعد لتتلاءم مع النظرية الجديدة .واتخذت خطوة أخرى في التجريد من قبل بناخ في عام 1932 عندما انتقل من فراغ الضرب القياسى إلى فراغ المعيار ، وأخذ بناخ الداليات الخطية لفريشيه ، وأوضح أن لديهم وضعا طبيعيا في فراغات المعيار ، وأثبت بناخ عددا من النتائج الأساسية في الفراغات الخطية المعيـرة ، وعديد من النظريات الهامة تسمى باسمه من بعده . و هناك نظرية هان - بناخ بشأن تمديد الداليات الخطية المتصلة ونظرية بناخ - شتاينهاوس ونظرية بناخ للنقطة الثابتة.

التعريف

المعيار(النظيم) : المعيار على فراغ اتجاهى x هي دالة,$\mathbf{R}$$\to$ $X$: $|.|$ , التي تحقق هذه الخواص :

لكل $x$ , $y$ تنتمى للفراغ الاتجاهى $X$ ولكل $\alpha$ تنتمى للحقل$\mathbf{k}$ ($\mathbf{R}$ or $\mathbf{C}$)

1- $\left|x\right|>0$ إذا كان $x\ne 0$ (المعيار موجب )

2- $\left|x\right|=0$ إذا كان وفقط إذا كان $x=0$ (المعيار محدد)

3- $\left|\alpha x\right|=\left|\alpha \right|\left|x\right|$ (المعيار متجانس إيجابيا)

4- $|x+y|\le \left|x\right|+\left|y\right|$ (المعيار يحقق متباينة المثلث)

-الفراغ المعيارى هو الزوج ($|.|$,$X$) عندما يكون $X$ فراغ اتجاهى معرف عليه معيار

-الفراغ الشبه معيارى هو الزوج ($p$,$X$) عندما تكون $X$ فراغ اتجاهى و$p$ شبة معيار على X

شبه معيارى هو الذي يحقق الشروط ( 1 )و( 3 )و( 4 )

-أي فراغ معيارى ($|.|$,$X$) يكون فراغ المسافة وهذا يتحقق من خواص المعيار مباشرة ودالة المسافة $d$ وهي المسافة بين متجهين$x$ , $y$ تنتمى $X$ ومعرف بهذه الصورة :

$d(x,y)=|x-y|$

ولكن ليس كل فراغ المسافة فراغ معيارى ويوجد نظرية مساعدة تبين ان دالة المسافة $d$ على الفراغ الاتجاهى $X$ الناتج بواسطة المعيار ولابد ان تحقق هذين الشرطين وهما :

أ) $d(x,y)=d(x+a,y+a)$ (إزاحة ثابته)

ب) $d(\alpha x,\alpha y)=\left|\alpha \right|d(x,y)$ ( التجانس )

وهذا يعنى أنه إذا لم يتحقق واحد من الشرطين يترتب على هذا أنه لا يمكننا تعريف معيار على هذا الفراغ الاتجاهى $X$

و باستخدام دالة المسافة يمكننا تعريف اتصال دالة المعيار

-دالة المعيار $|.|$ دالة متصلة وهذا ينتج من المتباينة التالية:

$|x-y|\ge \left|\right|x|-|y\left|\right|$ لكل $x$ , $y$ تنتمى للفراغ الاتجاهى $X$

- ليكن الزوج ($|.|$,$X$) فراغ معيارى

التقارب - المتتابعة ${(}_{x_n}$ في $X$ تكون تقاربية ل $x$ في $X$ إذا كان لكل $ϵ>0$ يوجد $\mathbf{N}$ $\in$ $n_0$ لكل $\mathbf{N}$ $\in$$n$ بحيث لكل $n_0$ < $n$ $\Leftarrow$ $|x_n-x|$ $ϵ>$

الكوشية - المتتابعة ${(}_{x_n}$ في $X$ تكون كوشية إذا كان لكل $ϵ>0$ يوجد$\mathbf{N}$ $\in$ $n_0$ لكل $\mathbf{N}$ $\in$$n$,$m$ بحيث لكل $n_0$ < $n$ ,$m$ $\Leftarrow$ $|x_n-x_m|$ $ϵ>$

-فراغ بناخ هو فراغ معيارى كامل وهذا يعنى ان كل متتابعة كوشية لها نهاية في هذا الفراغ.

أمثلة

• الفراغ الإقليدي ${\mathbf{R}}^{\mathbf{n}}$ هو فراغ كامل ومعرف عليه معيار كالتالي :

$\left|\mathit{x}\right|=\sqrt{x_1^2+\cdots +x_n^2}$ عندما $\mathit{x}$ = (x₁, x₂, ..., x_n)

وبالتالي هذا الفراغ فراغ بناخى

• الفراغ المركب ${\mathbf{C}}^{\mathbf{n}}$ هو فراغ كامل ومعرف عليه معيار كالتالي :

$\left|\mathit{z}\right|=\sqrt{|z_1{|}^2+\cdots +|z_n{|}^2}=\sqrt{z_1{\overline{z}}_1+\cdots +z_n{\overline{z}}_n}$

وبالتالي هذا الفراغ فراغ بناخى

• معيار تشيبيشيف ويسمى أيضًا بمعيار $L^{\mathrm{\infty }}$وهو معيار L^p عندما $p\to \mathrm{\infty }$ وهو فراغ كامل ومعرف علية معيار كالتالى :

$\underset{p\to \mathrm{\infty }}{lim}|x{|}_p=\underset{p\to \mathrm{\infty }}{lim}{(|x_1{|}^p+|x_2{|}^p+\cdots +|x_n{|}^p)}^{\frac{1}{p}}=|x{|}_{\mathrm{\infty }}=max\{|x_1|,|x_2|,\dots ,|x_n|\}$

و بالتالى هذا الفراغ فراغ بناخى

• فراغ ℓ^p هو فراغ المتتابعات اللانهائية من الأعداد حيث أن هذه المتسلسلة $\sum _{n=1}^{\mathrm{\infty }}|x_n{|}^p$ تكون تقاربية وهو فراغ كامل ومعرف علية معيار كالتالى :

p $⩾$ 1,$\left|x\right|={(\sum _{n=1}^{\mathrm{\infty }}|x_n{|}^p)}^{1/p}$

و بالتالى هذا الفراغ فراغ بناخى

• $C_p[a,b]$ فهو فراغ الدوال المتصلة على الفترة $[a,b]$ فهو فراغ غير كامل ولكن معرف عليه معيار :

p $⩾$ 1 , $\left|x\right|={(\underset{a}{\overset{b}{\int }}|x(t){|}^{p}dt)}^{1/p}$

و بالتالي فهو ليس فراغ بناخى واكتماله هو (L^p(a,b وهو فراغ ليبيج للدوال القابلة للتكامل وهو فراغ بناخى

• $p$ شبه معيارى معرف كالتالى : $p(x)=0$ لكل $x$ $\ni$ $X$

ويوجد أيضًا أمثلة توضح وجود فراغات المسافة ولكن ليست فراغات معيارية:

• $s$ فراغ كل المتتابعات وهذا الفراغ معرف عليه مسافة كالتالي:

$d(x,y)=\sum _{n=1}^{\mathrm{\infty }}\frac{1}{2^n}\frac{|x_n-y_n|}{1+|x_n-y_n|}$

ولكن هذه المسافة لا يمكننا تعريف معيار عليه وهذا يتضح باستخدام النظرية المساعدة حيث أن الشرط (ب) لم يتحقق وبالتالي هذا الفراغ لم يكن فراغ بناخى

• المسافة المنفصلة ٍ$\rho$ معرف على $X$ كالتالى:

$\rho (x,y)=\{\begin{array}{cc}1& x\ne y\\ 0& x=y\end{array}$ لكل $y$ ,$x$ $\ni$ $X$

وهذه المسافة المنفصلة لا يمكننا تعريف معيار عليه هذا يتضح باستخدام النظرية المساعدة حيث أن الشرط (ب) لم يتحقق وبالتالي، إذًا الفراغ لم يكن فراغ بناخى

التطبيقات

• يستخدم الفراغ المعيارى وفراغ بناخ في الاقتصاد وفي التطبيقات المالية [1][2]
• ويطبق أيضا في علم الوراثة [3]
• ويطبق في الفيزياء [4] [5]
• ويطبق في الهندسة الكيميائية [6] ويطبق أيضا في كيمياء الكم [7] صفحة 139
• ويطبق في الإحصاء [8]
• ويستخدم في نظرية التحكم الأمثل [9][10]

انظر أيضا

• فراغات حاصل الضرب القياسى وفراغات هيلبرت
• التحليل الدالى
• نظريات هامة في التحليل الدالى
• ستيفان بناخ

المراجع

• J. Dieudonné, History of Functional Analysis, North-Holland, 1981 [11]
• E. Kreyszig, Introductory Functional Analysis with Applications, Wiley , 1978 [12]
• Y. Eidelman, V. Milman and A. Tsolomitis, Functional Analysis: An Introduction, AMS , 2004 [13]
• K. Saxe, Beginning Functional Analysis, Springer , 2002 [14]
• Mario J. Mirand , Paul L. Fackler , Applied Computational Economics And Finance , the MIT press , 2002
• Pier Carlo Nicola , Mainstream Mathematical Economics in the 20th Century, Springer , 2000
• Yvonne Choquet-Bruhat, Cécile DeWitt-Morette, Margaret Dillard Bleick, Analysis, manifolds, and physics, North Holland , 1977
• Sadri Hassani, Mathematical Physics: A Modern Introduction to Its Foundations, springer , 1999
• Peter Wolenski , Martin A. Hjortso, Linear Mathematical Models In Chemical Engineering ,world scientific , 2010
• 2011 , .Advances in Quantum Chemistry,Elsevier Inc, John R. Sabin ,Erkki J. Brändas
• 2010 , Alexander J. Zaslavski ,Optimization on Metric and Normed spaces, springer
• 1980 , .James R. Leigh , Functional Analysis and Linear Control Theory , ACADEMIC PRESS INC