|
تضامنًا مع حق الشعب الفلسطيني |
الجوار (نظرية الرسومات)
- لتوضيحات أخرى لمفهوم الجوارات في الرياضيات، يرجى الرجوع لـ جوار (رياضيات) .
- لمفهوم الجوارات الغير متعلق بمجال الرياضيات يرجى زيارة Neighbourhood (disambiguation).
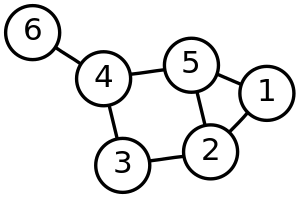
في نظرية الرسومات، يقال عن رأس انه رأس مجاور (adjacent vertex) للرأس في الرسم إذا كان مرتبط بالرأس بواسطة ضلع. الجوار (neighbourhood) للرأس في الرسم هي رسم جزئي مولد بواسطة كل الرؤوس المجاورة لـ . بمعنى آخر، جوار الرأس هو الرسم المكون من الرؤوس المجاورة لهذا الرأس وجميع الأضلاع التي تربط الرؤوس المجاورة بـ . على سبيل المثال، بالصورة المرفقة هنا، الجوار للرأس يتكون من الرؤوس و و والضلع الذي يربط الرأسين و .
في اغلب الحالات يستخدم الرمز أو للرمز لمجموعة الجوار للرأس في الرسم . هذه المجموعه لاتشمل الرأس نفسه فبتالي يمكن تسميتها أيضا بمجموعة الجوار المفتوحة (open neighbourhood) للرأس . يوجد مجموعه جوار أخرى تسمى بالجوار المغلقه (closed neighbourhood) والتي تحتوي على الرأسويرمز لهذه المجموعه بالرمز . فيما يلي عند ذكر مصطلح جوار بدون تحديد فنعني بذلك المفتوحه.
من الممكن استخدام مفهوم الجوارات لتمثيل الرسومات في خوارزميه حاسوبيه من خلال قائمة الجوار ومصفوفة الجوار الممثله لهذه الرسومات. يستخدم مصطلح الجوارات ايضاً في معامل التجميع (clustering coefficien ) لرسم ما والذي يهتم بقياس متوسط كثافة التجاور لهذا الرسم. بالإضافة إلى ذلك من الممكن تعريف تصنيفات مهمه للرسومات بناء على خواص التجاور لها أو بالتماثل والتي تربط كل جوار بالآخر.
يٌسمى الرأس الذي ليس له رؤوس مجاوره بالرأس المنعزل (isolated vertex). درجة رأس ما تساوي عدد الرؤوس المجاورة لهذا الرأس. في حالة كان الرأس مجاور لنفسه فإنه يسمى بـ عروه (loop). في حالة وجود عروه لرأس ما فإن هذا الرأس ينتمي لمجموعة التجاور لنفسه.
خصائص محلية في الرسومات
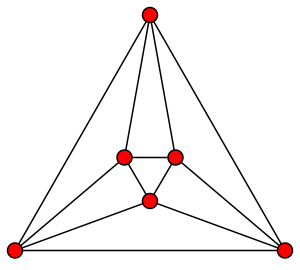
في حالة كانت كل رؤوس في الرسم
لديها تجاورات متشاكله للرسم
فإنه يقال فيه هذه الحالة أن الرسم
هو محلياً (locally) الرسم
. وإذا كانت كل الرؤوس في
لها جوارات تنتمي لنفس عائلة الرسومات
فإنه يقال أن
محليا في
.[1][2] على سبيل المثال، في الرسم ثماني الأوجه الموضح بالشكل المرفق نجد أن كل رأس له تجاور متشاكل لدوره من أربع رؤوس فبتالي فإن الرسم ثماني الاوجه (octahedron graph ) هو محليا دوره بطول
أي
.
- أي رسم مكتمل يعتبر محليا. الرسوم الوحيده التي تعتبر مكتمله محليا هي الاتحادات المنفصله لرسومات مكتمله.
- رسم توران (Turán graph ) هو محليا . بشكل عام فإن أي رسم توران يعتبرتوران محليا.
- نقول أن الرسم خالي من المثلثات (triangle-free ) إذا وفقط إذا كان مستقل محلياً.
- أي رسم به العدد اللوني يساوي (k-chromatic) فإن العدد اللوني المحلي يساوي . أي رسم بعدد تلوين محليا لديه عدد تلوين .[3]
- إذا كانت عائلة من الرسومات مغلقه بالنسبة لعملية الرسوم الجزئية المولدة، فإن كل رسم في أيضا ينتمي لـ محليا.
- أي رسم يمثل دوره محليه إذا كان مجموعه الجوار له أيضا دوره.
- الرسوم الخطية محليا هي رسومات التي بها مجموعة الجوار هي متطابقة مولدة.
جوار مجموعة
لأي مجموعة من الرؤوس ، فإن تجاور المجموعة هي عبارة عن اتحاد تجاورات رؤوسها.
المزيد
مراجع
- ^ Hell، Pavol (1978). [Graphs with given neighborhoods I "Problèmes combinatoires et théorie des graphes"]. Colloques internationaux C.N.R.S. ج. 260: 219–223.
{{استشهاد بدورية محكمة}}: الاستشهاد بدورية محكمة يطلب|دورية محكمة=(مساعدة) وتحقق من قيمة|مسار=(مساعدة) - ^ Sedláček، J. (1983). "On local properties of finite graphs". Graph Theory, Lagów. Lecture Notes in Mathematics. Springer-Verlag. ج. 1018. ص. 242–247. DOI:10.1007/BFb0071634. ISBN:978-3-540-12687-4.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة) - ^ Wigderson، Avi (1983). Improving the performance guarantee for approximate graph coloring. ج. 30. ص. 729–735. DOI:10.1145/2157.2158.
{{استشهاد بكتاب}}: يحتوي الاستشهاد على وسيط غير معروف وفارغ:|بواسطة=(مساعدة)