ارتباط جزئي

حالة يكون فيها المتغير $Z$ مفسرا قبليا جزئيا ل$X$ و$Y$ معا

الارتباط الجزئي (بالإنجليزية: Partial Correlation)‏ في الإحصاء وعلم الاحتمالات، وفي سياق اعتبار أكثر من متغيرين عشوائيين، هو قياس لدرجة الارتباط بين متغيرين اثنين بتحييد تأثيرات المتغيرات الأخرى.

عمليا، هذا التحييد يتم، في حالة ثلاثة متغيرات $X$، $Y$ و$Z$، بتحييد نسبة التباين التي تعزى ل $Z$. حساب معامل الارتباط الجزئي هنا يكون حسب الصيغة التالية:

$r_{XY,Z}=\frac{r_{XY}-r_{XZ}{r}_{YZ}}{\sqrt{1-r_{XY}^2}\sqrt{1-r_{XZ}^2}}$

بحيث تشير المعاملات $r$ إلى قيم الارتباط حسب بيرسون.

غالبا ما يشار في المراجع الإحصائية إلى المتغير $Z$ بتسمية عامل الالتباس (أو عامل الخلط).

حساب (أو تحليل) الارتباط الجزئي ممكن أيضا في الحالة التي يكون فيها $Z$ متغيرا نوعيا: في هذه الحالة تتم مقارنة معاملات الارتباط $r_{XY}$ داخل المجموعات المعرفة حسب قيم $Z$.

يمكن قياس الارتباط الجزئي باعتبار أكثر من عامل التباس، في هذه الحالة الصيغة السابقة تسمى معامل ارتباط جزئي من الرتبة الأولى. في حالة وجود $p$ متغير للتحييد، نكون في حالة معامل ارتباط جزئي من الدرجة $p$.

الأهمية الإحصائية

في الكثير من الدراسات الإحصائية، تلعب دراسات الارتباط دورا حاسما في تأطير وتوجيه الدراسة خلال المرحلة الاستكشافية. الاكتفاء بتقعيد الاستنتاجات والخلاصات عبر حساب معاملات الارتباط الكبرى، دون اعتبار مسألة الارتباط الجزئي، يمكن أن يؤدي إلى مغالطات واستنتاجات غير مبنية، بل يمكن أن يضرب منهجية الدراسة من الأساس. الارتباط الجزئي مهم أيضا في عمليات كشف التداخل الخطي وتحليله وتشكل مرحلة ضرورية خلال تحليلات الانحدار الخطي والمتسلسلات الزمنية.

أهميته في الاستدلال الإحصائي

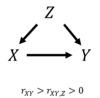
غالبا ما يكون الهدف من تحليلات الاستدلال الإحصائي الكشف عن علاقات سببية بين المتغيرات أو الظواهر المدروسة. هذه العملية غالبا ما تحفها مخاطر منهجية لعدم وجود تقابل بين مفهومي الارتباط والسببية. تحليل الارتباط الجزئي (إضافة لتقنيات أخرى مثل التداخل الخطي) تقنية تساعد على تقريب المفهومين وقد تسرع حسم أو نفي فرضيات سببية مثلما قد تفند «حقائق» إحصائية ناتجة عن تطبيق سطحي لمعاملات الارتباط الكلاسيكية. تعرض المراجع الإحصائية أمثلة عديدة لهذا النوع من المشاكل المنهجية. مثلا:

• في بلد معين يمكن أن نلاحظ، عبر السنوات، وجود ارتباط إحصائي بين عدد محلات الأكلات السريعة ونسبة الناس المتعلمين: هل يمكن تأكيد فرضية تقول بأن وفرة هذا النوع من المحلات هي التي تؤدي إلى تجويد مستوى التعلم؟
• الارتباط بين مبيعات النظارات الصيفية ومبيعات الثلج خلال فصل الصيف: من الصعب افتراض أن ارتفاع استهلاك الثلج يؤدي إلى ارتداء النظارات الصيفية، كلا الظاهرتين محفزتان بسبب الفصل أو نسبة الأيام المشمسة.

الجدول التالي يجرد جميع الحالات الممكنة للعلاقة بين السببية ومفهومي الارتباط والارتباط الجزئي:

حالات العلاقات الممكنة بين السببية والارتباط والارتباط الجزئي، باعتبار ثلاثة متغيرات $X$، $Y$ و$Z$

الحالة	قيم المعاملات	شكل العلاقة
$Z$ لا تتدخل في تفسير $X$ ل$Y$	$r_{XY}=r_{XY,Z}$
$Z$ مفسر قبلي تام ل$X$ و$Y$ معا	$r_{XY,Z}=0$
$Z$ مفسر تام ل $X$ في علاقتها ب$Y$	$r_{XY,Z}=0$
$Z$ مفسر قبلي جزئي ل$X$ و$Y$ معا	$r_{XY}>r_{XY,Z}>0$
$Z$ مفسر جزئي ل $X$ في علاقتها ب$Y$	$r_{XY}>r_{XY,Z}>0$
$Z$ مفسر مغالط تام ل $X$ و$Y$ معا	$r_{XY}=0$ و$\left|r_{XY,Z}\right|>0$
$Z$ مفسر مغالط جزئي ل $X$ و$Y$ معا	$\left|r_{XY,Z}\right|>\left|r_{XY}\right|$

ينبغي التأكيد هنا على أن وجود ارتباط جزئي لا يكافئ بالضرورة وجود علاقة سببية بين المتغيرين المدروسين: على غرار معاملات الارتباط المطلقة، حساب الارتباط هو مؤشر موجه للدراسة ويجب دعمه، قبليا، بتقعيدات نظرية للعلاقات السببية لا تكون بالضرورة إحصائية، بل مستنبطة من المعارف النظرية المتراكمة في مجال الدراسة.

الارتباط الجزئي من الرتبة الأولى

تعريف

باعتبار ثلاثة متغيرات $X$، $Y$ و$Z$، وبالإشارة إلى معامل ارتباط بيرسون ب $r$، يعرف معامل الارتباط الجزئي $r_{XY,Z}$ حسب الصيغة التالية:

$r_{XY,Z}=\frac{r_{XY}-r_{XZ}{r}_{YZ}}{\sqrt{1-r_{XY}^2}\sqrt{1-r_{XZ}^2}}$

وهو قياس لقوة العلاقة بين $X$ و$Y$ بتحييد تأثير المتغير $Z$. هذا التحييد يتم عبر حذف جداء معاملي ارتباط $X$ و$Y$ مع $Z$. مقام الصيغة هو بمثابة معيرة للمعامل حتى تكون قيمه ضمن المجال $[-1,1]$.

فرضيات

مقاربة الارتباط حسب بيرسون المستخدمة هنا تورث لمعامل الارتباط الجزئي المعرف فرضيات الاستدلال الإحصائي المستخدمة في تحليل الارتباط:

• التوزيع الشرطي ل $(X,Y/Z)$ يجب أن يكون موزعا وفق توزيع طبيعي ثنائي.
• يجب توفر علاقات خطية بين المتغيرات المدروسة.

المقدر

مقدر المعامل يتم حسابه بحساب مقدرات المعاملات التي تدخل في صيغة التعريف:

${\hat{r}}_{XY,Z}=\frac{{\hat{r}}_{XY}-{\hat{r}}_{XZ}{\hat{r}}_{YZ}}{\sqrt{1-{\hat{r}}_{XY}^2}\sqrt{1-{\hat{r}}_{XZ}^2}}$

اختبار المغزى الإحصائي

اختبار المغزى الإحصائي للمعامل يكافئ اختبار استقلال المتغيرين الشرطيين $(X/Z)$ و$(Y/Z)$.

الفرضية المنعدمة للاختبار هي $H_0:r_{XY,Z}=0$

إحصائية الاختبار هي $t=\frac{\hat{r}}{\sqrt{\frac{1-{\hat{r}}^2}{n-3}}}$ مع اعتبار $n$ حجم العينة المدروسة.

$t$ موزعة حسب توزيع ستيودنت ب $(n-3)$ درجات حرية. يتم رفض الفرضية المنعدمة إذا كانت القيمة الاحتمالية (p-value) أصغر من عتبة الخطأ (0.05 مثلا) الموضوعة.