نظام ديناميكي تسلسلي

فضاء الطور الخاص بالنظام الديناميكي التسلسلي

إن الأنظمة الديناميكية التسلسلية هي مجموعة من الأنظمة الديناميكية البيانية. وهي أنظمة ديناميكية منفصلة تقوم بتعميم السمات الخاصة بها، مثل الخلايا ذاتية السلوك التقليدية، وتعمل على خلق بنية تعمل على دراسة العمليات غير المتزامنة من خلال المخططات. يستخدم التحليل الخاص بالأنظمة الديناميكية التسلسلية تقنيات من التوافقيات والجبر التجريدي ونظرية المخططات و الأنظمة الديناميكية ونظرية الاحتمال.

التعريف

يتكون أي نظام ديناميكي تسلسلي من العناصر التالية:

• رسم بياني محدود Y مع مجموعة زوايا قائمة v[Y] = {1,2, ... , n}. بالاعتماد على القرينة يمكن توجيه الرسم البياني أو عدم توجيهه.
• يمكن أخذ وضعx_v كل زاوية قائمةi منY من مجموعة محدودة K. وتكون حالة النظام هي n-مجموعة الحقول المترابطة x = (x₁, x₂, ... , x_n)، و مجموعة الحقول المترابطة x[i] تتألف من أوضاع متصلة بزوايا قائمة neighborhood-1i فيY (في بعض الترتيبات المحددة)
• تكونوظيفة الزاوية القائمة f_i عن كل زاوية قائمة i. ترسم وظيفة الزاوية القائمة الخريطة الخاصة بهاi في الوقت t مقابل الزاوية القائمة في الوقت t + 1 بناءً على الأوضاع المتصلة 1-neighborhood من i فيY.
• الكلمة w = (w₁, w₂, ... , w_m) over v[Y].

فإنها تعد متوافقة لعرض الخرائط Y-local maps F_i المركبة من وظائف الزاوية القائمة بواسطة

$F_i(x)=(x_1,x_2,\dots ,x_{i-1},f_i(x[i]),x_{i+1},\dots ,x_n).$

تحدد الكلمة w التسلسل الذي تتألف منه الخرائط الموضعية لـY لاستنتاج خريطة النظام الديناميكي التسلسلي F: Kⁿ → Kⁿ باعتبارها

$[F_Y,w]=F_{w(m)}\circ F_{w(m-1)}\circ \cdots \circ F_{w(2)}\circ F_{w(1)}.$

إذا كان التسلسل الذي تم تحديثه أحد أنواع التبديل ويتحدث بشكل متكرر عن تبديل النظام الديناميكي التسلسلي للتأكيد على تلك النقطة. إن فضاء الطور المتصل بالنظام الديناميكي التسلسلي في خريطة ماF: Kⁿ → Kⁿ هو مخطط موجه ومحدود متصل بمجموعة الزوايا القائمةKⁿ ومخططات موجّهة (x, F(x)). يخضع تركيب فضاء الطور لخصائص المخطط Y، ووظائف الزاوية القائمة (f_i)_iوالتسلسل الذي تم تحديثه w. ويسعى الجزء الأكبر من الأبحاث في مجال الأنظمة الديناميكية التسلسلية إلى الاستدلال بخصائص فضاء الطور بناءً على مكونات النظام.

مثال

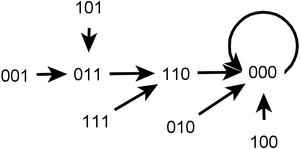
في المسألة تكون Y كالتالي: المخطط مع مجموعة الزوايا القائمة {1,2,3} والمخططات غير الموجهة {1,2} و{1,3} و{2,3} (a المثلث أو الدائرة 3-circle) مرتبطة مع مجموعات الزوايا القائمة من K = {0,1}. بالنسبة لوظائف الزوايا القائمة قم باستخدام وظيفة التماثل والوظيفة البوليانية المحددين كالتالي : K³ → K الخاصية المحددة(x,y,z) = (1+x)(1+y)(1+z) ولا تقوم باستخدام الحساب البوليني. وبالتالي، تكون الحالة الوحيدة التي ترجع فيها الوظيفة إلى القيمة 1 عندما تصل كافة الافتراضات إلى القيمة صفر. اخترw = (1,2,3) باعتباره تسلسلا تم تحديثه. يكون البدء من حالة النظام الأولية(0,0,0) في الوقت t = 0 ويحسب الشخص وضع الزاوية القائمة 1 عند الوقت t=1 وليس عند (0,0,0) = 1. وأن وضع الزاوية القائمة 2 في الوقت t=1 ولا تكون أيضا(1,0,0) = 0. مع ملاحظة أن وضع الزاوية القائمة 1 في الوقت t=1 تم استخدامها على الفور. ويأتي شخص آخر يقوم بضبط الزاوية القائمة 3 عند الوقت t=1 وعدم اعتباره أيضا عند (1,0,0) = 0. ويستكمل هذا الشخص استكمال التسلسل الذي تم تحديثه، ويختتم الشخص الأول عمله بأن تقوم الخريطة التي لا تنتمي إلى النظام التحريكي المتسلسل بنقل حالة النظام من (0,0,0) إلى (1,0,0) . تم تحويل الحالة (1,0,0) المحدد رسمها في النظام إلى (0,1,0) عن طريق التطبيق الخاص بخريطة نظام التحريك المتسلسل.

انظر أيضًا

• النظام الديناميكي البياني
• الشبكة البوليانية
• شبكة جينية تنظيمية
• الشبكة البايزية الديناميكية
• شبكة بيتري

المراجع

• Henning S. Mortveit, Christian M. Reidys (2008). An Introduction to Sequential Dynamical Systems. Springer. ISBN 0-387-30654-4.
• Predecessor and Permutation Existence Problems for Sequential Dynamical Systems
• Genetic Sequential Dynamical Systems