|
تضامنًا مع حق الشعب الفلسطيني |
مجسم دوراني
اذهب إلى التنقل
اذهب إلى البحث
المجسم الدوراني في الرياضيات هو كل جسم ينشأ عن دوران منطقة مستوية حول محور دوران مستقيم ثابت دورة كاملة، ويسمى الخط المستقيم بمحور المجسم.[1][2][3]
حساب الحجم
رموز :
- r = نصف القطر
- h = الارتفاع
- A = المساحة أو مساحة القاعدة
- V = الحجم
يتم حساب الحجم بعدة طرق، منها :
التكامل بالأقراص

للدالة
- تقوم الطريقة على تقسيم الجسم إلى أقراص غير متناهية.
محور الدوران هو المحور السيني
- إذا كان المجسم الدوراني ينتج عن دوران منطقة مستوية حول محور السينات فإنه حجمه يعطى بالمعادلة :
محور الدوران هو المحور الصادي
- إذا كان المجسم الدوراني ينتج عن دوران منطقة مستوية حول محور الصادات فإنه حجمه يعطى بالمعادلة:
بعض أنواع المجسمات الدورانية
- الأجسام الدورانية متنوعة بتنوع منحنيات الدوال، ولكن هناك أجسام مشهورة منها :
| اسم الجسم | ينشأ عن دوران | معادلة المنطقة المستوية | تمثيل الشكل | معادلة حساب الحجم |
|---|---|---|---|---|
| اسطوانة | مستطيل |  |
||
| مخروط | مثلث قائم الزاوية |  |
||
| كرة | نصف دائرة |  |
||
| مخروط ناقص | شبه منحرف | حيث H ارتفاع الجزء الناقص |
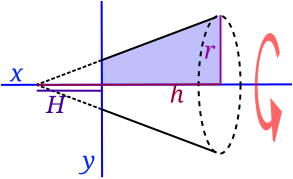 |

وبعض الأجسام قد تنتج من خلال المنطقة المحصورة بين داليتين ليست صفرية(انظر الشكل المقابل)
انظر أيضا
المصادر
- ^ "معلومات عن مجسم دوراني على موقع brilliant.org". brilliant.org. مؤرشف من الأصل في 2019-07-14.
- ^ "معلومات عن مجسم دوراني على موقع thes.bncf.firenze.sbn.it". thes.bncf.firenze.sbn.it. مؤرشف من الأصل في 2019-12-15.
- ^ "معلومات عن مجسم دوراني على موقع mathworld.wolfram.com". mathworld.wolfram.com. مؤرشف من الأصل في 2019-06-09.
- كتاب الرياضيات الصف الثالث ثانوي الصف الدراسي الثاني، ط 1431-1432 , المملكة العربية السعودية
| في كومنز صور وملفات عن: مجسم دوراني |