يرجى مراجعة هذه المقالة وإزالة وسم المقالات غير المراجعة، ووسمها بوسوم الصيانة المناسبة.

التعلم الآلي الكمي

من أرابيكا، الموسوعة الحرة
اذهب إلى التنقل اذهب إلى البحث

التعلم الآلي الكمي هو تكامل الخوارزميات الكمومية مع برامج التعلم الآلي.[1] [2] [3] يشير الاستخدام الأكثر شيوعًا للمصطلح إلى خوارزميات التعلم الآلي لتحليل البيانات الكلاسيكية التي يتم تنفيذها على جهاز كمبيوتر كمي، أي التعلم الآلي المعزز بميكانيكا الكم.[4] [5] [6] وبينما تُستخدم خوارزميات التعلم الآلي للتعامل مع كميات هائلة من البيانات، فإن التعلم الآلي الكمي يستخدم الكيوبتات والعمليات الكمومية أو يستخدم أنظمة كمومية متخصصة لتحسين السرعة الحاسوبية وتخزين البيانات الذي تقوم به خوارزميات برنامج ما.[7] ويتضمن ذلك طرقًا هجينة تدمج المعالجة الكلاسيكية والكمية، حيث يتم الاستعانة بالأجهزة الكمية لآداء أجزاء البرنامج الفرعية الصعبة حسابياً. [2] [8] [9] [10] وعلاوة على ذلك، يمكن استخدام الخوارزميات الكمومية لتحليل الحالات الكمومية بدلاً من البيانات التقليدية.[11] [12] وبعيدًا عن الحوسبة الكمومية، يرتبط مصطلح «التعلم الآلي الكمي» أيضًا بأساليب التعلم الآلي الكلاسيكية المطبقة على البيانات الناتجة عن التجارب الكمية (مثل التعلم الآلي للأنظمة الكمومية)، مثل تعلم انتقالات الطور في النظام الكمي [13] [14] أو إنشاء تجارب كمومية جديدة.[15] [16] [17] يمتد التعلم الآلي الكمومي أيضًا لينطبق على فرع من الأبحاث يستكشف أوجه التشابه المنهجية والهيكلية بين بعض الأنظمة الفيزيائية وأنظمة التعلم، مثل مجال الشبكات العصبية. على سبيل المثال، يمكن لبعض الأساليب الرياضية والرقمية من فيزياء الكم أن يتم تطبيقها على التعلم العميق الكلاسيكي والعكس صحيح.[18] [19] [20] علاوة على ذلك، يستقصي الباحثون مفاهيم أكثر تجريدا في نظرية التعلم، وهي المفاهيم التي تتعلق بالمعلومات الكمومية، والتي يشار إليها أحيانًا باسم «نظرية التعلم الكمي».[21] [22]

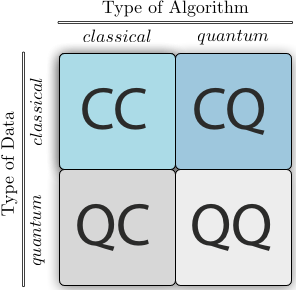
أربع طرق مختلفة للدمج بين تخصصات الحوسبة الكمومية والتعلم الآلي.[23] [24] يشير الحرف الأول إلى ما إذا كان النظام قيد الدراسة كلاسيكيًا أم كموميًا، بينما يحدد الحرف الثاني ما إذا كان يتم استخدام جهاز معالجة المعلومات الكلاسيكي أو الكمي.

التعلم الآلي باستخدام أجهزة الحاسب الكمومية

يشير التعلم الآلي المعزز بميكانيكا الكم إلى الخوارزميات الكمية التي تحل مهام في التعلم الآلي، وبالتالي تُحسن وتُوسع تقنيات التعلم الآلي الكلاسيكية في كثير من الأحيان. وتتطلب مثل هذه الخوارزميات عادةً من المرء أن يُكوّد البيانات الكلاسيكية المعطاة ليدخلها في كمبيوتر كمي ولتكون بيانات قابلة للمعالجة الكمومية. بعد ذلك، يتم تطبيق برامج معالجة المعلومات الكمية ويتم إستخلاص نتيجة الحساب الكمي عن طريق القيام بقياس النظام الكمي. على سبيل المثال، قد تكشف نتيجة قياس كيوبت معين النقاب عن النتيجة الحسابية لمسألة تصنيف ثنائي. وفي حين أن العديد من المقترحات الخاصة بخوارزميات التعلم الآلي الكمي لا تزال نظرية بحتة وتتطلب جهاز كمبيوتر كمي شامل وواسع النطاق ليتم اختبارها، فقد تم تنفيذ مقترحات أخرى على أجهزة كمية صغيرة أو ذات أغراض خاصة.

محاكاة الجبر الخطي باستخدام السعات الكمومية

يعتمد عدد من الخوارزميات الكمومية للتعلم الآلي على فكرة ترميز السعة ، أي ربط اتساعات الحالة الكمومية بمدخلات ومخرجات الحسابات.[25] [26] [27] هذا يعني أن حالة عدد n من الكيوبتات يمكن وصفها بواسطة عدد 2n من السعات المعقدة، وهذا الترميز المعلوماتي يسمح بتوفير أسي في حجم التمثيل البياناتي. تُماثل هذه العملية مسألة ربط توزيع احتمالي متقطع على متغيرات عشوائية ثنائية مع متجه كلاسيكي. والهدف من الخوارزميات القائمة على ترميز السعة هو صياغة خوارزميات كمية تنمو مواردها بشكل متعدد الحدود في عدد الكيوبتات n ، وهو ما يؤدي إلى نمو لوغاريتمي في عدد السعات وبالتالي في أبعاد المدخلات.

خوارزميات التعلم الآلي الكمومية على أساس خوارزمية بحث جروفر

وهناك نهج آخر لتحسين التعلم الآلي الكلاسيكي الذي يتضمن معالجة معلوماتية كمومية. هذا النهج يستخدم طرق تضخيم السعة بناءً على خوارزمية بحث جروفر، والتي ثبت أنها تحل مهمات البحث غير الممنهج بتسريع تربيعي مقارنة بالخوارزميات الكلاسيكية. يمكن توظيف هذه الطرق الكمية بهدف تحويل خوارزميات التعلم لمهمات بحث غير ممنهجة. وهذا هو الحال، على سبيل المثال، في خوارزمية k-medians [28] وخوارزميات أقرب k جيران. [29] وأحد التطبيقات الأخرى هو التسريع التربيعي في تدريب البيرسيبترون.

مراجع

  1. ^ Schuld، Maria؛ Petruccione، Francesco (2018). Supervised Learning with Quantum Computers. Quantum Science and Technology. DOI:10.1007/978-3-319-96424-9. ISBN:978-3-319-96423-2.
  2. ^ أ ب Schuld، Maria؛ Sinayskiy، Ilya؛ Petruccione، Francesco (2014). "An introduction to quantum machine learning". Contemporary Physics. ج. 56 ع. 2: 172–185. arXiv:1409.3097. Bibcode:2015ConPh..56..172S. DOI:10.1080/00107514.2014.964942.
  3. ^ Wittek، Peter (2014). Quantum Machine Learning: What Quantum Computing Means to Data Mining. Academic Press. ISBN:978-0-12-800953-6. مؤرشف من الأصل في 2022-03-02.
  4. ^ Wiebe، Nathan؛ Kapoor، Ashish؛ Svore، Krysta (2014). "Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning". Quantum Information & Computation. ج. 15 ع. 3: 0318–0358. arXiv:1401.2142. Bibcode:2014arXiv1401.2142W.
  5. ^ A bot will complete this citation soon. Click here to jump the queue أرخايف:[1].
  6. ^ Yoo، Seokwon؛ Bang، Jeongho؛ Lee، Changhyoup؛ Lee، Jinhyoung (2014). "A quantum speedup in machine learning: Finding a N-bit Boolean function for a classification". New Journal of Physics. ج. 16 ع. 10: 103014. arXiv:1303.6055. Bibcode:2014NJPh...16j3014Y. DOI:10.1088/1367-2630/16/10/103014.
  7. ^ Schuld, Maria; Sinayskiy, Ilya; Petruccione, Francesco (15 Oct 2014). "An introduction to quantum machine learning". Contemporary Physics (بEnglish). 56 (2): 172–185. arXiv:1409.3097. Bibcode:2015ConPh..56..172S. DOI:10.1080/00107514.2014.964942. ISSN:0010-7514.
  8. ^ Benedetti، Marcello؛ Realpe-Gómez، John؛ Biswas، Rupak؛ Perdomo-Ortiz، Alejandro (30 نوفمبر 2017). "Quantum-Assisted Learning of Hardware-Embedded Probabilistic Graphical Models". Physical Review X. ج. 7 ع. 4: 041052. arXiv:1609.02542. Bibcode:2017PhRvX...7d1052B. DOI:10.1103/PhysRevX.7.041052. ISSN:2160-3308.
  9. ^ A bot will complete this citation soon. Click here to jump the queue أرخايف:[2].
  10. ^ Schuld، Maria؛ Bocharov، Alex؛ Svore، Krysta؛ Wiebe، Nathan (2020). "Circuit-centric quantum classifiers". Physical Review A. ج. 101 ع. 3: 032308. arXiv:1804.00633. Bibcode:2020PhRvA.101c2308S. DOI:10.1103/PhysRevA.101.032308.
  11. ^ Yu، Shang؛ Albarran-Arriagada، F.؛ Retamal، J. C.؛ Wang، Yi-Tao؛ Liu، Wei؛ Ke، Zhi-Jin؛ Meng، Yu؛ Li، Zhi-Peng؛ Tang، Jian-Shun (28 أغسطس 2018). "Reconstruction of a Photonic Qubit State with Quantum Reinforcement Learning". Advanced Quantum Technologies. ج. 2 ع. 7–8: 1800074. arXiv:1808.09241. DOI:10.1002/qute.201800074.
  12. ^ Ghosh، Sanjib؛ Opala، A.؛ Matuszewski، M.؛ Paterek، T.؛ Liew، Timothy C. H. (2019). "Quantum reservoir processing". NPJ Quantum Information. ج. 5 ع. 35: 35. arXiv:1811.10335. Bibcode:2019npjQI...5...35G. DOI:10.1038/s41534-019-0149-8.
  13. ^ A bot will complete this citation soon. Click here to jump the queue أرخايف:[3].
  14. ^ Huembeli، Patrick؛ Dauphin، Alexandre؛ Wittek، Peter (2018). "Identifying Quantum Phase Transitions with Adversarial Neural Networks". Physical Review B. ج. 97 ع. 13: 134109. arXiv:1710.08382. Bibcode:2018PhRvB..97m4109H. DOI:10.1103/PhysRevB.97.134109. ISSN:2469-9950.
  15. ^ Krenn، Mario (1 يناير 2016). "Automated Search for new Quantum Experiments". Physical Review Letters. ج. 116 ع. 9: 090405. arXiv:1509.02749. Bibcode:2016PhRvL.116i0405K. DOI:10.1103/PhysRevLett.116.090405. PMID:26991161.
  16. ^ Knott، Paul (22 مارس 2016). "A search algorithm for quantum state engineering and metrology". New Journal of Physics. ج. 18 ع. 7: 073033. arXiv:1511.05327. Bibcode:2016NJPh...18g3033K. DOI:10.1088/1367-2630/18/7/073033.
  17. ^ Dunjko، Vedran؛ Briegel، Hans J (19 يونيو 2018). "Machine learning & artificial intelligence in the quantum domain: a review of recent progress". Reports on Progress in Physics. ج. 81 ع. 7: 074001. arXiv:1709.02779. Bibcode:2018RPPh...81g4001D. DOI:10.1088/1361-6633/aab406. ISSN:0034-4885. PMID:29504942.
  18. ^ Huggins، William؛ Patel، Piyush؛ Whaley، K. Birgitta؛ Stoudenmire، E. Miles (30 مارس 2018). "Towards Quantum Machine Learning with Tensor Networks". Quantum Science and Technology. ج. 4 ع. 2: 024001. arXiv:1803.11537. DOI:10.1088/2058-9565/aaea94.
  19. ^ Carleo، Giuseppe؛ Nomura، Yusuke؛ Imada، Masatoshi (26 فبراير 2018). "Constructing exact representations of quantum many-body systems with deep neural networks". Nature Communications. ج. 9 ع. 1: 5322. arXiv:1802.09558. Bibcode:2018NatCo...9.5322C. DOI:10.1038/s41467-018-07520-3. PMID:30552316. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)
  20. ^ A bot will complete this citation soon. Click here to jump the queue أرخايف:[4].
  21. ^ A bot will complete this citation soon. Click here to jump the queue أرخايف:[5].
  22. ^ Sergioli، Giuseppe؛ Giuntini، Roberto؛ Freytes، Hector (9 مايو 2019). "A new Quantum approach to binary classification". PLOS ONE. ج. 14 ع. 5: e0216224. Bibcode:2019PLoSO..1416224S. DOI:10.1371/journal.pone.0216224. PMID:31071129. {{استشهاد بدورية محكمة}}: الوسيط غير المعروف |PMCID= تم تجاهله يقترح استخدام |pmc= (مساعدة)
  23. ^ Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (7 Jun 2006). Machine Learning in a Quantum World. pp. 431–442. DOI:10.1007/11766247_37. ISBN:978-3-540-34628-9. Archived from the original on 2021-10-15. {{استشهاد بكتاب}}: |عمل= تُجوهل (help)
  24. ^ Dunjko، Vedran؛ Taylor، Jacob M.؛ Briegel، Hans J. (20 سبتمبر 2016). "Quantum-Enhanced Machine Learning". Physical Review Letters. ج. 117 ع. 13: 130501. arXiv:1610.08251. Bibcode:2016PhRvL.117m0501D. DOI:10.1103/PhysRevLett.117.130501. PMID:27715099.
  25. ^ Rebentrost، Patrick؛ Mohseni، Masoud؛ Lloyd، Seth (2014). "Quantum Support Vector Machine for Big Data Classification". Physical Review Letters. ج. 113 ع. 13: 130503. arXiv:1307.0471. Bibcode:2014PhRvL.113m0503R. DOI:10.1103/PhysRevLett.113.130503. PMID:25302877.
  26. ^ Wiebe، Nathan؛ Braun، Daniel؛ Lloyd، Seth (2012). "Quantum Algorithm for Data Fitting". Physical Review Letters. ج. 109 ع. 5: 050505. arXiv:1204.5242. Bibcode:2012PhRvL.109e0505W. DOI:10.1103/PhysRevLett.109.050505. PMID:23006156.
  27. ^ Schuld، Maria؛ Sinayskiy، Ilya؛ Petruccione، Francesco (2016). "Prediction by linear regression on a quantum computer". Physical Review A. ج. 94 ع. 2: 022342. arXiv:1601.07823. Bibcode:2016PhRvA..94b2342S. DOI:10.1103/PhysRevA.94.022342.
  28. ^ Aïmeur, Esma; Brassard, Gilles; Gambs, Sébastien (1 Feb 2013). "Quantum speed-up for unsupervised learning". Machine Learning (بEnglish). 90 (2): 261–287. DOI:10.1007/s10994-012-5316-5. ISSN:0885-6125.
  29. ^ Wiebe، Nathan؛ Kapoor، Ashish؛ Svore، Krysta (2014). "Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning". Quantum Information & Computation. ج. 15 ع. 3: 0318–0358. arXiv:1401.2142. Bibcode:2014arXiv1401.2142W.Wiebe, Nathan; Kapoor, Ashish; Svore, Krysta (2014). "Quantum Algorithms for Nearest-Neighbor Methods for Supervised and Unsupervised Learning". Quantum Information & Computation. 15 (3): 0318–0358. arXiv:1401.2142. Bibcode:2014arXiv1401.2142W.
مجلوبة من «https://3rabica.org/index.php?title=التعلم_الآلي_الكمي&oldid=3422058»