التجزئة الهندسية

في علوم الحاسوب، تعد التجزئة الهندسية طريقة فعالة لإيجاد كائنات ثنائية الأبعاد ممثلة بنقاط منفصلة خضعت لعملية تحويل تآلفي، على الرغم من وجود امتدادات لتمثيلات وتحولات الكائنات الأخرى. في خطوة خارج الخط، يتم تشفير الكائنات عن طريق معالجة كل زوج من النقاط كاساس هندسي. يمكن تمثيل النقاط المتبقية بطريقة ثابتة فيما يتعلق بهذا الأساس باستخدام عامل متغير في التجزئة. لكل نقطة، يتم تخزين إحداثياتها المحولة الكمية في جدول التجزئة كمفتاح، ومؤشرات نقاط الأساس كقيمة. ثم يتم تحديد زوج جديد من النقاط الأساسية، وتتكرر العملية من جديد. في خطوة التعرف عبر الإنترنت، يتم اعتبار أزواج نقاط البيانات المختارة عشوائيًا كقواعد مرشحة. لكل أساس مرشح، يتم ترميز نقاط البيانات المتبقية وفقًا للأساس ويتم العثور على المراسلات المحتملة من الكائن في الجدول الذي تم إنشاؤه مسبقًا. يتم قبول أساس المرشح إذا كان عدد كبير بما فيه الكفاية من نقاط البيانات مؤشرًا على أساس كائن ثابت.

تم اقتراح التجزئة الهندسية في الأصل في الرؤية الحاسوبية للتعرف على الأشياء ثنائية وثلاثية الأبعاد،^[1] ولكن تم تطبيقها لاحقًا على مشاكل مختلفة مثل التراصف البنيوي للبروتينات.^[2]^[3]

التجزئة الهندسية في الرؤية الحاسوبية

التجزئة الهندسية هي طريقة مستخدمة للتعرف على الأشياء. لنفترض أننا نريد التحقق مما إذا كان يمكن رؤية صورة نموذج في صورة إدخال. يمكن تحقيق ذلك باستخدام التجزئة الهندسية. يمكن استخدام الطريقة للتعرف على أحد الكائنات المتعددة في القاعدة، وفي هذه الحالة يجب أن يخزن جدول التجزئة ليس فقط معلومات الوضع ولكن أيضًا فهرس نموذج الكائن في القاعدة.

مثال

للتبسيط، لن يستخدم هذا المثال الكثير من ميزات النقاط ويفترض أن واصفاتها يتم تقديمها من خلال إحداثياتها فقط (في الممارسة العملية، يمكن استخدام الواصفات المحلية مثل SIFT للفهرسة).

مرحلة التدريب

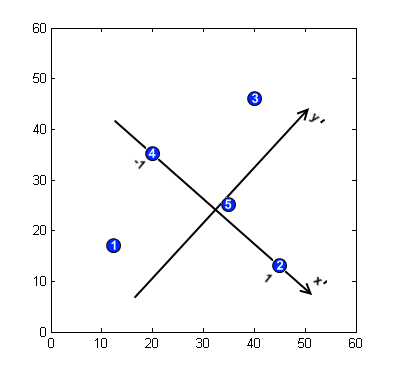
نقاط الكائن في نظام إحداثيات الصورة، ومحاور نظام الإحداثيات للأساس (P2، P4))

أوجد النقاط المميزة للنموذج. افترض أنه تم العثور على 5 نقاط مميزة في صورة النموذج بالإحداثيات $(12, 17);$ $(45, 13);$ $(40, 46);$ $(20, 35);$ $(35, 25)$ , انظر للصورة.
قدم أساسًا لوصف مواقع النقاط المميزة. بالنسبة للفضاء ثنائي الأبعاد وتحويل التشابه، يتم تحديد الأساس بزوج من النقاط. يتم وضع نقطة الأصل في منتصف المقطع الذي يربط بين النقطتين (P2، P4 في مثالنا)، يتم توجيه محور $x^{'}$ نحو إحداها، $y^{'}$ متعامد ويمر من خلال الأصل. يتم تحديد المقياس بحيث تكون القيمة المطلقة ل' $x^{'}$ ' لكلا نقطتي الأساس هي 1.

وصف مواقع الميزات فيما يتعلق بهذا الأساس، أي حساب الإسقاطات لمحاور الإحداثيات الجديدة. يجب تحديد الإحداثيات لجعل التعرف قويًا على الضوضاء، فنحن نأخذ حجم الحاوية 0.25. وبذلك نحصل على الإحداثيات $(- 0.75, - 1.25);$ $(1.00, 0.00);$ $(- 0.50, 1.25);$ $(- 1.00, 0.00);$ $(0.00, 0.25)$

قم بتخزين الأساس في جدول تجزئة مفهرس بواسطة الميزات (فقط الإحداثيات المحولة في هذه الحالة). إذا كان هناك المزيد من العناصر المراد مطابقتها، فيجب علينا أيضًا تخزين رقم الكائن جنبًا إلى جنب مع زوج الأساس.
كرر العملية مع زوج أساسي مختلف (الخطوة 2). هناك حاجة للتعامل مع انسداد. من الناحية المثالية، يجب تعداد جميع الأزواج غير القولونية. نوفر جدول التجزئة بعد تكرارين، يتم تحديد الزوج (P1، P3) للنوع الثاني.

جدول التجزئة:

Vector ( $x^{'}$ , $y^{'}$ )	basis
$(- 0.75, - 1.25);$	(P2,P4)
$(1.00, 0.00);$	(P2,P4)
$(- 0.50, 1.25);$	(P2,P4)
$(- 1.00, 0.00);$	(P2,P4)
$(0.00, 0.25)$	(P2,P4)
$(1.00, 0.00);$	(P1,P3)
$(0.00, 1.25);$	(P1,P3)
$(- 1.00, 0.00);$	(P1,P3)
$(0.00, - 0.25);$	(P1,P3)
$(0.00, 0.50)$	(P1,P3)

لا يمكن أن تحتوي معظم جداول التجزئة على مفاتيح متطابقة يتم تعيينها لقيم مختلفة. لذلك في الحياة الواقعية، لن يقوم المرء بتشفير المفاتيح الأساسية (1.0، 0.0) و (-1.0، 0.0) في جدول التجزئة.

مرحلة الاعتراف

ابحث عن نقاط مميزة مثيرة للاهتمام في صورة الإدخال.
اختر أساسًا تعسفيًا. إذا لم يكن هناك أساس تعسفي مناسب، فمن المحتمل أن صورة الإدخال لا تحتوي على الكائن الهدف.
صف إحداثيات النقاط المميزة في الأساس الجديد. حدد الإحداثيات التي تم الحصول عليها كما تم من قبل.
قارن جميع ميزات النقطة المحولة في صورة الإدخال بجدول التجزئة. إذا كانت ميزات النقطة متطابقة أو متشابهة، فقم بزيادة العدد للأساس المقابل (ونوع الكائن، إن وجد).
لكل أساس يتجاوز العد حدًا معينًا، تحقق من الفرضية التي تتوافق مع أساس الصورة المختار في الخطوة 2. انقل نظام إحداثيات الصورة إلى النموذج الأول (للكائن المفترض) وحاول مطابقته. إذا نجحت، تم العثور على الكائن. بخلاف ذلك، ارجع إلى الخطوة 2.

البحث عن نمط معكوس

يبدو أن هذه الطريقة قادرة فقط على التعامل مع القياس والترجمة والتناوب. ومع ذلك، قد تحتوي صورة الإدخال على الكائن في تحويل المرآة. لذلك، يجب أن يكون التجزئة الهندسي قادرًا على العثور على الكائن أيضًا. هناك طريقتان لاكتشاف الالنقاط المعكوسة.

للرسم البياني المتجه، اجعل الجانب الأيسر موجبًا، والجانب الأيمن سالبًا. ضرب موضع x في -1 سيعطي نفس النتيجة.
استخدم 3 نقاط للأساس. هذا يسمح باكتشاف الصور المتطابقة (أو الأشياء). في الواقع، يعد استخدام 3 نقاط للأساس طريقة أخرى للتجزئة الهندسية.

التجزئة الهندسية بأبعاد أعلى

على غرار المثال أعلاه، ينطبق التجزئة على البيانات ذات الأبعاد الأعلى. بالنسبة لنقاط البيانات ثلاثية الأبعاد، هناك حاجة أيضًا إلى ثلاث نقاط للأساس. تحدد النقطتان الأوليان المحور x، والنقطة الثالثة تحدد المحور y (مع النقطة الأولى). المحور z عمودي على المحور الذي تم إنشاؤه باستخدام قاعدة اليد اليمنى. لاحظ أن ترتيب النقاط يؤثر على الأساس الناتج.

انظر أيضا

التجزئة الحسية

المصادر

^ A.S. Mian, M. Bennamoun, and R. Owens, Three-dimensional model-based object recognition and segmentation in cluttered scenes., IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, Oct. 2006, pp. 1584-601. نسخة محفوظة 2017-10-12 على موقع واي باك مشين.
^ Moll، Mark؛ Bryant، Drew H.؛ Kavraki، Lydia E. (11 نوفمبر 2010). "The LabelHash algorithm for substructure matching". BMC Bioinformatics. ج. 11: 555. DOI:10.1186/1471-2105-11-555. ISSN:1471-2105. PMC:2996407. PMID:21070651.
^ Nussinov، R.؛ Wolfson، H. J. (1 ديسمبر 1991). "Efficient detection of three-dimensional structural motifs in biological macromolecules by computer vision techniques". Proceedings of the National Academy of Sciences of the United States of America. ج. 88 ع. 23: 10495–10499. DOI:10.1073/pnas.88.23.10495. ISSN:0027-8424. PMC:52955. PMID:1961713.

Wolfson, H.J. & Rigoutsos, I (1997). Geometric Hashing: An Overview. IEEE Computational Science and Engineering, 4(4), 10-21.

بوابة رياضيات

[Mian2006-1] A.S. Mian, M. Bennamoun, and R. Owens, Three-dimensional model-based object recognition and segmentation in cluttered scenes., IEEE Transactions on Pattern Analysis and Machine Intelligence, vol. 28, Oct. 2006, pp. 1584-601. نسخة محفوظة 2017-10-12 على موقع واي باك مشين.

[2] Moll، Mark؛ Bryant، Drew H.؛ Kavraki، Lydia E. (11 نوفمبر 2010). "The LabelHash algorithm for substructure matching". BMC Bioinformatics. ج. 11: 555. DOI:10.1186/1471-2105-11-555. ISSN:1471-2105. PMC:2996407. PMID:21070651.

[3] Nussinov، R.؛ Wolfson، H. J. (1 ديسمبر 1991). "Efficient detection of three-dimensional structural motifs in biological macromolecules by computer vision techniques". Proceedings of the National Academy of Sciences of the United States of America. ج. 88 ع. 23: 10495–10499. DOI:10.1073/pnas.88.23.10495. ISSN:0027-8424. PMC:52955. PMID:1961713.

[1]

[2]

[3]