|
تضامنًا مع حق الشعب الفلسطيني |
ثابت الالتواء
ثابت الألتواء هي خاصية هندسية لمقطع الذي يتكون من علاقة بين زاوية الألتواء وعزم محوري.
تاريخ
عام 1820، مهندس فرنسي إستنتج ثابت الألتواء من عزم القصور الذاتي لكمرة.[1]
إستنتاج جزئي
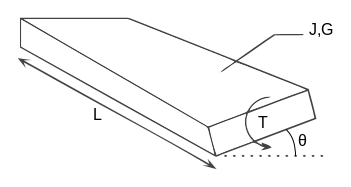
لكمرة عرض قطاعها منتظم:
حيث :
مثال
أمثلة لثوابت الألتواء لبض الأشكال الهندسية
دائرة
قطع ناقص
مربع
مستطيل
| a/b | |
|---|---|
| 1.0 | 0.141 |
| 1.5 | 0.196 |
| 2.0 | 0.229 |
| 2.5 | 0.249 |
| 3.0 | 0.263 |
| 4.0 | 0.281 |
| 5.0 | 0.291 |
| 6.0 | 0.299 |
| 10.0 | 0.312 |
| 0.333 |
[6] وبالتالي يمن استخدام هذة المعادلة بنسبة خطأ لا تزيد عن 4%
أنبوب رفيعة مفتوحة
مراجع
- ^ Archie Higdon et al. "Mechanics of Materials, 4th edition".
- ^ "Area Moment of Inertia." From MathWorld--A Wolfram Web Resource. http://mathworld.wolfram.com/AreaMomentofInertia.html نسخة محفوظة 18 مارس 2020 على موقع واي باك مشين.
- ^ أ ب Roark's Formulas for stress & Strain, 7th Edition, Warren C. Young & Richard G. Budynas
- ^ Continuum Mechanics, Fridtjov Irjens, Springer 2008, p238, ISBN 978-3-540-74297-5
- ^ Torsion Equations, Roy Beardmore, http://www.roymech.co.uk/Useful_Tables/Torsion/Torsion.html نسخة محفوظة 18 أبريل 2017 على موقع واي باك مشين.
- ^ Advanced Strength and Applied Elasticity, Ugural & Fenster, Elsevier, ISBN 0-444-00160-3
- ^ Advanced Mechanics of Materials, Boresi, John Wiley & Sons, ISBN 0-471-55157-0
| ثابت الالتواء في المشاريع الشقيقة: | |