سرعة مدارية

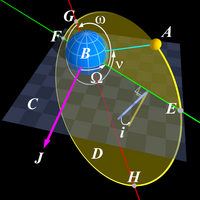
السرعة المدارية لأي جرم فلكي سواء كان كوكبا أوقمرا طبيعيا أوقمرا اصطناعيا أومتعددا هي سرعة حركته أثناء سيره في المدار.وتزداد السرعة المدارية كلما قرب الساتل من الجسم الذي يدور حوله.وتنخفض بابتعاده عن مركز الدوران. فالقمر الاصطناعي الذي يدور في المدار الأرضي المنخفض تكون سرعته المدارية أعلى من سرعة القمر الاصطناعي الذي يدور في المدار الأرضي المتوسط. تكون السرعة المدارية ثابتة عندما يكون المدار تام الاستدارة (على هيئة دائرة منتظمة)، أما المدارات ذات الشذوذ المداري فإن السرعة المدارية تختلف مع الزمن لذا يلجأ إلى حساب متوسط السرعة المدارية.

حساب السرعة المدارية

يعتمد حساب السرعة المدارية على معرفة نصف القطر من الساتل إلى مركز الدوران وكذلك على كتلة الجرم السماوي الذي يدور حوله الساتل إضافة إلى كتلة الساتل. ومضروب كتلة الجرم السماوي بثابت الجاذبية يساوي معامل الجذب المعياري.

$\mu =GM$

حيث:

$\mu$ معامل الجذب المعياري.

$G$ ثابت الجاذبية وقدره $G=6.67428\times 10^{-11}{\text{m}}^3{\text{kg}}^{-1}{\text{s}}^{-2}=6.67428\times 10^{-11}\mathrm{N}\mathrm{(}\mathrm{m}/\mathrm{k}\mathrm{g}{\mathrm{)}}^{\mathrm{2}}$

$M$ كتلة الجرم السماوي الذي يلتف الساتل حوله.

وبذلك يكون متوسط السرعة المدارية لساتل ما.

$v_o\approx \sqrt{\frac{\mu }{r}}$

حيث:

$v_o$ هي متوسط السرعة المدارية.

$r$ نصف القطر.

تعتبر المعادلة أعلاه صالحة للتطبيق إذا كانت كتلة الساتل صغيرة مقارنة بكتلة الجرم السماوي أي أنه بالمقدور تجاهلها.أما إذا كانت الكتلة كبيرة ولا يمكن تجاهلها كما في حالة النجم المضاعف فتحسب السرعة المدارية المتوسطة حسب الآتي:

$v_o\approx \sqrt{\frac{m_2^{2}G}{(m_1+m_2)r}}$

حيث:

$r$ نصف القطر وتمثل البعد بين مركزي ثقل الكتلتين.

$m_1$ كتلة الساتل الذي نريد حساب سرعته المدارية.

$m_2$ كتلة الجرم السماوي.

معادلة أخرى

ويمكن كذلك عند معرفة فترة الدوران ونصف المحور الأكبر لساتل ما معرفة سرعته المدارية بالمعادلة التالية المحورة من المعادلة أعلاه:

$v_o\approx \frac{2\pi a}{T}$

$v_o\approx \sqrt{\frac{\mu }{a}}$

حيث:

$T$ فترة الدوران.

$a$ نصف المحور الأكبر.