|
تضامنًا مع حق الشعب الفلسطيني |
ملف:Liquid Crystal based Spatial Light Modulator.gif
Liquid_Crystal_based_Spatial_Light_Modulator.gif (360 × 263 بكسل حجم الملف: 947 كيلوبايت، نوع MIME: image/gif، ملفوف، 80 إطارا)
| هذا ملف من ويكيميديا كومنز. معلومات من صفحة وصفه مبينة في الأسفل. كومنز مستودع ملفات ميديا ذو رخصة حرة. |
ملخص
| الوصفLiquid Crystal based Spatial Light Modulator.gif |
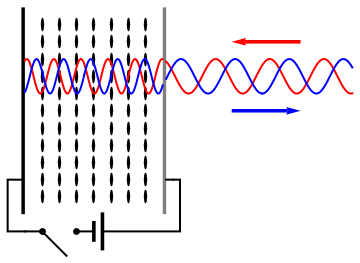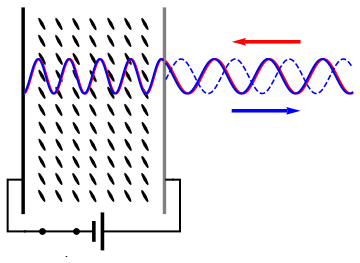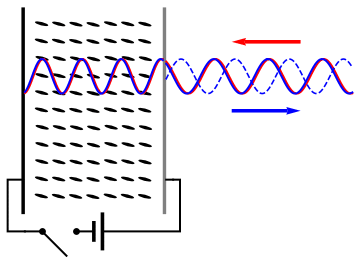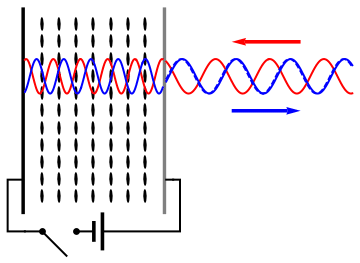
English: As (nematic) liquid crystals are birifrangent and their orientation can be changed applying an electric field, it is possible to change the refractive index seen by an incident wave applying a voltage to a liquid crystal cell and thus control the phase retardation of the reflected wave. |
| التاريخ | |
| المصدر | https://twitter.com/j_bertolotti/status/1144556106192183296 |
| المؤلف | Jacopo Bertolotti |
| الترخيص (إعادة استخدام هذا الملف) |
https://twitter.com/j_bertolotti/status/1030470604418428929 |
Mathematica 11.0 code
k1 = 2;
k2 = 4;
p1 = Table[
Show[
Graphics[{Polygon[{{-4.2, -6}, {-4, -6}, {-4, 6}, {-4.2, 6}}], Gray, Polygon[{{4.2, -6}, {4, -6}, {4, 6}, {4.2, 6}}], Black, Thick, Line[{{-4.1, -4}, {-5, -4}, {-5, -7}, {-3, -7}}], Disk[{-3, -7}, 0.2], Disk[{-1, -7}, 0.2], Line[{{-1, -7}, {0, -7}}], Line[{{0.5, -7}, {5, -7}, {5, -4}, {4.2, -4}}], Line[{{-3, -7}, {-3 + 2/Sqrt[2], -7 - 2/Sqrt[2]}}], Thickness[0.01], Line[{{0, -7.5}, {0, -6.5}}],
Line[{{0.5, -8}, {0.5, -6}}], Table[Rotate[Disk[{x, y}, {0.1, 0.4}], 0], {x, -3, 3, 1}, {y, -5, 5, 1}], Red, Arrow[{{12, 4}, {8, 4}}], Blue, Arrow[{{8, 0}, {12, 0}}] }],
Plot[Sin[k1 x] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}], Plot[Sin[k2 x + 4 (k1 - k2)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + k2 (4 + x)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}],
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2 + k1 x + 4 (k2 - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
]
, {\[Phi], 2 \[Pi], 0, -0.4}];
k1 = 2;
k2 = 4;
k2old = 4;
knew = 2.5;
p2 = Table[
k2 = \[Phi]/(2 \[Pi]) knew + (1 - \[Phi]/(2 \[Pi])) k2old;
Show[
Graphics[{Polygon[{{-4.2, -6}, {-4, -6}, {-4, 6}, {-4.2, 6}}], Gray, Polygon[{{4.2, -6}, {4, -6}, {4, 6}, {4.2, 6}}], Black, Thick, Line[{{-4.1, -4}, {-5, -4}, {-5, -7}, {-3, -7}}], Disk[{-3, -7}, 0.2], Disk[{-1, -7}, 0.2], Line[{{-1, -7}, {0, -7}}], Line[{{0.5, -7}, {5, -7}, {5, -4}, {4.2, -4}}], Line[{{-3, -7}, {-1, -7}}], Thickness[0.01], Line[{{0, -7.5}, {0, -6.5}}], Line[{{0.5, -8}, {0.5, -6}}]
, Table[Rotate[Disk[{x, y}, {0.1, 0.4}], \[Phi]/4], {x, -3, 3, 1}, {y, -5, 5, 1}], Red, Arrow[{{12, 4}, {8, 4}}], Blue, Arrow[{{8, 0}, {12, 0}}] }],
Plot[Sin[k1 x] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}], Plot[Sin[k2 x + 4 (k1 - k2)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + k2 (4 + x)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}],
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2 + k1 x + 4 (k2 - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2old + k1 x + 4 (k2old - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Dashed}]
]
, {\[Phi], 0, 2 \[Pi], 0.2}];
k1 = 2;
k2 = 4;
k2old = 4;
knew = 2.5;
p3 = Table[
k2 = \[Phi]/(2 \[Pi]) knew + (1 - \[Phi]/(2 \[Pi])) k2old;
Show[
Graphics[{Polygon[{{-4.2, -6}, {-4, -6}, {-4, 6}, {-4.2, 6}}], Gray, Polygon[{{4.2, -6}, {4, -6}, {4, 6}, {4.2, 6}}], Black, Thick, Line[{{-4.1, -4}, {-5, -4}, {-5, -7}, {-3, -7}}], Disk[{-3, -7}, 0.2], Disk[{-1, -7}, 0.2], Line[{{-1, -7}, {0, -7}}], Line[{{0.5, -7}, {5, -7}, {5, -4}, {4.2, -4}}], Line[{{-3, -7}, {-3 + 2/Sqrt[2], -7 - 2/Sqrt[2]}}], Thickness[0.01], Line[{{0, -7.5}, {0, -6.5}}],
Line[{{0.5, -8}, {0.5, -6}}], Table[Rotate[Disk[{x, y}, {0.1, 0.4}], \[Phi]/4], {x, -3, 3, 1}, {y, -5, 5, 1}], Red, Arrow[{{12, 4}, {8, 4}}], Blue, Arrow[{{8, 0}, {12, 0}}] }],
Plot[Sin[k1 x] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}], Plot[Sin[k2 x + 4 (k1 - k2)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Red, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + k2 (4 + x)] + 2, {x, -4, 4}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2 + k1 x + 4 (k2 - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Thick}]
,
Plot[-Sin[32 - 4 k1 + \[Pi] + 4 k2old + k1 x + 4 (k2old - k1)] + 2, {x, 4.2, 15}, Axes -> False, PlotRange -> All, PlotStyle -> {Blue, Dashed}]
]
, {\[Phi], 2 \[Pi], 0, -0.2}];
ListAnimate[Join[p1, p2, p3]]
ترخيص
| هذا الملف متوفر تحت ترخيص المشاع الإبداعي CC0 1.0 الحقوق العامة. | |
| لقد وَضَعَ صاحب حقوق التَّأليف والنَّشر هذا العملَ في النَّطاق العامّ من خلال تنازُلِه عن حقوق العمل كُلِّها في أنحاء العالم جميعها تحت قانون حقوق التَّأليف والنَّشر، ويشمل ذلك الحقوق المُتَّصِلة بها والمُجاورة لها برمتها بما يتوافق مع ما يُحدده القانون. يمكنك نسخ وتعديل وتوزيع وإعادة إِنتاج العمل، بما في ذلك لأغراضٍ تجاريَّةٍ، دون حاجةٍ لطلب مُوافَقة صاحب حقوق العمل.
http://creativecommons.org/publicdomain/zero/1.0/deed.enCC0Creative Commons Zero, Public Domain Dedicationfalsefalse |
الشروحات
العناصر المصورة في هذا الملف
يُصوِّر
قيمة ما بدون عنصر ويكي بيانات
٢٨ يونيو 2019
image/gif
تاريخ الملف
اضغط على زمن/تاريخ لرؤية الملف كما بدا في هذا الزمن.
| زمن/تاريخ | صورة مصغرة | الأبعاد | مستخدم | تعليق | |
|---|---|---|---|---|---|
| حالي | 17:00، 28 يونيو 2019 |  | 360 × 263 (947 كيلوبايت) | commonswiki>Berto | User created page with UploadWizard |
استخدام الملف
ال1 ملف التالي مكررات لهذا الملف (المزيد من التفاصيل):
- ملف:Liquid Crystal based Spatial Light Modulator.gif من ويكيميديا كومنز
الصفحة التالية تستخدم هذا الملف:
بيانات وصفية
هذا الملف يحتوي على معلومات إضافية، غالبا ما تكون أضيفت من قبل الكاميرا الرقمية أو الماسح الضوئي المستخدم في إنشاء الملف.
إذا كان الملف قد عدل عن حالته الأصلية، فبعض التفاصيل قد لا تعبر عن الملف المعدل.
| تعليق ملف GIF | Created with the Wolfram Language : www.wolfram.com |
|---|