قائمة عزم القصور الذاتي

فيما يلي جدولا بعزم القصور الذاتي لبعض الاشكال الشهيرة

الوصف	الشكل	عزم القصور الذاتي	تعليق
قشرة اسطوانية بنصف قطر r وكتلة m		$I = m r^{2}$	بفرض ان سمكا القشرة مهمل r₁=r₂.
انبوبة مفتوحة الطرفين سميكة بنصف قطر داخلي r₁, نصف قطر خارجي r₂, طول h و كتلة m		$I_{z} = \frac{1}{2} m ({r_{1}}^{2} + {r_{2}}^{2})$ $I_{x} = I_{y} = \frac{1}{12} m [3 ({r_{2}}^{2} + {r_{1}}^{2}) + h^{2}]$ أو عند تعريف سماكة عمودية t_n = t/r وبجعل r = r₂, then $I_{z} = m r^{2} (1 - t_{n} + \frac{1}{2} t_{n}^{2})$	لكثافة ρ ونفس التحليل الهندسي $I_{z} = \frac{1}{2} π ρ h ({r_{2}}^{4} - {r_{1}}^{4})$
اسطوانة مصمتة r, ارتفاعها h وكتلة m		$I_{z} = \frac{m r^{2}}{2}$ $I_{x} = I_{y} = \frac{1}{12} m (3 r^{2} + h^{2})$	هذه حالة خاصة من الجسم السابق لـ r₁=0.
قرص جاسئ بنصف قطر r وكتلة m		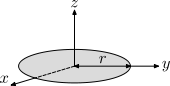$I_{z} = \frac{m r^{2}}{2}$ $I_{x} = I_{y} = \frac{m r^{2}}{4}$	هذه حالة خاصة من الجسم السابق لـ h=0.
حلقة نحيفة بنصف قطر r وكتلة m		$I_{z} = m r^{2}$ $I_{x} = I_{y} = \frac{m r^{2}}{2}$	هذه حالة خاصة من التورس لـb=0. (انظر اسفل.)
كرة مصمتة بنصف قطر r وكتلة m		$I = \frac{2 m r^{2}}{5}$	يمكن بناء الكرة من مجموعة قطع دائرية من 0 إلى r.
كرة محفورة بنصف قطر r وكتلة m		$I = \frac{2 m r^{2}}{3}$	.
كروي مفلطح الاعظمي a, الاصغر b وكتلة m	عرض الصورة بك	$I = \frac{2 m b^{2}}{3}$	—
عمودي قطع مخروطي بنصف قطر r, ارتفاع h وكتلة m		$I_{z} = \frac{3}{10} m r^{2}$ $I_{x} = I_{y} = \frac{3}{5} m (\frac{r^{2}}{4} + h^{2})$	—
مكعب مصمت بارتفاع h, width w, وعمق d, وكتلة m		$I_{h} = \frac{1}{12} m (w^{2} + d^{2})$ $I_{w} = \frac{1}{12} m (h^{2} + d^{2})$ $I_{d} = \frac{1}{12} m (h^{2} + w^{2})$	$s$ , $I_{C M} = \frac{m s^{2}}{6}$ .
مستوى نحيف مستطيل بارتفاع h وعرضه wوكتلة m		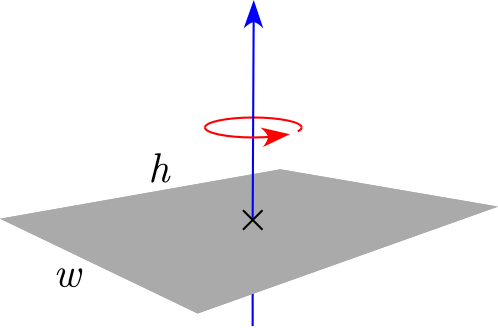$I_{c} = \frac{m (h^{2} + w^{2})}{12}$	—
مستوى مستطيل نحيف بارتفاع h وعرض w وكتلة m (محور الدوران على نهاية القطعة)		$I_{e} = \frac{m h^{2}}{3} + \frac{m w^{2}}{12}$	—
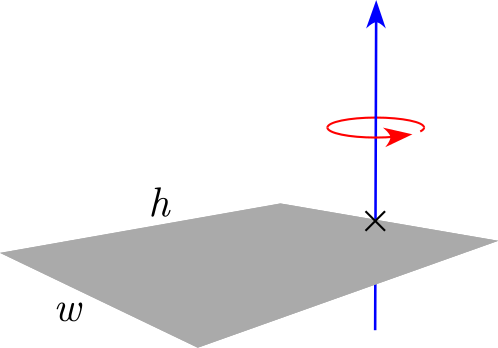قضيب بطول L وكتلة m		$I_{c e n t e r} = \frac{m L^{2}}{12}$
قضيببطول L وكتلة m (محور الدوران على طرف القضيب)		$I_{e n d} = \frac{m L^{2}}{3}$
تورس انبوب بنصف قطر a, نصف قطر مقطعي b وكتلة m.		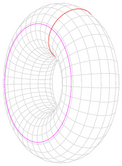حول قطر: $\frac{1}{8} (4 a^{2} + 5 b^{2}) m$ حول المحور العمودي: $(a^{2} + \frac{3}{4} b^{2}) m$	—
مستوى مضلع بؤرته ${\vec{P}}_{1}$ , ${\vec{P}}_{2}$ , ${\vec{P}}_{3}$ , ..., ${\vec{P}}_{N}$ وكتلة $m$ موزعة بانتظام من الداخل, وتدور حول المحور عموديا على المستوى مارة خلال نقطة الاصل.		$I = \frac{m}{6} \frac{\sum_{n = 1}^{N} \| {\vec{P}}_{n + 1} \times {\vec{P}}_{n} \| ({\vec{P}}_{n + 1}^{2} + {\vec{P}}_{n + 1} \cdot {\vec{P}}_{n} + {\vec{P}}_{n}^{2})}{\sum_{n = 1}^{N} \| {\vec{P}}_{n + 1} \times {\vec{P}}_{n} \|}$	—

بوابة الفيزياء

هذه بذرة مقالة عن الفيزياء أو موضوع فيزيائي بحاجة للتوسيع. فضلًا شارك في تحريرها.