فتل

إن عملية الحدرجة أو الفتل أو اللي (بالإنجليزية: Torsion)‏ هي واحدة من الجهود الرئيسية التي يمكن أن يخضع لها جسم مرن ما، إلى جانب الشد ، الضغط ، إنثناء و القصّ. الحـَـدْرَجـَـة تصف وتميـّـز التواء جسم مرن عندما يقع تحت تأثير عزم دوران الحدرجة.

عارضة دائرية تتعرض لعزم دوران الحـَـدْرَجـَـة من جهتين

فتل أو لي عمود ذو مقطع مربع.

عارضة أسطوانية مكبوسة في جدار من جهة وتتعرض لعزم دوران الحـَـدْرَجـَـة من جهة أخرى

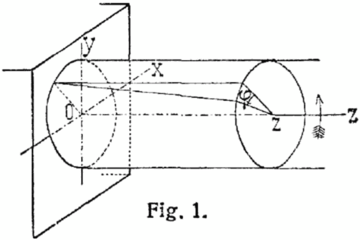
ويتحقق إيجاد الإجهاد الناتج عن ذاك - وهو إجهاد القصّ - كالآتي:

الصنف : عارضة أسطوانية بمساحة ثابتة لأي ّ مقطع متعامد للمحور $z$ :

الأوضاع الجيومترية :

$\gamma (r)l=\phi r$

فيها :

$\gamma (r)$ : زاوية على السطح الأسطواني من المقطع، وهي دالـّـة بحجـّـة $r$

$r$ : نصف قطر العارضة الأسطوانية أو كعبرة العارضة الأسطوانية

$[r]=1m$

$l$ : طول الاسطوانة

$[l]=1m$

$\phi$ : زاوية الالتواء

إجهاد القص :

$\tau (r)=G\cdot \gamma (r)=G\phi \cdot \frac{r}{l}$

فيها :

$\tau (r)$ : إجهاد القصّ، وهذا يعتبر دالـّـة بحجـّـة $r$

$[\tau ]=1N{m}^{-2}$

$G$ : معامل القصّ

$[G]=1N{m}^{-2}$

والكمـّـيـّـات الأخرى هي مذكورة سابقاً.

أمـّـا عزم دوران الحدرجة فهو يـُـكتسـَـب من توازن الأعزام :

${\int }_{A}r\cdot \tau (r)dA-T_t=0$

فيها :

$T_t$ : عزم دوران الحدرجة، موجـّـه في المثل المختار تجاه المحور $z$

$[T_t]=1Nm$

$A$ : مساحة مقطع العمود - بمقطع ٍ الذي يأتي في المثل المختار هنا متعامد للمحور $z$

$[A]=1m^2$

وذلك يؤدّي إلى :

$G\cdot \frac{\phi }{l}{\int }_A{r}^{2}dA-T_t=0$

فيها :

$I_p={\int }_A{r}^{2}dA$ : عزم مساحي قطبي للعطالة (polar area moment of inertia)

$[I_p]=1m^4$

المعادلة الأخيرة تؤدّي مع معادلة أجهاد القصّ إلى :

$\frac{\phi }{l}=\frac{T_t}{G{I}_p}$

وذلك يسمح الحصول على زاوية الاِلتواء على الفور :

$\phi =\frac{T_{t}l}{G{I}_p}$

و يتمّ إيجاد إجهاد القصّ بمعادلة الإجهاد فوق :

$\tau (r)=\frac{T_t}{I_p}\cdot r$

انظر أيضاً

• جسم صلب
• مرونة
• عزم التواء