صورة الطور

صورة الطور هي تمثيل هندسي لمسارات النظام الديناميكي في مستوى الطور. يتم تمثيل كل مجموعة من الشروط الأولية بمنحنى أو نقطة مختلفة.

الطاقة الكامنة وصورة الطور لبندول بسيط . لاحظ أن المحور س، كونه زاويًا، يلتف على نفسه بعد كل 2π راديان.

توضيح لكيفية بناء صورة طورية لحركة بندول بسيط.

صورة طور لمعادلة فان دير بول ، $\frac{d^{2}y}{d{t}^2}+\mu (y^2-1)\frac{dy}{dt}+y=0$ .

تعد صور الطور أداة لا تقدر بثمن في دراسة الأنظمة الديناميكية. وهي تتكون من رسم المسارات المحتملة للمتحولات في فضاء الحالة. تكشف صورة الطور عن معلومات مثل ما إذا كان الجاذب أو الطارد أو دورة الحد موجودًا لقيمة المعلمة المختارة. يمثل الجاذب نقطة مستقرة تسمى أيضًا «بالوعة». ويعتبر الطارد نقطة غير مستقرة، والتي تُعرف أيضًا باسم «المصدر». إن مفهوم التكافؤ الطوبولوجي مهم في تصنيف سلوك الأنظمة من خلال تحديد متى تمثل صورتين مختلفتين للطور نفس السلوك الديناميكي النوعي.

يصور رسم بياني طوري لنظام ديناميكي مسارات النظام (الأسهم) والحالات الثابتة المستقرة (النقاط) والحالات الثابتة غير المستقرة (الدوائر) في فضاء الحالة. إن المحاور في صورة الطور هي متغيرات الحالة.

أمثلة

• بندول بسيط، انظر الصورة (يمين).
• مذبذب توافقي بسيط حيث تتكون صورة الطور من علامات الحذف المتمركزة في الأصل، وهي نقطة ثابتة.
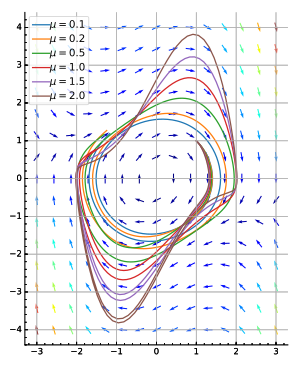
• مذبذب فان دير بول انظر الصورة (أسفل اليمين).
• مستوى المعلمة (المستوى ج) ومجموعة ماندلبروت

صور الطور لتصور سلوك نظم المعادلات التفاضلية العادية

تمثل الصورة الطورية السلوك الاتجاهي لنظام ODEs. يمكن أن تشير صورة الطور إلى استقرار النظام كما يلي.

الاستقرار

غير مستقر	تميل معظم حلول النظام نحو ∞ بمرور الوقت
مستقر بشكل تقاربي	تميل جميع حلول النظام إلى 0 بمرور الوقت
مستقر محايد	لا يميل أي من حلول النظام نحو ∞ بمرور الوقت، ولكن معظم الحلول لا تميل إلى الصفر أيضًا

انظر أيضًا

• مساحة المرحلة
• مستوى الطور

روابط خارجية

• صور المرحلة الخطية ، MIT Mathlet.