دالتا الجزء الصحيح والمتمم الصحيح الأعلى

في الرياضيات وفي علم الحاسوب، دالتا الجزء الصحيح والمتمم الصحيح الأعلى، (بالإنجليزية: Floor and ceiling functions)‏ تربطا عددا حقيقيا ما بأكبر عدد صحيح سابق أو أصغر عدد صحيح تابع على التوالي، حيث:

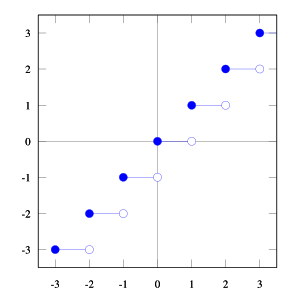
• الجزء الصحيح أو المتمم الصحيح الأسفل لعدد حقيقي ما x هو أكبر عدد صحيح ليس أكبر من x. فصحيح العدد 2.6 هو 2، أي أكبر عدد صحيح ليس أكبر من 2.6 .
• بينما السقف أو المتمم الصحيح الأعلى لعدد حقيقي x فهو أصغر عدد صحيح ولكن ليس أصغر من x. فسقف العدد 2.15 هو 3، أي أصغر عدد صحيح ليس أصغر من 2.15.

دالة الجزء الصحيح

دالة السقف

الرموز المستعملة

استعمل كارل فريدريش غاوس في عام 1808 رمز المعقوفتين [x] للدلالة على الجزء الصحيح في برهانه الثالث لمبرهنة التربيعية التبادلية. بقي هذا الرمز هو المرجع حتى أدخل كينيث ايفرسون في عام 1962 الكلمتين الإنجليزيتين Floor و Ceiling مع الرمزين الدالين عليهما $\rfloor$x$\lfloor$ و $\rceil$x$\lceil$ في كتاب له تحت عنوان لغة البرمجة (A Programming Language).

أمثلة

قيمة ما ل x	الجزء الصحيح $\lfloor x\rfloor$	السقف $\lceil x\rceil$	الجزء الكسري $\{x\}$
12/5 = 2.4	2	3	2/5 = 0.4
2.7	2	3	0.7
$-2.7$	$-3$	$-2$	0.3
$-2$	$-2$	$-2$	0

تطبيقات

ثابتة أويلر

هناك صيغ رياضياتية تتعلق بثابتة أويلر-ماسكيروني γ = 0.57721 56649 ... تحتوي على دالتي الجزء الصحيح والسقف. على سبيل المثال

$\gamma =\underset{1}{\overset{\mathrm{\infty }}{\int }}(\frac{1}{\lfloor x\rfloor }-\frac{1}{x})dx,$

$\gamma =\underset{n\to \mathrm{\infty }}{lim}\frac{1}{n}\sum _{k=1}^n(\lceil \frac{n}{k}\rceil -\frac{n}{k}),$

و

$\gamma =\sum _{k=2}^{\mathrm{\infty }}(-1{)}^k\frac{\lfloor {\log }_{2}k\rfloor }{k}=\frac{1}{2}-\frac{1}{3}+2(\frac{1}{4}-\frac{1}{5}+\frac{1}{6}-\frac{1}{7})+3(\frac{1}{8}-\dots -\frac{1}{15})+\dots$

معضلات حلت

طرح رامانجن المعضلة التالية لجريدة للجمعية الرياضياتية الهندية.

إذا كان n عددا صحيحا موجبا، أثبت أن:

(i)     $\lfloor \frac{n}{3}\rfloor +\lfloor \frac{n+2}{6}\rfloor +\lfloor \frac{n+4}{6}\rfloor =\lfloor \frac{n}{2}\rfloor +\lfloor \frac{n+3}{6}\rfloor ,$

(ii)     $\lfloor \frac{1}{2}+\sqrt{n+\frac{1}{2}}\rfloor =\lfloor \frac{1}{2}+\sqrt{n+\frac{1}{4}}\rfloor ,$

(iii)     $\lfloor \sqrt{n}+\sqrt{n+1}\rfloor =\lfloor \sqrt{4n+2}\rfloor .$

معضلات لم تحل بعد

انظر إلى معضلة ويرينغ.

وصلات خارجية

• شرح بالفيديو لدالة الجزء الصحيح