|
تضامنًا مع حق الشعب الفلسطيني |
معضلة يوم الميلاد
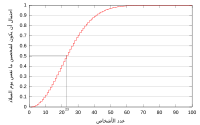
في نظرية الاحتمال، معضلة يوم الميلاد أو مفارقة يوم الميلاد[1][2] تتعلق باحتمال أن يكون لشخصين اختيرا بصفة عشوائية داخل مجموعة مكونة من عدد n معين من الأشخاص، نفس يوم الميلاد خلال السنة (بما في ذلك إن ولدا في عامين مختلفين ولكنهما ولدا في نفس اليوم من السنة. الفاتح من مايو مثلاً).[3]
مفهومها
تشير هذه النظرية إلى الاحتمال الذي يتحقق من احتمال وجود اثنين على الأقل من الأشخاص الذين يحتفلون بعيد ميلادهم في نفس اليوم من العام الواحد، عندما يتم اختيار مجموعة عشوائية من الأشخاص.
عندما يتم اختيار مجموعة صغيرة من الأشخاص، يبدو من المنطقي أن فرصة وجود شخصين يحتفلان بعيد ميلادهم في نفس اليوم تكون صغيرة جدًا. ومع ذلك ، فإن نظرية مفارقة عيد الميلاد تظهر أن هذا الاعتقاد خاطئ ويتنافى مع الحقائق الإحصائية.
يتم تفسير هذا النظرية من خلال النظر إلى الأمر بشكل أكثر تفصيلا. في مجموعة صغيرة من 23 شخصًا، فإن الاحتمال الذي يحدث فيه أن يكون لديهم اثنان على الأقل يحتفلون بعيد ميلادهم في نفس اليوم هو 50٪ تقريبًا. يمكن أن يكون هذا الأمر مفاجئًا لبعض الأشخاص، ولكن عندما يتم زيادة عدد الأشخاص في المجموعة، يصبح الاحتمال أعلى.
يمكن أن نرى هذا على سبيل المثال، إذا كان لدينا مجموعة من 50 شخصًا، فإن الاحتمال الذي يحدث فيه أن يوجد اثنين على الأقل يحتفلون بعيد ميلادهم في نفس اليوم هو 97٪. وعندما يصل العدد إلى 70، يكون هناك احتمال بلغ 99.9٪ أن يكون لدينا شخصان على الأقل يحتفلان بعيد ميلادهم في نفس اليوم.
على الرغم من أن نظرية مفارقة عيد الميلاد لا تنطبق دائمًا على كل السيناريوهات، إلا أنها توضح أهمية دراسة الاحتمالات والتوقعات في العديد من المواقف الحياتية. ويمكن لهذه النظرية أن تستخدم في مجالات مختلفة مثل تحليل البيانات والأمن السيبراني وغيرها من المجالات التي تعتمد على الحسابات الإحصائية.
الخاتمة
بشكل عام، فإن نظرية مفارقة عيد الميلاد تشير إلى مدى تعقيد الاحتمالات في الأحداث العشوائية وأهميتها في فهم البيانات واتخاذ القرارات المناسبة. ويمكن استخدام هذه النظرية في العديد من المجالات للحصول على نتائج أكثر دقة وفعالية.
مراجع
- ^ Check your intuition: The birthday problem - David Knuffke، مؤرشف من الأصل في 2022-12-30، اطلع عليه بتاريخ 2023-02-20
- ^ THOMAS H. CORMEN
CHARLES E. LEISERSON
RONALD L. RIVEST (2009). Introduction to Algorithms, third edition Computer science Online access with purchase: ebrary The MIT Press (بEnglish) (Third Edition ed.). MIT Press, 2009. Vol. Chapter 5. p. 130. ISBN:0262033844, 9780262033848.
{{استشهاد بكتاب}}:|طبعة=يحتوي على نص زائد (help), line feed character في|مؤلف=في مكان 17 (help), and تأكد من صحة|isbn=القيمة: حرف غير صالح (help) - ^ دبليو دبليو روس بول, 1960, Other Questions on Probability, in "Mathematical Recreations and Essays", Macmillan, New York, p 45.
| في كومنز صور وملفات عن: معضلة يوم الميلاد |