قانون هاجن-بوازوي

a) انبوب يجري فيه مائع جريان صفائحي. b) مقطع في الأنبوب يوضح توزيع سرعات الطبقلت المختلفة للمائع. طبقات المائع المجاورة للسطح الداخلي للأنبوب تكون سرعتها منخفضة عن تلك التي تجري في وسط الأنبوب. أطوال الأسهم تعطي مقادير السرعة.

قانون هاجن-بوازوي (بالإنجليزية: Hagen–Poiseuille law) هو قانون للعالمين «جوتهيلف هاجن» الألماني 1797–1884 و «جين بوازوي» الفرنسي 1797–1869)، يصف حركة جريان مائع (مثل الماء) في أنبوب. يعرف ما يسمى «حجم الجريان» $\dot{V}$ (أي الحجم V المتحرك في الثانية) في حالة جريان صفائحي لمائع نيوتن في أنبوب نصف قطره r وطولها l .

القانون

صيغة القانون كالآتي:

$\dot{V}=\frac{dV}{dt}=\frac{\pi \cdot r^4}{8\cdot \eta }\frac{\mathrm{\Delta }p}{l}=-\frac{\pi \cdot r^4}{8\cdot \eta }\frac{\partial p}{\partial z}$

حيث:

المتغير	معناه	بوحدات SI
$\dot{V}$	حجم الجريان	$\frac{{\mathrm{m}}^{\mathrm{3}}}{\mathrm{s}}$
$r$	نصف القطر الداخلي للأنبوب	m
$l$	طول الأنبوب	m
$\eta$	اللزوجة الحركية للمائع الجاري	Pa·s
$\mathrm{\Delta }p$	فرق الضغط بين أول الأنبوب وآخره	Pa
z	اتجاه الجريان

حيث وحدات SI (النظام الدولي للوحدات)، ومن ضمنها هنا متر، وثانية، باسكال (وحدة) .

نشأة اضطرابات (دوامات) أثناء جريان صفائحي لمائع

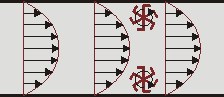
يصف هذا القانون توزيع السرعات لطبقات الماء الاسطوانية داخل الأنبوب على أساس معادلات نافير-ستوكس، أو يمكن استنتاجها أيضا من اللزوجة. هذا التوزيع يتبع شكل قطع مكافيء كما هو موضح في الشكل، حيث يعطي طول السهم سرعة طبقة المائع.

والخاصية الملفتة للنظهر هنا أن «حجم الجريان» يعمد على القوة 4 لنصف قطر الأنبوب. بالتالي تعتمد مقاومة الجريان في الأنبوب على نصف قطر الأنبوب، بمعنى أنه بتقليل نصف قطر الأنبوب إلى النصف يزيد مقاومة الجريان 16 مرة.

تطبيقات

في مجال انطباق القانون (جريان صفائحي غير مضطرب) في انبوب ذو مقطع دائري، فبتصغير نصف القطر بنسبة 10% تعمل على خفص انسياب المائع بنسبة $1-0,9^4=34\%$ . وفي حالة رغبتنا في زيادة جريان المائع إلى المقدار السابق قبل تصغير نصف قطر الأنبوب، فهذا يستلزم رفع فرق الضغط بنسبة 52%.

كما يستخدم قانون هاجن-بوازوي لاستنباط معادلات لنماذج تخص جريان مواد سائبة، مثل الماء والدقيق والرمل والخرسانة وغيرها.

أقرأ أيضاً

• جريان مضطرب
• جريان ستوكس
• طبقة حدية
• عدد ستروهال
• عدد رينولد
• شارع كارمان الدوامي
• جريان صفائحي